Dynamic boundary characteristics for truncated model of V-shaped orthogonally stiffened plates
-
摘要:目的
旨在研究截断模型与原模型动力边界等效问题，为开展船舶与海洋结构物动力特性研究打下基础。
方法采用有限元方法计算自由边界下V形板模型和一条边弹性支撑，另外三边自由边界下孤立板模型的固有频率与振型，将V形连接板模型固有频率及振型与孤立板模型进行对比，探究了板架截断模型动力边界等效规律。形形形
结果研究表明：随着附板厚度增加，V形连接板第(m, n)阶主板模态在沿附板耦合边方向的半波数m不变，垂直于附板耦合边方向的半波数n增加；随着附板长度增加，V形连接板第(m, n)阶主板模态在沿附板耦合边方向的半波数m不变，垂直于附板耦合边方向的半波数n减小；当V形板主板与附板耦合角度α介于40°与90°时，V形板附板相当于给主板提供了一个固支边界条件。
结论提出一个快速预报V形板部分模态固有频率的方法，对设计和评估船舶与海洋工程局部板架结构动力性能具有重要意义。形
Abstract:ObjectivesTo study the dynamic characteristics of local structures in naval architecture and ocean engineering, the dynamic boundary equivalence method between truncated model and original model should be explored.
MethodsThe finite element method is used to calculate the natural frequency and vibration mode of the V-shaped plate model and one-side elastic support under the free boundary. In addition, the natural frequency and vibration mode of the isolated plate model under the three-side free boundary are compared with the isolated plate model, and the equivalent law of the dynamic boundary of the truncated plate model is explored.
ResultsThe research shows that with the increase of the thickness of the attached plate, the half wave number m of the (m, n) order of V-shaped plates mode is constant along the coupled edge direction, and the half wave number n perpendicular to the coupled edge direction increases; With the increase of the length of the attached plate, the half wave number m of the (m, n) order of V-shaped plates mode is constant along the coupled edge direction, and the half wave number n perpendicular to the coupled edge direction of the attached plate decreases. When the coupling angle α between the main plate and the attached plate is between 40° and 90°, the attached plate of the V-shaped plate is equivalent to providing a fixed support boundary condition for the main plate.
ConclusionsA fast prediction method for the natural frequency corresponding to the partial modes of the V-shaped plate is proposed.
-
0. 引 言
在船舶与海洋结构物上大量使用连接板架单元形成的封闭或者半封闭空间，为人类开发和利用海洋资源提供稳定可靠的作业平台[1]，其动力性能直接影响船舶与海洋工程装备的作业性能和工作人员的作业安全[2]。在研究船舶与海洋结构物局部结构的动力特性时，通常需要对局部板架结构进行截断处理，将与之相连接的板架结构等效为合适的边界条件。研究原模型与边界等效后模型动力特性区别与联系，以及相关参数的影响对船舶与海洋工程装备动力性能评估与优化设计具有重要意义。船体结构由大量板梁构件组成，实际情况非常复杂，本文从船舶与海洋结构物中常见的、较为简单的V形板入手开展边界等效研究，为复杂结构动力边界等效问题研究提供理论基础与技术支撑。
国内外学者针对V形连接板架结构和L形这种特殊的V形连接板架结构开展了大量关于其动力特性、能量传递、动力响应和抗爆抗冲击性能等方面的研究工作。Xie等[3]研究了边界条件、耦合关系、耦合角度和结构尺寸等因素对L形板动力特性的影响。针对由多个L形结构组成的箱形结构，Chen等[4]研究了对称耦合、非对称耦合和激励等因素对其能量传递特性的影响。Zhang等[5]研究了谐波激励方向和板间耦合角度对耦合板动力响应的影响。Shao等[6]研究了V形板材料参数和耦合参数对功率流及其传递效率的影响。汤冬等[7]研究了耦合角度、板厚和阻尼损耗因子等参数对V形薄板的功率流透射损失的影响。Markose和Rao[8]研究了炸药量和V形板的夹角对其抗爆抗冲击性能的影响。
国内外学者开展了大量针对加筋板边界条件对其动力特性影响的研究工作。Wang等[9]研究了四边简支以及一对边简支、另一对边固支边界条件下矩形加筋板的自由振动问题。Du等[10]分析了经典边界条件和弹性边界条件下加筋板的自由振动和受迫振动响应。基于一阶剪切变形板理论，Shen等[11]和Qin等[12]采用无网格方法分别研究了经典边界条件下加筋板的受迫振动特性和固支边界条件下圆形加筋板的弯曲自由振动特性。Peng等[13]分析了边界条件对加筋板自由振动的影响。针对谐振器和加筋板耦合模型，Tian等[14]研究了简支边界条件下超材料加筋板的振动抑制问题。针对任意边界条件下复合材料加筋板的自由振动问题，Maji等[15]和Rajawat等[16]采用有限元法分别研究了边界条件对石墨烯增强复合材料加筋板和加筋层合板固有频率的影响。Gao等[17]采用半解析方法分析了一般弹性支撑边界条件下加筋板的自由振动响应，发现边界条件对加筋板的动力特性有显著影响。
通过对V形板动力特性研究和边界条件对加筋板动力特性影响研究相关文献的回顾和总结发现，国内外学者针对V形板的自由振动与强迫振动响应及其影响因素开展了大量研究工作，也有很多学者分析了边界条件对加筋板动力特性的影响。然而，将这两方面问题结合起来，开展截断模型与原模型动力边界等效问题的相关研究十分少见。本文以船舶与海洋结构物中V形连接板及其等效边界条件下的孤立板为研究对象，采用有限元方法计算自由边界条件下不同耦合角度、不同附板厚度、不同附板长度V形连接板的固有频率与振型，分析V形连接板参数对其动力特性的影响，同时计算一边弹性支撑、另外三边自由边界条件下孤立板的固有频率与振型，将原模型与边界等效模型的固有频率与振型进行对比，探究V形连接板动力特性与弹性支撑孤立板动力特性的等效规律。
1. V形连接板有限元模型与网格尺寸有效性分析
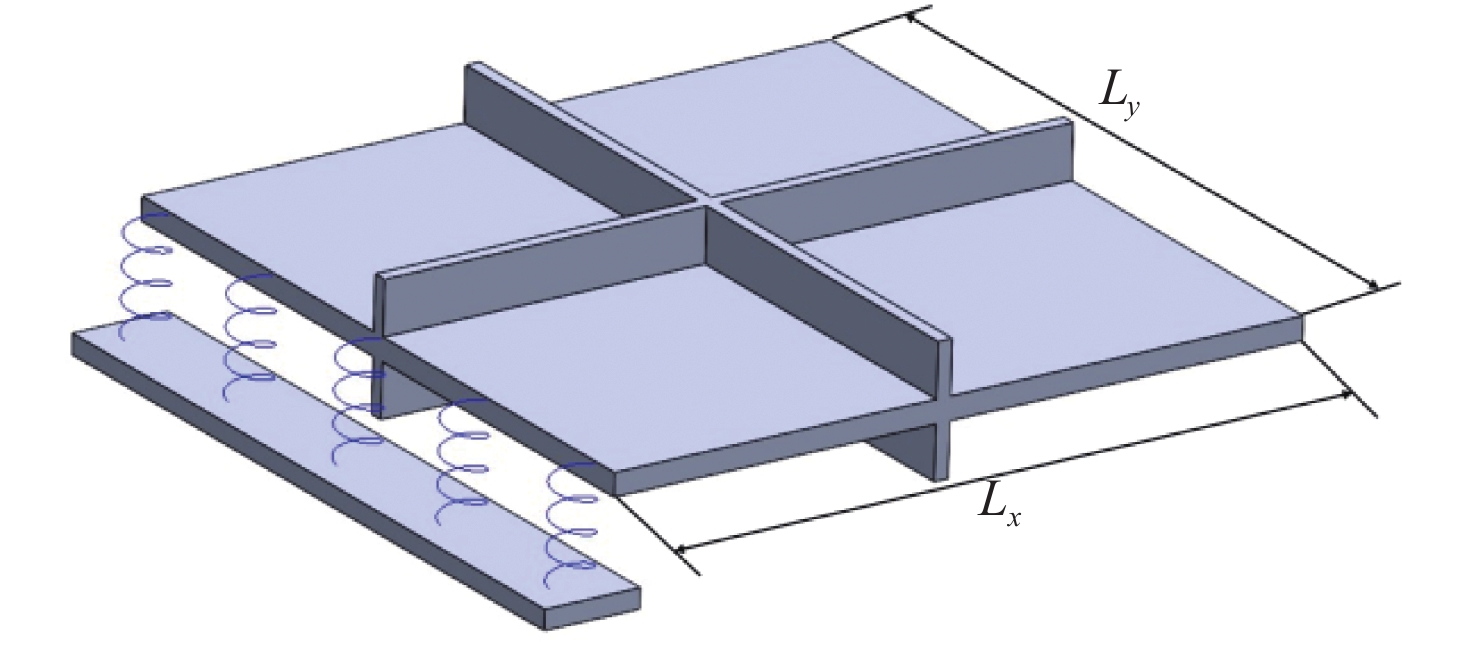
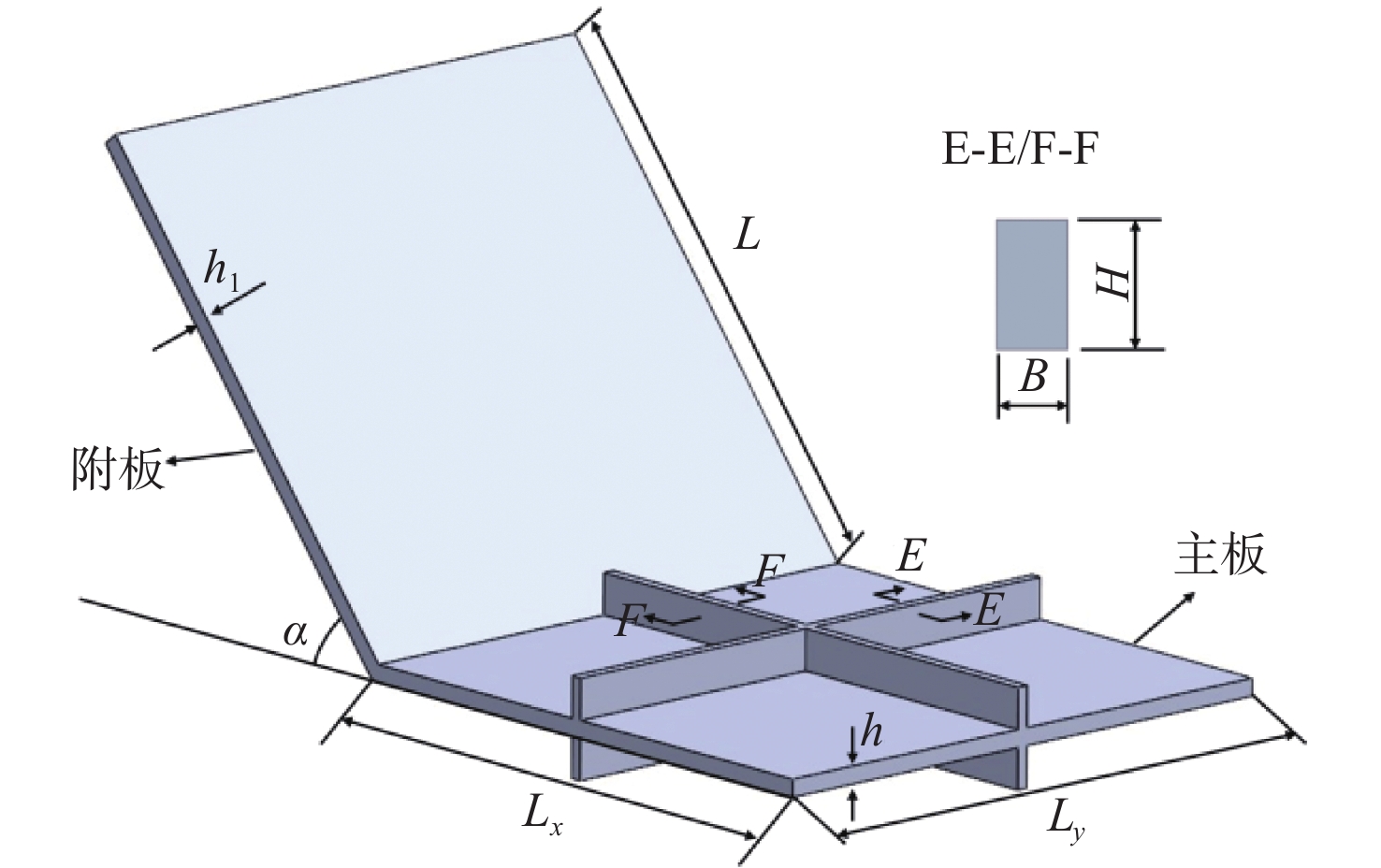
工程实践中常将2块板连接起来形成V形结构，例如船体因型线要求在船体舷侧外板的不同位置会与甲板板架呈现出不同角度V形空间板架结构，因此，分析夹角对V形连接板本征动力特性的影响具有重要的工程意义。如图1所示，V形连接板由主板、附板和主板上的加强筋组成。主板长度Lx与宽度Ly相等，厚度为h，附板宽度与主板宽度相同，附板长度和厚度分别为L和h1，加强筋截面为矩形，高度和宽度分别为H和B，V形连接板夹角的补角为α。
本文采用有限元法计算V形连接板固有频率与振型，有限元模型的网格尺寸会对计算结果准确性产生影响。一般而言，计算精度会随着网格减小而提高，但随之而来的是计算成本和计算时间的增加。在开展V形连接板动力特性分析前，需要确定合适的网格尺寸，在保证计算结果准确性的前提下有效降低计算成本、提高计算效率。
本文采用有限元软件ABAQUS计算如图1所示V形连接板模型在自由边界条件下的固有频率和振型，模型采用钢质材料，其材料属性与几何参数见表1。有限元模型的板采用四节点减缩积分单元（S4R），加强筋采用线性梁单元（B31）。主板沿宽度Ly方向上和长度Lx方向上的模态数分别用m和n来表示，不同网格尺寸计算得到的主板(m, n)阶模态固有频率及相邻网格尺寸下固有频率的最大差值（相邻网格尺寸同阶固有频率相差百分比的最大值）如表2所示。
表 1 V形连接板数值模型材料属性和几何参数Table 1. Material properties and geometric parameters of V-shaped plate参数 数值 弹性模量E/Pa 2.1×1011 密度ρ/(kg·m−3) 7 800 泊松比v 0.3 主板厚度h/m 0.01 主板长度Lx/m 1.00 主板宽度Ly/m 1.00 附板厚度h1/m 0.01 附板长度L/m 0.70 加强筋高度H/m 0.02 加强筋宽度B/m 0.01 V形板夹角的补角α/（°） 60 表 2 不同网格尺寸下V形连接板的固有频率及其最大差值Table 2. Natural frequencies and their maximum differences of V-shaped connecting plates under different grid sizes网格属性 不同阶数(m, n)的固有频率 最大差值/% 尺寸/m 网格数量 (1, 1) (2, 2) (3, 3) (4, 4) 0.010 17 924 127.07 341.98 625.64 1 042.46 — 0.009 22 516 127.04 341.89 625.36 1 041.82 0.061 0.008 28 360 127.02 341.81 625.14 1 041.31 0.049 0.007 36 427 127.00 341.73 624.94 1 040.83 0.046 0.006 49 933 126.98 341.66 624.74 1 040.42 0.041 0.005 71 422 126.95 341.59 624.57 1 040.03 0.036 0.004 110 299 126.94 341.54 624.43 1 039.71 0.032 0.003 197 003 126.93 341.50 624.32 1 039.51 0.019 0.002 433 856 126.92 341.47 624.27 1 039.34 0.019 由表2发现，当网格尺寸为0.005 m时，V形连接板固有频率已经收敛，此时网格数量为71 422，最大差值为0.036%，计算精度高，计算量适中，故本文有限元模型的网格尺寸选择为0.005 m。
为了验证建模方法的正确性和网格尺寸的合理性，建立文献[5]中的V形板模型进行计算，其中网格尺寸采用网格收敛性研究结果，即网格尺寸取为0.005 m。文献[5]中Lx=0.4 m，Ly=0.4 m，板厚h=0.003 m，材料弹性模量E=206 GPa，泊松比v=0.3，密度ρ=7 850 kg/m3，α=30°。计算结果如表3所示。
从表3可以看出，与文献[5]的固有频率结果相比，V形板的前5阶固有频率误差小于0.3%，由此说明本文所构建的V形板模型以及所选用的网格尺寸是合理的。
2. 耦合角度对V形连接板本征动力特性的影响
2.1 V形连接板耦合角度选取范围
V形连接板几何模型如图1所示，数值模型采用的除角度α外的所有材料参数与几何参数见表1。由于结构中常见板与板夹角为钝角，本文采用α作为分析参数，分别针对α为0°，3°，6°，9°，12°，15°，18°，20°，30°，40°，…，90°的V形连接板模型计算其固有频率与振型。
2.2 耦合角度对V形连接板本征动力特性的影响分析
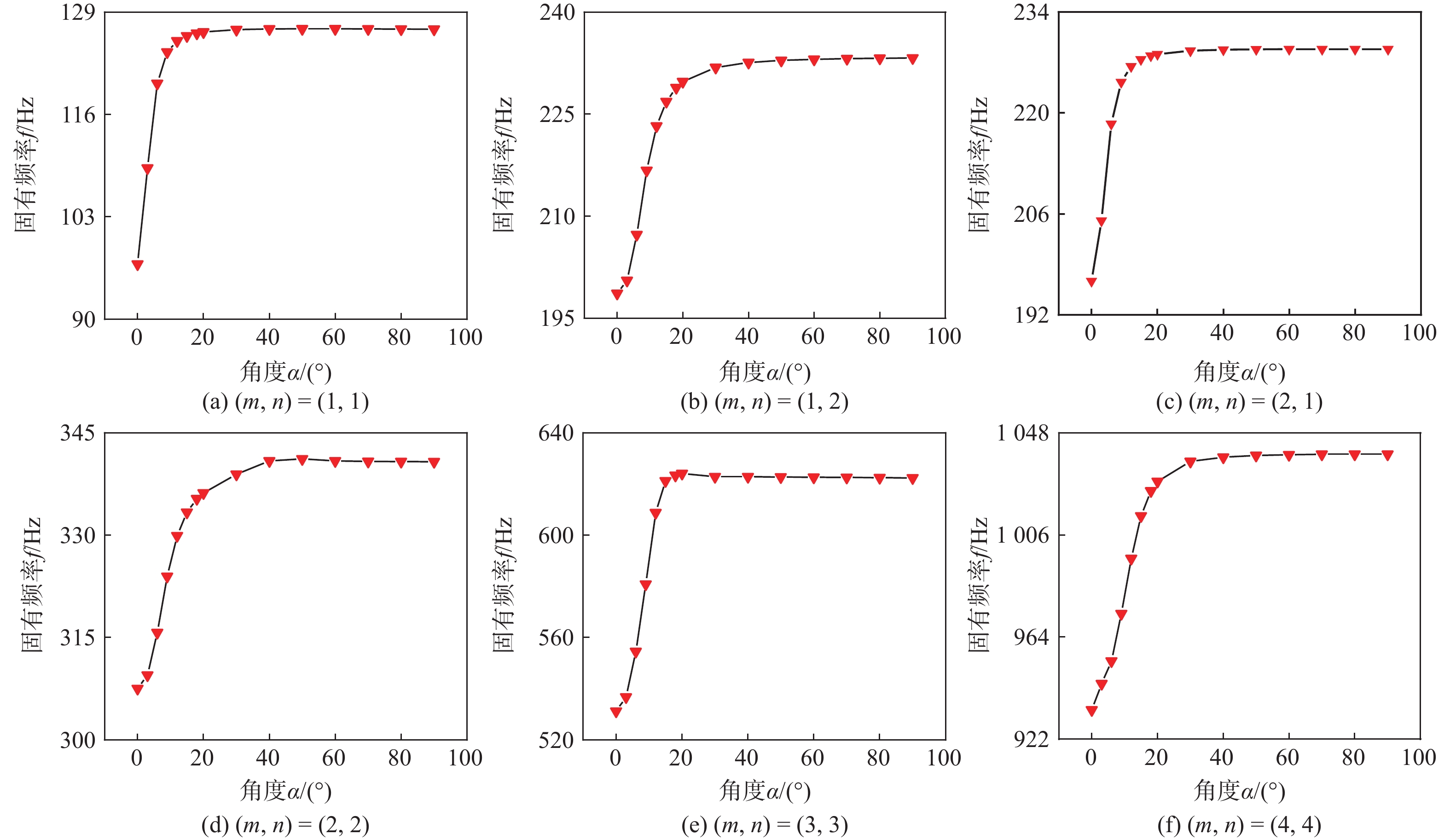
在分析夹角对V形连接板本征动力特性的影响时，选取主板(m, n)阶模态为研究对象，考察其在不同夹角时的固有频率，其中m, n分别为Ly和长Lx方向的模态数。不同角度α下V形连接板主板(m, n)阶模态固有频率及其随α的变化率κ1见表4。V形连接板固有频率随α的变化规律如图2所示，变化率κ1为相邻角度固有频率变化量绝对值与角度变化量绝对值的比值。
表 4 不同耦合角度α下V形连接板主板第(m, n)阶模态固有频率f及其变化率κ1Table 4. The (m, n)-order natural frequencies f and their variation rate κ1 of V-shaped plates under different coupling angles αα/(°) (1, 1) (1, 2) (2, 1) (2, 2) (3, 3) (4, 4) f/Hz κ1 f/Hz κ1 f/Hz κ1 f/Hz κ1 f/Hz κ1 f/Hz κ1 0 97.09 — 198.63 — 196.69 — 307.53 — 531.24 — 934.07 — 3 109.20 4.04 200.55 0.64 205.07 2.79 309.49 0.65 536.77 1.84 944.82 3.58 6 119.96 3.59 207.28 2.24 218.48 4.47 315.73 2.08 554.57 5.93 954.14 3.11 9 123.94 1.33 216.73 3.15 224.28 1.93 323.97 2.75 580.85 8.76 973.66 6.51 12 125.36 0.47 223.26 2.18 226.45 0.72 329.93 1.99 608.80 9.32 996.29 7.54 15 125.99 0.21 226.85 1.20 227.43 0.33 333.37 1.15 621.25 4.15 1 013.80 5.84 18 126.33 0.11 228.89 0.68 227.94 0.17 335.35 0.66 623.38 0.71 1 024.10 3.43 20 126.47 0.07 229.77 0.44 228.15 0.11 336.20 0.42 624.09 0.36 1 028.00 1.95 30 126.78 0.03 231.86 0.21 228.63 0.05 337.92 0.17 622.84 0.13 1 036.20 0.82 40 126.87 0.01 232.58 0.07 228.77 0.01 340.89 0.30 622.85 0 1 038.00 0.18 50 126.89 0 232.90 0.03 228.82 0 341.19 0.03 622.77 0.01 1 038.70 0.07 60 126.88 0 233.07 0.02 228.84 0 340.89 0.03 622.67 0.01 1 039.00 0.03 70 126.87 0 233.16 0.01 228.84 0 340.82 0.01 622.58 0.01 1 039.20 0.02 80 126.86 0 233.22 0.01 228.84 0 340.79 0 622.48 0.01 1 039.20 0 90 126.84 0 233.26 0 228.84 0 340.77 0 622.38 0.01 1 039.20 0 ![]()
图 2 V形连接板固有频率随耦合角度α的变化规律Figure 2. The variation of the natural frequency of the V-shaped connector plate with the coupling angle α由图2可见，V形连接板(m, n)阶固有频率随α增加呈现出2个阶段的变化规律，第1个阶段是当α较小时固有频率急剧提升，第2个阶段是当α增大到一定值以后，固有频率变化较小。若以V形连接板各阶固有频率的变化率κ1≤0.3为判定其固有频率基本保持稳定的依据，则通过表4可以看出角度α在0°～40°范围内时固有频率急剧提升，角度α在40°～90°范围内时固有频率变化较小。这是由于V形连接板是由2块板耦合而成，当α=0°时，2块平板在耦合位置处的法向支撑度最小，随着α从0°逐渐增加，2块平板耦合位置处法向上的支撑度逐渐提升，相当于逐渐加固2块板的耦合位置，提升了V形连接板的固有频率。当α达到一定值后，2块板耦合位置处法向上的支撑度趋于稳定，因此固有频率不随α的改变而大幅变化。
3. 附板厚度对V形连接板本征动力特性的影响
3.1 V形连接板附板厚度选取范围
分析附板厚度对V形连接板固有频率与振型的影响。在船舶与海洋工程结构中，不同位置所使用的钢板厚度不同，考虑到实际工程中船舶与海洋工程结构钢板厚度的使用情况，本文在数值计算过程中附板厚度h1分别选取3，4，5，…，24，25 mm，其余材料属性与几何参数见表1，计算V形连接板的固有频率与振型。
3.2 附板厚度对V形连接板本征动力特性的影响分析
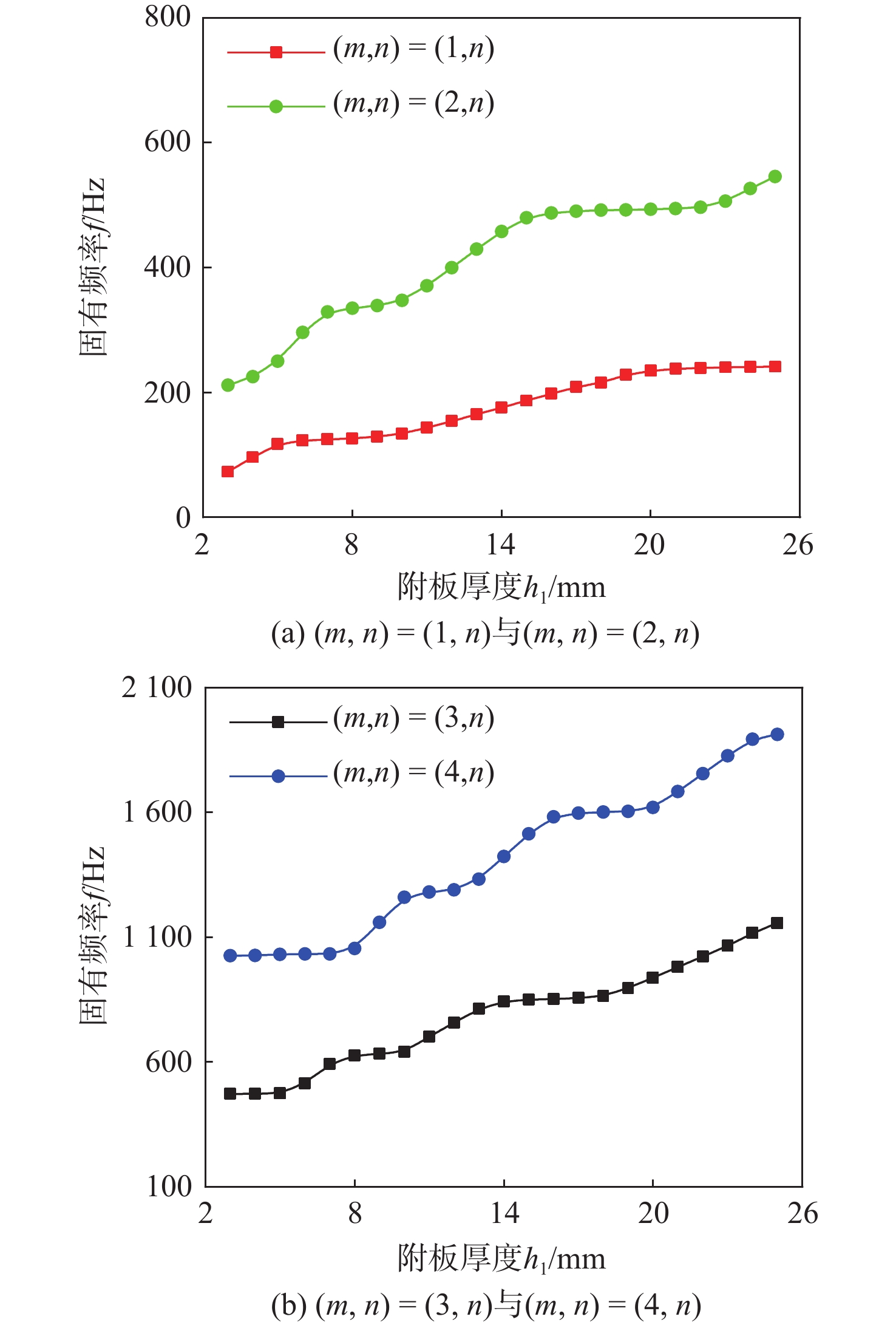
在分析附板厚度对V形连接板本征动力特性的影响时，同样选取主板上(m, n)阶模态为研究对象。主板上(m, n)阶固有频率及其随附板厚度的变化率κ2见表5，固有频率随附板厚度的变化规律如图3所示。(m, n)=(3, n)时主板上振型随附板厚度变化的振型如图4所示。表5中变化率κ2为相邻附板厚度固有频率变化量绝对值与附板厚度变化量绝对值的比值。
表 5 不同附板厚度下V形连接板主板第(m, n)阶模态固有频率f及其变化率κ2Table 5. The (m, n)-order natural frequencies f and their variation rate κ2 of V-shaped plates under different thickness of the attached plate附板厚度h1/mm (1, n) (2, n) (3, n) (4, n) f/Hz κ2 f/Hz κ2 f/Hz κ2 f/Hz κ2 3 72.53 — 211.34 — 472.06 — 1 025.90 — 4 96.07 23.54 225.06 13.72 473.39 1.33 1 026.90 1.00 5 117.06 20.99 249.87 24.81 473.84 0.45 1 031.00 4.10 6 122.52 5.46 295.97 46.10 514.40 40.56 1 033.10 2.10 7 124.39 1.87 328.89 32.92 592.86 78.46 1 033.20 0 8 126.30 1.91 334.77 5.88 626.96 34.10 1 055.00 21.90 9 128.84 2.54 338.86 4.09 633.21 6.25 1 159.70 104.70 10 134.02 5.18 347.35 8.49 640.51 7.30 1 260.30 100.60 11 143.25 9.23 370.72 23.37 701.86 61.35 1 280.90 20.60 12 153.86 10.61 399.81 29.09 758.24 56.38 1 289.70 8.80 13 164.78 10.92 429.36 29.55 812.71 54.47 1 333.10 43.40 14 175.77 10.99 457.78 28.42 842.75 30.04 1 423.90 90.80 15 186.76 10.99 479.71 21.93 850.94 8.19 1 514.70 90.80 16 197.67 10.91 487.62 7.91 852.42 1.48 1 582.70 68.00 17 208.41 10.74 490.35 2.73 856.33 3.91 1 598.00 15.30 18 218.75 10.34 492.12 1.77 864.79 8.46 1 601.60 3.60 19 227.97 9.22 492.30 0.18 896.43 31.64 1 604.90 3.30 20 234.44 6.47 493.55 1.25 938.28 41.85 1 620.20 15.30 21 237.64 3.20 494.64 1.09 981.06 42.78 1 684.20 64.00 22 239.20 1.56 496.71 2.07 1 023.40 42.34 1 755.70 71.50 23 240.13 0.93 506.25 9.54 1 065.70 42.30 1 827.10 71.40 24 240.76 0.63 526.59 20.34 1 117.10 51.40 1 894.20 67.10 25 241.23 0.47 545.88 19.29 1 157.60 40.50 1 913.00 18.80 ![]()
图 3 V形连接板固有频率随附板厚度的变化规律Figure 3. The variation law of natural frequency of V-shaped connecting plate with the thickness of the attached plate![]()
图 4 不同附板厚度下(m, n)=(3, n)时V形连接板典型振型Figure 4. Typical mode shapes of V-shaped connecting plate at (m, n)=(3, n) under different thicknesses of the attached plate针对平板模型固有频率与模态的研究比较充分和成熟。根据经典薄板理论，四边简支矩形薄板固有频率与尺寸和模态数之间的关系可以表示为[18]：
fmn=12π √D′ρ′h′[(mπ L′y)2+(nπ L′x)2] (1) 式中：D'=Eh'3/[12(1－ν2)]，为薄板的弯曲刚度；h'为薄板厚度。由式(1)可知，四边简支矩形薄板的固有频率fmn与h’成正比。
由于V形连接板仅附板厚度h1发生了变化而主板厚度保持不变，且V形连接板边界条件为各边自由，因此，无论是主板还是附板，其固有频率与板厚不再严格成正比，但从图3可以看出V形连接板的固有频率依然随着h1的增加而提高。
由图3可以看出，V形连接板各阶固有频率随着附板厚度h1的增加呈阶梯式提高，附板厚度在某些区间内固有频率的变化率较大，呈非线性变化规律，而在另一些区间内固有频率的变化率较小，大体上呈线性变化规律。如图4所示，附板厚度变化下V形连接板(m, n)=(3, n)阶振型图表明随着h1增加，主板Ly方向上的模态数m保持不变，而Lx方向模态数n逐渐从2增加到4。对比图3与图4可见，V形连接板固有频率变化率较大的区间与V形连接板模态转化区间一致，即模态转化的同时，固有频率发生较大变化。(m, n)=(1, n)，(m, n)=(2, n)，(m, n)=(4, n)时具有相似的变化规律，上述现象也可用式(1)来解释。
由式(1)可知，在平板材料属性、几何尺寸以及Lx和Ly方向上的模态数保持不变的情况下，四边简支矩形薄板的固有频率与板厚h成正比。而当平板材料属性、几何尺寸以及Ly方向上的模态数m保持不变，Lx方向上的模态数n增加时，四边简支矩形薄板的固有频率随厚度的增加而线性增大，随Lx方向上的模态数n的增加而非线性增大，由于附板厚度的数量级远比模态数n的数量级小，因此，当V形连接板主板上模态数n增加时，固有频率相较于模态未发生转变时变化更加显著。因此，V形连接板固有频率随附板厚度h1增加呈线性增大与非线性增大交替出现的阶梯式增大现象。考虑到V形连接板耦合特征以及边界条件的影响，虽然固有频率不再与n2严格成正比，但模态数n增加时，依然会导致固有频率显著提高。由图3与表5还可以看出V形连接板模态发生转变的过程中，固有频率与附板厚度的关系近似正比例关系。例如从(m, n)=(1, 1)转变为(m, n)=(1, 2)的过程中，变化率保持在10.99左右。
4. 附板长度对V形连接板本征动力特性的影响
4.1 V形连接板附板长度选取范围
分析附板长度对V形连接板固有频率与振型的影响，除了附板长度外，其余材料参数与几何参数见表1。V形连接板由附板与主板两部分组成，在板厚相差不大的情况下，附板长度对V形连接板的动力特性具有重要影响。为了研究主板与附板耦合程度较高情况下附板长度对V形连接板固有频率与振型的影响，以附板长度为主板长度的35%和150%为界限，附板长度L分别取0.35，0.40，0.45，…，1.40，1.50 m，以此计算V形连接板的固有频率与振型。
4.2 附板长度对V形连接板本征动力特性的影响分析
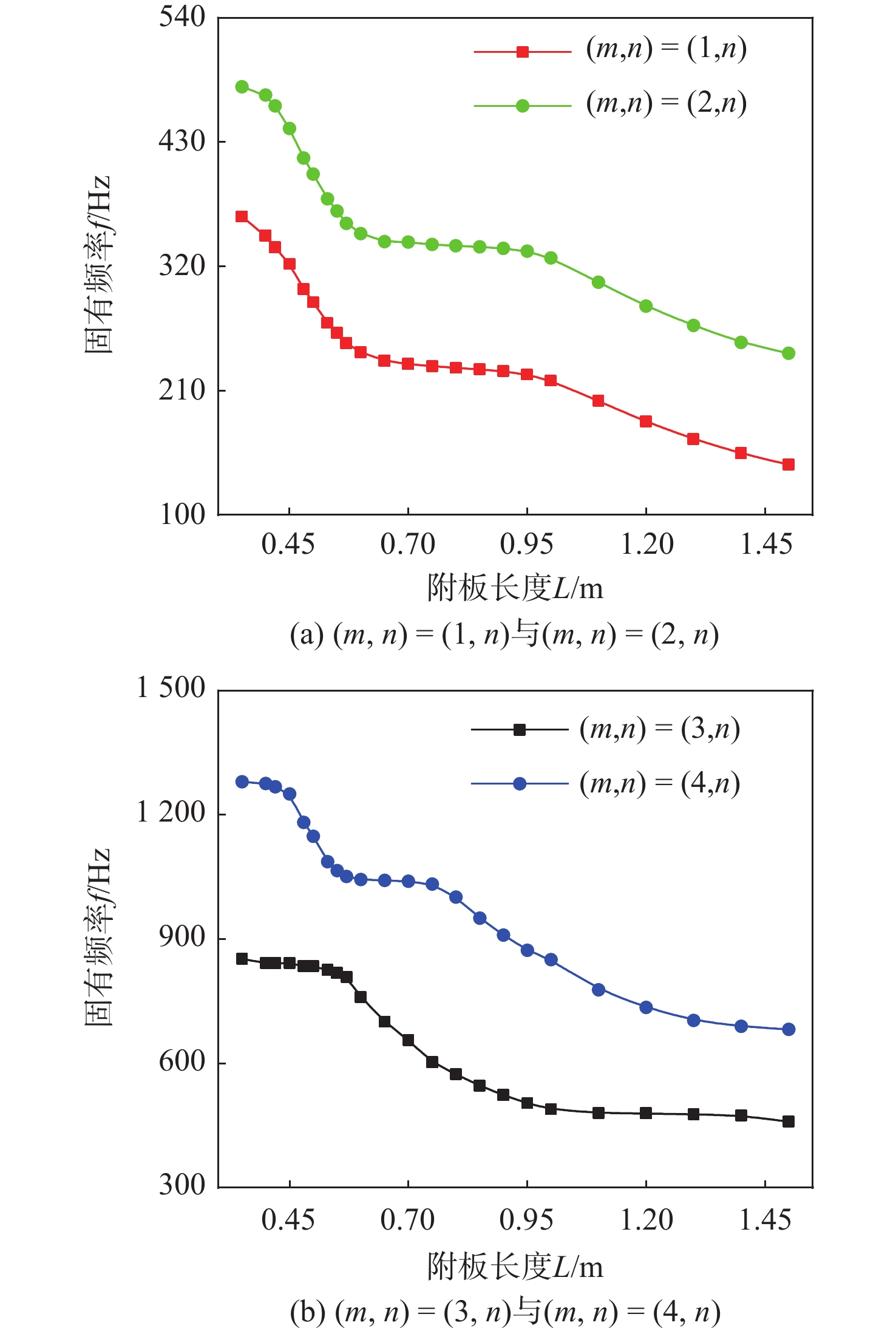
与分析附板厚度对V形连接板本征动力特性的影响时相似，在分析附板长度对V形连接板本征动力特性的影响时也选取主板第(m, n)阶模态为研究对象。主板上(m, n)阶固有频率及其随附板长度的变化率κ3见表6。固有频率随附板长度的变化规律如图5所示。主板第(m, n)=(4, n)阶振型随附板长度的变化规律如图6所示。变化率κ3为相邻附板长度固有频率变化量绝对值与附板长度变化量绝对值的比值。
表 6 不同附板长度下V形连接板主板第(m, n)阶f模态固有频率及其变化率κ3Table 6. The (m, n)-order natural frequencies f and their variation rate κ3 of V-shaped plates under different length of the attached plate附板长度L/cm (1, n) (2, n) (3, n) (4, n) f/Hz κ3 f/Hz κ3 f/Hz κ3 f/Hz κ3 35 355.06 — 478.88 — 852.35 — 1 279.90 — 40 346.92 3.39 471.52 1.47 842.12 2.05 1 275.40 0.90 45 321.99 4.88 442.05 6.63 842.20 0.03 1 250.40 5.70 48 299.95 7.35 415.87 8.73 834.58 2.54 1 182.00 22.80 50 288.24 5.85 401.63 7.12 834.72 0.07 1 148.40 16.80 53 270.02 6.07 379.64 7.33 825.28 3.15 1 086.99 20.47 55 261.00 4.51 369.01 5.31 818.10 3.59 1 065.40 10.79 57 251.95 4.53 357.97 5.52 788.94 4.96 1 051.20 7.10 60 243.83 2.71 348.87 3.03 759.79 16.13 1 044.00 2.40 65 236.46 1.47 341.87 1.40 700.41 11.88 1 041.60 0.48 70 233.37 0.62 341.47 0.08 655.79 8.92 1 039.70 0.38 75 231.58 0.36 339.30 0.43 602.42 10.67 1 032.70 1.40 80 230.21 0.27 338.23 0.21 573.75 5.73 1 001.40 6.26 85 228.82 0.28 337.22 0.20 546.49 5.45 950.57 10.17 90 227.04 0.36 335.86 0.27 523.45 4.61 909.66 8.18 95 224.16 0.58 333.34 0.50 503.86 3.92 873.08 7.32 100 218.81 1.07 327.42 1.18 489.20 2.93 850.25 4.57 110 200.82 1.80 305.80 2.16 480.52 0.87 777.60 7.26 120 182.54 1.83 284.76 2.10 479.50 0.10 735.27 4.23 130 167.10 1.54 267.53 1.72 477.33 0.22 703.74 3.15 140 154.45 1.27 252.66 1.49 474.56 0.28 689.48 1.43 150 144.32 1.01 243.05 0.96 459.50 1.51 682.11 0.74 ![]()
图 5 V形连接板固有频率随附板长度的变化规律Figure 5. The natural frequency of the V-shaped plate varies with the length of the attached plate![]()
图 6 不同附板长度下 (m, n)=(3, n)时V形连接板典型振型Figure 6. Typical mode shapes of V-shaped connecting plate at (m, n)=(3, n) under different length of the attached plate由式(1)可知，平板模型第(m, n)阶固有频率fmn与Lx2成反比，与n2成正比。对于平板模型，固有频率随着长度Lx的增大而降低，随着模态数n减小而降低。由于V形连接板仅附板长度发生了变化而主板长度保持不变，且V形连接板边界条件为各边自由，因此，无论是主板还是附板，固有频率fmn虽然不再严格与Lx2成反比，但从图5中依然可以看出(m, n)阶固有频率仍然会随着长度的增加而降低。
通过图6发现，随着附板长度L增加，主板Ly方向模态数m保持不变，而Lx方向模态数n随着附板长度的增加而逐渐减小，(m, n)=(3, 4)阶振型逐渐转化为(m, n)=(3, 2)阶振型。结合图5和图6发现，在(m, n)=(3, n)时，在部分模态转化现象发生的附板长度区间内固有频率快速降低，而在另一部分模态转化的附板区间内固有频率变化不明显。其他模态(m, n)=(1, n)，(m, n)=(2, n)，(m, n)=(4, n)具有相似的变化规律。根据式(1)，固有频率在部分区间内快速降低的原因是模态数n减小。
5. V形连接板与孤立板动力相似研究
前面研究了V形连接板耦合角度、附板厚度与附板长度等几何参数对其动力特性的影响，计算结果表明V形连接板固有频率随附板厚度增加而阶梯式提高，这与一边弹性支撑，另外三边自由边界条件下正交加筋板动力特性随着弹性边支撑刚度的变化规律有一定的相似之处[19]。为了探讨这两种相似变化规律之间的联系，开展V形连接板与孤立板动力相似性研究。
5.1 弹性支撑孤立板动力特性研究
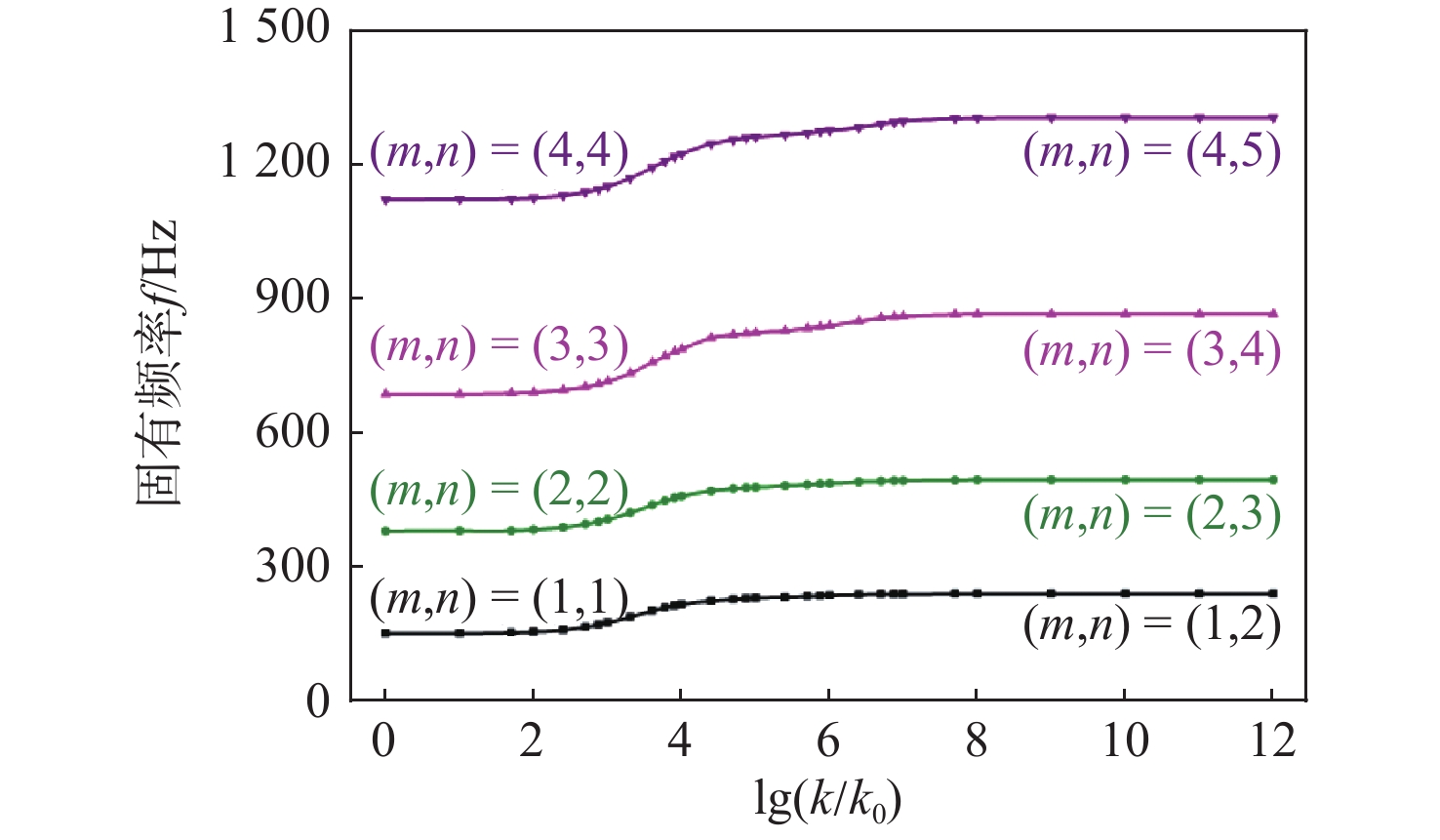
如图7所示，以一边弹性支撑，另外三边自由的单位尺度孤立板模型为研究对象，计算其在不同弹性支撑刚度下的固有频率与振型，其材料属性和几何参数与V形连接板中主板参数相同。其中孤立板的弹性支撑边用弹簧模拟，使孤立板一条边的每一个节点都与相同刚度的弹簧相连接，弹簧的另一端连接在地面，弹簧与节点的6个自由度耦合。表7列出了不同弹性支撑刚度下单位尺度孤立板固有频率及其变化率κ4，图8为单位尺度孤立板固有频率随支撑刚度的变化规律图，图中k为弹性支撑刚度，k0为单位刚度，其大小为1 N/m。图9为孤立板第(m, n)=(1, n)阶模态随弹性支撑刚度变化的振型图。
表 7 不同弹性支撑刚度下单位尺度孤立板固有频率f及其变化率κ4Table 7. The natural frequency f and their variation rate κ4 of isolated plate under different elastic support stiffnesslg(k/k0) (1, n) (2, n) (3, n) (4, n) f/Hz κ4 f/Hz κ4 f/Hz κ4 f/Hz κ4 0 155.61 — 383.27 — 688.23 — 1 121.40 — 1.000 0 155.96 0.35 383.63 0.36 688.57 0.34 1 121.70 0.30 2.000 0 159.14 3.18 386.99 3.36 691.89 3.32 1 125.10 3.40 2.397 9 163.72 11.51 391.96 12.49 696.99 12.82 1 130.30 13.07 2.699 0 169.85 20.36 398.93 23.15 704.48 24.88 1 137.90 25.24 3.000 0 179.82 33.12 409.74 35.91 716.78 40.86 1 150.40 41.53 3.310 3 192.33 40.32 424.62 47.95 734.32 56.53 1 168.70 58.98 3.602 1 205.91 46.54 441.86 59.08 758.97 84.48 1 191.90 79.51 3.778 2 212.98 40.15 451.43 54.34 772.96 79.44 1 206.30 81.77 4.000 0 220.12 32.19 461.47 45.27 788.71 71.01 1 223.20 76.19 4.397 9 228.12 20.11 472.92 28.78 813.25 61.67 1 244.90 54.54 4.699 0 231.59 11.52 477.57 15.44 820.02 22.48 1 254.30 31.22 5.000 0 234.90 11.00 480.53 9.83 825.05 16.71 1 260.00 18.94 5.397 9 236.51 4.05 483.73 8.04 829.22 10.48 1 265.20 13.07 6.000 0 240.75 7.04 489.33 9.30 841.05 19.65 1 274.90 16.11 7.000 0 243.70 2.95 495.82 6.49 861.34 20.29 1 295.30 20.40 8.000 0 244.12 0.42 497.01 1.19 865.96 4.62 1 302.30 7.00 9.000 0 244.17 0.05 497.14 0.13 866.51 0.55 1 303.10 0.80 10.000 0 244.18 0.01 497.15 0.01 866.58 0.07 1 303.20 0.10 11.000 0 244.18 0 497.16 0.01 866.59 0.01 1 303.20 0 12.000 0 244.18 0 497.16 0 866.59 0 1 303.20 0 ![]()
图 8 单位尺度孤立板固有频率随弹性支撑刚度变化规律Figure 8. The variation of the natural frequency of the unit scale isolated plate with the elastic support stiffness![]()
图 9 不同弹性支撑刚度下 (m, n)=(1, n)时单位尺度孤立板典型振型Figure 9. Typical mode shapes of isolated plate at (m, n)=(1, n) under different elastic support stiffness由图8可知，单位尺度孤立板的各阶固有频率随着弹性支撑刚度的提高，从较低频率提高到较高频率。结合表7中(m, n)=(1, n)时单位尺度孤立板固有频率与弹性支撑刚度的对应关系可以发现，在lg(k/k0) < 2时，孤立板固有频率随弹性支撑刚度的变化较小，变化率κ4小于4，此时弹性支撑刚度非常小，加筋板的弹性支撑边近似为自由边界条件。当2 ≤lg(k/k0)≤ 6时，孤立板固有频率随弹性支撑刚度增大而显著提高，变化率κ4大于4，此时孤立板一边为弹性支撑边界条件，该刚度区间为本文所述孤立板模型的刚度敏感区间[19]。当lg(k/k0) > 6时，孤立板固有频率随弹性支撑刚度的变化也较小，变化率κ4小于4，此时弹性支撑刚度非常大，孤立板的弹性支撑边近似为固支边界条件。(m, n)=(2, n)，(m, n)=(3, n)，(m, n)=(4, n)等模态具有相似的变化规律。
从图9可以看出随着弹性支撑刚度的增大，孤立板的模态逐渐从(m, n)=(1, 1)转变为(m, n)=(1, 2)，并且结合图8发现敏感刚度区间正是模态发生转化的区间。
5.2 V形连接板与孤立板动力相似
前述分析得出的孤立板的固有频率和振型随弹性支撑刚度的变化规律，与V形连接板附板厚度参数研究得出的规律有相似之处，都是从一个频率提升到另一个频率，并且频率变化的同时模态发生转变。由V形连接板耦合角度的参数化分析发现：α在40°～90°范围时，V形连接板固有频率不随角度α的变化而显著变化（变化率不大于0.3），因此，当耦合角度α在40°～90°范围时，若将附板看作主板的边界条件，则附板在这部分角度区间内为主板提供的边界条件是稳定的。
在附板厚度的参数化分析中，设置α=60°，处于40°～90°范围。如图9所示，将从V形连接板附板厚度的参数化分析中得到的振型与孤立板动力特性研究中弹性支撑刚度k=1 013 N/m(可以看作固支)时的振型进行对比。每个振型对应的固有频率见表8。V形连接板振型图的选取原则为振型在V形连接板附板厚度改变时保持稳定，即从图3中曲线较平缓的区间中选取。弹性支撑板振型图的选取则为寻找与V形连接板主板上振型图相似的振型。
表 8 V形连接板固有频率与弹性支撑孤立板固有频率对比Table 8. Comparison of natural frequency between V-shaped plate and elastic support isolated plate(m, n)阶
模态V形连接板
固有频率f/Hz弹性支撑矩形板
固有频率f/Hz相对
变化/%(1, 1) 128.84 133.45 3.45 (1, 2) 240.13 244.18 1.66 (2, 2) 338.86 349.21 2.96 (2, 3) 492.30 497.15 0.98 (3, 3) 633.21 649.39 2.49 (3, 4) 852.42 866.58 1.63 (4, 4) 1 033.10 1 066.80 3.26 (4, 5) 1 289.70 1 303.20 1.04 图10为V形连接板振型与弹性支撑孤立板振型对比图，其中(a)～(d)和(i)～(l)小图为附板厚度参数化分析中V形连接板各阶振型图，(e)～(h)和(m)～(p)小图为弹性支撑孤立板在弹性支撑刚度k=1 013 N/m时的各阶振型图。如图10所示，V形连接板的振型皆能从孤立板弹性支撑刚度为k=1013 N/m时找到对应的振型。由表8可知，V形连接板与孤立板在振型相似时，它们的固有频率接近（相对变化小于4%），但V形连接板的固有频率比弹性支撑孤立板的固有频率低，这是由于采用弹性支撑孤立板等效V形连接板附板对主板的动力特性影响时，只考虑了刚度，而忽略了质量。这说明当α=60°时，附板相当于给主板提供了一个近似固支的边界条件。再结合V形连接板耦合角度的参数化分析进一步说明α在40°～90°范围时，附板相当于给主板提供了一个固支边界条件（主板与附板弯曲刚度相当[20]）。
![]()
图 10 V形连接板振型与弹性支撑孤立板振型对比图形Figure 10. Comparison diagram of V-shaped plate modes and isolated plate modes在V形连接板主板模态发生转变时，其固有频率与附板厚度近似为正比例关系。当V形板耦合角度在40°到90°范围内时，附板相当于为主板提供了一个固支边界条件。因此，若α在40°～90°范围内且V形连接板第(m, n)阶振型对应附板厚度为ha，第(m, n+1)阶振型对应附板厚度为hb，则V形连接板的第(m, n)阶固有频率与第(m, n+1)阶固有频率可以通过将弹性支撑孤立板的一条边设置为固支，其余边设为自由求出。通过将第(m, n+1)阶固有频率减去(m, n)阶固有频率得到差值，然后用该差值除以hb－ha就可以得出模态转化过程中频率的增速。若ha和hb恰好是模态转化的起始和结束时的附板厚度，则利用这个规律还可以求出附板厚度区间(ha, hb)中任意附板厚度所对应的固有频率。由此得到V形连接板在附板厚度变化时特定模态固有频率的快速预报方法。
6. 结 论
本文以V形连接板和孤立板为研究对象，采用有限元法计算了不同耦合角度、不同附板厚度以及不同附板长度下的固有频率与振型，分析了耦合角度、附板厚度与长度等参数对V形连接板动力特性与模态转换现象的影响规律，阐明了V形连接板动力特性的角度敏感性问题与模态转换机理。通过对比V形连接板模型与孤立板模型动力特性，得到了V形连接板边界动力等效关系，在此基础上形成了V形连接板部分模态对应固有频率的快速预报方法。主要结论如下：
1) 耦合角度α在40°～90°范围内时，V形连接板的固有频率不随角度α的变化而明显变化，附板为主板提供了近似固支的边界条件。
2) V形连接板附板厚度增大在保持Ly方向模态数m不变的同时会增大Lx方向模态数n，固有频率随附板厚度增加单调递增；附板长度增大在保持Ly方向模态数m不变的同时会减小Lx方向模态数n，固有频率随附板长度增加单调递减。
3) V形连接板固有频率随附板厚度增加呈阶梯状变化，主板模态转化时，固有频率随附板厚度增大而非线性提高，模态稳定时，固有频率随附板厚度增大而线性提高。
4) 在工程中，对于α在40°～90°范围内的V形连接板，可以通过计算一边固支，另外三边自由边界条件下矩形板的固有频率来快速预报特定模态的固有频率。
-
![]()
图 2 V形连接板固有频率随耦合角度α的变化规律
Figure 2. The variation of the natural frequency of the V-shaped connector plate with the coupling angle α
![]()
图 3 V形连接板固有频率随附板厚度的变化规律
Figure 3. The variation law of natural frequency of V-shaped connecting plate with the thickness of the attached plate
![]()
图 4 不同附板厚度下(m, n)=(3, n)时V形连接板典型振型
Figure 4. Typical mode shapes of V-shaped connecting plate at (m, n)=(3, n) under different thicknesses of the attached plate
![]()
图 5 V形连接板固有频率随附板长度的变化规律
Figure 5. The natural frequency of the V-shaped plate varies with the length of the attached plate
![]()
图 6 不同附板长度下 (m, n)=(3, n)时V形连接板典型振型
Figure 6. Typical mode shapes of V-shaped connecting plate at (m, n)=(3, n) under different length of the attached plate
![]()
图 8 单位尺度孤立板固有频率随弹性支撑刚度变化规律
Figure 8. The variation of the natural frequency of the unit scale isolated plate with the elastic support stiffness
![]()
图 9 不同弹性支撑刚度下 (m, n)=(1, n)时单位尺度孤立板典型振型
Figure 9. Typical mode shapes of isolated plate at (m, n)=(1, n) under different elastic support stiffness
![]()
图 10 V形连接板振型与弹性支撑孤立板振型对比图形
Figure 10. Comparison diagram of V-shaped plate modes and isolated plate modes
表 1 V形连接板数值模型材料属性和几何参数
Table 1 Material properties and geometric parameters of V-shaped plate
参数 数值 弹性模量E/Pa 2.1×1011 密度ρ/(kg·m−3) 7 800 泊松比v 0.3 主板厚度h/m 0.01 主板长度Lx/m 1.00 主板宽度Ly/m 1.00 附板厚度h1/m 0.01 附板长度L/m 0.70 加强筋高度H/m 0.02 加强筋宽度B/m 0.01 V形板夹角的补角α/（°） 60 
下载: 导出CSV
表 2 不同网格尺寸下V形连接板的固有频率及其最大差值
Table 2 Natural frequencies and their maximum differences of V-shaped connecting plates under different grid sizes
网格属性 不同阶数(m, n)的固有频率 最大差值/% 尺寸/m 网格数量 (1, 1) (2, 2) (3, 3) (4, 4) 0.010 17 924 127.07 341.98 625.64 1 042.46 — 0.009 22 516 127.04 341.89 625.36 1 041.82 0.061 0.008 28 360 127.02 341.81 625.14 1 041.31 0.049 0.007 36 427 127.00 341.73 624.94 1 040.83 0.046 0.006 49 933 126.98 341.66 624.74 1 040.42 0.041 0.005 71 422 126.95 341.59 624.57 1 040.03 0.036 0.004 110 299 126.94 341.54 624.43 1 039.71 0.032 0.003 197 003 126.93 341.50 624.32 1 039.51 0.019 0.002 433 856 126.92 341.47 624.27 1 039.34 0.019
下载: 导出CSV
表 3 本文结果与文献[5]结果对比
Table 3 Comparison between the results of this article and those of Reference [5]
模态阶数 文献[5]固有频率/Hz 本文固有频率/Hz 误差/% 1 24.24 24.29 0.21 2 30.88 30.84 0.13 3 61.25 61.07 0.29 4 69.25 69.26 0.01 5 117.46 117.27 0.16
下载: 导出CSV
表 4 不同耦合角度α下V形连接板主板第(m, n)阶模态固有频率f及其变化率κ1
Table 4 The (m, n)-order natural frequencies f and their variation rate κ1 of V-shaped plates under different coupling angles α
α/(°) (1, 1) (1, 2) (2, 1) (2, 2) (3, 3) (4, 4) f/Hz κ1 f/Hz κ1 f/Hz κ1 f/Hz κ1 f/Hz κ1 f/Hz κ1 0 97.09 — 198.63 — 196.69 — 307.53 — 531.24 — 934.07 — 3 109.20 4.04 200.55 0.64 205.07 2.79 309.49 0.65 536.77 1.84 944.82 3.58 6 119.96 3.59 207.28 2.24 218.48 4.47 315.73 2.08 554.57 5.93 954.14 3.11 9 123.94 1.33 216.73 3.15 224.28 1.93 323.97 2.75 580.85 8.76 973.66 6.51 12 125.36 0.47 223.26 2.18 226.45 0.72 329.93 1.99 608.80 9.32 996.29 7.54 15 125.99 0.21 226.85 1.20 227.43 0.33 333.37 1.15 621.25 4.15 1 013.80 5.84 18 126.33 0.11 228.89 0.68 227.94 0.17 335.35 0.66 623.38 0.71 1 024.10 3.43 20 126.47 0.07 229.77 0.44 228.15 0.11 336.20 0.42 624.09 0.36 1 028.00 1.95 30 126.78 0.03 231.86 0.21 228.63 0.05 337.92 0.17 622.84 0.13 1 036.20 0.82 40 126.87 0.01 232.58 0.07 228.77 0.01 340.89 0.30 622.85 0 1 038.00 0.18 50 126.89 0 232.90 0.03 228.82 0 341.19 0.03 622.77 0.01 1 038.70 0.07 60 126.88 0 233.07 0.02 228.84 0 340.89 0.03 622.67 0.01 1 039.00 0.03 70 126.87 0 233.16 0.01 228.84 0 340.82 0.01 622.58 0.01 1 039.20 0.02 80 126.86 0 233.22 0.01 228.84 0 340.79 0 622.48 0.01 1 039.20 0 90 126.84 0 233.26 0 228.84 0 340.77 0 622.38 0.01 1 039.20 0
下载: 导出CSV
表 5 不同附板厚度下V形连接板主板第(m, n)阶模态固有频率f及其变化率κ2
Table 5 The (m, n)-order natural frequencies f and their variation rate κ2 of V-shaped plates under different thickness of the attached plate
附板厚度h1/mm (1, n) (2, n) (3, n) (4, n) f/Hz κ2 f/Hz κ2 f/Hz κ2 f/Hz κ2 3 72.53 — 211.34 — 472.06 — 1 025.90 — 4 96.07 23.54 225.06 13.72 473.39 1.33 1 026.90 1.00 5 117.06 20.99 249.87 24.81 473.84 0.45 1 031.00 4.10 6 122.52 5.46 295.97 46.10 514.40 40.56 1 033.10 2.10 7 124.39 1.87 328.89 32.92 592.86 78.46 1 033.20 0 8 126.30 1.91 334.77 5.88 626.96 34.10 1 055.00 21.90 9 128.84 2.54 338.86 4.09 633.21 6.25 1 159.70 104.70 10 134.02 5.18 347.35 8.49 640.51 7.30 1 260.30 100.60 11 143.25 9.23 370.72 23.37 701.86 61.35 1 280.90 20.60 12 153.86 10.61 399.81 29.09 758.24 56.38 1 289.70 8.80 13 164.78 10.92 429.36 29.55 812.71 54.47 1 333.10 43.40 14 175.77 10.99 457.78 28.42 842.75 30.04 1 423.90 90.80 15 186.76 10.99 479.71 21.93 850.94 8.19 1 514.70 90.80 16 197.67 10.91 487.62 7.91 852.42 1.48 1 582.70 68.00 17 208.41 10.74 490.35 2.73 856.33 3.91 1 598.00 15.30 18 218.75 10.34 492.12 1.77 864.79 8.46 1 601.60 3.60 19 227.97 9.22 492.30 0.18 896.43 31.64 1 604.90 3.30 20 234.44 6.47 493.55 1.25 938.28 41.85 1 620.20 15.30 21 237.64 3.20 494.64 1.09 981.06 42.78 1 684.20 64.00 22 239.20 1.56 496.71 2.07 1 023.40 42.34 1 755.70 71.50 23 240.13 0.93 506.25 9.54 1 065.70 42.30 1 827.10 71.40 24 240.76 0.63 526.59 20.34 1 117.10 51.40 1 894.20 67.10 25 241.23 0.47 545.88 19.29 1 157.60 40.50 1 913.00 18.80
下载: 导出CSV
表 6 不同附板长度下V形连接板主板第(m, n)阶f模态固有频率及其变化率κ3
Table 6 The (m, n)-order natural frequencies f and their variation rate κ3 of V-shaped plates under different length of the attached plate
附板长度L/cm (1, n) (2, n) (3, n) (4, n) f/Hz κ3 f/Hz κ3 f/Hz κ3 f/Hz κ3 35 355.06 — 478.88 — 852.35 — 1 279.90 — 40 346.92 3.39 471.52 1.47 842.12 2.05 1 275.40 0.90 45 321.99 4.88 442.05 6.63 842.20 0.03 1 250.40 5.70 48 299.95 7.35 415.87 8.73 834.58 2.54 1 182.00 22.80 50 288.24 5.85 401.63 7.12 834.72 0.07 1 148.40 16.80 53 270.02 6.07 379.64 7.33 825.28 3.15 1 086.99 20.47 55 261.00 4.51 369.01 5.31 818.10 3.59 1 065.40 10.79 57 251.95 4.53 357.97 5.52 788.94 4.96 1 051.20 7.10 60 243.83 2.71 348.87 3.03 759.79 16.13 1 044.00 2.40 65 236.46 1.47 341.87 1.40 700.41 11.88 1 041.60 0.48 70 233.37 0.62 341.47 0.08 655.79 8.92 1 039.70 0.38 75 231.58 0.36 339.30 0.43 602.42 10.67 1 032.70 1.40 80 230.21 0.27 338.23 0.21 573.75 5.73 1 001.40 6.26 85 228.82 0.28 337.22 0.20 546.49 5.45 950.57 10.17 90 227.04 0.36 335.86 0.27 523.45 4.61 909.66 8.18 95 224.16 0.58 333.34 0.50 503.86 3.92 873.08 7.32 100 218.81 1.07 327.42 1.18 489.20 2.93 850.25 4.57 110 200.82 1.80 305.80 2.16 480.52 0.87 777.60 7.26 120 182.54 1.83 284.76 2.10 479.50 0.10 735.27 4.23 130 167.10 1.54 267.53 1.72 477.33 0.22 703.74 3.15 140 154.45 1.27 252.66 1.49 474.56 0.28 689.48 1.43 150 144.32 1.01 243.05 0.96 459.50 1.51 682.11 0.74
下载: 导出CSV
表 7 不同弹性支撑刚度下单位尺度孤立板固有频率f及其变化率κ4
Table 7 The natural frequency f and their variation rate κ4 of isolated plate under different elastic support stiffness
lg(k/k0) (1, n) (2, n) (3, n) (4, n) f/Hz κ4 f/Hz κ4 f/Hz κ4 f/Hz κ4 0 155.61 — 383.27 — 688.23 — 1 121.40 — 1.000 0 155.96 0.35 383.63 0.36 688.57 0.34 1 121.70 0.30 2.000 0 159.14 3.18 386.99 3.36 691.89 3.32 1 125.10 3.40 2.397 9 163.72 11.51 391.96 12.49 696.99 12.82 1 130.30 13.07 2.699 0 169.85 20.36 398.93 23.15 704.48 24.88 1 137.90 25.24 3.000 0 179.82 33.12 409.74 35.91 716.78 40.86 1 150.40 41.53 3.310 3 192.33 40.32 424.62 47.95 734.32 56.53 1 168.70 58.98 3.602 1 205.91 46.54 441.86 59.08 758.97 84.48 1 191.90 79.51 3.778 2 212.98 40.15 451.43 54.34 772.96 79.44 1 206.30 81.77 4.000 0 220.12 32.19 461.47 45.27 788.71 71.01 1 223.20 76.19 4.397 9 228.12 20.11 472.92 28.78 813.25 61.67 1 244.90 54.54 4.699 0 231.59 11.52 477.57 15.44 820.02 22.48 1 254.30 31.22 5.000 0 234.90 11.00 480.53 9.83 825.05 16.71 1 260.00 18.94 5.397 9 236.51 4.05 483.73 8.04 829.22 10.48 1 265.20 13.07 6.000 0 240.75 7.04 489.33 9.30 841.05 19.65 1 274.90 16.11 7.000 0 243.70 2.95 495.82 6.49 861.34 20.29 1 295.30 20.40 8.000 0 244.12 0.42 497.01 1.19 865.96 4.62 1 302.30 7.00 9.000 0 244.17 0.05 497.14 0.13 866.51 0.55 1 303.10 0.80 10.000 0 244.18 0.01 497.15 0.01 866.58 0.07 1 303.20 0.10 11.000 0 244.18 0 497.16 0.01 866.59 0.01 1 303.20 0 12.000 0 244.18 0 497.16 0 866.59 0 1 303.20 0
下载: 导出CSV
表 8 V形连接板固有频率与弹性支撑孤立板固有频率对比
Table 8 Comparison of natural frequency between V-shaped plate and elastic support isolated plate
(m, n)阶
模态V形连接板
固有频率f/Hz弹性支撑矩形板
固有频率f/Hz相对
变化/%(1, 1) 128.84 133.45 3.45 (1, 2) 240.13 244.18 1.66 (2, 2) 338.86 349.21 2.96 (2, 3) 492.30 497.15 0.98 (3, 3) 633.21 649.39 2.49 (3, 4) 852.42 866.58 1.63 (4, 4) 1 033.10 1 066.80 3.26 (4, 5) 1 289.70 1 303.20 1.04
下载: 导出CSV
-
[1] 陈彦廷, 于昌利, 桂洪斌. 船体板和加筋板的屈曲及极限强度研究综述[J]. 中国舰船研究, 2017, 12(1): 54–62. doi: 10.3969/j.issn.1673-3185.2017.01.009 CHEN Y T, YU C L, GUI H B. Research development of buckling and ultimate strength of hull plate and stiffened panel[J]. Chinese Journal of Ship Research, 2017, 12(1): 54–62 (in Chinese). doi: 10.3969/j.issn.1673-3185.2017.01.009
[2] 程志奎, 赵晨翔. 船体结构振动分析与控制技术[J]. 船舶物资与市场, 2022, 30(1): 58–60. CHENG Z K, ZHAO C X. Hull structure vibration analysis and control technology[J]. Marine Equipment/Materials & Marketing, 2022, 30(1): 58–60 (in Chinese).
[3] XIE K, XU K, DONG W J, et al. An analytic method for vibration analysis of non-uniformly coupled L-shaped plates with arbitrary boundary conditions[J]. Thin-Walled Structures, 2023, 186: 110639. doi: 10.1016/j.tws.2023.110639
[4] CHEN Y H, JIN G Y, ZHU M G, et al. Vibration behaviors of a box-type structure built up by plates and energy transmission through the structure[J]. Journal of Sound and Vibration, 2012, 331(4): 849–867. doi: 10.1016/j.jsv.2011.10.002
[5] ZHANG C Y, JIN G Y, YE T G, et al. Harmonic response analysis of coupled plate structures using the dynamic stiffness method[J]. Thin-Walled Structures, 2018, 127: 402–415. doi: 10.1016/j.tws.2018.02.014
[6] SHAO D, WANG Q S, SHUAI C J, et al. Investigation on dynamic performances of a set of composite laminated plate system under the influences of boundary and coupling conditions[J]. Mechanical Systems and Signal Processing, 2019, 132: 721–747. doi: 10.1016/j.ymssp.2019.07.026
[7] 汤冬, 庞福振, 王青山, 等. 有限尺寸V型薄板功率流透射损失研究[J]. 振动工程学报, 2016, 29(1): 112–122. TANG D, PANG F Z, WANG Q S, et al. Research on transmission loss of power flow through a finite V-shaped plate[J]. Journal of Vibration Engineering, 2016, 29(1): 112–122 (in Chinese).
[8] MARKOSE A, RAO C L. Failure analysis of V-shaped plates under blast loading[J]. Procedia Engineering, 2017, 173: 519–525. doi: 10.1016/j.proeng.2016.12.080
[9] WANG Y, FAN J J, SHEN X, et al. Free vibration analysis of stiffened rectangular plate with cutouts using Nitsche based IGA method[J]. Thin-Walled Structures, 2022, 181: 109975. doi: 10.1016/j.tws.2022.109975
[10] DU Y, JIA D, LI H C, et al. A unified method to analyze free and forced vibration of stiffened plates under various edge conditions[J]. European Journal of Mechanics/A Solids, 2022, 94: 104573. doi: 10.1016/j.euromechsol.2022.104573
[11] SHEN Y J, HE X C, CHEN W, et al. Meshless simulation and experimental study on forced vibration of rectangular stiffened plate[J]. Journal of Sound and Vibration, 2022, 518: 116602. doi: 10.1016/j.jsv.2021.116602
[12] QIN X, SHEN Y J, CHEN W, et al. Bending and free vibration analyses of circular stiffened plates using the FSDT mesh-free method[J]. International Journal of Mechanical Sciences, 2021, 202/203: 106498. doi: 10.1016/j.ijmecsci.2021.106498
[13] PENG L X, CHEN S Y, WEI D Y, et al. Static and free vibration analysis of stiffened FGM plate on elastic foundation based on physical neutral surface and MK method[J]. Composite Structures, 2022, 290: 115482. doi: 10.1016/j.compstruct.2022.115482
[14] TIAN W, ZHAO T, YANG Z C. Theoretical modelling and design of metamaterial stiffened plate for vibration suppression and supersonic flutter[J]. Composite Structures, 2022, 282: 115010. doi: 10.1016/j.compstruct.2021.115010
[15] MAJI P, ROUT M, KARMAKAR A. The thermo-elastic vibration of graphene reinforced composite stiffened plate with general boundary conditions[J]. Structures, 2021, 33: 99–112. doi: 10.1016/j.istruc.2021.04.029
[16] RAJAWAT A S, SHARMA A K, GEHLOT P. Free vibration analysis of Stiffened Laminated Plate using FEM[J]. Materials Today: Proceedings, 2018, 5(2): 5313–5321. doi: 10.1016/j.matpr.2017.12.115
[17] GAO C, PANG F Z, LI H C, et al. A semi-analytical method for the dynamic characteristics of stiffened plate with general boundary conditions[J]. Thin-Walled Structures, 2022, 178: 109513. doi: 10.1016/j.tws.2022.109513
[18] 邢誉峰, 刘波. 板壳自由振动的精确解[M]. 北京: 科学出版社, 2014. XING Y F, LIU B. Exact Solutions of Free Vibrations of Plates and Shells[M]. Beijing: Science Press, 2014 (in Chinese).
[19] 柴玉阳, 杜绍君, 李凤明. 弹性边界约束矩形板的振动特性分析: 理论、有限元和实验[J]. 振动工程学报, 2022, 35(3): 577–584. CHAI Y Y, DU S J, LI F M. Vibration properties of rectangular plates with elastic boundary constraints: theory, finite element and experiments[J]. Journal of Vibration Engineering, 2022, 35(3): 577–584 (in Chinese).
[20] 汤冬, 马梓铜, 张克澳, 等. 正交加筋板中板梁耦合动力特性[J]. 中国舰船研究, 2023, 18(4): 265–275. doi: 10.19693/j.issn.1673-3185.02839 TANG D, MA Z T, ZHANG K A, et al. Dynamic coupling characteristics of the beam and plate components of the orthogonally stiffened plate[J]. Chinese Journal of Ship Research, 2023, 18(4): 265–275 (in Chinese). doi: 10.19693/j.issn.1673-3185.02839
计量
- 文章访问数: 52
- HTML全文浏览量: 1
- PDF下载量: 8
