Vibration and sound radiation analysis of floating raft and hull coupling system based on generalized variational principle
-
摘要:目的
旨在基于广义变分原理研究浮筏−舱段耦合系统的声振特性，提升浮筏隔振系统的声学性能。
方法将浮筏−舱段简化为加筋圆柱壳、双层平板、弹簧及外声场耦合动力学模型。通过广义变分方法构建结构振动能量方程，并基于赫姆霍兹积分方程构建声场域边界元离散方程。采用傅里叶级数和多项式展开的位移与声压，建立半解析声振耦合动力学模型，通过有限元仿真验证模型的准确性。系统研究浮筏和舱段结构多要素对耦合系统的振动声学特性影响规律。
结果所提模型计算结果与有限元分析一致，验证了动力学分析方法的准确性，具有分析效率较高、物理概念清晰的优势。系统研究了隔振器刚度、筏架弹性模态、筏架−设备质量比、舱段结构及肋骨参数等设计要素对耦合系统声学性能的影响规律及优化方法。
结论降低隔振器刚度、提高筏架结构刚度、增大筏架−设备质量比和增大舱段环形肋骨高度可显著提升系统的声学性能。这些结论为浮筏隔振系统的动力学设计、分析及优化设计提供了理论支撑，具有重要的工程应用价值。
Abstract:ObjectiveThis paper investigates the vibro-acoustic characteristics of a floating raft-hull coupling system based on the generalized variational principle, aiming to enhance the acoustic performance of the floating raft vibration isolation system.
MethodsThe floating raft-hull coupling system is simplified into a model consisting of a reinforced cylindrical shell, double-layer plates, springs, and surrounding acoustic medium. The vibration energy equations for the structural domain are derived using the generalized variational method, and the boundary element equations for the acoustic field domain are discretized based on the Helmholtz integral equation. The governing equations of the coupling system are developed by expanding the vibration displacement and acoustic pressure into Fourier series and orthogonal polynomials. The accuracy of the proposed semi-analytical model is validated through finite element method (FEM) simulations.
ResultsThe results show that the proposed model is consistent with FEM analysis, offering high analytical efficiency and clear physical insights. Furthermore, this study systematically investigates the influence laws and optimization methods of various design parameters, including the stiffness of the isolator, the elastic modes of the raft, the raft-to-equipment mass ratio, and the structural parameters of the hull, on the acoustic performance of the coupling system.
ConclusionsIt is concluded that reducing the stiffness of the isolator, increasing the stiffness of the raft structure, increasing the raft-to-equipment mass ratio, and increasing the height of the hull's ring ribs can significantly improve the system's acoustic performance. These conclusions provide theoretical support for the dynamic design, analysis, and optimization of floating raft vibration isolation systems and hold significant value for practical engineering applications.
-
0. 引 言
隔振技术是船舶机械噪声控制的高效手段[1]。船舶隔振技术发展经历了单级隔振、双级隔振和浮筏，并根据应用场景组合应用这3项隔振技术。随着船舶总体振动噪声要求的不断提升，单级隔振和双级隔振逐渐被声学性能更优、资源更节省的浮筏隔振系统取代。因此，浮筏隔振技术成为船舶机械系统噪声控制的重要应用[2]。
浮筏高效隔振源于其质量、混抵和调谐“三个效应”原理[3]，通过两层弹性元件和中间筏架结构，利用弹性波的反射、吸收和衰减降低机械振动向船体结构的传递。为优化提高浮筏隔振系统声学性能，浮筏隔振系统动力学建模与优化分析得到了研究人员广泛的研究和关注。随着浮筏隔振技术的发展，动力学建模分析技术也不断发展，国内外有大量专家学者对其进行了相关研究，提出了包括多体动力学法、子结构综合法、WPA（波传播）法、数值有限元法、半解析法等诸多系统动力学建模分析方法。
多体动力学法将浮筏的上、下层隔振器简化为无质量的弹簧阻尼元件，设备、筏架等部件简化为仅作平动和转动的刚体，忽略了系统内部结构的弹性作用，陈森等[4]基于多刚体动力学方法，建立了复杂空间多刚体系统动力学方程，用于浮筏系统方案设计阶段的振动声学、摇摆与抗冲击计算，该方法分析效率较高，但忽略了系统中部件的弹性，系统声学性能评估分析精度有待提升，特别是高频响应差距较大，局部特性及耦合特性难以掌握。动态子结构分析法包括模态综合法、阻抗/导纳综合法和频响综合法等，这几种方法本质内涵是等价的，黄修长等[5]基于频响函数综合方法，以浮筏基座输入功率流为目标函数，对舱筏隔振系统进行灵敏度分析和优化研究，掌握了隔振元件刚度特性对隔振系统声学的影响规律。该方法便于高效地对连接弹性部件的刚度参数进行灵敏度分析，对于复杂结构或者变化的结构，需要依赖于数值方法重新建模分析获取频响矩阵，分析效率相对较低。WPA法基于弹性波传播视角，分析弹性波在浮筏中的传播、反射和抵消机制。弹性波是振动的内核参数，基于该视角便于更加显性地研究浮筏隔振系统能量传递机理。吴崇建和陈志刚[6]基于WPA法将浮筏视为混合动力系统，建立了系统动力学模型，揭示了浮筏的质量、混抵和调谐“三个效应”的本质机理，该方法适用于机理模型研究，对于复杂结构分析难度相对较大。有限元法在工程结构动力学分析中得到了广泛应用[7]，形成了大量的商用软件。王永远等[8]基于有限元法，研究了浮筏隔振系统设计参数在不同频段对其隔振性能的影响，该方法的优势在于，其可以用于复杂耦合系统的动力学特性精细化分析，但模型前处理和分析效率相对较低，机理分析难度较大。半解析法主要包括各类广义变分法、能量法、近似法等，这些方法主要通过构造系统的能量泛函，对系统进行动力学建模。该类方法既兼具了解析法的计算效率高、蕴含物理信息丰富的优势，又可以建立适当复杂结构动力学分析模型。目前，这类方法发展比较迅速，得到了广泛研究。Qu等[9]基于广义变分法构建圆柱壳与单个弹性薄板的动力学模型，有效预测了耦合系统的结构与声学响应，为弹性系统建模分析提供了思路。He等[10]提出了改进傅里叶级数法，建立不含圆柱壳体的双级平板弹簧动力学模型，分析了系统的振动传递特性。目前，利用相关半解析法、解析法将浮筏与舱段当作一个整体耦合系统，建立浮筏−舱段结构耦合系统动力学模型的研究相对较少。
随着船舶浮筏向“三化”——大型化、集成化、模块化应用的拓展，浮筏隔振系统的声学性能发挥不仅依赖浮筏自身，还需将浮筏与舱段作为耦合统一的整体来研究其声学特性及相关设计参数对系统声学性能的影响机制。考虑到解析方法对复杂耦合系统建模分析难度大，而有限元数值方法研究分析效率低、机理不清晰等问题，本文基于广义变分法建立浮筏−舱段耦合系统的半解析动力学模型，将浮筏与舱段作为一个整体开展相关动力学分析与优化。一方面，提高耦合动力学系统优化分析效率；另一方面，便于开展相关机理分析。所得结果可为浮筏隔振系统动力学分析和声学优化提供支撑。
1. 基于广义变分法的浮筏−舱段耦合系统动力学建模
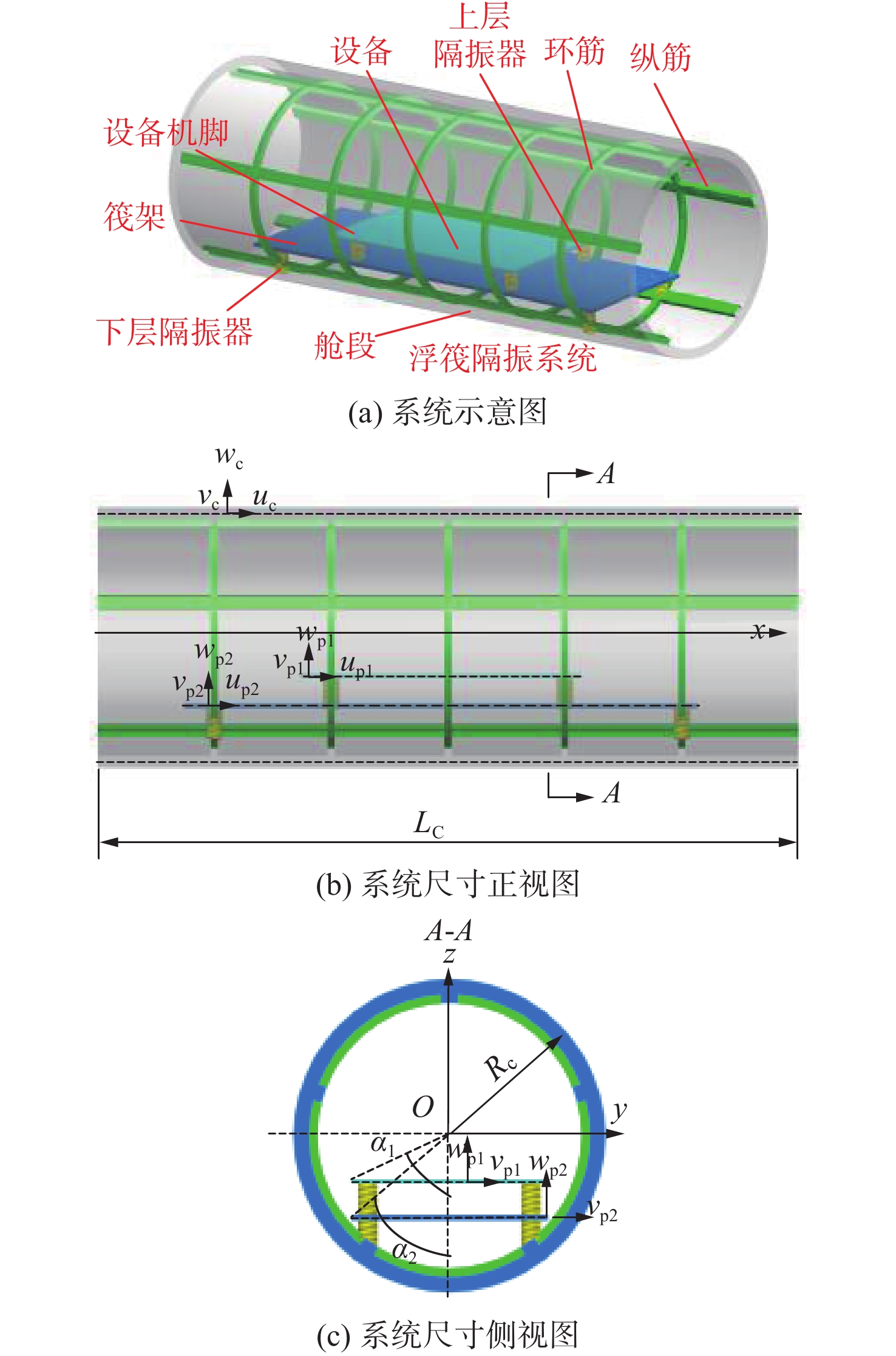
浮筏−舱段耦合系统的简化模型如图1所示。舱段结构简化为正交加筋圆柱壳，浮筏简化为双层弹性支撑连接的平板结构。图中，圆柱壳长度为LC，半径为RC。纵肋和环肋均匀布置，数量为5。设备与筏架、筏架与壳体采用弹簧单元（隔振器）连接。其中，壳体上隔振器连接点在纵横加筋交接点处。设备与筏架相对位置分别用α1和α2来描述。u，v和w分别为圆柱壳纵向、横向和法向位移分量，下标C、p1和p2分别表示艇体、设备和筏架平板的相关参量。
![]()
图 1 浮筏−舱段耦合系统简化模型示意图Figure 1. Schematic of the simplified floating-raft-to-compartment coupled system本文考虑声固耦合，耦合系统的能量函数可以表述为[11]:
Πtol=∫t1t0(ΠC+Πp1+Πp2+Πb+ΠC,p2+Πp1,p2) dt (1) 式中：Π为能量泛函，下标b表示肋的能量泛函；Πp1,p2与ΠC,p2分别为设备与筏架、筏架与艇体间的界面势能泛函。各结构内的能量泛函表示如下：
ΠC=NC∑i=1(TC,i−UC,i+WC,i+WfC,i)+∑i,i+1(ΠC,λκ) (2) Πp1=Np1∑i=1(Tp1,i−Up1,i)+∑i,i+1(Πp1,λκ) (3) Πp2=Np2∑i=1(Tp2,i−Up2,i)+∑i,i+1(Πp2,λκ) (4) Πb=Ns∑m=1(Ts,m−Us,m)+Nr∑k=1(Tr,k−Ur,k) (5) 式中： Ti和Ui分别第i段结构的动能和应变能；Wi为第i段结构外力所做的外功，上标f表示流体做功；Πλκ为相邻壳段的界面势能，下标λ和κ分别为拉格朗日乘子和预设加权参数，κ=1014；对于壳体或者板结构，N为分区数量，对于加强筋， N为加强筋的个数；下标m，k为环肋与纵肋的数量；下标r，s分别表示环肋和纵肋。
圆柱壳的动能、应变能及界面势能表达式为[12]：
TC,i=12(∬ (6) \begin{split} & {U_{{\text{C}},i}} = \Bigg(\iint_{{S_i}} ( {N_x}\varepsilon _x + {N_\theta }\varepsilon _\theta + {N_{x\theta }}\gamma _{x\theta } +\\& {M_x}\chi _x + {M_\theta }\chi _\theta + {M_{x\theta }}\chi _{x\theta } ){R_{\text{C}}}{\text{d}}x{\text{d}}\theta \Bigg)/2 \end{split} (7) \begin{split} & {\varPi _{{\text{C}},\lambda \kappa }} = \int_l ( ( {\lambda _{\text{C}}}{\varTheta _{u,{\text{C}}}} + {\beta _{\text{C}}}{\varTheta _{v,{\text{C}}}} + {\eta _{\rm{C}}}{\varTheta _{w,{\text{C}}}} + {\gamma _{\text{C}}}{\varTheta _{r,{\text{C}}}} ) - \\&\quad\;\; ( {\kappa _u}\varTheta _{u,{\text{C}}}^2 + {\kappa _v}\varTheta _{v,{\text{C}}}^2 + {\kappa _w}\varTheta _{w,{\text{C}}}^2 + {\kappa _r}\varTheta _{r,{\text{C}}}^2 ) ){\text{d}}l {\text{/2}} \end{split} (8) 式中： {S_i} 为圆柱壳体截面面积；\rho 为圆柱壳体密度；l为圆柱壳体长度； {N_x} ， {N_\theta } 和 {N_{x\theta }} 代表单位长度平面内合力； {M_x} ， {M_\theta } 和 {M_{x\theta }} 分别为弯矩和扭矩； \varepsilon _x ， \varepsilon _\theta 和 \gamma _{x\theta } 为应变； \chi _x ， \chi _\theta 和 \chi _{x\theta } 为曲率； {R_{\text{C}}} 为圆柱壳半径； {h_{\text{C}}} 为圆柱壳厚度； {\varTheta _{u,{\text{C}}}} ， {\varTheta _{v,{\text{C}}}} ， {\varTheta _{w,{\text{C}}}} 和 {\varTheta _{r,{\text{C}}}} 是常用界面上的基本连续性方程， {\varTheta _{u,{\text{C}}}} = {u_{i,{\text{C}}}} - {u_{i + 1,{\text{C}}}} ， {\varTheta _{v,{\text{C}}}} = {v_{i,{\text{C}}}} - {v_{i + 1,{\text{C}}}} ， {\varTheta _{w,{\text{C}}}} = {w_{i,{\text{C}}}} - {w_{i + 1,{\text{C}}}} ， {\varTheta _{r,{\text{C}}}} = \partial {w_{i,{\text{C}}}}/\partial x - \partial {w_{i + 1,{\text{C}}}}/ \partial x ； {\lambda _{\rm{C}}} ， {\beta _{\rm{C}}} ， {\eta _{\rm{C}}} 和 {\gamma _{\rm{C}}} 为拉格朗日参数； {\kappa _i}(i = u,v,w,r) 为预分配加权参数，公式详见文献[12]）。
由机械载荷和声场载荷引入的外部做功表示为：
{W_{{\text{C}},i}} = \iint_{{S_i}} {\left( {{f_{u,i}}u_{\text{C}}^i + {f_{v,i}}v_{\text{C}}^i + {f_{w,i}}w_{\text{C}}^i} \right)}{R_{\text{C}}}{\text{d}}x{\text{d}}\theta (9) W_{{\text{C}},i}^{\text{f}} = \iint_{{S_i}} {w_{\text{C}}^ip_{\text{C}}^i{R_{\text{C}}}{\text{d}}x{\text{d}}\theta } (10) 式中：f为机械外力，下标u，v，w分别表示轴向、切向和径向；p表示作用在壳段上的声压。纵肋和环肋的动能及应变能分别为[13]:
\begin{split} & \qquad\;\;{U_{\text{s}}} = \Bigg(\sum\limits_{m = 1}^{{N_{\text{C}}}} \int_{{l_m}} \{ {E_{\text{s}}}[ A_{{\text{s}}m}\varepsilon _{{\text{s}}m,x}^2 + I_{{\text{s}}m,y}\varepsilon _{{\text{s}}m,xx}^2 - \\&\;\; 2I_{{\text{s}}m,y{\textit{z}}}\varepsilon _{{\text{s}}m,xx}\zeta _{{\text{s}}m,xx} + I_{{\text{s}}m,{\textit{z}}}\zeta _{{s} m,xx}^2 - 2A_{{\text{s}}m}d_{sm,0}\varepsilon _{{\text{s}}m,x}\varepsilon _{{\text{s}}m,xx}^2 + \\& 2A_{{\text{s}}m}d_{{\text{s}}m,1}\varepsilon _{{\text{s}}m,xx}^2\zeta _{{\text{s}}m,xx}^2 + \varGamma _{{\text{s}}m}\varepsilon _{{\text{s}}m,xx\theta }^2 ] + G_{{\text{s}}m}J_{{\text{s}}m}\gamma _{x\theta ,{\text{s}}m}^2 \} {\text{d}}x \Bigg)/2 \end{split} (11) \begin{split} & {T_{\text{s}}} = \Bigg({\rho _{\text{s}}}\sum\limits_{j = 1}^{{N_{\text{C}}}} \int_{{l_j}} \{ A_{{\text{s}}j}( {\dot u_{{\text{C}}j}^2 + \dot v_{{\text{C}}j}^2 + \dot w_{{\text{C}}j}^2} ) + I_{{\text{s}}j,y}( {\dot \varphi _{xj}^2 + \dot \varphi _{\theta j}^2} ) + \\&\qquad I_{{\text{s}}j,{\textit{z}}}(\dot \psi _{xj}^2 + \dot \varphi _{\theta j}^2) - 2I_{{\text{s}}j,y{\textit{z}}}{{\dot \varphi }_{xj}}{{\dot \psi }_{xj}} - 2A_{{\text{s}}j}d_{{\text{s}}j,0}{a_{x\theta j,0}} +\\&\qquad\qquad\qquad 2A_{{\text{s}}j}d_{{\text{s}}j,1}{a_{x\theta j,1}} \} {\text{d}}x \Bigg)/2\\[-1pt] \end{split} (12) {U}_{\text{r}}=\frac{1}{2}{\displaystyle {\int }_{{l}_{\text{r}}}{E}_{\text{r},i}({I}_{{\textit{z}}\text{r},i}{\kappa }_{1}^{2}+{I}_{x\text{r},i}{\kappa }_{2}^{2}+{A}_{\text{r},i}{\epsilon }_{s\text{r},i}^{2})\text{d}{l}_{\text{r}}}+\frac{1}{2}{\displaystyle {\int }_{{l}_{\text{r}}}{G}_{\text{r},i}{J}_{\text{r},i}{\gamma }_{\text{r},i}^{2}\text{d}{l}_{\text{r}}} (13) {T_{\text{r}}} = \frac{1}{2}{\rho _{\text{r}}}\int_0^{2{\text{π}} } {\left\{ {A_{\text{r}}\left( {\dot u_{\text{r}}^2 + \dot v_{\text{r}}^2 + \dot w_{\text{r}}^2} \right) + \left( {I_{{\text{r}},x} + I_{{\text{r}},{\textit{z}}}} \right)\dot \varphi _{\text{r}}^2} \right\}R{\text{d}}\theta } (14) 式中： {E_{\text{s}}} ， {E_{{\text{r}},i}} 分别为纵肋、环肋杨氏模量，下标i为结构的分段； {N_{\text{C}}} 为纵肋分段数； {\rho _{\text{s}}} ， {\rho _{\text{r}}} 为纵肋，环肋杨氏模量； A_{{\text{s}}m} ， {A_{{\text{r}},i}} ， I_{{\text{s}}m,i} 和 {I_{{\text{r}},i}} 分别为肋骨的截面积和转动惯量； {\gamma _{{\text{r}},i}} ，和 {\varepsilon _{{\text{s}}r,i}} 为单位长度肋骨的扭角和周向应变； \gamma _{x\theta ,{\text{s}}m} 为纵肋w方向位移相关参数； \varepsilon _{{\text{s}}m,x} 为纵肋u方向位移相关参数； \varepsilon _{{\text{s}}m,xx} 和 \zeta _{{\text{s}}m,xx} 分别为w方向位移相关参数以及v方向位移相关参数； {\kappa _1} 和 {\kappa _2} 为单位长度肋骨的弯曲变化率； {I_{{\textit{z}}{\text{r}},i}} ， {I_{x{\text{r}},i}} 分别为环肋骨截面对截面主轴的弯曲惯性矩； {G_{{\text{r}},i}} 为剪切模量； \varGamma _{{\text{s}}m} 为弯曲扭转常数； \varepsilon _{{\text{s}}m,xx\theta } 为角加速度； d_{{\text{s}}m,0} ， d_{{\text{s}}m,1} ， d_{{\text{s}}j,0} 和 d_{{\text{s}}j,1} 为连接线相对于中心点的位置； \dot \varphi _{xj} ， \dot \varphi _{\theta j} ， \dot \psi _{xj} 和 \dot \varphi _r 为扭转角速度； {J_{{\text{r}},i}} 为环肋骨截面的扭转常数； {a_{x\theta j,0}} ， {a_{x\theta j,1}} 为环形肋骨的科氏加速度；lr为环形肋骨的周向长度， {l_{\text{r}}} = ({R_{\text{C}}} + {h_{r,i}})\theta ( \theta \in [0,{\text{ }}2{\text{π}} ] )，则 {\text{d}}{l_{\text{r}}} = ({R_{\text{C}}} + {h_{r,i}}){\text{d}}\theta ，推导详见文献[13]。
设备的动能和应变能表达如下[14]：
{T_{{\text{p}}1,i}} = \left(\iint_{{S_i}} {{\rho _{{\text{p1}}}}{h_{{\text{p}}1}}(\dot u_{{\text{p}}1}^2 + \dot v_{{\text{p}}1}^2 + \dot w_{{\text{p}}1}^2}){\text{d}}x{\text{d}}y\right)/2 (15) \begin{split} & {U_{{\text{p}}1,i}} = \Bigg(K_{{\text{p}}1}^i\iint_{{S_i}} [ {{( {\dot u_{{\text{p}}1}^i} )}^2} + {{( {\dot v_{{\text{p}}1}^i} )}^2} + 2\mu \dot u_{{\text{p}}1}^i\dot v_{{\text{p}}1}^i +\\& (1 - \mu ){{(\varepsilon _{xy}^{(0)})}^2}/2 ]{\text{d}}x{\text{d}}y\Bigg)/2 + \Bigg(D_{{\text{p}}1}^i\iint_{{S_i}} [ {{( { - \varepsilon _x^1} )}^2} +\\& {{( { - \varepsilon _y^1} )}^2} + 2\mu {\eta _{1,{\text{p}}1}} + (1 - \mu ){{( { - \varepsilon _{xy}^{(1)}} )}^2}/2 ]{\text{d}}x{\text{d}}y\Bigg)/2 \end{split} (16) 式中： K_{{\text{p1}}}^i ， D_{{\text{p1}}}^i 分别为伸展刚度和弯曲刚度；Si为设备面积； \varepsilon _{xy}^{(0)} ， \varepsilon _x^1 ， \varepsilon _y^1 ， \varepsilon _{xy}^{(1)} 和 {\eta _{1,{\text{p}}1}} 为应变分量；μ为结构损失因子； {\rho _{{\text{p1}}}} 为设备结构的材料密度；hp1为设备平板结构的厚度；浮筏架的动能Tp2,i和应变能Up2,i可以参照设备的表达式得到[14]。
对于筏架与圆柱壳体的连接势能：
{\varPi _{{\text{C,p}}2}} = \sum\limits_{s = 1}^{{N_s}} {\left\{ {\left( {{k_{u,s}}\varTheta _u^2 + {k_{v,s}}\varTheta _v^2 + {k_{w,s}}\varTheta _w^2} \right)/2} \right\}} (17) \begin{split} & {\varTheta _u} = {u_{{\text{p}}2}} - {u_{\text{C}}},{\varTheta _v} = {v_{{\text{p}}2}} - {{\tilde v}_{\text{C}}},{\varTheta _w} = {w_{{\text{p}}2}} - {{\tilde w}_{\text{C}}}, \\&\;\;\;\;\;\; {\varTheta _r} = \partial {w_{{\text{p}}1}}/\partial y - \left( {\partial {w_{\text{C}}}/\partial \theta - {v_{\text{C}}}} \right)/{R_{\text{C}}} \\&\qquad {{\tilde v}_{\text{C}}} = {A_1}\cos {\alpha _1}{v_{\text{C}}} + {A_2}\sin {\alpha _1}{w_{\text{C}}}, \\&\qquad {{\tilde w}_{\text{C}}} = {A_3}\sin {\alpha _1}{v_{\text{C}}} + {A_4}\cos {\alpha _1}{w_{\text{C}}} \end{split} (18) 式中，k为弹簧刚度；Ns为弹簧数量；[A1, A2, A3, A4] 分别为浮筏与壳体界面接触左侧和接触右侧上的位移系数，对于左侧接触系数为 [−1, −1, 1, −1]，对于右侧接触系数则为[1, −1, −1, −1]。
对于筏架和设备之间的连接势能：
{\varPi _{{\text{p1,p2}}}} = \sum\limits_{s = 1}^{{N_s}} {\left\{ {\left( {{k_{u,s}}\varTheta _u^2 + {k_{v,s}}\varTheta _v^2 + {k_{w,s}}\varTheta _w^2} \right)/2} \right\}} (19) {\varTheta _u} = {u_{{\text{p}}1}} - {u_{{\text{p}}2}},{\varTheta _v} = {v_{{p} 1}} - {v_{{\text{p}}2}},{\varTheta _w} = {w_{{\text{p}}1}} - {w_{{\text{p}}2}} (20) 基于圆柱壳为轴对称结构，故沿周向和轴向分别用傅里叶级数和正交多项式进行位移扩展。筏架和设备位移函数沿长宽两个方向用正交多项式展开，本论文中采用切比雪夫正交多项式，则浮筏−舱段系统的位移可表示为：
\begin{split} & {u_{\rm{C}}}( {x,\theta ,t} ) = \sum\limits_{m = 1}^{{Q_{\rm{C}}}} \sum\limits_{n = 0}^{{P_{\rm{C}}}} {T_m}( x )[ \sin ( {n\theta } )u_{C,mn}^{\text{s}}( t ) +\\&\quad\quad \cos ( {n\theta } )u_{C,mn}^{\text{c}}( t ) ] = {{\boldsymbol{U}}_{\rm{C}}}( {x,\theta } ){{\boldsymbol{u}}_{\rm{C}}}( t ) \\& {v_{\rm{C}}}( {x,\theta ,t} ) = \sum\limits_{m = 1}^{{Q_{\rm{C}}}} \sum\limits_{n = 0}^{{P_{\rm{C}}}} {T_m}( x )[ \sin ( {n\theta } )v_{C,mn}^{\text{c}}( t ) + \\&\quad\quad \cos ( {n\theta } )v_{C,mn}^{\text{s}}( t ) ] = {{\boldsymbol{V}}_{\rm{C}}}( {x,\theta } ){{\boldsymbol{v}}_{\rm{C}}}( t ) \\& {w_{\rm{C}}}( {x,\theta ,t} ) = \sum\limits_{m = 1}^{{Q_{\rm{C}}}} \sum\limits_{n = 0}^{{P_{\rm{C}}}} {T_m}( x )[ \sin ( {n\theta } )w_{C,mn}^{\text{s}}( t ) +\\&\quad\quad \cos ( {n\theta } )w_{C,mn}^{\text{c}}( t ) ] = {{\boldsymbol{W}}_{\rm{C}}}( {x,\theta } ){{\boldsymbol{w}}_{\rm{C}}}( t ) \end{split} (21) {u_{{\text{p}}1}}\left( {x,y,t} \right) = \sum\limits_{m = 1}^{{Q_{{\text{p}}1}}} {\sum\limits_{n = 0}^{{P_{{\text{p}}1}}} {{T_m}\left( x \right){T_n}\left( y \right){u_{{\text{p}}1,mn}}} } = {{\boldsymbol{U}}_{{\text{p}}1}}\left( {x,y} \right){{\boldsymbol{u}}_{{\text{p}}1}}\left( t \right) \begin{gathered} {v_{{\text{p}}1}}\left( {x,y,t} \right) = \sum\limits_{m = 1}^{{Q_{{\text{p}}1}}} {\sum\limits_{n = 0}^{{P_{{\text{p}}1}}} {{T_m}\left( x \right){T_n}\left( y \right){v_{{\text{p}}1,mn}}} } = {{\boldsymbol{V}}_{{\text{p}}1}}\left( {x,y} \right){{\boldsymbol{v}}_{{\text{p}}1}}\left( t \right) \\ {w_{{\text{p}}1}}\left( {x,y,t} \right) = \sum\limits_{m = 1}^{{Q_{{\text{p}}1}}} {\sum\limits_{n = 0}^{{P_{{\text{p}}1}}} {{T_m}\left( x \right){T_n}\left( y \right){w_{{\text{p}}1,mn}}} } = {{\boldsymbol{W}}_{{\text{p}}1}}\left( {x,y} \right){{\boldsymbol{w}}_{{\text{p}}1}}\left( t \right) \\ \end{gathered} (22) \begin{gathered} {u_{{\text{p}}2}}\left( {x,y,t} \right) = \sum\limits_{m = 1}^{{Q_{{\text{p}}2}}} {\sum\limits_{n = 0}^{{P_{{\text{p}}2}}} {{T_m}\left( x \right){T_n}\left( y \right){u_{{\text{p}}2,mn}}} } = {{\boldsymbol{U}}_{{\text{p}}2}}\left( {x,y} \right){{\boldsymbol{u}}_{{\text{p}}2}}\left( t \right) \\ {v_{{\text{p}}2}}\left( {x,y,t} \right) = \sum\limits_{m = 1}^{{Q_{{\text{p}}2}}} {\sum\limits_{n = 0}^{{P_{{\text{p}}2}}} {{T_m}\left( x \right){T_n}\left( y \right){v_{{\text{p}}2,mn}}} } = {{\boldsymbol{V}}_{{\text{p}}2}}\left( {x,y} \right){{\boldsymbol{v}}_{{\text{p}}2}}\left( t \right) \\ {w_{{\text{p}}2}}\left( {x,y,t} \right) = \sum\limits_{m = 1}^{{Q_{{\text{p}}2}}} {\sum\limits_{n = 0}^{{P_{{\text{p}}2}}} {{T_m}\left( x \right){T_n}\left( y \right){w_{{\text{p}}2,mn}}} } = {{\boldsymbol{W}}_{{\text{p}}2}}\left( {x,y} \right){{\boldsymbol{w}}_{{\text{p}}2}}\left( t \right) \\ \end{gathered} (23) 式中，Q和P表示傅里叶级数和多项式的截断阶数；U，V和W为位移函数向量；u，v和w为广义位移向量；Ti为第i阶正交多项式，本文中Ti采用切比雪夫正交多项式；上标c和s表示轴对称和反对称位移分量。
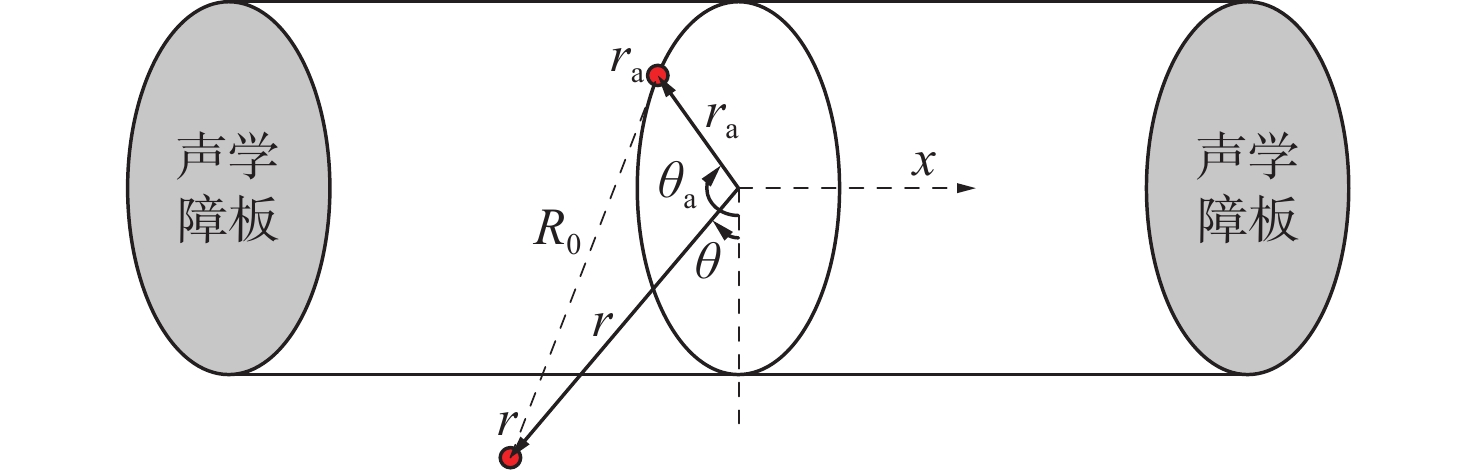
声学模型由壳体−流体−声障板组成，如图2所示。采用柱坐标(r, θ, x)来描述模型，坐标原点位于圆柱壳的中心。壳−流体界面沿轴向划分为NC段，声障板沿径向分为NB段。
柱坐标系下的Kirchhoff−Helmoholtz积分方程为[15]：
\begin{split} & C({\boldsymbol{r}})p({\boldsymbol{r}}) = \iint_{{S_{\text{a}}}} [ p( {{{\boldsymbol{r}}_{\text{a}}}} )\partial G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )/\partial {{\boldsymbol{n}}_{\text{a}}} -\\&\qquad G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )\partial p( {{{\boldsymbol{r}}_{\text{a}}}} )/\partial {{\boldsymbol{n}}_{\text{a}}} ]{\text{d}}S \end{split} (24) 式中：r(r, θ, x)和ra(ra, θa, xa)分别为源点和场点；p (r)和p (ra)分别为源点和场点的压力；na表示点ra处的单位向量向外法线；Sa表示声场边界，包括壳流耦合界面和两个声障板；系数C(r)与源点r的位置有关，C(r)在流体外部等于0，在流体内部等于1，在Sa表面上设为0.5；G(r, ra)是自由空间Green函数。Green函数如下[15]：
\begin{split} & G\left( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} \right) = {{\mathrm{e}}^{ - ik{R_0}}}/4{\text{π}} {R_0} \\& {R_0} = \left| {{\boldsymbol{r}} - {{\boldsymbol{r}}_{\text{a}}}} \right| = \sqrt {{r^2} + r_{\text{a}}^2 - 2r{r_{\text{a}}}\cos \left( {\theta - {\theta _{\text{a}}}} \right) + {{\left( {x - {x_{\text{a}}}} \right)}^2}} \end{split} (25) 式中，k=ω/cf，为声波波数，其中ω和cf分别为角频率和声速。当声源点在声障板上时，压力对na的偏导数等于0，在壳−流体界面上可表示为[15]：
\partial p({{\boldsymbol{r}}_0})/\partial p({{\boldsymbol{n}}_0}) = {\rho _{\text{f}}}{\omega ^2}{{{w}}_{\text{C}}} = {\rho _{\text{f}}}{\omega ^2}{{\boldsymbol{W}}_{\text{C}}}{{\boldsymbol{w}}_{\text{C}}} (26) 式中， {{\boldsymbol{r}}_0} 为声障板上的点； {{\boldsymbol{n}}_0} 为点 {{\boldsymbol{r}}_0} 处的单位向量向外法线；ρf 表示声介质密度。
声压在周向和轴向分别用傅里叶级数和正交多项式展开，可得:
p({\boldsymbol{r}}) = \sum\limits_{m = 0}^{{Q_{\text{p}}} - 1} {\sum\limits_{n = 0}^{{P_{\text{p}}}} {{\chi _m}\left( {\boldsymbol{x}} \right)\left[ {p_n^{\text{s}}\sin \left( {n\theta } \right) + p_n^{\text{c}}\cos \left( {n\theta } \right)} \right]} } = {{\boldsymbol{P}}_{\text{p}}}\left( {x,\theta } \right){\boldsymbol{p}} (27) 式中： Qp和Pp分别为多项式和傅立叶级数的截断阶数；p为广义压力矢量；Pp为混合函数向量； {\chi _m} 为多项式的阶数；x为壳体轴向坐标，挡板径向坐标。
将方程(21)～方程(23)代入方程(24)，推导出积分并表述为:
\begin{split} & C\left( {\boldsymbol{r}} \right)p\left( {\boldsymbol{r}} \right) = \sum\limits_{q = 1}^{{N_{\text{t}}}} {\iint_{{S_{{\text{a}},q}}} {\left[ {(\partial G\left( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} \right)/\partial {{\boldsymbol{n}}_{\text{a}}}){{\boldsymbol{P}}_{\text{p}}}{{\boldsymbol{r}}_0}{\text{d}}x{\text{d}}\theta } \right]{\boldsymbol{p}}}} - \\&\qquad\qquad \sum\limits_{q = 1}^{{N_{\text{L}}}} {\iint_{{S_{\text{a}}}} {\left[ {{\rho _{\text{f}}}{\omega ^2}G\left( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} \right)R{\text{d}}x{\text{d}}\theta } \right]{{\boldsymbol{w}}_{\text{C}}}}} \\[-1pt] \end{split} (28) 式中：Nt为声边界段数，即NC+2NB。对Green函数进行傅里叶级数展开，则Green函数及其法向导数可表示为:
\begin{split} & \quad\quad G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} ) = \sum\limits_{n = 0}^{{n_{\text{G}}}} [ G_n^{\text{s}}( {r,{\textit{z}},{r_{\text{a}}},{{\textit{z}}_{\text{a}}}} )\sin ( {n{\theta _{\text{a}}}} ) + \\&\qquad\quad\quad G_n^{\text{c}}( {r,{\textit{z}},{r_{\text{a}}},{{\textit{z}}_{\text{a}}}} )\cos ( {n{\theta _{\text{a}}}} ) ] \\&\;\; \partial G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )/\partial {{\boldsymbol{n}}_{\text{a}}} = \sum\limits_{n = 0}^{{n_{\text{G}}}} [ \bar G_n^{\text{s}}( {r,{\textit{z}},{r_{\text{a}}},{{\textit{z}}_{\text{a}}}} )\sin ( {n{\theta _{\text{a}}}} ) + \\&\qquad\quad\quad \bar G_n^{\text{c}}( {r,{\textit{z}},{r_{\text{a}}},{{\textit{z}}_{\text{a}}}} )\cos ( {n{\theta _{\text{a}}}} ) ] \\&\quad\;\; G_n^{\text{s}} = \Bigg(\int_0^{2{\text{π}} } G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )\sin ( {n{\theta _{\text{a}}}} ) {\text{d}}{\theta _{\text{a}}},G_n^{\text{c}}\Bigg)/{\text{π}} =\\&\qquad\quad\quad \Bigg(\int_0^{2{\text{π}} } {G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )\cos ( {n{\theta _{\text{a}}}} )} {\text{d}}{\theta _{\text{a}}}\Bigg)/{\text{π}} \\& \bar G_n^{\text{s}} = \Bigg(\int_0^{2{\text{π}} } {(\partial G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )/\partial {{\boldsymbol{n}}_{\text{a}}})\sin ( {n{\theta _{\text{a}}}} )} {\text{d}}{\theta _{\text{a}}},\bar G_n^{\text{c}}\Bigg)/{\text{π}} =\\&\qquad\quad \Bigg(\int_0^{2{\text{π}} } {(\partial G( {{\boldsymbol{r}},{{\boldsymbol{r}}_{\text{a}}}} )/\partial {{\boldsymbol{n}}_{\text{a}}})\cos ( {n{\theta _{\text{a}}}} )} {\text{d}}{\theta _{\text{a}}}\Bigg)/{\text{π}} \end{split} (29) 式中： G_n^{\text{s}} 为格林函数的周向展开波数正弦部分； G_n^{\text{c}} 为格林函数的周向展开波数余弦部分； \bar G_n^{\text{s}} 为格林函数的法向导数周向展开波数的正弦部分； \bar G_n^{\text{c}} 为格林函数的法向导数周向展开波数的余弦部分；nG为周向波数最大截断阶数。将方程(29)代入方程(28)，将积分公式转化为一维问题，然后采用配点法对积分方程进行离散化。选取切比雪夫多项式的根作为声学边界上的配点，每个边界段上的积分点个数设为Qa。此外，采用CHIEF方法（combined Helmholtz integral equation formalism）避免了积分方程的奇异性。本文选取了流体外的一个CHIEF点。因此，离散积分方程可表述为：
{\boldsymbol{Hp}} = {\boldsymbol{Gw}} (30) 式中，H和G是系数矩阵。
考虑壳−流体相互作用。将方程(1)、方程(27)、方程(30)代入方程(10)，流体载荷对外做功改写为：
W_{{\text{C}},i}^{\text{f}} = {{\boldsymbol{q}}^{\text{T}}}{{\boldsymbol{T}}^{\text{T}}}\left[ {\iint_{{S_i}} {{\boldsymbol{W}}_{\text{C}}^i{\boldsymbol{P}}_{\text{C}}^i{R_{\text{C}}}{\text{d}}x{\text{d}}\theta }} \right]{{\boldsymbol{H}}^ - }{\boldsymbol{GTq}} (31) 式中，H−为H的逆矩阵运算；T为转换矩阵，将壳体法向位移扩展为系统全部结构位移组装的广义位移向量q。将方程(21)～方程（23）和方程（31）代入方程(1)，运用变分原理，可得控制方程为：
\left( {{{\boldsymbol{K}}_{\text{s}}} - {\omega ^2}{{\boldsymbol{M}}_{\text{s}}} + {{\boldsymbol{H}}_{\text{f}}}} \right){\boldsymbol{q}} = {{\boldsymbol{F}}_{\text{s}}} (32) 式中：Ks和Ms分别为结构刚度矩阵和质量矩阵；Hf为流体加载引入的矩阵；Fs为由外部激励引入的广义力矢量。相关矩阵推导思路详见文献[13]。
2. 浮筏−舱段耦合系统动力学建模仿真验证
为验证基于广义变分原理建立的浮筏−舱段耦合系统动力学模型的准确性，选择一个浮筏−舱段模型进行仿真验证。该模型包含了壳体、筏架等主要结构部件。其中，壳体长度
3000 mm，半径500 mm，板厚3 mm，内部用环筋和纵筋加强。环筋尺寸30 mm×30 mm，纵筋尺寸30 mm×40 mm。筏架简化为尺寸2 000 mm×500 m、厚度8 mm的平板，质量60 kg，结构材料密度7 500 kg/m³。设备简化为尺寸为1 000 mm×500 mm、厚度7.5 mm的平板，质量为30 kg，结构材料密度为8 000 kg/m3。舱段、模拟设备、筏架等结构的阻尼均采用结构阻尼模拟，结构阻尼系数取为0.01，泊松比均为0.3。在基准算例中，上层隔振器安装频率取8 Hz，单个弹簧的刚度k1为18 950 N/m；下层隔振器安装频率取4 Hz，单个弹簧的刚度k2为
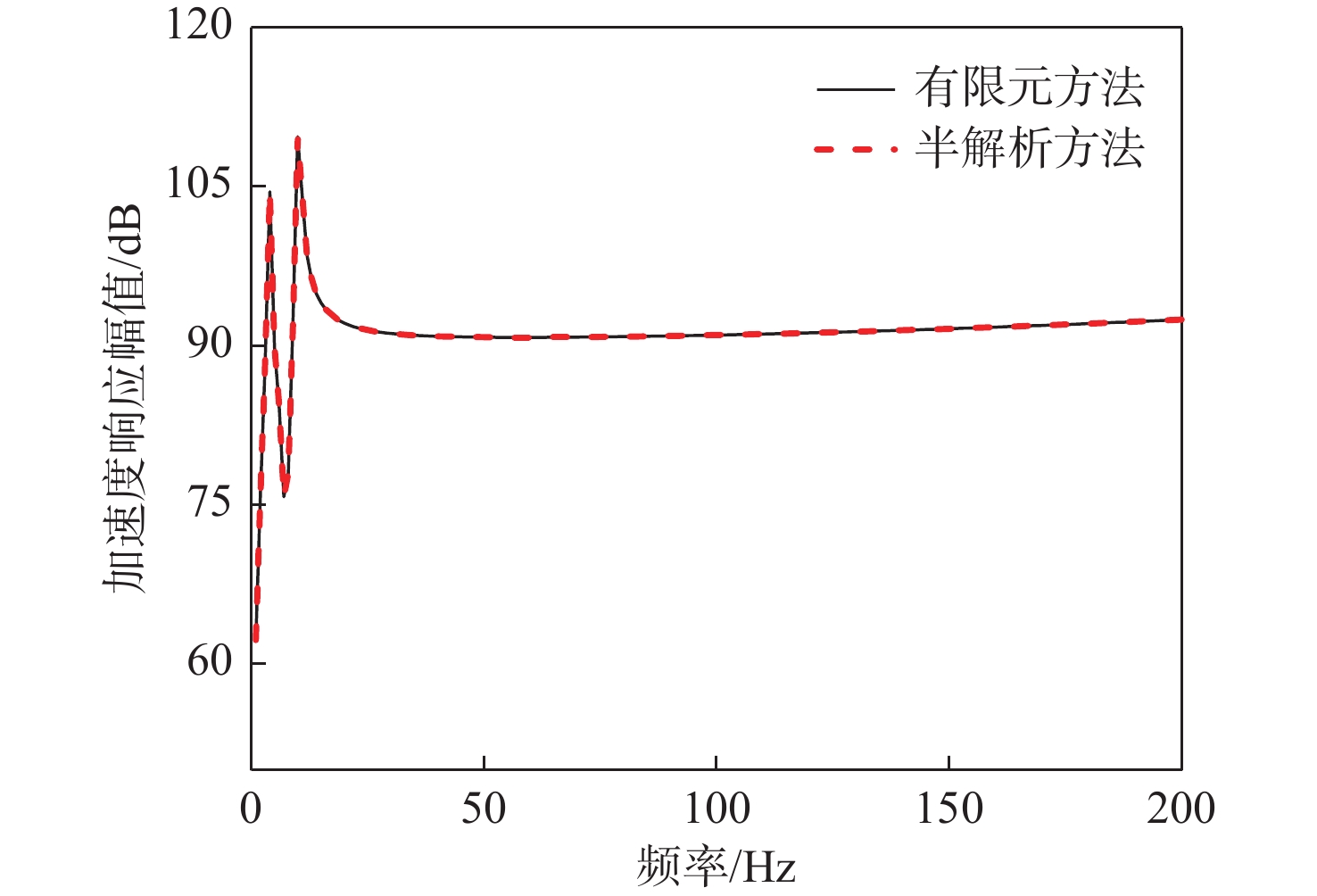
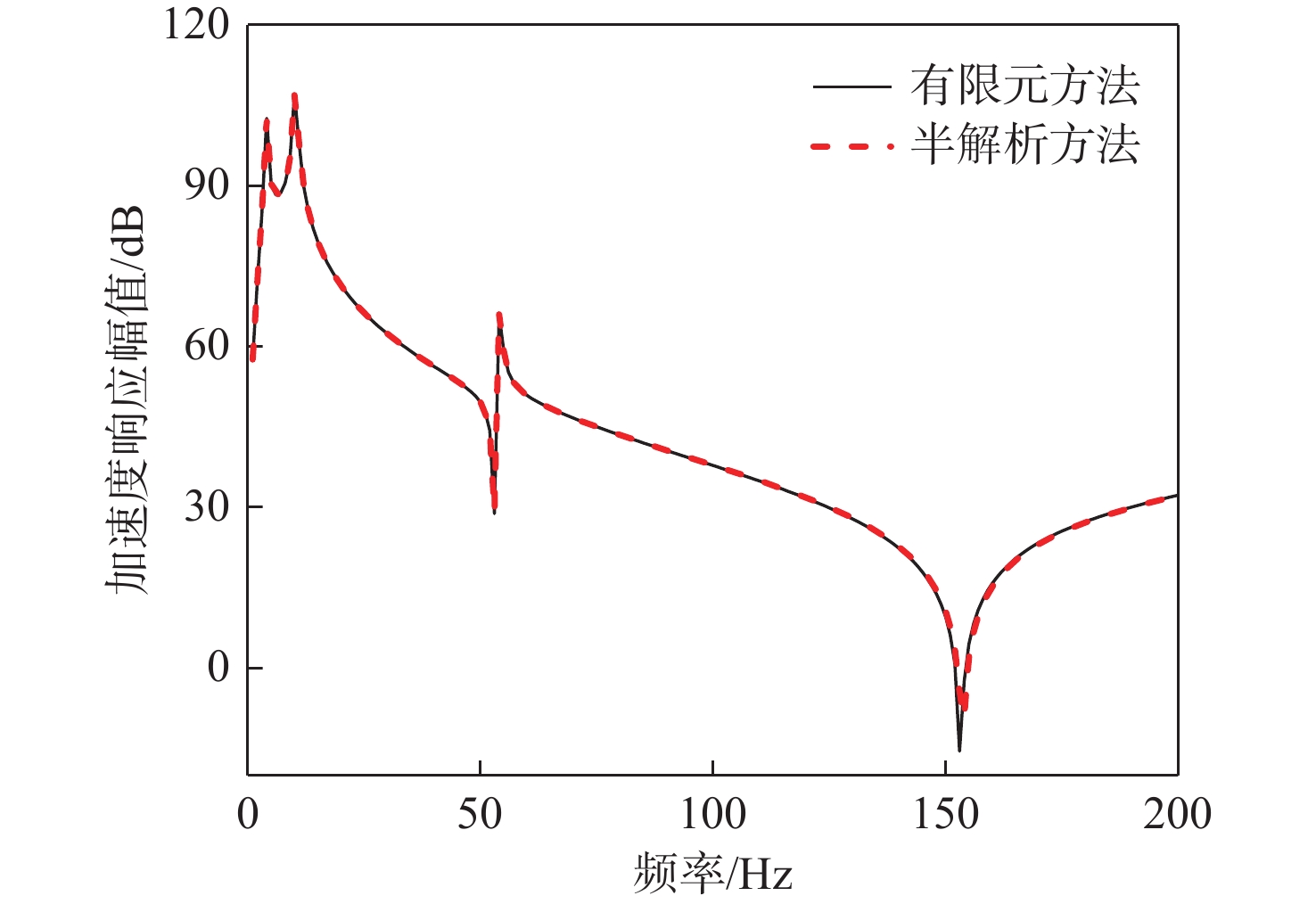
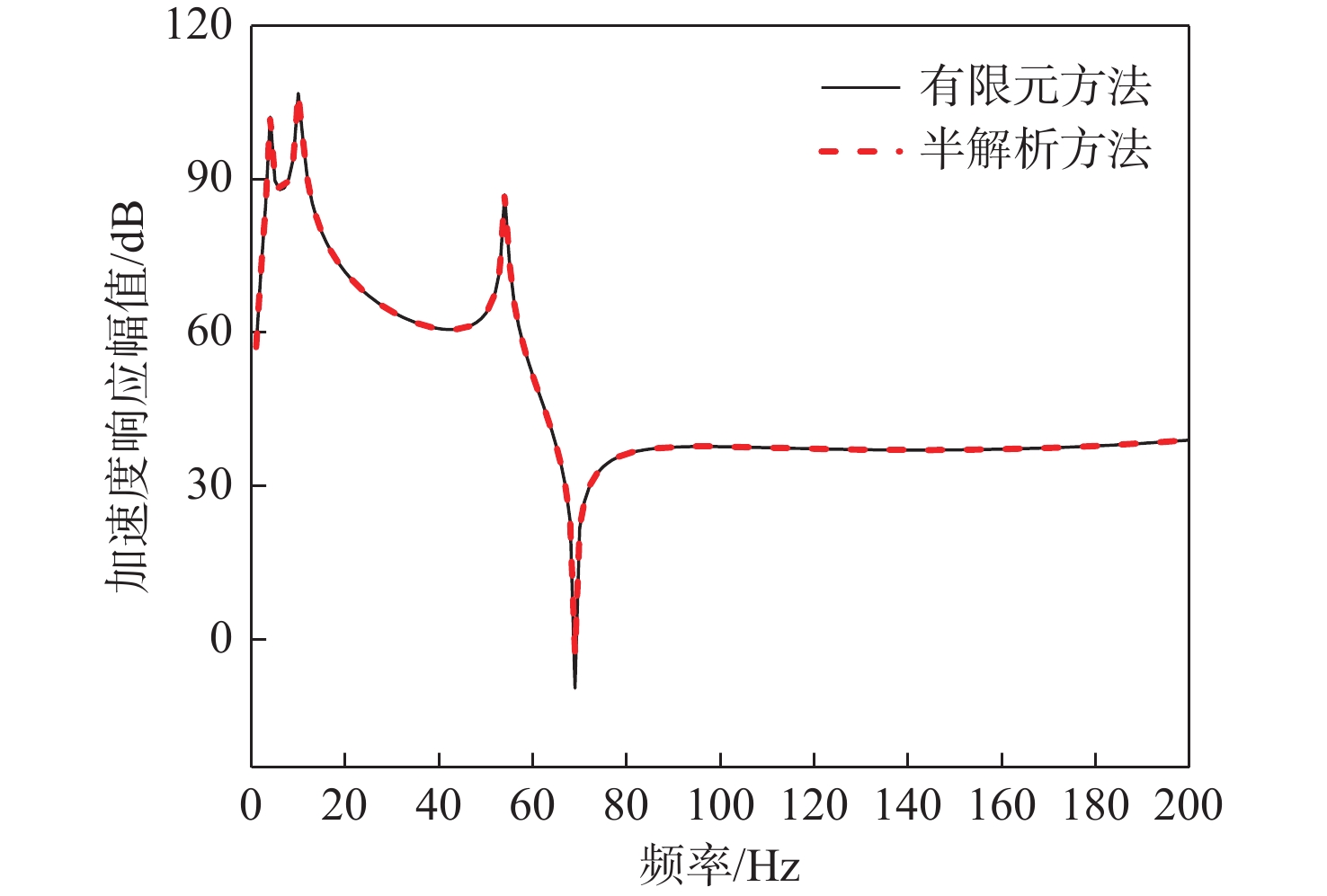
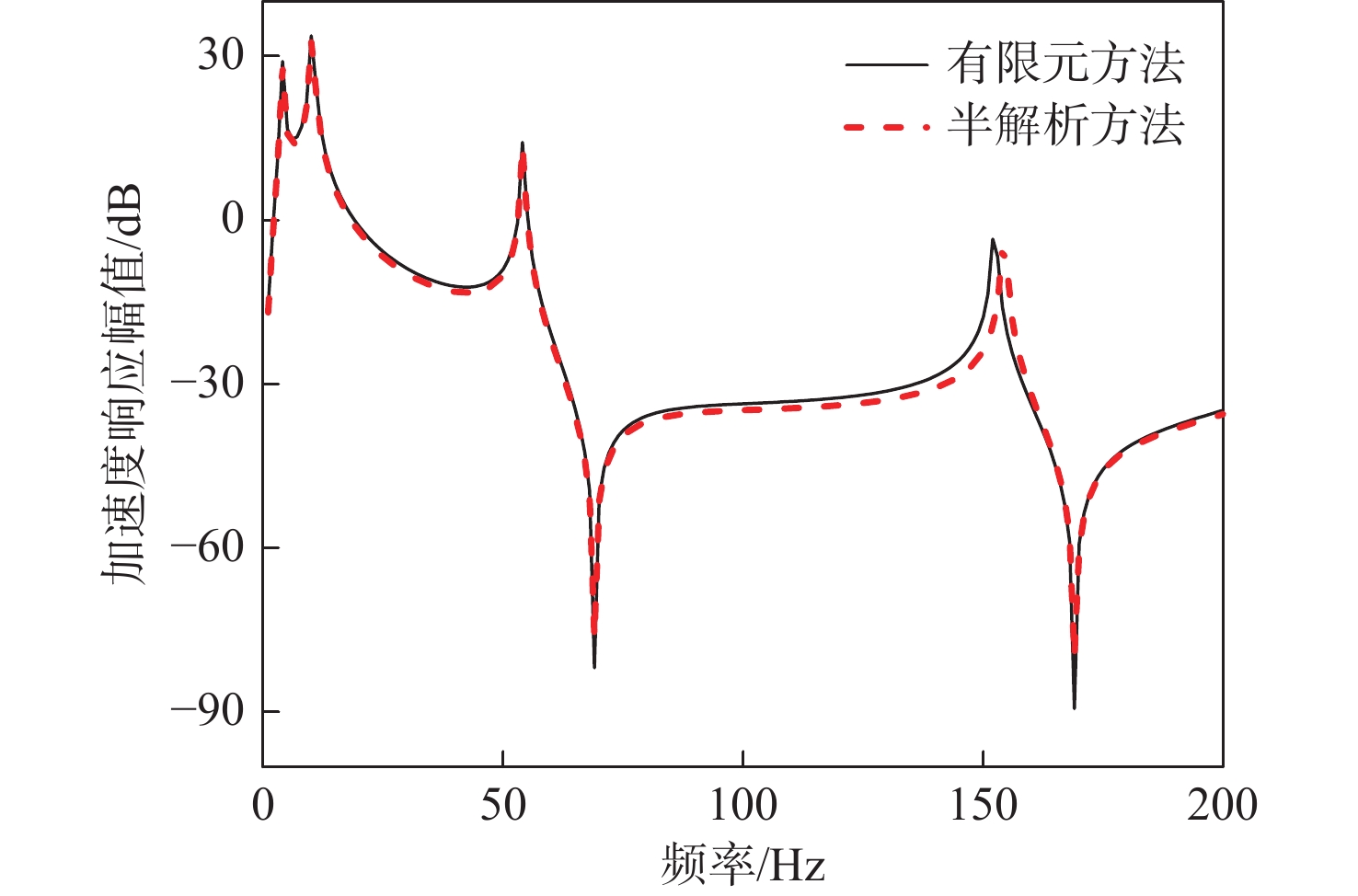
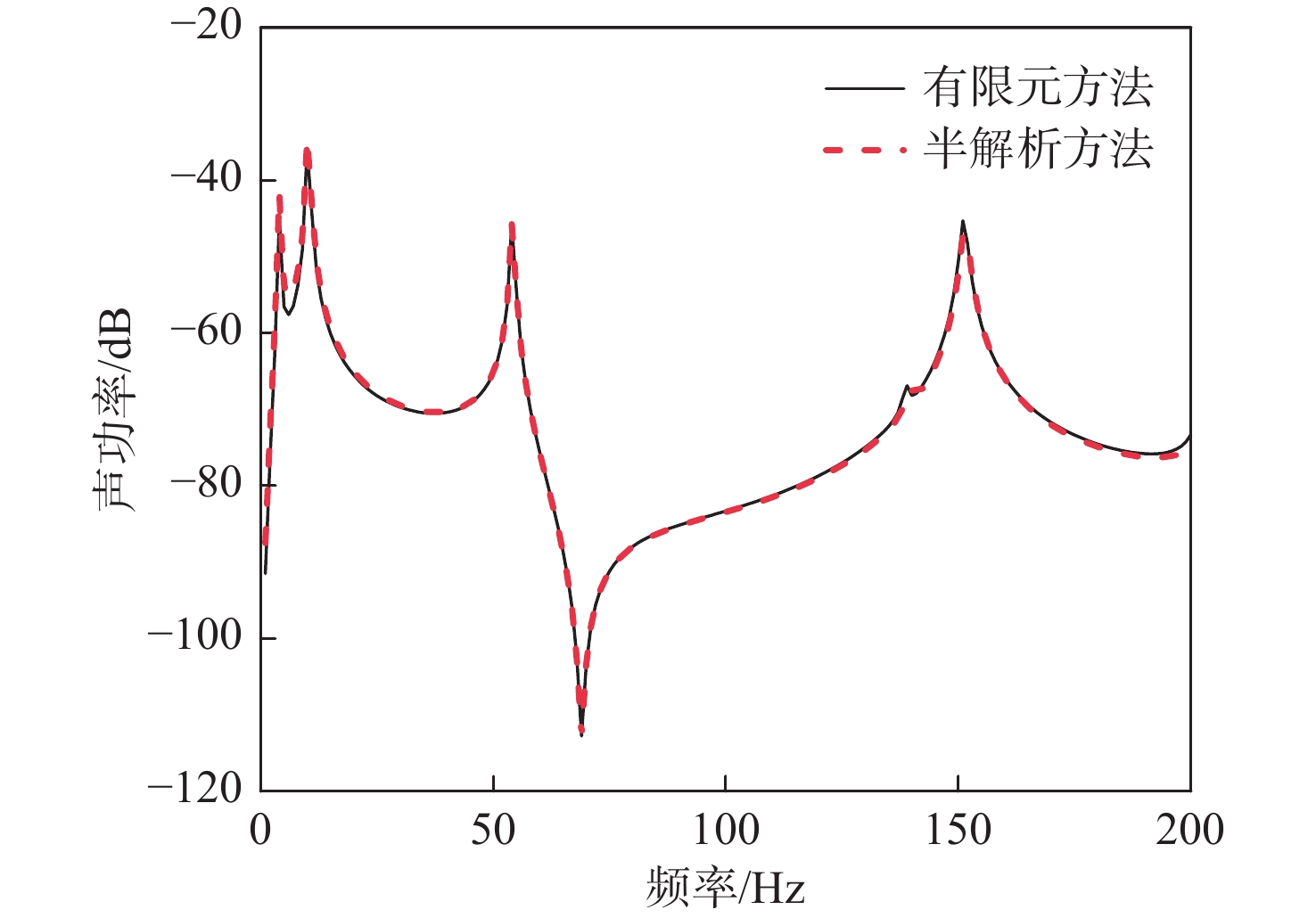
14212 N/m。隔振器的阻尼采用结构阻尼模拟，阻尼系数均取为0.01。设备简化为刚体平板，弹性模量5×1013 Pa；筏架弹性模量5×1012 Pa，壳体弹性模量5×1011 Pa。筏架和舱段壳体采用壳单元模拟，环筋与纵筋采用梁单元模拟，上、下层隔振器采用弹簧单元模拟。在验证过程中，圆柱壳两端采用简支边界，在设备质心处施加垂向单位激励力。计算并分析系统典型结构部位（典型结构部位已在图1中标注）的振动响应和声辐射特性，计算结果表明，基于广义变分法的动力模型与有限元分析一致，如图3～图8所示，验证了所提动力学建模方法的可行性和准确性。值得说明的是，为了便于研究系统动力学特性机理、规律，本节对浮筏−舱段耦合系统结构参数进行了简化，相关结构参数以及激励源与实际工程参数存在差异，因此相关研究机理、规律可以借鉴，幅值大小仅供参考。
![]()
图 5 筏架结构上层隔振器安装点振级Figure 5. Vibration level at upper isolator installation points of raft structure![]()
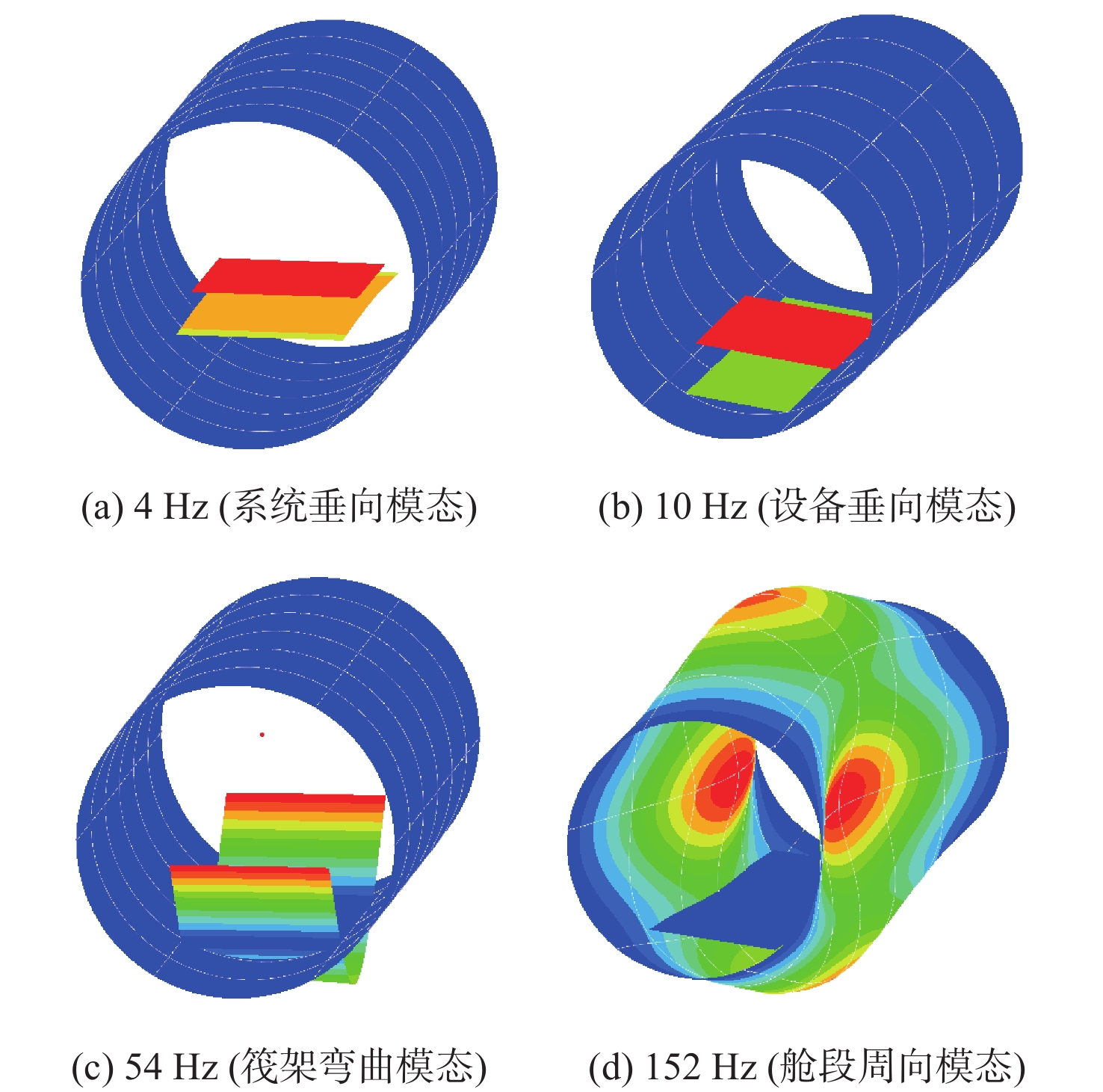
图 6 筏架结构下层隔振器安装点振级Figure 6. Vibration level at lower isolator installation points of raft structure进一步分析系统响应的特征峰值对应的系统模态，如图9所示，浮筏系统响应曲线主要有4 个特征峰值频率，4和10 Hz 为隔振系统前2阶垂向模态频率，54 Hz为筏架一阶弯曲模态，152 Hz为舱段壳体n=2时的一阶周向模态。值得注意的是，舱段结构的模态振动特征频率会在基座振级和系统声辐射特性曲线中出现，其它评价参数包括动态力传递率、设备振级、筏架振级等均无该振动模态峰值特征。
3. 系统振动传递特性分析
3.1 上层隔振器的影响
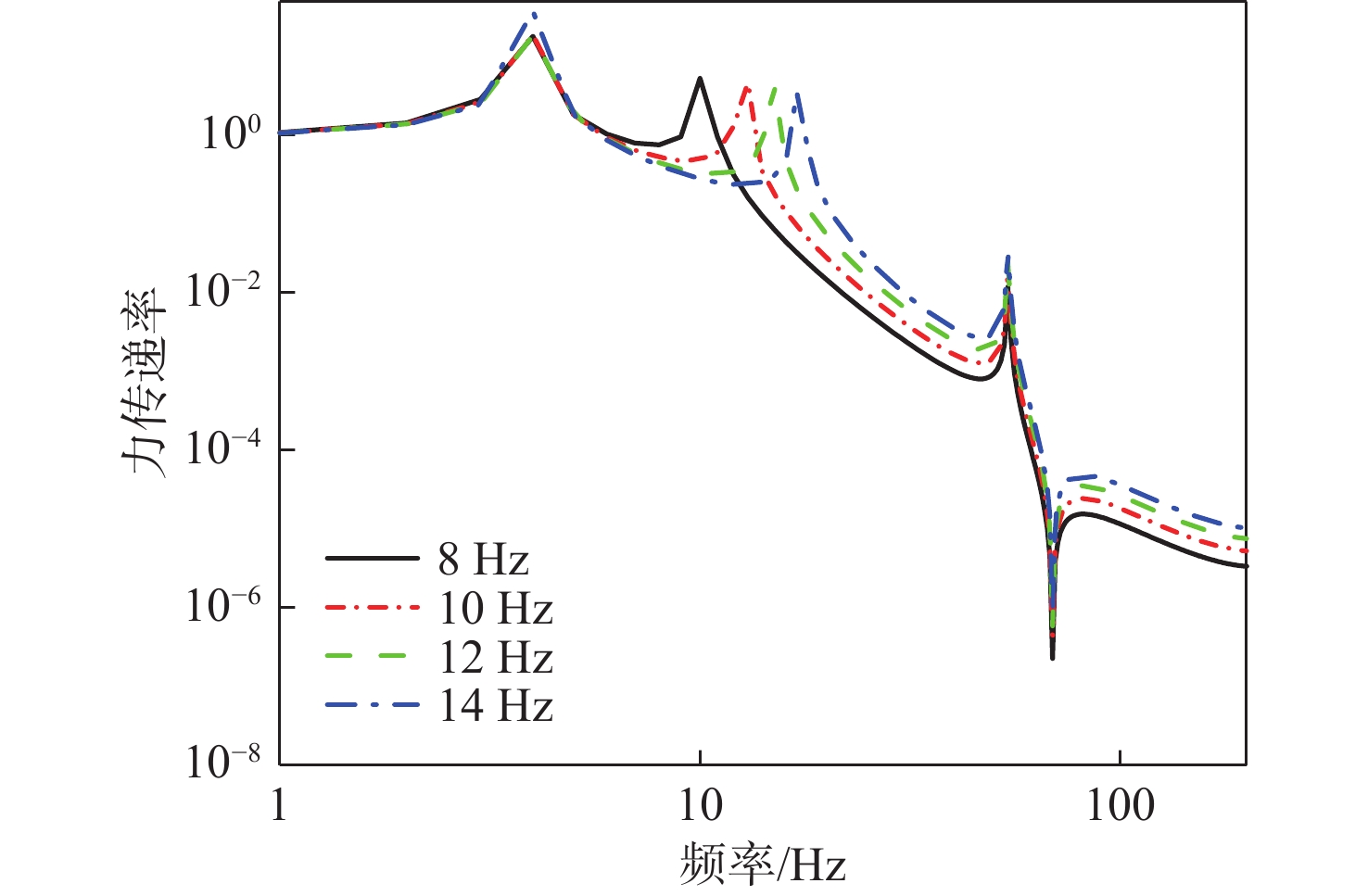
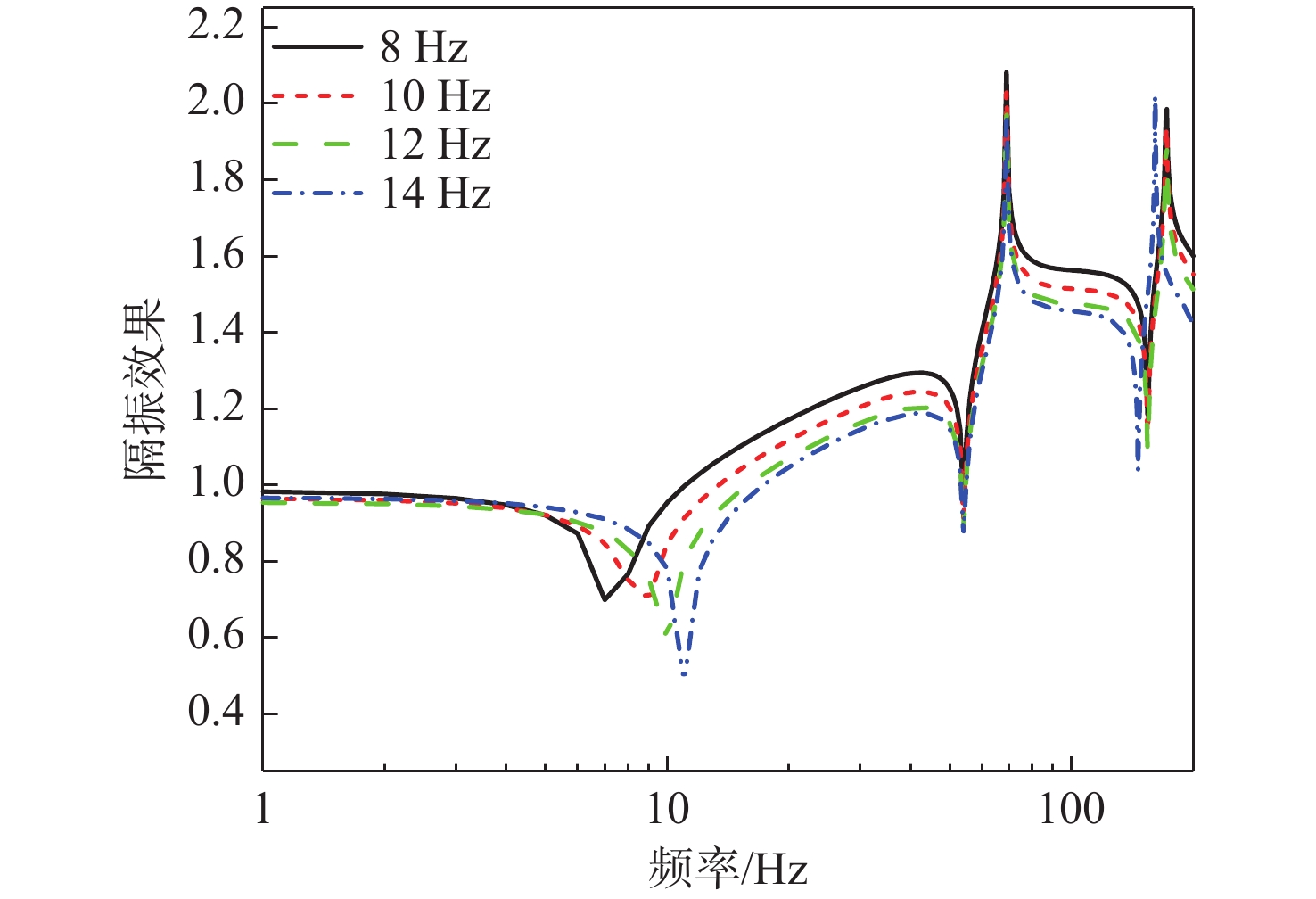
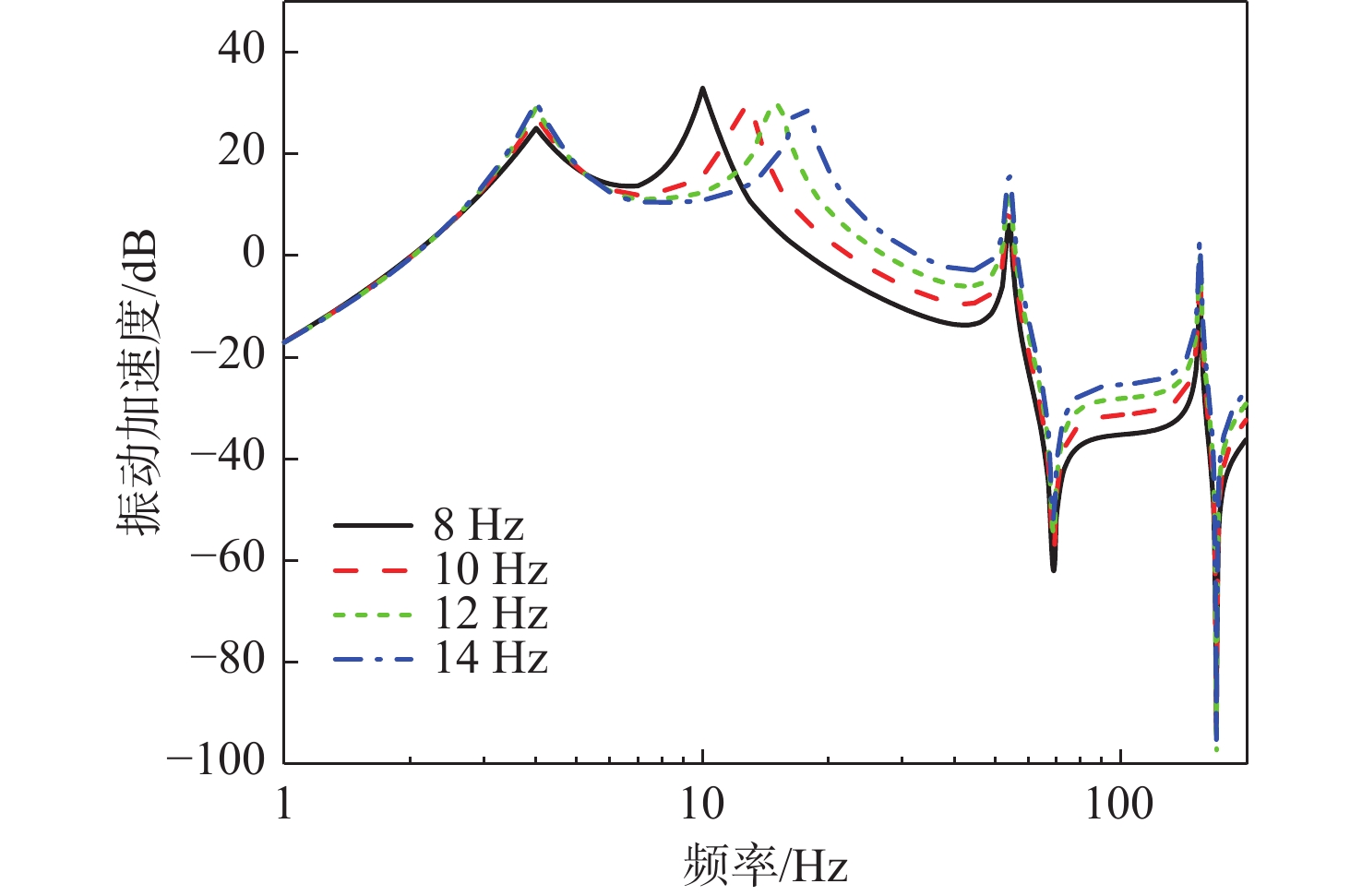
基于该模型，研究上层隔振器刚度对系统振动传递特性的影响。保持其他设计要素与基准算例一致，改变上层隔振器刚度k1，使上层设备安装频率分别取8，10，12，14 Hz，计算得到浮筏−舱段耦合系统的动态力传递、隔振效果（本文中隔振效果为归一化处理后的结果，后面均进行了归一化处理）和舱段基座振动加速度级，结果如图10～图12所示。可以看出：
![]()
图 10 上层隔振器刚度变化对力传递率的影响Figure 10. Effect of upper isolator stiffness variation on force transmissibility![]()
图 11 上层隔振器刚度变化对隔振效果的影响Figure 11. Effect of upper isolator stiffness variation on force transmissibility![]()
图 12 上层隔振器刚度对基座振级的影响Figure 12. Effect of upper isolator stiffness on pedestal vibration level1） 动态力传递率曲线有3个峰值点，前2个峰值频率对应浮筏隔振系统前2垂向模态，第3个峰值频率对应筏架的弹性模态；
2） 隔振效果曲线存在3个谷值频率，第1个谷值频率对应的是上层设备不动时筏架垂向振动的模态，后2个谷值频率分别对应筏架弹性模态和舱段壳体弹性模态；
3） 基座振动响应曲线有4个峰值点，前3个特征峰值频率特征与力传递率曲线一致，分别对应浮筏隔振系统前2阶垂向模态、筏架结构弹性模态，第4个峰值特征对应舱段壳体弹性模态；
4） 随着上层隔振器刚度的降低，动态力传递率降低，隔振效果增加，基座振动加速度级降低，系统振动传递明显减弱。因此，在满足总体要求的前提下，降低上层隔振器刚度可显著提升浮筏隔振系统的声学性能。
3.2 下层隔振器的影响
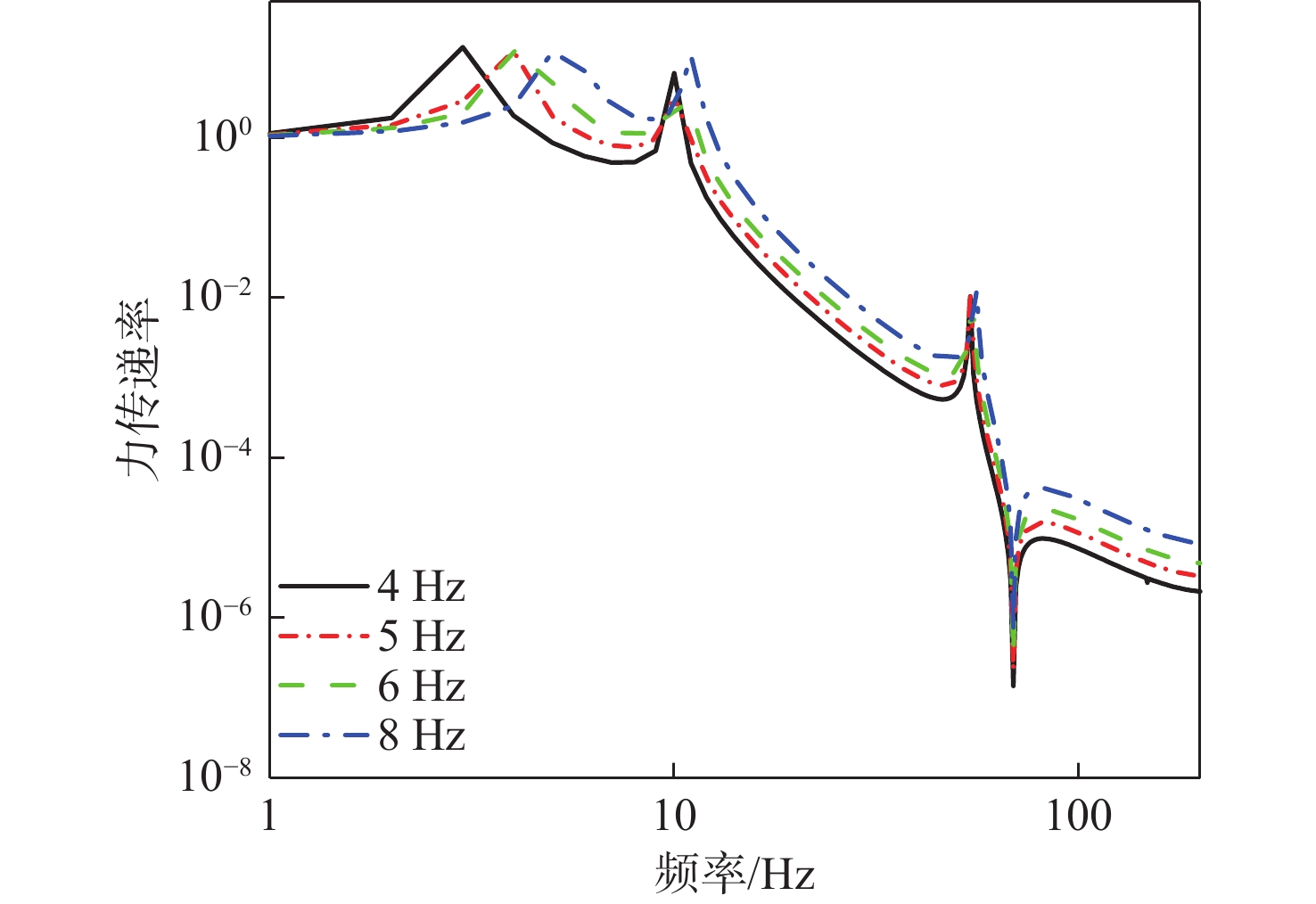
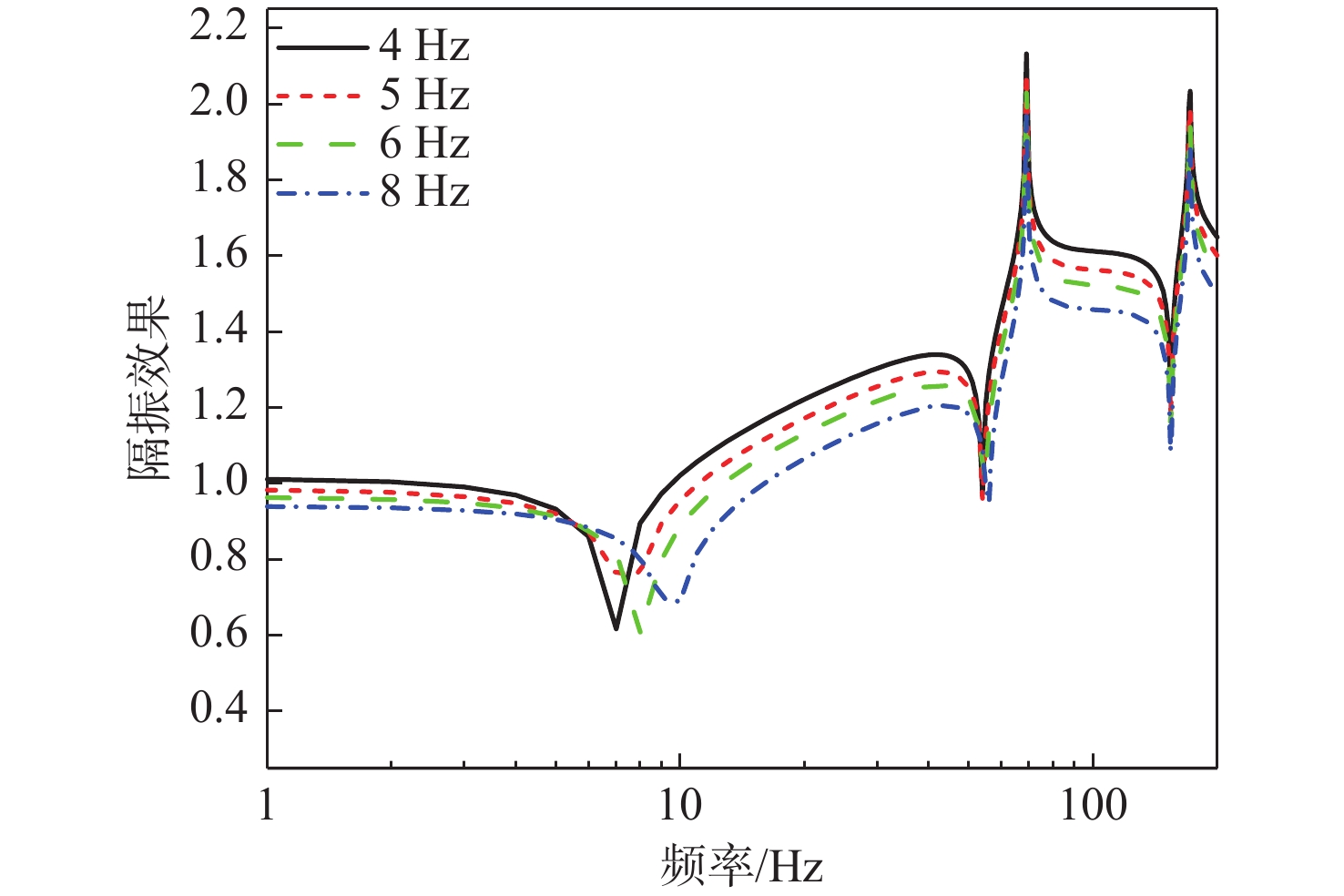
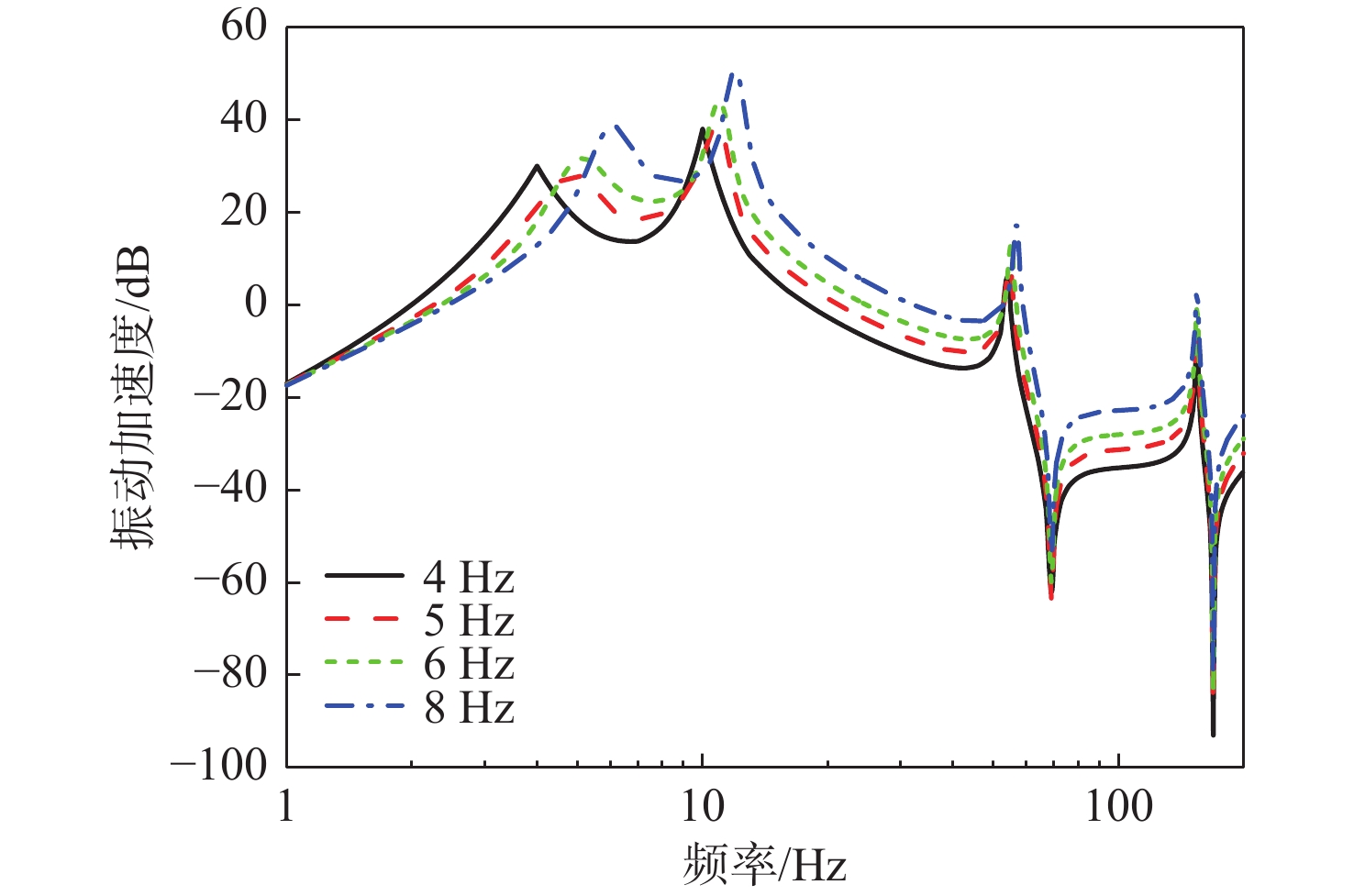
进一步研究下层隔振器刚度对系统振动传递特性影响。保持其他设计要素与基准算例一致，改变下层隔振器刚度k2，使下层隔振器安装频率分别取值4，5，6，8 Hz。计算得到浮筏−舱段耦合系统的动态力传递、隔振效果和舱段基座振动加速度，结果如图13～图15所示。可以看出，随着下层隔振器刚度k2的降低，系统传递特性的一阶共振峰向低频迁移，该频率以上系统动态传递力整体下降，隔振效果增加，基座振动响应降低，系统的声学性能明显提升。因此，在满足总体要求的情况下，降低下层隔振器刚度有利于降低浮筏隔振系统的振动传递。
![]()
图 13 下层隔振器刚度对力传递率的影响Figure 13. Effect of lower isolator stiffness on force transmissibility![]()
图 14 下层隔振器刚度对隔振效果的影响Figure 14. Effect of lower isolator stiffness on vibration isolation effectiveness![]()
图 15 下层隔振器刚度对基座振级的影响Figure 15. Effect of lower isolator stiffness on pedestal vibration level3.3 筏架弹性模态的影响
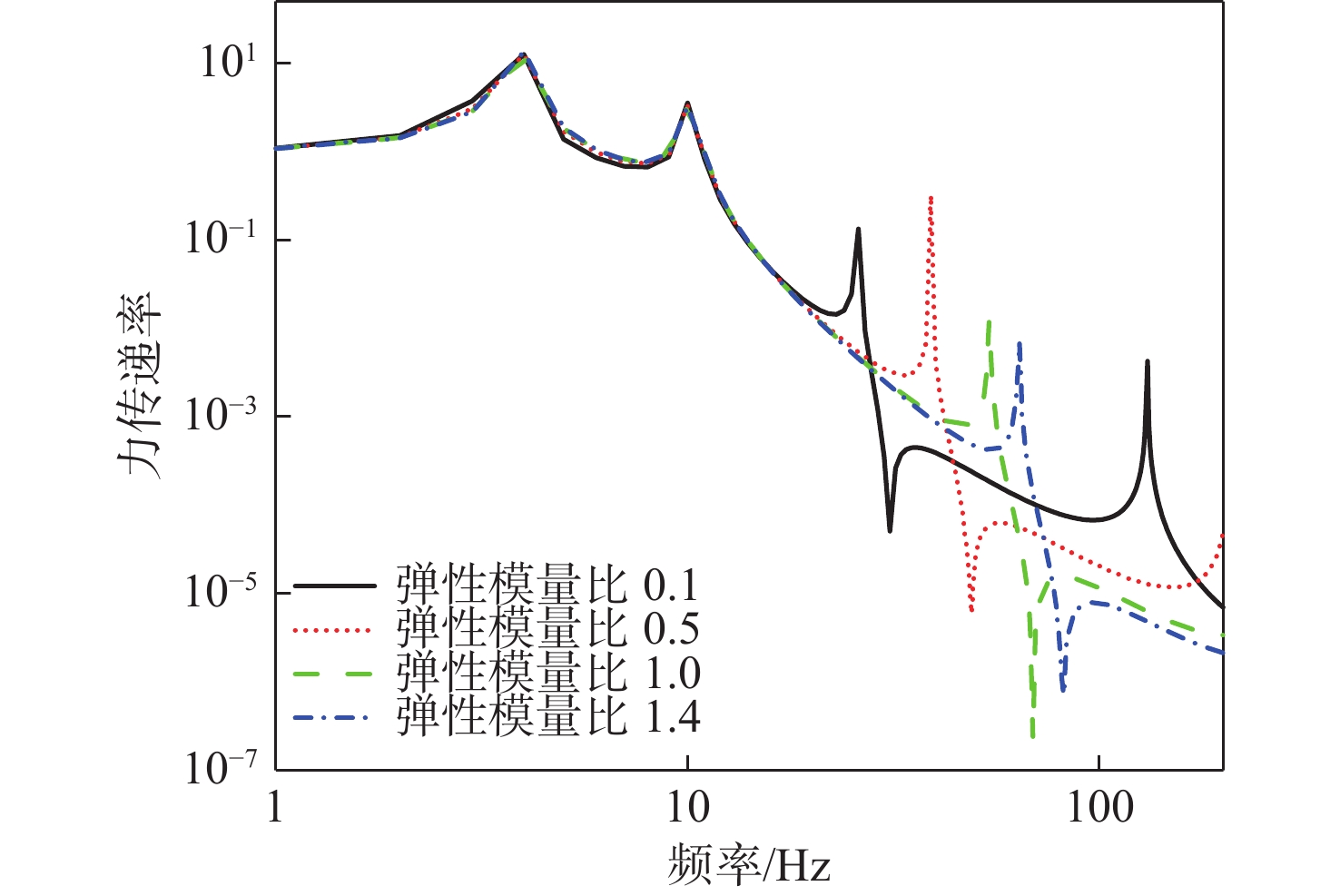
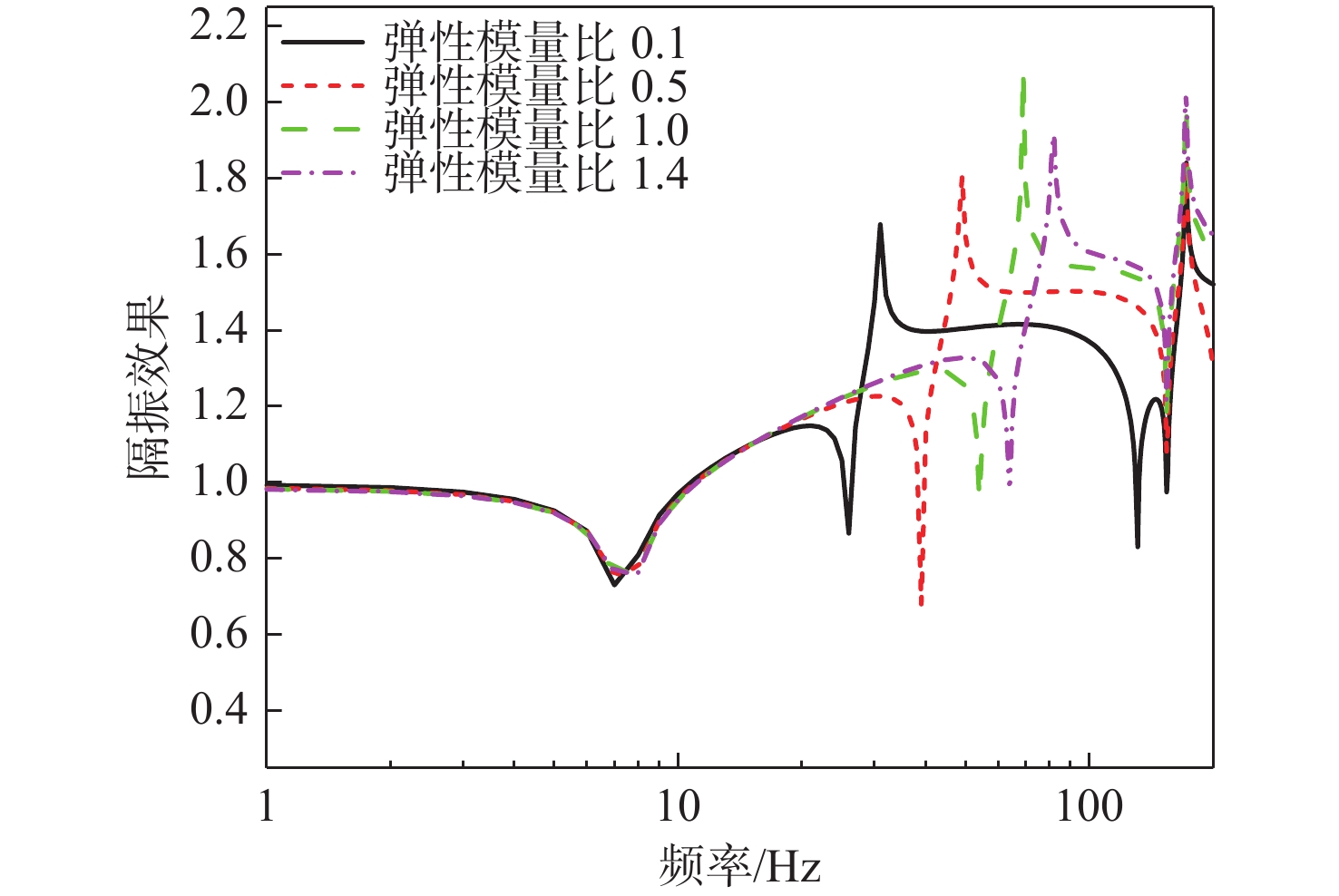
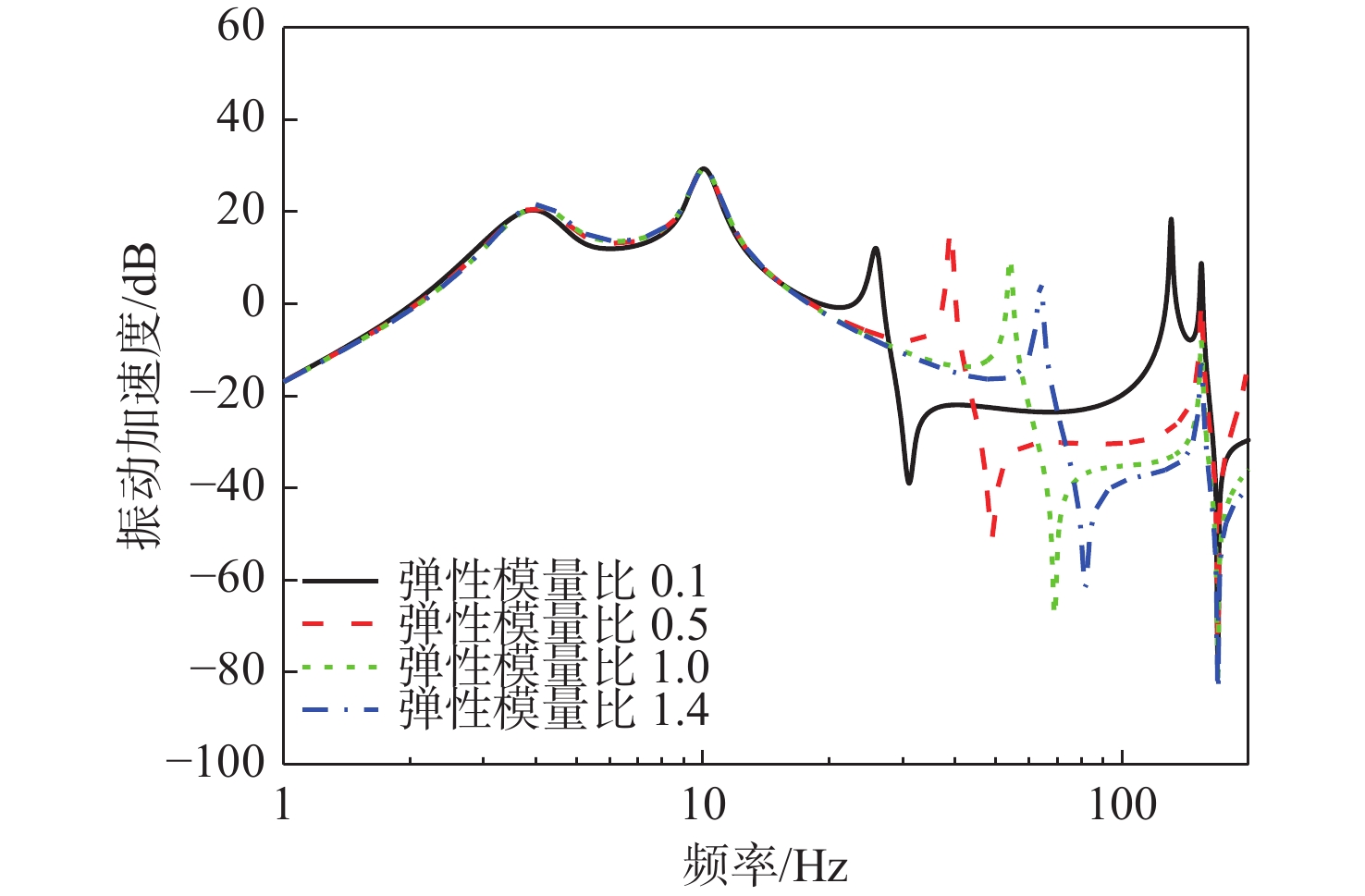
筏架作为舱筏隔振系统的重要组成部分，其振动模态对系统振动传递特性具有重要影响，本节进一步研究筏架弹性模态对系统振动传递特性的影响。保持其他设计要素与基准算例一致，改变筏架结构的弹性弹性模量来控制筏架的刚度，分别取弹性模量为0.1，0.5，1和1.4的基准弹性模量4种工况。计算得到浮筏−舱段耦合系统的动态力传递、隔振效果和基座振级，计算结果如图16～图18 所示。可以看出：
![]()
图 17 弹性模量对隔振效果的影响Figure 17. Effect of elastic modulus on vibration isolation effectiveness1） 随着筏架结构弹性模量的变化，系统低频段的质量、刚度特性基本不变，系统前2阶低频模态峰值频率以及低频力传递率基本一致；
2） 随着筏架结构弹性模量的增加，筏架的刚度增加，其弹性模态频率增大，系统动态力传递低频的响应峰值数量减少，且在筏架结构弹性模态未激发时，系统低频声学性能明显提升；
3） 筏架弹性模态会导致隔振效果出现明显的谷值（即能量泄漏频率），影响隔振性能，随着筏架模态频率的提高，系统低频隔振效果提升。因此，提高筏架结构的刚度、提升筏架模态频率有利于提升隔振系统的低频隔振性能。
3.4 筏架质量的影响
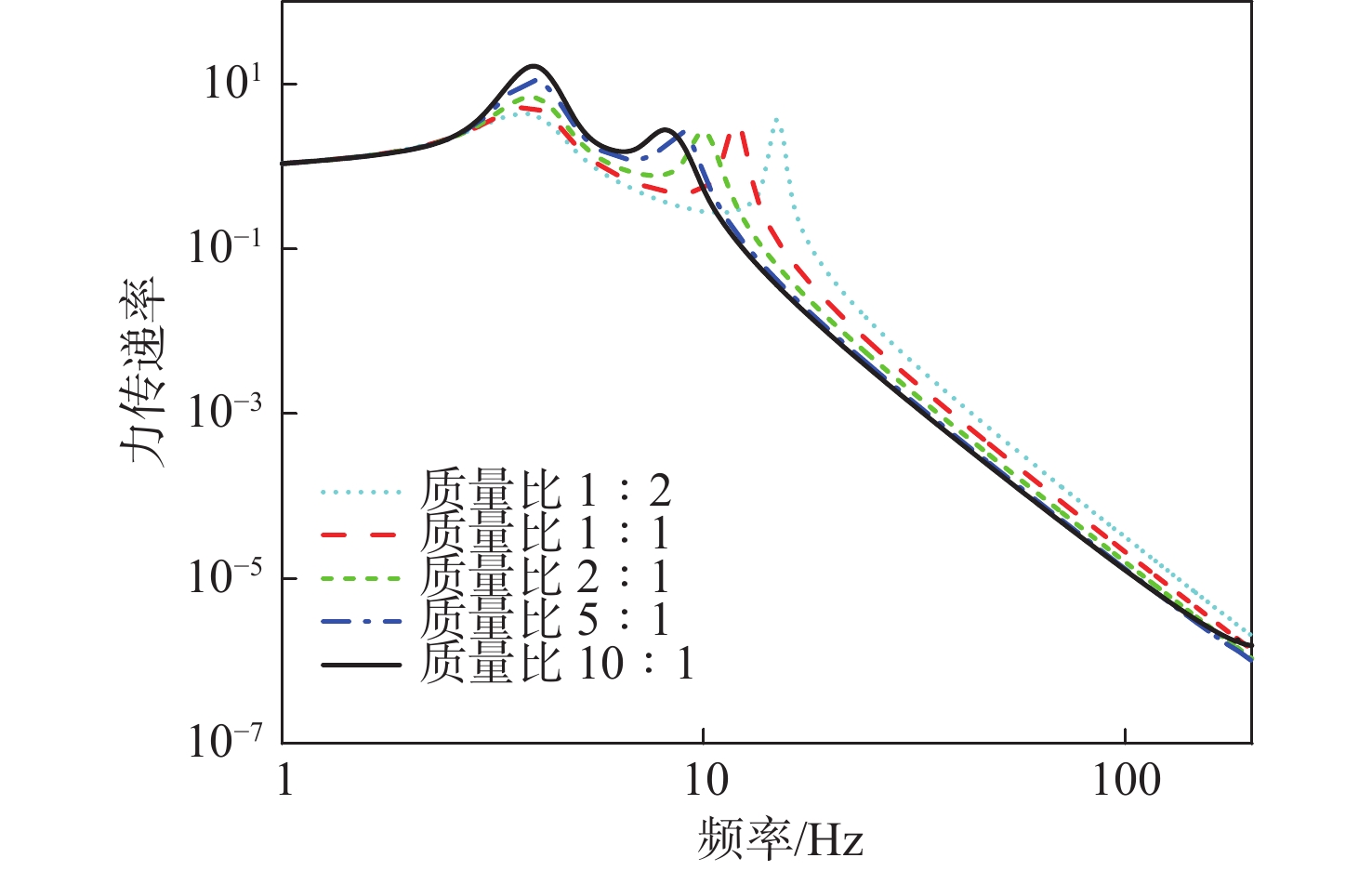
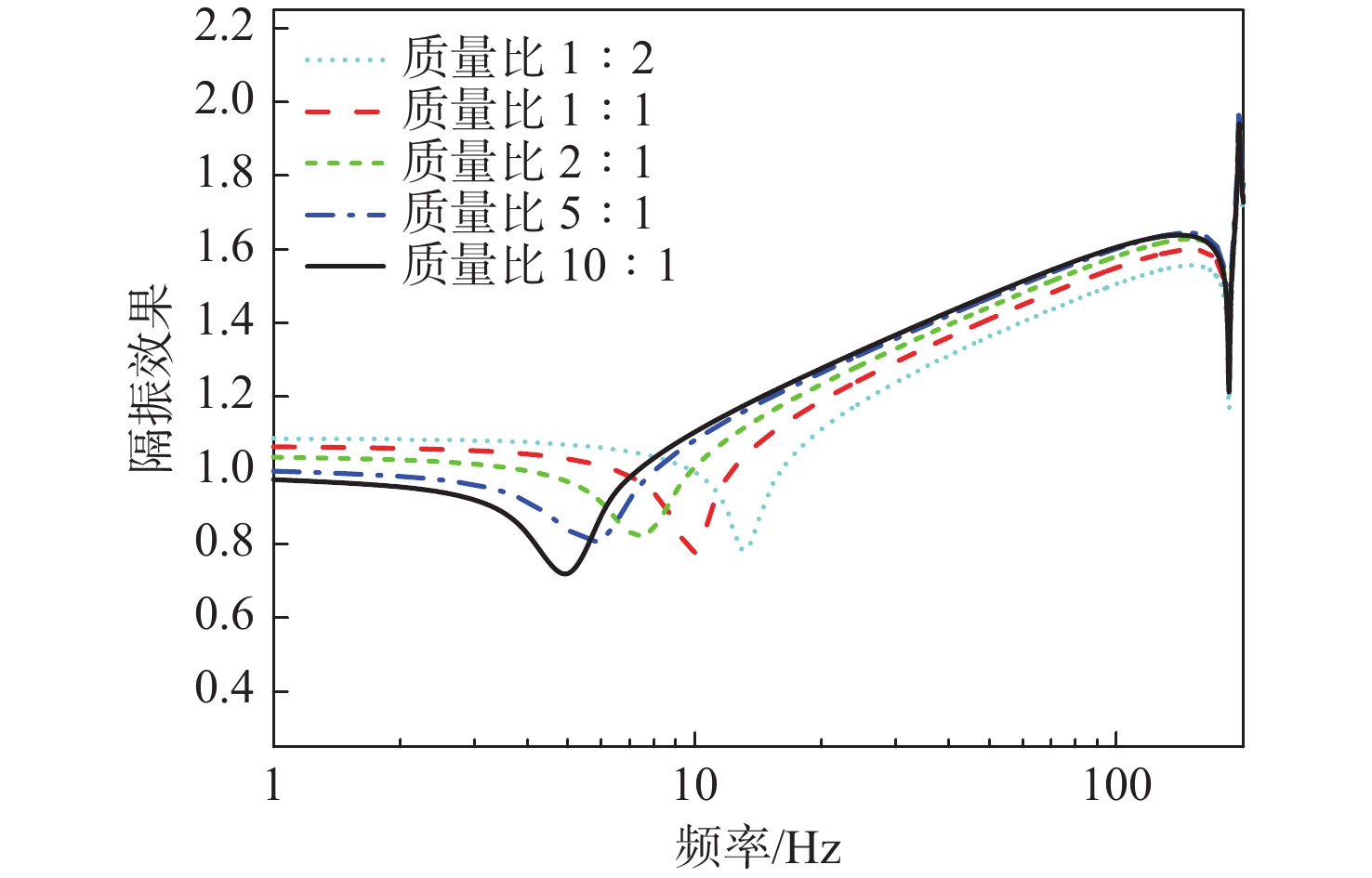
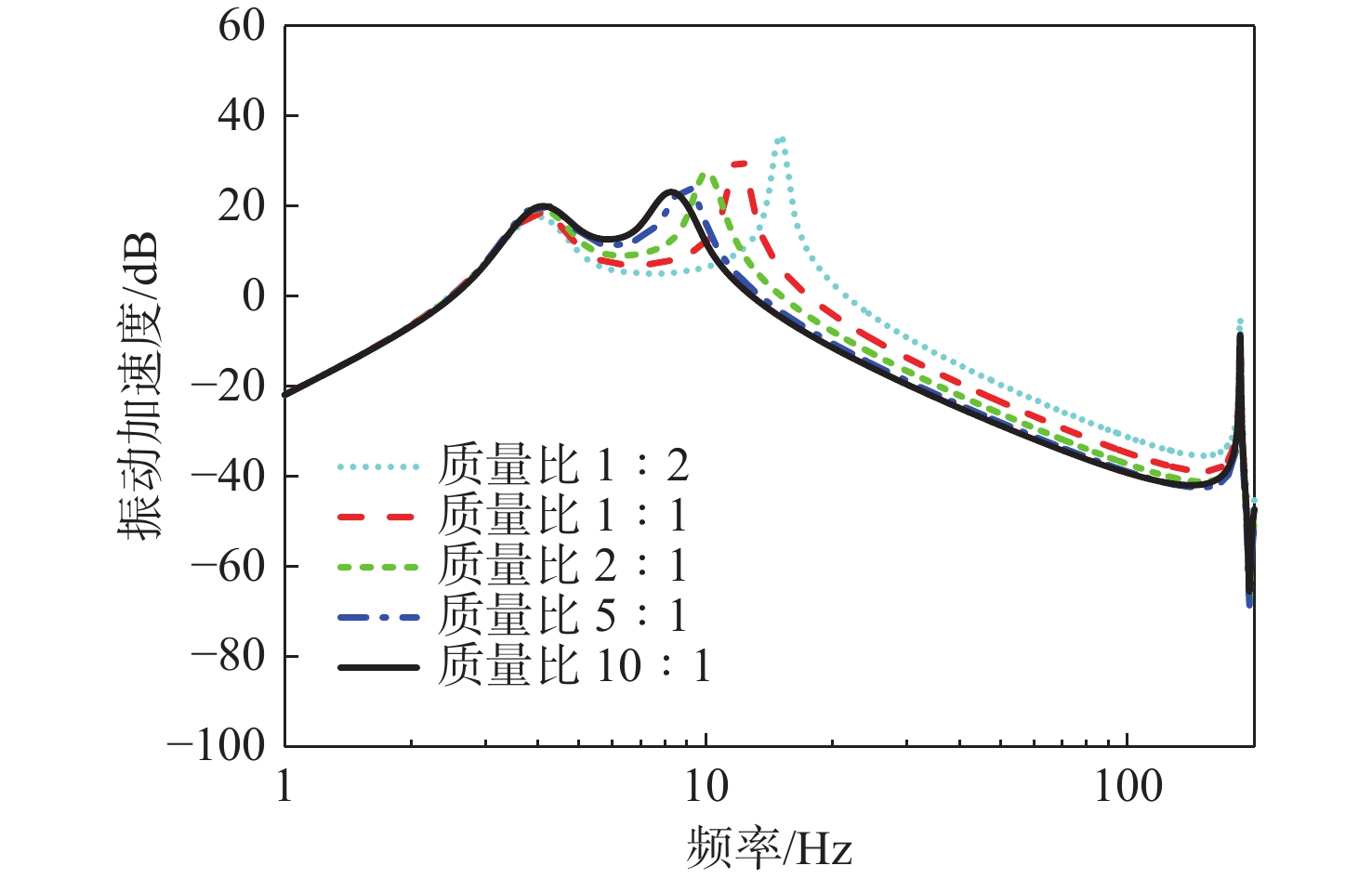
进一步研究筏架−设备质量比对系统振动传递特性的影响。在保持上、下层隔振器安装频率相同的情况下，保持其他设计要素与基准算例一致，通过筏架改变筏架的密度，使筏架质量m2 分别为单个设备质量m1 的0.5，1，2，5倍和10 倍。为避免密度改变影响筏架结构模态频率的耦合影响，将筏架结构杨氏模量调整为5×1014 Pa，并将其设置为刚性体。图19～图21计算结果表明：
1） 随着筏架−设备质量比的增加，系统一阶频率略有升高，二阶频率略有降低。在低频段（10～200 Hz），动态力传递率降低，隔振效果增强，舱段基座振动加速度级降低。因此，增加筏架−设备质量比有利于提升系统的隔振性能。
2） 当筏架−设备质量比m2 / m1=5 时，系统已达到较好的隔振效果。继续增加筏架质量m2仍可进一步提升系统隔振效果，但提升幅度逐渐减小。
3.5 圆柱壳壳体厚度的影响
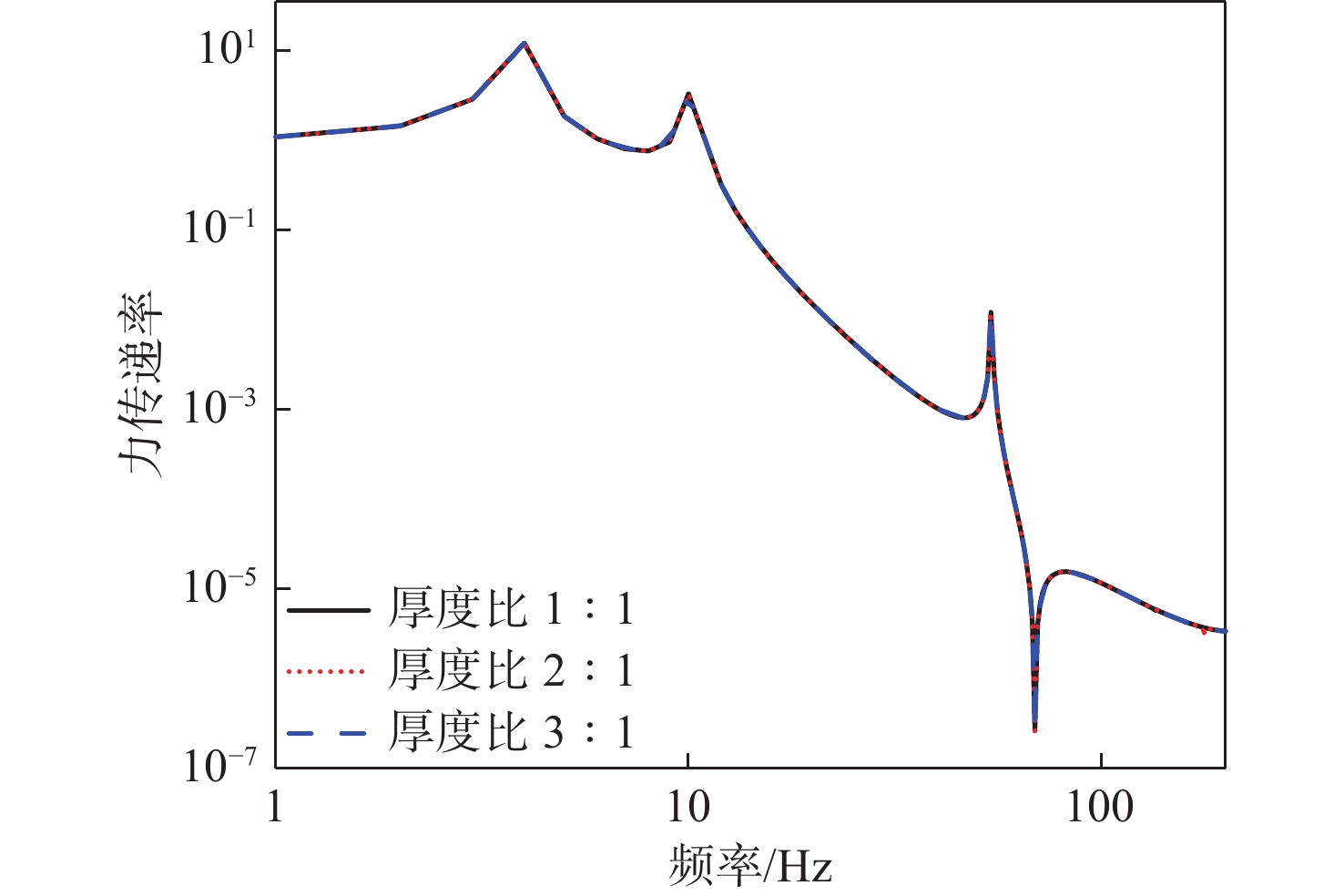
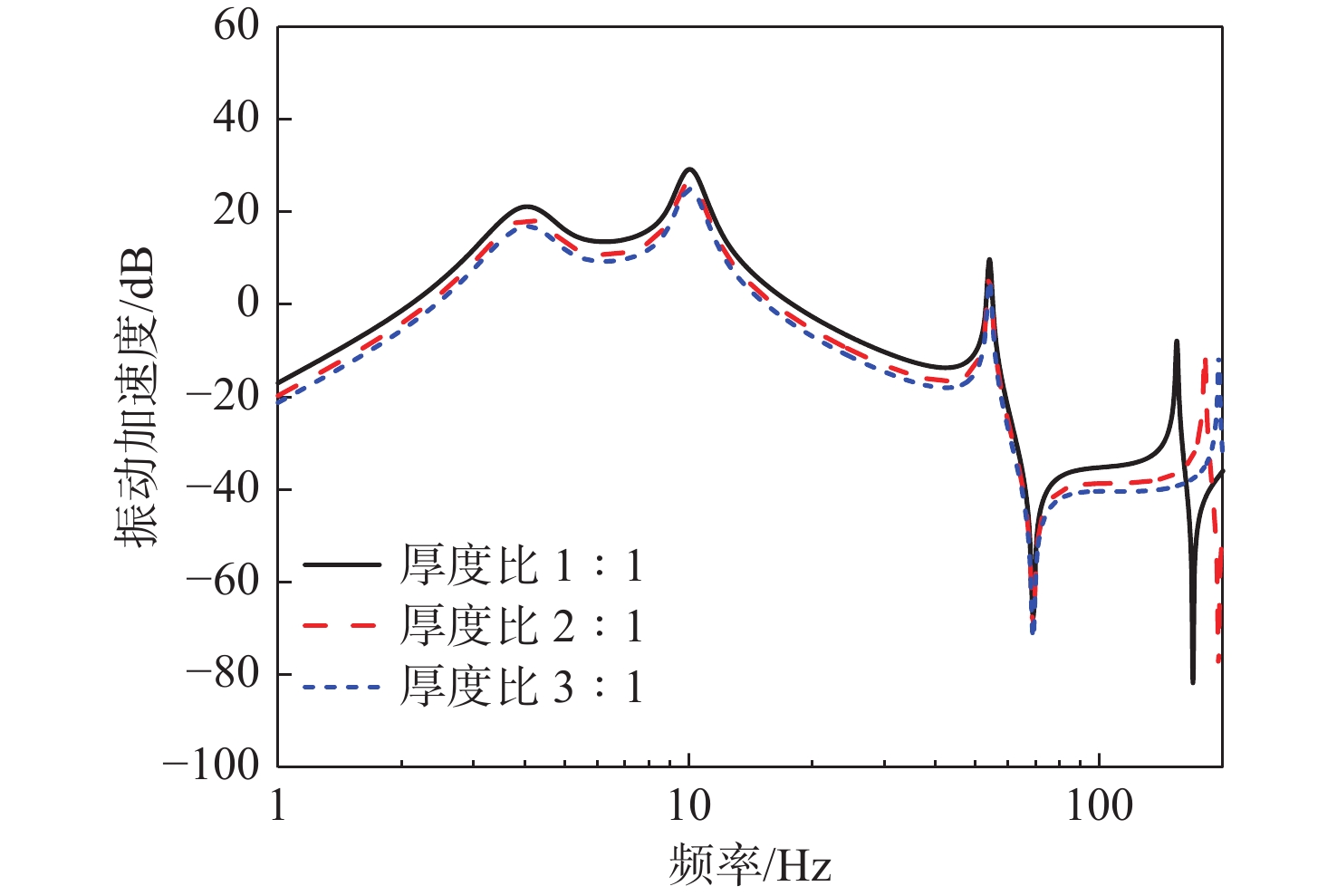
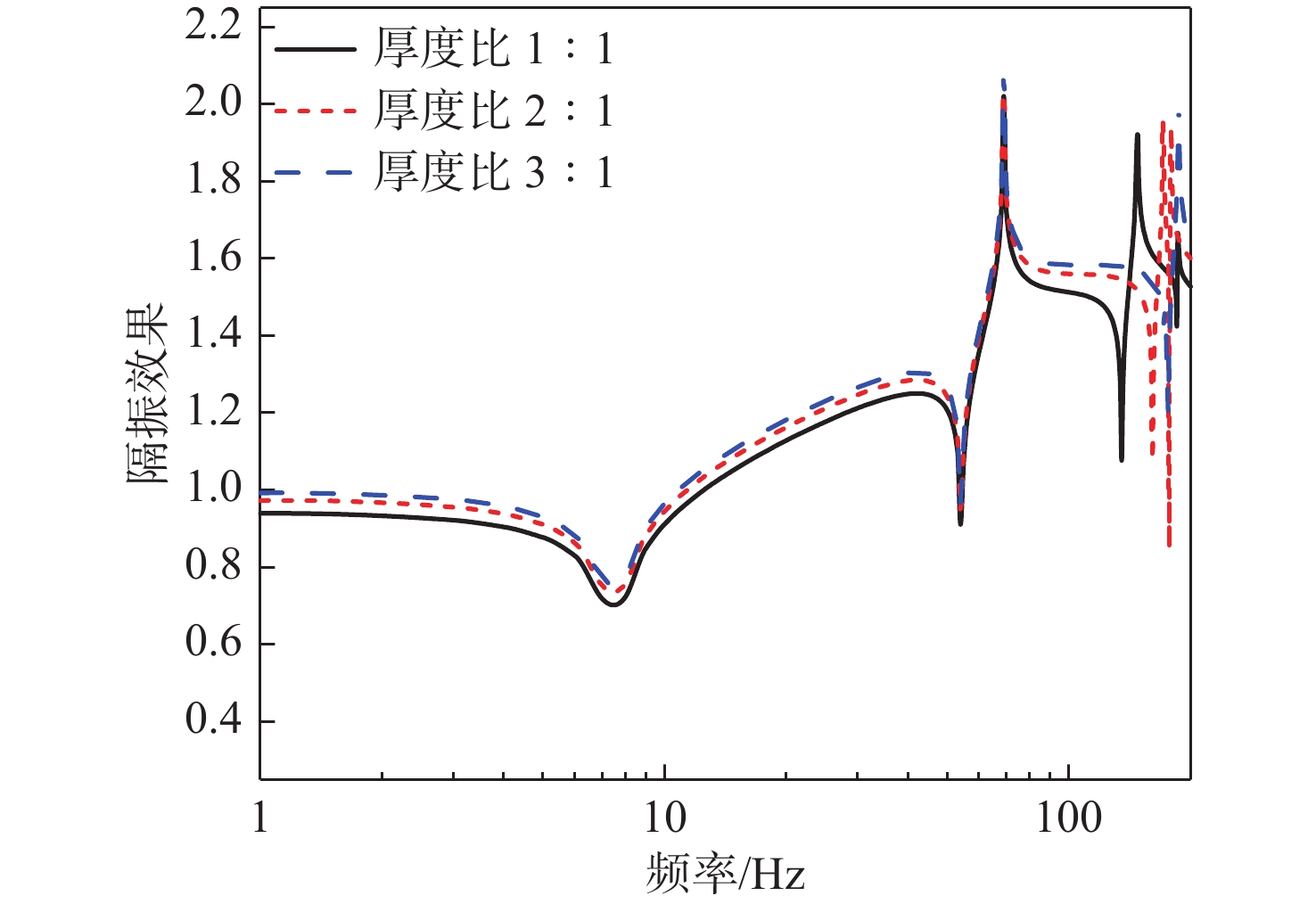
进一步研究舱段圆柱壳体壳板厚度对系统振动传递特性的影响。在基准模型的基础上，分别将圆柱壳体厚度增加到原来的2和3倍，计算基座动态力传递特性、浮筏的振级落差和舱段基座振级，如下图22 ～图24 所示。结果表明：
![]()
图 22 圆柱壳厚度对力传递率的影响Figure 22. Effect of cylindrical shell thickness on force transmissibility.![]()
图 24 圆柱壳厚度对基座振级的影响Figure 24. Effect of cylindrical shell thickness on pedestal vibration level1） 在一定范围内，增大圆柱壳体厚度对系统基座的动态力传递特性影响较小；
2） 在一定范围内，增大圆柱壳体厚度对隔振系统隔振效果有一定的提升，但提升效果有限；
3） 在一定范围内，增大圆柱壳体厚度对舱段基座振级有一定降低作用，但降低效果有限；
4） 由于力传递率主要体现系统的质量刚度特性，当阻抗达到一定范围后，基座阻抗对力传递率的影响较小，因此力传递率曲线基本保持不变。而隔振效果不仅反映系统的质量刚度特性，还与阻抗失配特性相关，增大壳板厚度可提升基座阻抗，从而增强系统隔振效果，降低基座振动加速度级。总体来看，在一定范围内，增大圆柱壳体厚度对系统声学性能有一定提升，但提升效果有限。
![]()
图 23 圆柱壳厚度对隔振效果的影响Figure 23. Effect of cylindrical shell thickness on vibration isolation effectiveness3.6 环形肋骨高度的影响
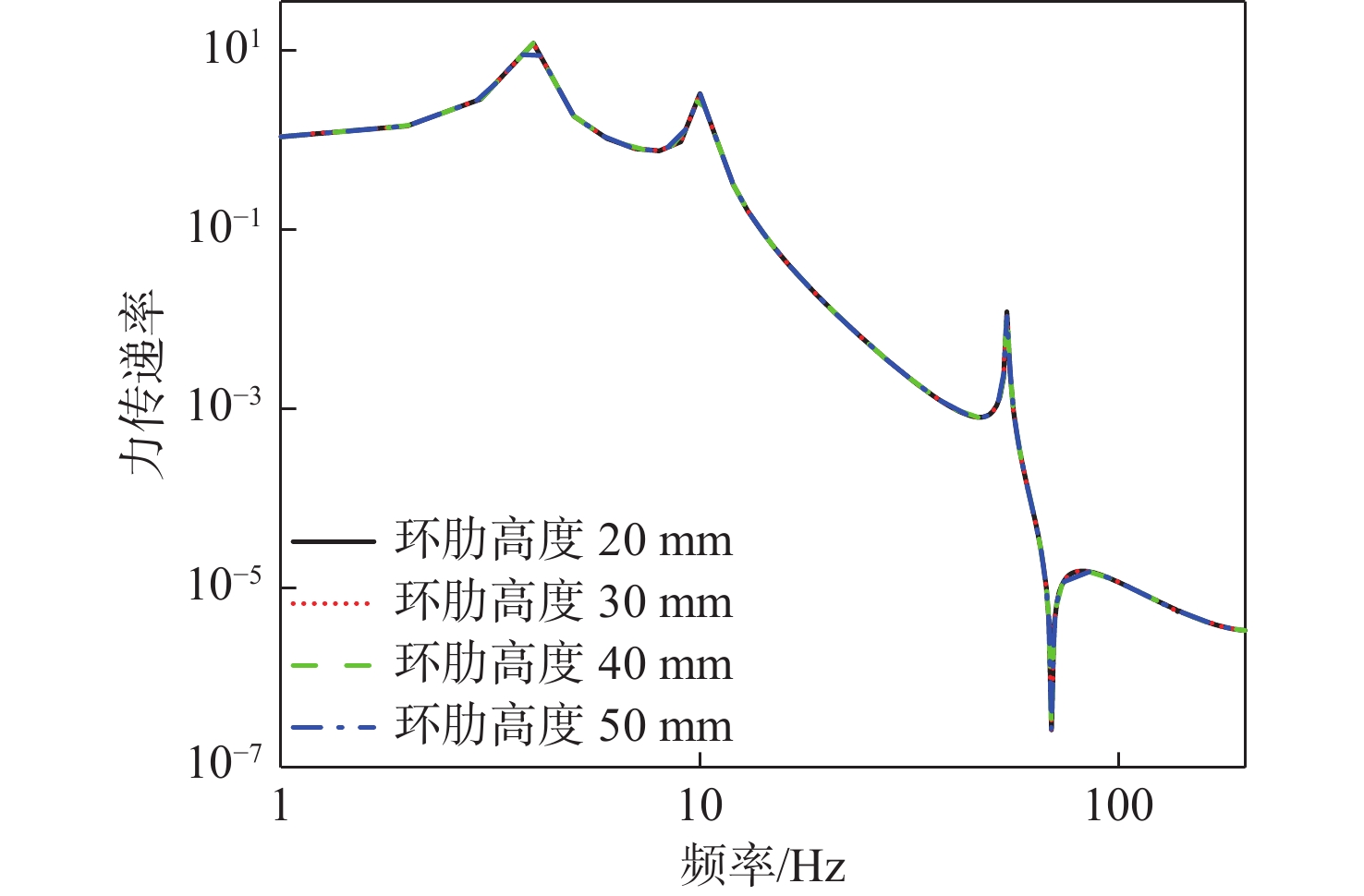
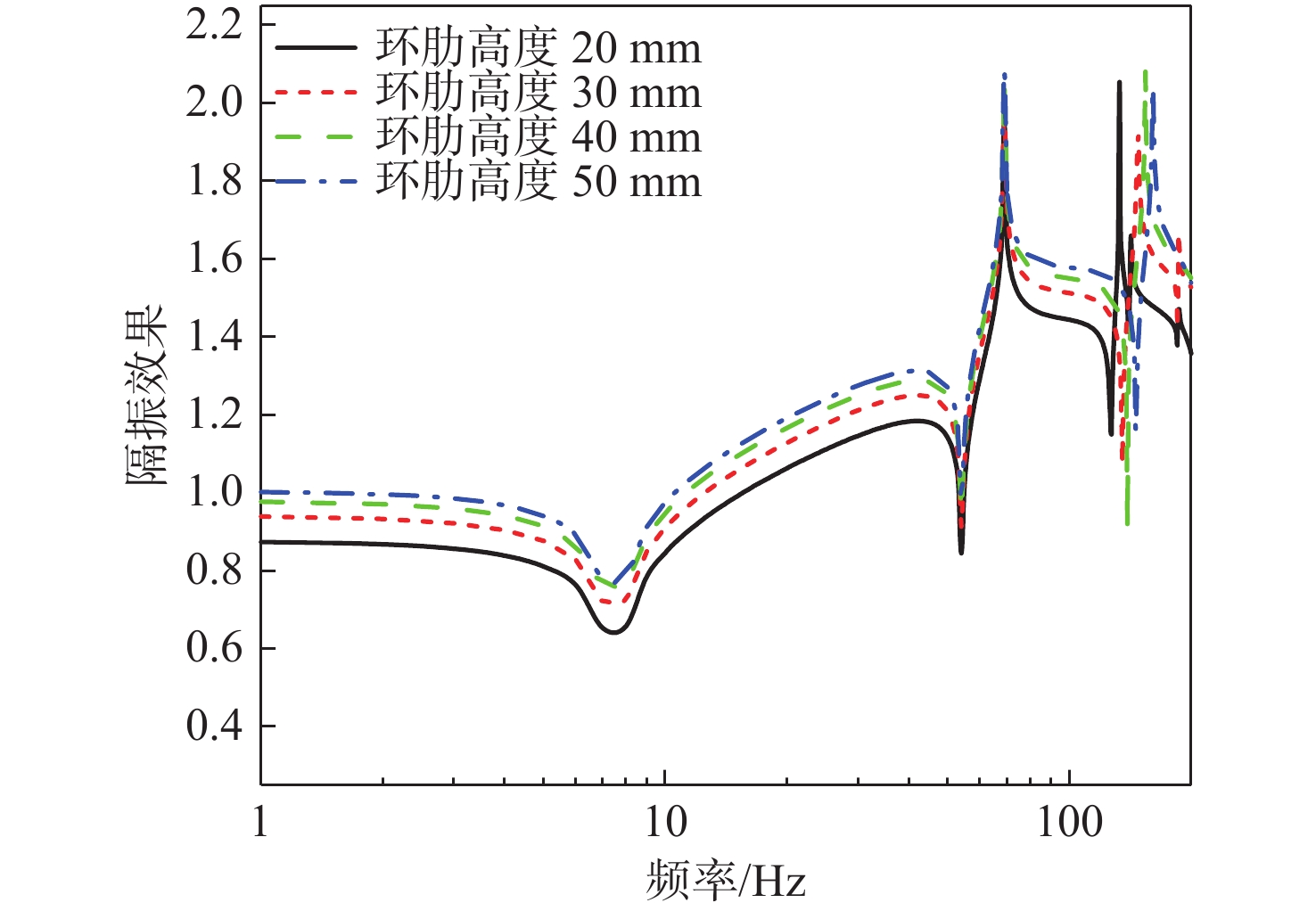
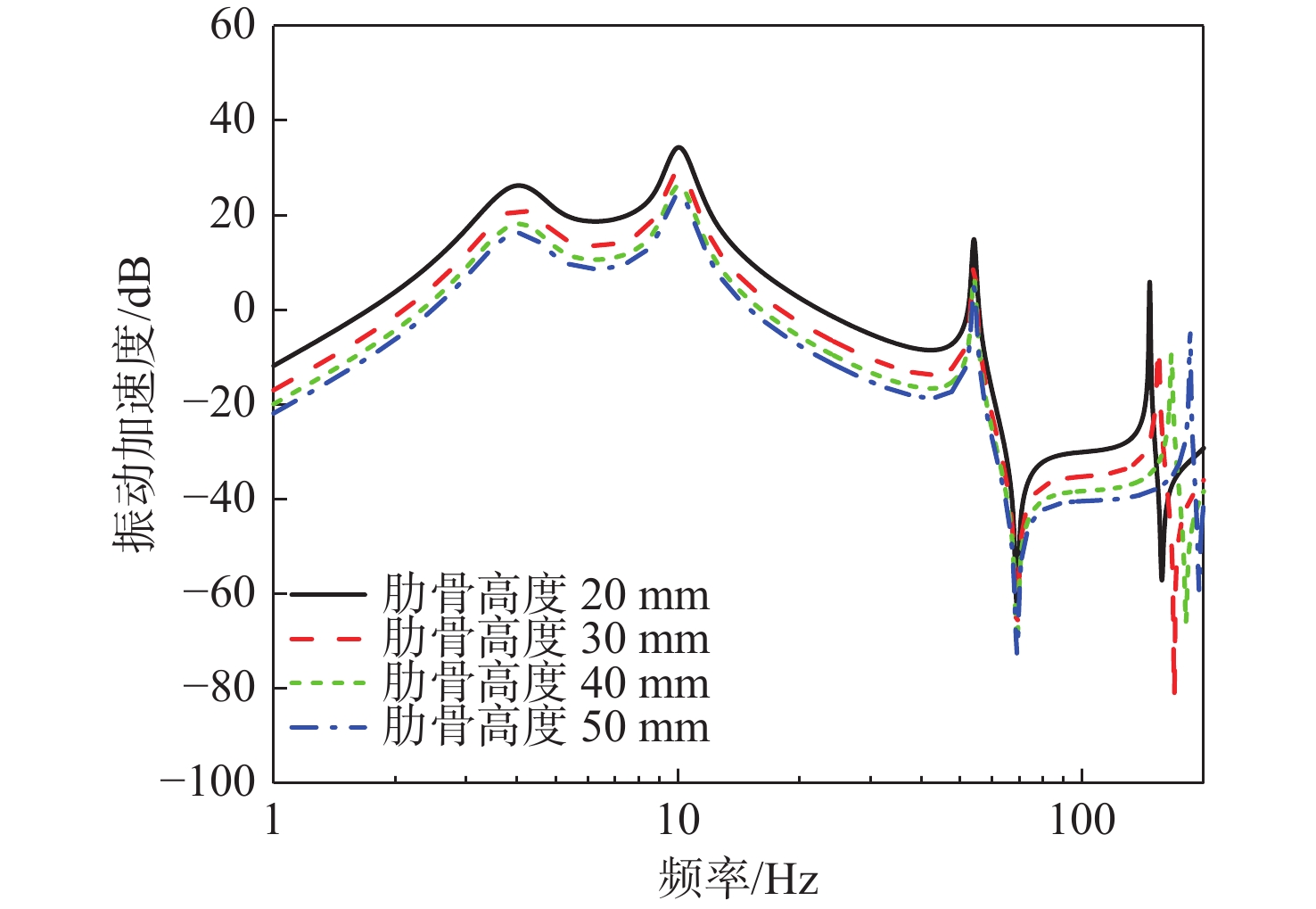
进一步研究舱段圆柱壳体环形肋骨高度对系统振动传递特性的影响。在圆柱壳体环形肋骨高度为30 mm的基准模型的基础上，改变肋骨的高度（20，40，50 mm），计算基座动态力传递特性、浮筏的振级落差及舱段基座振级，如图25～图27所示。计算结果表明：
![]()
图 26 环肋高度对隔振效果的影响Figure 26. Effect of rib height on vibration isolation effectiveness1） 在一定范围内，环形肋骨高度变化对隔振系统基座的动态力传递特性影响不大；
2） 在一定范围内，增大环形肋骨高度，对系统隔振效果有显著的提升，舱段基座振级有明显的降低；
3） 由于力传递率主要体现系统的质量、刚度特性，在基座阻抗达到一定范围后，基座阻抗对力传递率影响不大，力传递曲线基本保持不变；而隔振效果同时反映了系统的质量刚度特性和阻抗失配特性，因此基座阻抗增加，隔振效果有明显提升，舱段基座振级明显降低，系统声学性能提升明显。总体来看，在一定范围内，增大环形肋骨高度，可以显著提高基座阻抗，对系统声学性能提升较为明显。
3.7 环形肋骨宽度的影响
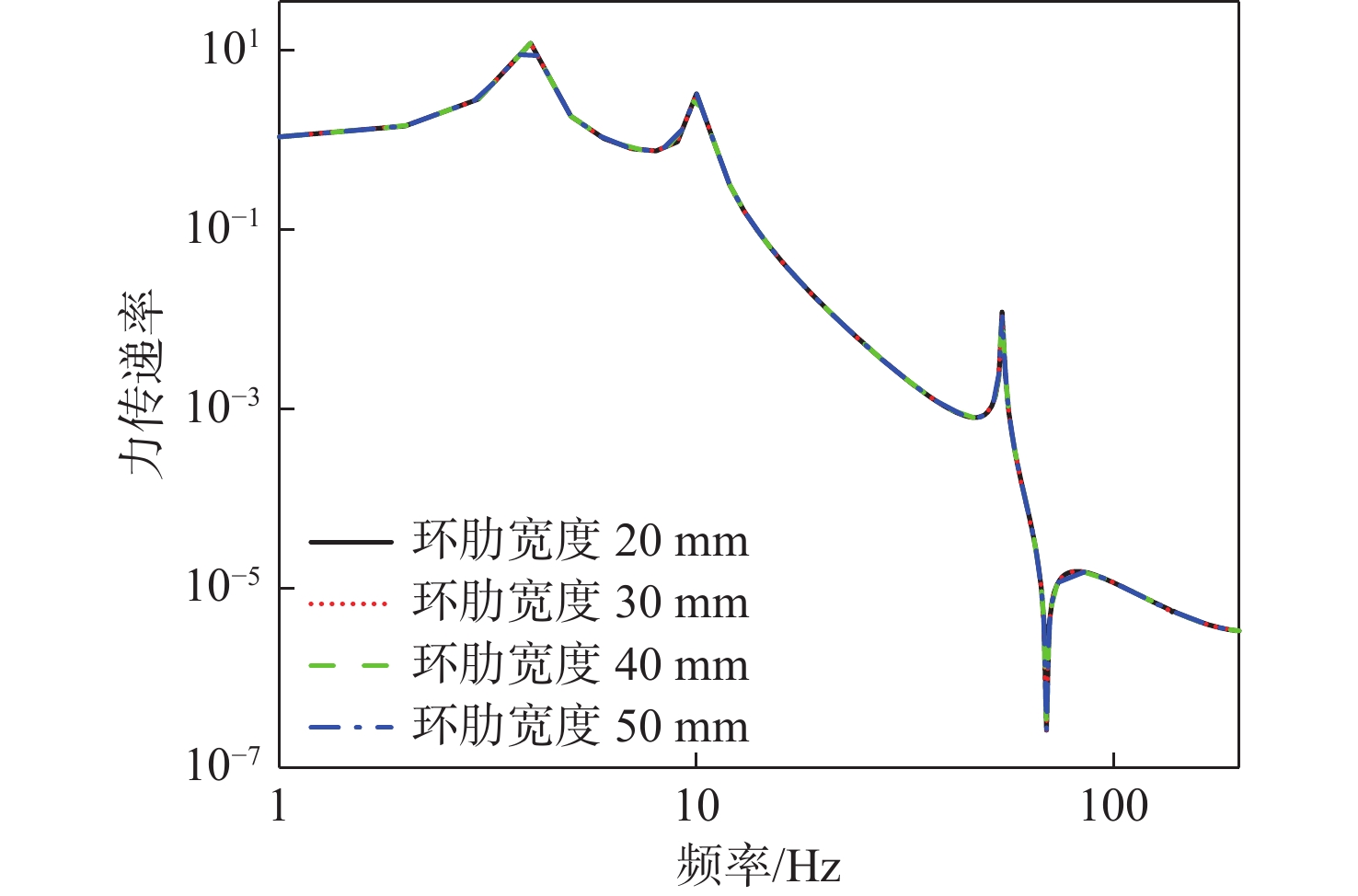
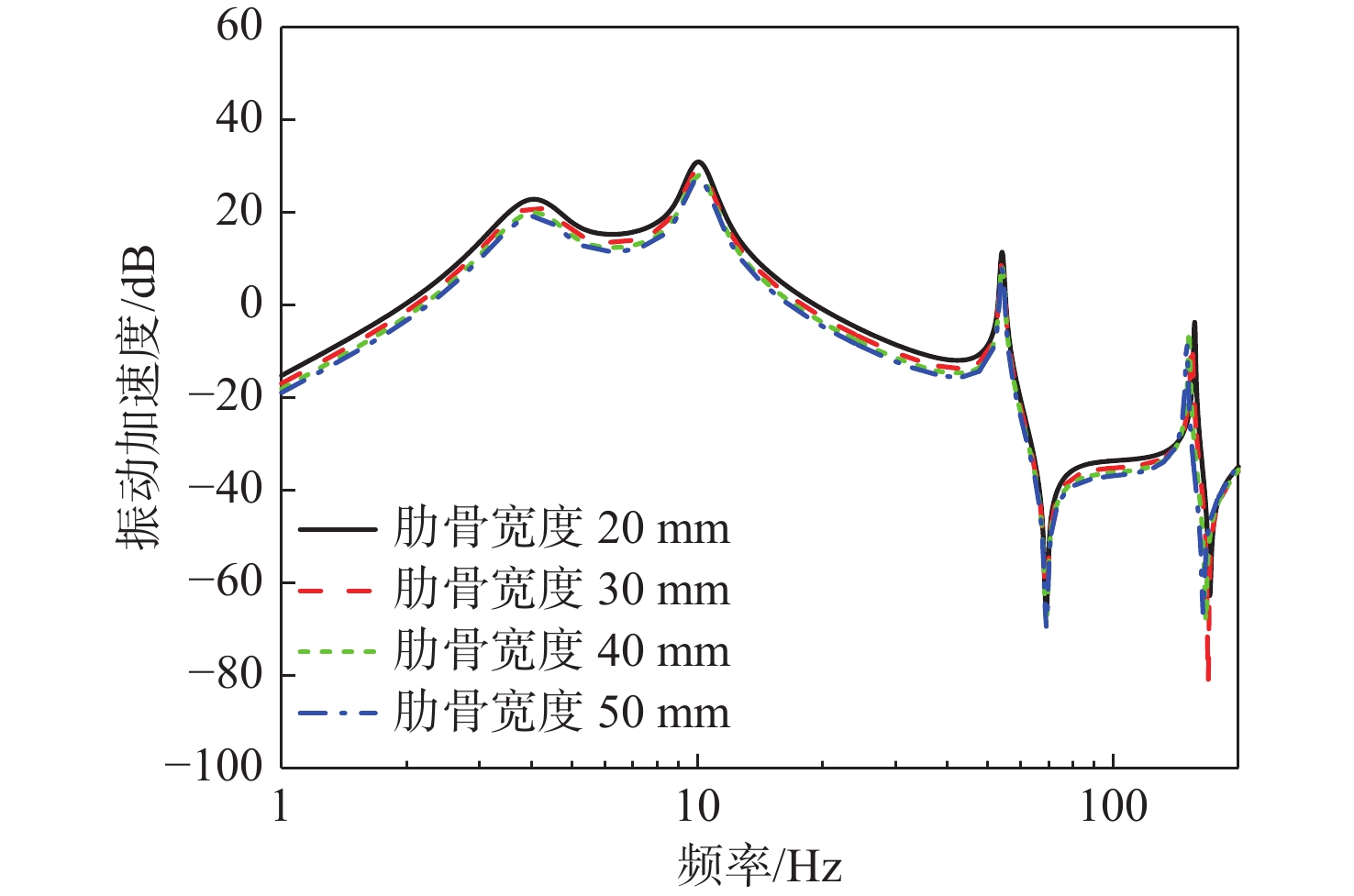
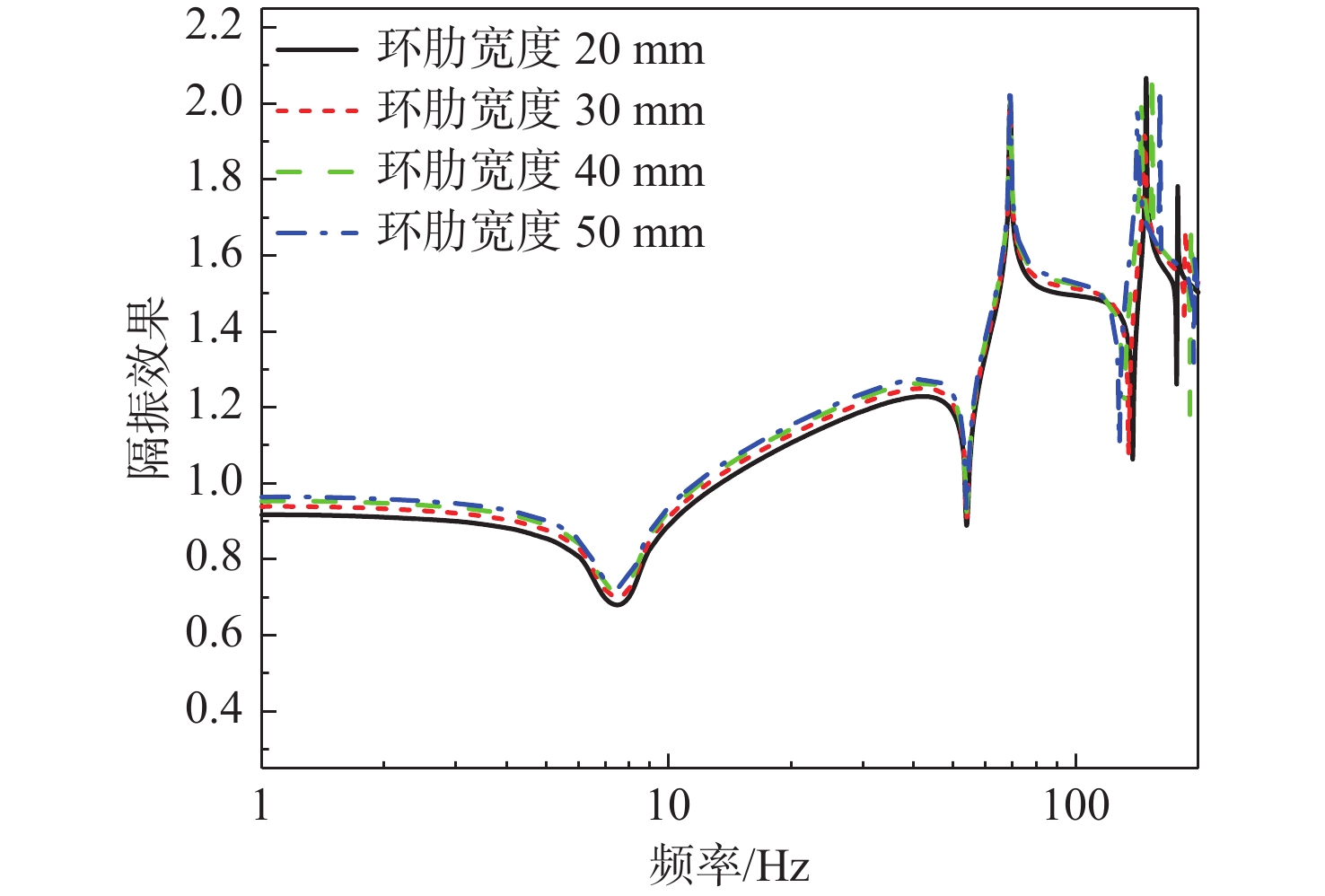
进一步研究舱段圆柱壳体环形肋骨宽度对系统振动传递特性的影响。在圆柱壳体环形肋骨宽度为30mm的基准模型的基础上，分别改变肋骨的宽度分别为20，40，50 mm，计算基座动态力传递特性、隔振效果和舱段基座振级，如图28 ～图30 所示。结果表明：
1） 在一定范围内，环形肋宽度变化对系统基座的动态力传递特性影响不大；
2） 在一定范围内，增大环形肋骨宽度对隔振系统隔振效果有一定的提升，但提升效果有限；
3） 在一定范围内，增大环形肋骨宽度，对于舱段基座振级有一定的降低，但降低效果有限；
4） 由于力传递率主要体现系统的质量、刚度特性，在阻抗达到一定范围后，基座阻抗对力传递率无影响，因此力传递率与基座的性能关系不大，曲线基本保持不变；而隔振效果同时反映了系统的质量、刚度特性和阻抗特性，因此随着基座阻抗的增加，隔振效果有一定提升，基座振级有一定的降低。总体来看，在一定范围内，增大环形肋骨宽度，对于系统声学性能有一定的提升，但提升效果有限。
4. 结 论
本文基于广义变分方法，将浮筏与舱段作为一个整体开展相关动力学分析研究，建立了浮筏−舱段耦合系统动力学分析模型，并基于有限元法验证了广义变分方法建立的浮筏−舱段耦合系统动力学分析模型的正确性。该方法大幅提升了浮筏−舱段耦合系统动力学分析效率并保持了必要的物理直观性，便于研究耦合系统动态特性。基于该模型，系统研究了相关浮筏和舱段结构要素对振动传递特性的影响规律，为浮筏隔振系统优化设计提供了支撑。得到的主要结论如下：
1） 基于广义变分法建立了浮筏−舱段耦合系统动力学模型，经有限元仿真验证，该方法准确性较好，分析效率高，且保持了物理直观性较好；
2） 基于建立的浮筏−舱段耦合系统动力学模型，系统全面研究了浮筏−舱段耦合系统相关设计要素对振动传递特性的影响规律，揭示了浮筏−舱段耦合系统设计要素与其振动传递特性间的影响机制。
3） 对于浮筏−舱段耦合系统优化，上、下层隔振器刚度、筏架结构弹性模态、筏架−设备质量比、舱段环形肋骨高度等因素对系统振动传递特性影响较显著。降低隔振器刚度、提高筏架结构刚度、增大筏架−设备质量比、增大舱段环形肋骨高度可以显著提升系统的声学性能，是浮筏隔振系统优化设计的重点。
-
![]()
图 1 浮筏−舱段耦合系统简化模型示意图
Figure 1. Schematic of the simplified floating-raft-to-compartment coupled system
![]()
图 5 筏架结构上层隔振器安装点振级
Figure 5. Vibration level at upper isolator installation points of raft structure
![]()
图 6 筏架结构下层隔振器安装点振级
Figure 6. Vibration level at lower isolator installation points of raft structure
![]()
图 10 上层隔振器刚度变化对力传递率的影响
Figure 10. Effect of upper isolator stiffness variation on force transmissibility
![]()
图 11 上层隔振器刚度变化对隔振效果的影响
Figure 11. Effect of upper isolator stiffness variation on force transmissibility
![]()
图 12 上层隔振器刚度对基座振级的影响
Figure 12. Effect of upper isolator stiffness on pedestal vibration level
![]()
图 13 下层隔振器刚度对力传递率的影响
Figure 13. Effect of lower isolator stiffness on force transmissibility
![]()
图 14 下层隔振器刚度对隔振效果的影响
Figure 14. Effect of lower isolator stiffness on vibration isolation effectiveness
![]()
图 15 下层隔振器刚度对基座振级的影响
Figure 15. Effect of lower isolator stiffness on pedestal vibration level
![]()
图 17 弹性模量对隔振效果的影响
Figure 17. Effect of elastic modulus on vibration isolation effectiveness
![]()
图 22 圆柱壳厚度对力传递率的影响
Figure 22. Effect of cylindrical shell thickness on force transmissibility.
![]()
图 24 圆柱壳厚度对基座振级的影响
Figure 24. Effect of cylindrical shell thickness on pedestal vibration level
![]()
图 23 圆柱壳厚度对隔振效果的影响
Figure 23. Effect of cylindrical shell thickness on vibration isolation effectiveness
![]()
图 26 环肋高度对隔振效果的影响
Figure 26. Effect of rib height on vibration isolation effectiveness
-
[1] 何琳, 徐伟. 舰船隔振装置技术及其进展[J]. 声学学报, 2013, 38(2): 128–136. doi: 10.15949/j.cnki.0371-0025.2013.02.001 HE L, XU W. Naval vessel machinery mounting technology and its recent advances[J]. Chinese Acta Acustica, 2013, 38(2): 128–136 (in Chinese). doi: 10.15949/j.cnki.0371-0025.2013.02.001
[2] BELTRAN P. Silent vessels technology and the reduction of underwater radiated noise as a significant issue for the future of maritime engineering[C]//International Conference on Marine Design 2020. Cadiz, Spain: Royal Institution of Naval Architects, 2020.
[3] 吴崇健. 浮筏隔振与双层隔振比较研究综述[J]. 舰船工程研究, 1998, 80(1): 29-33. WU C J. Summary of comparative research on floating raft vibration isolation and double-layer vibration isolation[J]. Journal of Ship Engineering research, 1998, 80(1): 29-33 (in Chinese).
[4] 陈森, 万志威, 朱翔, 等. 浮筏隔振系统动力学建模与软件开发[J]. 噪声与振动控制, 2023, 43(4): 14–20. doi: 10.3969/j.issn.1006-1355.2023.04.003 CHEN S, WAN Z W, ZHU X, et al. Dynamic modeling and software development of floating raft vibration isolation systems[J]. Noise and Vibration Control, 2023, 43(4): 14–20 (in Chinese). doi: 10.3969/j.issn.1006-1355.2023.04.003
[5] 黄修长, 徐时吟, 张志谊, 等. 基于频响函数综合的舱筏隔振系统灵敏度分析和优化[J]. 振动与冲击, 2011, 30(5): 145–151. doi: 10.3969/j.issn.1000-3835.2011.05.030 HUANG X C, XU S Y, ZHANG Z Y, et al. Design sensitivity analysis and optimization of a floating raft system using a FRF-based substructuring method[J]. Journal of Vibration and Shock, 2011, 30(5): 145–151 (in Chinese). doi: 10.3969/j.issn.1000-3835.2011.05.030
[6] 吴崇建. 波传播法解析结构振动[M]. 哈尔滨: 哈尔滨工程大学出版社, 2019. WU C J. Wave propagation approach for structural vibration[M]. Harbin: Harbin Engineering University Press, 2019 (in Chinese).
[7] 赵留平. 基于夹层板的浮筏隔振系统有限元分析[J]. 中国舰船研究, 2010, 5(3): 43–46. doi: 10.3969/j.issn.1673-3185.2010.03.010 ZHAO L P. Finite element analysis of floating raft isolation system based on sandwich plate[J]. Chinese Journal of Ship Research, 2010, 5(3): 43–46 (in Chinese). doi: 10.3969/j.issn.1673-3185.2010.03.010
[8] 王永远, 向阳, 周勇, 等. 基于MSC. Patran的浮筏隔振系统性能分析[J]. 船海工程, 2008, 37(3): 9–13. doi: 10.3963/j.issn.1671-7953.2008.03.004 WANG Y Y, XIANG Y, ZHOU Y, et al. Performance analysis of the floating raft system base on the MSC. Patran[J]. Ship & Ocean Engineering, 2008, 37(3): 9–13 (in Chinese). doi: 10.3963/j.issn.1671-7953.2008.03.004
[9] QU Y G, LIANG D, MENG G. Vibration and acoustic waves of multilayered cylindrical shells carrying internal components attached by nonlinear compliant mounts[J]. European Journal of Mechanics-A/Solids, 2020, 83: 104032. doi: 10.1016/j.euromechsol.2020.104032
[10] HE D Z, WANG Q S, ZHONG R, et al. Vibration analysis of functionally graded material (FGM) double layered floating raft structure by the spectro-geometric method[J]. Structures, 2023, 48: 533–550. doi: 10.1016/j.istruc.2022.11.111
[11] QU Y G, HUA H X, MENG G. Vibro-acoustic analysis of coupled spherical-cylindrical-spherical shells stiffened by ring and stringer reinforcements[J]. Journal of Sound and Vibration, 2015, 355: 345–359. doi: 10.1016/j.jsv.2015.06.034
[12] QU Y G, LONG X H, WU S H, et al. A unified formulation for vibration analysis of composite laminated shells of revolution including shear deformation and rotary inertia[J]. Composite Structures, 2013, 98: 169–191. doi: 10.1016/j.compstruct.2012.11.001
[13] 瞿叶高. 基于区域分解−谱边界元法的复合材料结构振动与声辐射问题研究[D]. 上海: 上海交通大学, 2014. QU Y G. Investigation on vibration and sound radiation problems of composite structures based on domain decomposition and spectral boundary element methods[D]. Shanghai: Shanghai Jiao Tong University, 2014 (in Chinese).
[14] QATU M S. Vibration of laminated shells and plates[M]. London: Elsevier Science & Technology, 2004.
[15] ALI A, RAJAKUMAR C. The boundary element method: Applications in sound and vibration[M]. London: CRC Press, 2004.
下载:
计量
- 文章访问数: 63
- HTML全文浏览量: 27
- PDF下载量: 4
