Precise path following of underactuated ship based on neurodynamic optimization and model predictive control
-
摘要:目的
旨在解决传统模型预测控制方法采用在线滚动方式进行优化求解，造成欠驱动船舶路径跟踪预测控制器计算量大的问题。
方法将神经动态优化系统引入模型预测控制方法，提出一种具有实时性的欠驱动船舶路径跟踪预测控制器。首先，针对船舶欠驱动特性，采用并改进视线制导策略：针对传统视线制导策略的运动学模型不确定性问题，基于滑模思想，提出鲁棒视线制导方法；更进一步，针对外界干扰影响下船舶易产生侧滑角问题，对侧滑角进行补偿，提出鲁棒自适应视线制导方法，提高系统对模型不确定性与外界干扰的鲁棒性。其次，针对欠驱动船舶输入饱和问题，通过模型预测控制方法将船舶路径跟踪问题转化为含有输入约束限制的二次优化问题。最后，针对模型预测控制方法采用在线滚动优化策略导致计算负担增加问题，基于投影递归神经网络，建立神经动态优化求解器，通过并行求解含有输入约束限制的二次优化问题，提高计算效率。
结果经过直线和曲线路径跟踪仿真，验证了本文所提出的具有实时性的欠驱动船舶路径跟踪预测控制器能够达到任意路径跟踪的目标。对比仿真实验结果也表明所提方法相较于Fmincon优化求解器（MATLAB内置求解器）计算效率提升约90倍，具有显著优势。
结论研究结果对于提升欠驱动船舶路径跟踪预测控制的实时性能具有一定的工程实用参考价值。
Abstract:ObjectiveThe traditional model predictive control method employs a repeated online optimization approach, resulting in a high computational burden for underactuated ship path-following predictive controller. To address this issue, this paper presents an efficient predictive controller for underactuated ship path following based on the neurodynamic optimization system.
MethodFirst, the line-of-sight (LOS) guidance principle is employed to mitigate the underactuated problem herein; for kinematic model uncertainty in traditional LOS guidance law, a robust LOS guidance method based on the sliding mode concept is proposed. Furthermore, the sideslip angle induced by external disturbances negatively affects path following. To compensate for this effect, a robust adaptive LOS guidance method is proposed, enhancing robustness against model uncertainty and external disturbances. Second, in order to address the input saturation problem, the model predictive control is adopted herein to transform ship path following problem into the quadratic optimization problem with input constraints. Finally, the neurodynamic optimization solver is proposed based on the projection recurrent neural network herein to solve the quadratic optimization problem with input constraints, enhancing the computational efficiency.
ResultsIn this study, both simulations for straight line path following and curved line path following are conducted. Overall, the simulation results show that the presented efficient predictive controller can achieve arbitrary path following. Additionally, the comparative simulations are performed, revealing that the presented method exhibits advantage in computational efficiency compared to the Fmincon optimization solver. Specifically, the neurodynamic optimization solver achieves approximately a 90-fold improvement in computational efficiency compared to the Fmincon optimization solver.
ConclusionThe research results have practical value for improving the real-time performance of underactuated ship path following. In the future, the proposed real-time predictive control method will be extended to the application of multi-ship cooperative predictive control.
-
0. 引 言
随着人工智能的迅速发展，无人船在航海领域展现出广泛的应用前景，比如海底测绘、海上搜救以及海洋资源勘探等多个方面[1]。路径跟踪作为无人船自主航行和高效作业的关键技术之一，受到诸多学者的广泛关注。路径跟踪的控制输出包括纵向位移、横向位移和航向角。然而，大多数水面船舶仅配备舵和螺旋桨，这类船舶控制输入的自由度维数小于路径跟踪控制输出的自由度维数。因此，船舶路径跟踪问题可被定义为欠驱动系统控制问题。
船舶的欠驱动特性限制了控制器的设计，学界通常采用视线制导（line of sight, LOS）方法，降低路径跟踪控制输出的自由度维数，以简化控制器设计[2]。视线制导方法的原理是模拟舵手的操船行为，跟踪目标前方的某一点以达到路径跟踪目的[3]。Pettersen等[4]采用视线制导方法，实现了航路点跟踪控制。为补偿未知侧滑角的影响， Caharija等[5-6]提出积分视线制导律，并实现船舶路径跟踪。白一鸣等[7]改进自适应积分视线制导方法，补偿未知时变洋流的扰动。Liu等[8]基于降阶扩张状态观测器的视线制导律，补偿时变侧滑角的影响。 Fossen[9]采用自适应控制的思想，提出自适应视线制导律，补偿由风、浪和流产生的快速变化的时变侧滑角。余亚磊等[10]提出一种速变视线制导律，缩短系统误差收敛时间。基于滑模的思想，Liu等[11-12]提出鲁棒视线制导律，增强对模型运动学不确定性的鲁棒性。Shi等[13]结合自适应控制理论和滑模的原理，提出鲁棒自适应视线制导律（robust adaptive line of sight, RALOS），在增强对模型不确定性的鲁棒性的同时，补偿侧滑角的影响。因此，本文拟采用鲁棒自适应视线制导律作为欠驱动船舶路径跟踪的制导策略。
在航海实践中，船舶运动具有严格的约束限制，例如舵角变化的幅度不能超过规定的范围。模型预测控制（model predictive control, MPC）是处理各种约束控制问题的有效方法，在船舶路径跟踪的研究中已得到广泛应用。综合滑模控制与模型预测控制，冯鑫等[14]实现了全驱动船舶路径跟踪。郭琳钰等[15]采用基于径向基神经网络的模型预测控制器，抑制模型不确定性对模型预测控制器的干扰，减小了系统的超调量和跟踪误差。李诗杰等[16]在模型预测控制中引入无模型自适应控制作为路径跟踪误差补偿器，修正船舶状态与预测状态之间的误差，提高了路径跟随控制的精度。然而，在模型预测控制滚动优化过程中，当前研究普遍依赖于各类数学计算软件中的内置优化求解器，受限于有限的处理器算力，这一求解过程往往耗时较长，计算负担较重。比如，Shi等[13]选用Fmincon优化求解器（MATLAB内置求解器）作为滚动优化求解工具，受处理器算力的约束，导致求解时间较长。近年来，神经动态优化理论得到发展与完善，凭借其大规模并行运算的能力与快速收敛的特性，已成为求解优化问题的一种有力工具。 Tank等[17]引入能量函数，首次构建一种解决线性优化问题的霍普菲尔德神经网络。Kennedy等[18]建立一种基于罚函数法的神经网络，解决非线性优化问题，但能量函数是不精确的罚函数，只有罚函数因子设定为无穷大时，才可获得优化问题的最优解。Xia等[19-20]建立一种投影递归神经网络（projection-recurrent neural network, PNN）以解决滚动优化求解问题，结构简单，可调参数较少。在控制领域，神经动态优化方法也得到了应用。在输入约束下， 季政等[21]基于递归神经网络提出一种连续时间非线性系统最优跟踪控制问题的近似求解方法，应用于单摆与三通阀液压缸，验证了方法的有效性。
综上所述，为实现具有实时性的欠驱动船舶精确路径跟踪预测控制，本文将对制导律和控制器进行设计。
首先，综合自适应控制理论和滑模思想，提出鲁棒自适应视线制导律，以提高系统对模型不确定性与外界干扰的鲁棒性，并补偿侧滑角的影响。其次，针对船舶输入饱和问题，采用模型预测控制将路径跟踪问题转化为含有输入约束限制的二次优化问题。最后，基于投影递归神经网络，建立神经动态优化求解器，并行地求解含有输入约束限制的二次优化问题，以提高计算效率。
综合本文所提出的制导律和控制器，将有望增强对模型不确定性的鲁棒性，补偿侧滑角影响，提升路径跟踪预测控制的实时性能。
1. 预备知识及问题描述
1.1 船舶运动数学模型
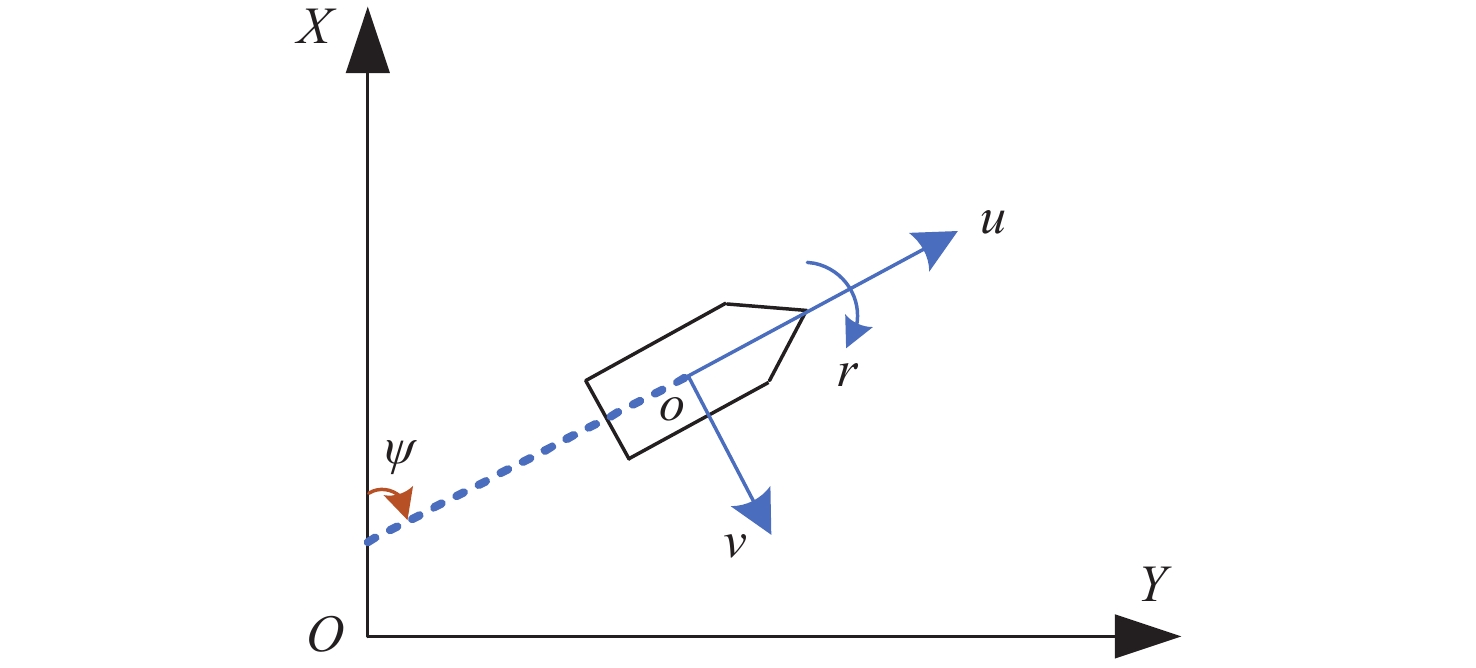
为降低欠驱动船舶路径跟踪问题的复杂度，本文在二维平面内进行研究，即仅考虑纵荡、横荡和艏摇这3个自由度。如图1所示，O-XY为大地坐标系，o-uv为附体坐标系。
船舶运动数学模型表示为：
\begin{split} & \dot {\boldsymbol{\eta}} = {\boldsymbol{R}}\left( \psi \right){\boldsymbol{\chi}} \\& {\boldsymbol{M}}\dot {\boldsymbol{\chi}} ={\boldsymbol{ \tau }}- {\boldsymbol{C}}\left( {\boldsymbol{\chi}} \right){\boldsymbol{\chi}} - {\boldsymbol{D}}\left( {\boldsymbol{\chi}} \right){\boldsymbol{\chi}} \end{split} (1) 式中：{\boldsymbol{\eta}} = {\left[ {x\;}\;\;{y\;}\;\;\psi \right]^{\rm{T}}}，其中x和y为船舶纵向和横向位移，\psi 为航向角；{\boldsymbol{\chi}} = {\left[ {u\;}\;\;{v\;}\;\;r \right]^{\rm{T}}}，其中u和v为纵向速度和横向速度，r为艏摇角速度；{\boldsymbol{\tau}} = {[ {{\tau _{\rm{u}}}\;}\;\;{0\;}\;\;{{\tau _{\rm{r}}}} ]^{\rm{T}}}，其中{\tau _{\rm{u}}}和{\tau _{\rm{r}}}分别为纵向推进力和转艏力矩；{\boldsymbol{R}}(\psi )为转换矩阵，表示为
{\boldsymbol{R}}\left( \psi \right) = \left[ \begin{matrix} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{matrix} \right] M为惯性矩阵，表示为
{\boldsymbol{M}} = \left[ \begin{matrix} {{m_{11}}}&0&0 \\ 0&{{m_{22}}}&{{m_{23}}} \\ 0&{{m_{32}}}&{{m_{33}}} \end{matrix} \right] 式中：{m_{11}} = m - {X_{\dot {u}}}，其中m为船舶质量；{m_{22}} = m - {Y_{\dot {{v}}}}；{m_{33}} = {I_{{z}}} - {N_{\dot {{r}}}}，其中{I_{{z}}}为转动惯量；{m_{23}} = m{x_{{g}}} - {Y_{\dot {{r}}}}，其中{x_{{g}}}为船舶重心纵向坐标；{m_{32}} = m{x_{{g}}} - {N_{\dot {{v}}}}。
{\boldsymbol{C}}({\boldsymbol{\chi }})和{\boldsymbol{D}}({\boldsymbol{\chi}} )分别为科里奥利向心矩阵和阻尼矩阵，分别表示为
{\boldsymbol{C}}\left({\boldsymbol{\chi}} \right)=\left[\begin{matrix} 0& 0& c_{13}({\boldsymbol{\chi}} )\\ 0& 0& c_{23}({\boldsymbol{\chi}} )\\ -c_{13}({\boldsymbol{\chi}} )& -c_{23}({\boldsymbol{\chi}} )& 0 \end{matrix}\right] {\boldsymbol{D}}({\boldsymbol{\chi}} )=\left[\begin{matrix} d_{11}({\boldsymbol{\chi}} )& 0& 0\\ 0& d_{22}({\boldsymbol{\chi}} )& d_{23}({\boldsymbol{\chi}} )\\ 0& d_{32}({\boldsymbol{\chi}} )& d_{33}({\boldsymbol{\chi}} ) \end{matrix}\right] 其中：
\begin{gathered} c_{13}(\boldsymbol{\chi})=-m_{22}v-m_{23}r\\ c_{23}(\boldsymbol{\chi})=m_{11}u \\ d_{11}(\boldsymbol{\chi})=-X_{{u}}-X_{\left|{u}\right|{u}}\left|u\right|-X_{{uuu}}u^2\\ d_{22}(\boldsymbol{\chi})=-Y_{{v}}-Y_{\left|{v}\right|{v}}\left|v\right|- Y_{\left|{r}\right|{v}}\left|r\right|\\ d_{23}(\boldsymbol{\chi})=-Y_{{r}}-Y_{\left|{v}\right|{r}}\left|v\right|-Y_{\left|{r}\right|{r}}\left|r\right|\\ d_{32}(\boldsymbol{\chi})=-N_{{v}}- N_{\left|{v}\right|{v}}\left|v\right|-N_{\left|{r}\right|{v}}\left|r\right|\\ d_{33}(\boldsymbol{\chi})=-N_{{r}}-N_{\left|{v}\right|{r}}\left|v\right|-N_{\left|{r}\right|{r}}\left|r\right| \end{gathered} 以上构成船舶运动数学模型，其中 {X}_{(·)} ， {Y}_{(·)} ， {N}_{(·)} 为水动力导数，但个别参数无法准确获取[22]，因此船舶运动数学模型具有不确定性。
1.2 投影递归神经网络
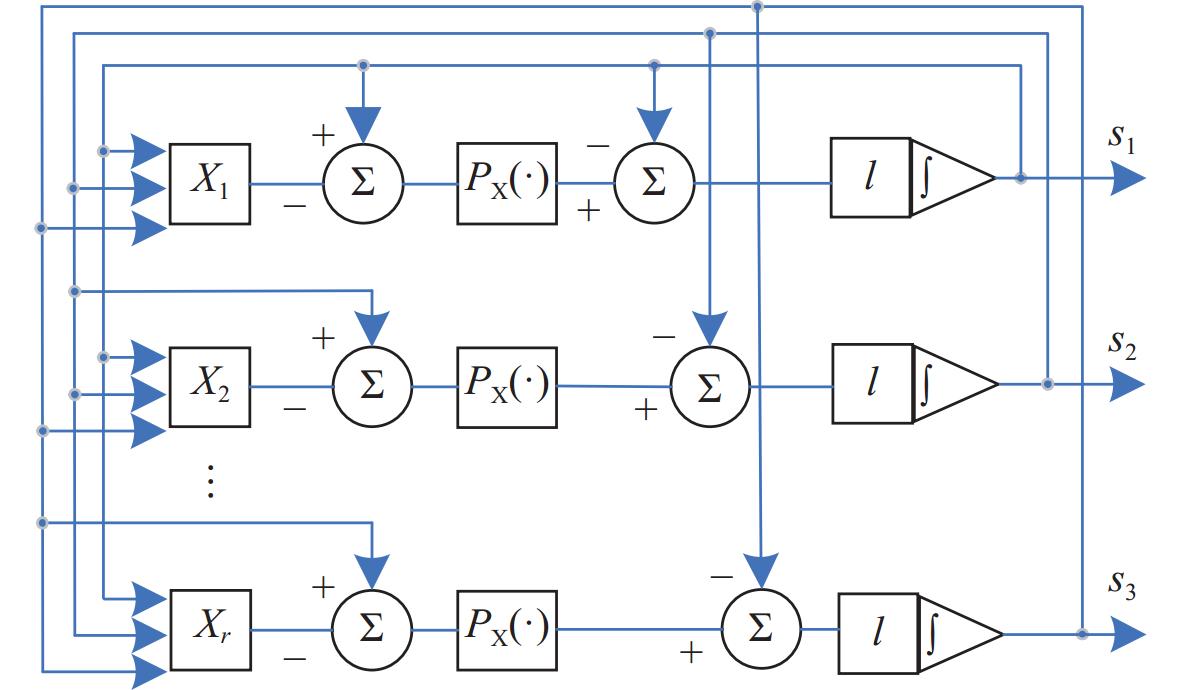
在实际应用中，采用模型预测控制方法时，由于滚动优化过程计算量较大，导致求解时间较长，因此难以实现实时控制。为提升模型预测控制的计算效率，本部分将介绍一种神经动态优化求解器。图2为投影递归神经网络示意图。
在投影递归神经网络的基础上，建立神经动态优化求解器为
\dot {\boldsymbol{s}} = - \iota \left( {{\boldsymbol{s}} - {{\boldsymbol{P}}_{\rm{X}}}({\boldsymbol{s}} - {\boldsymbol{X}}({\boldsymbol{s}}))} \right) (2) 式中： \boldsymbol{s}=\left[s_1\; \; \; s_2\; \; \; \cdots\; \; \; s_{\rm{\mathit{r}}}\right]^{\rm{T}} ；{\boldsymbol{X}}({\boldsymbol{s}}) = \nabla {\boldsymbol{f}}({\boldsymbol{s}})；\iota 为神经网络设计参数。
投影算子为
{P_{\rm{X}}}({s_i}) = \left\{ \begin{aligned} & {d_{\max }},&& {s_i} \geqslant {d_{\max }} \\& {s_i},&& {d_{\min }} < {s_i} < {d_{\max }} \\ & {d_{\min }},&& {s_i} \leqslant {d_{\min }} \end{aligned}\right.,\;\;i = 1,2 \cdots r (3) 1.3 问题描述
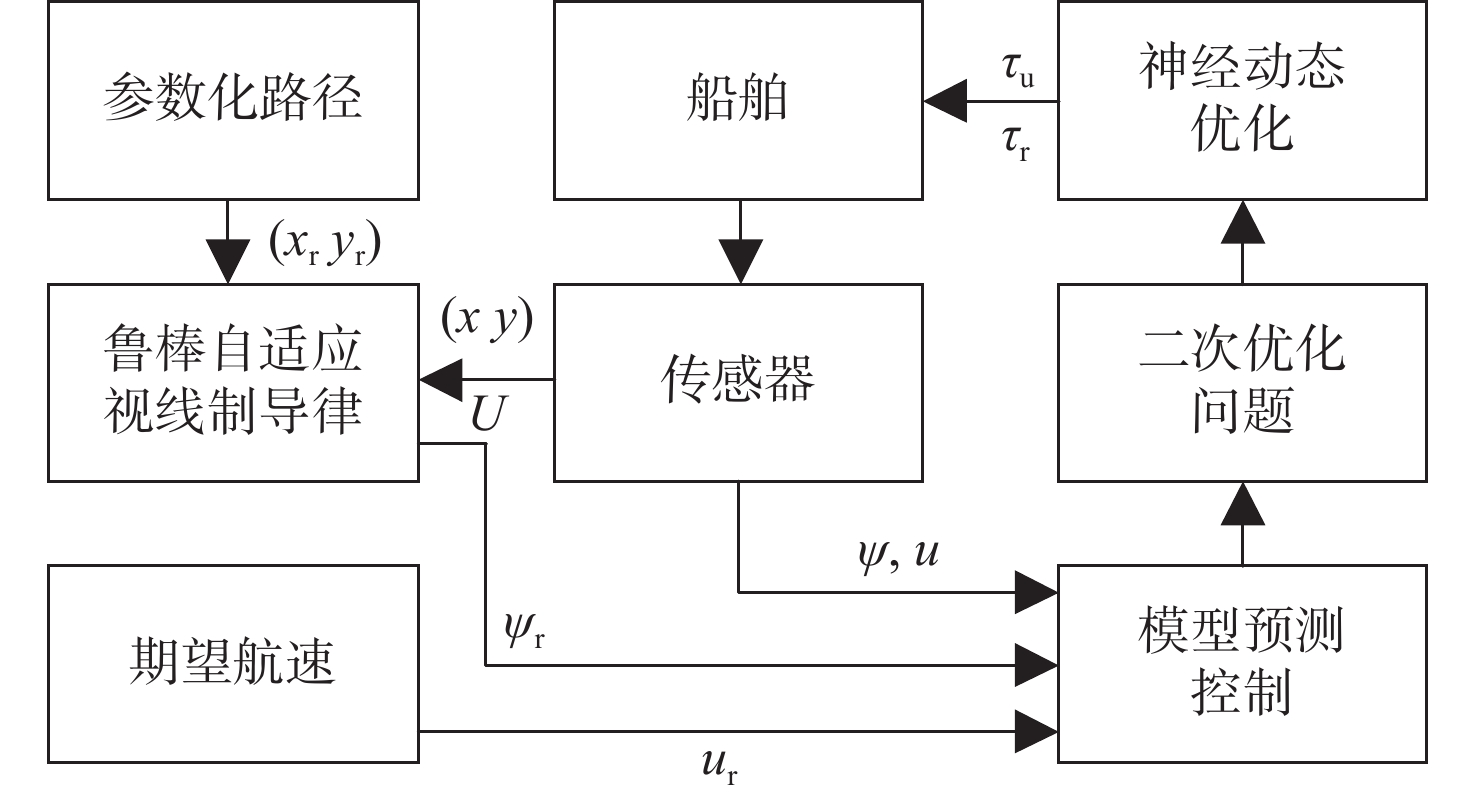
综合神经动态优化与模型预测控制方法的欠驱动船舶路径跟踪结构框架如图3所示。鲁棒自适应视线制导律获取参数化路径和传感器反馈的状态信息，输出期望航向角。模型预测控制获取期望航向角、期望航速和传感器反馈的状态信息，将路径跟踪问题转化为含有输入约束限制的二次优化问题。神经动态优化求解器并行地求解含有输入约束限制的二次优化问题，输出推进力和转艏力矩。推进力和转艏力矩作用于船舶，更新状态信息，构成闭环控制回路。
![]()
图 3 欠驱动船舶精确路径跟踪示意图Figure 3. Schematic diagram of the precise path following for the underactuated ship2. 制导律设计
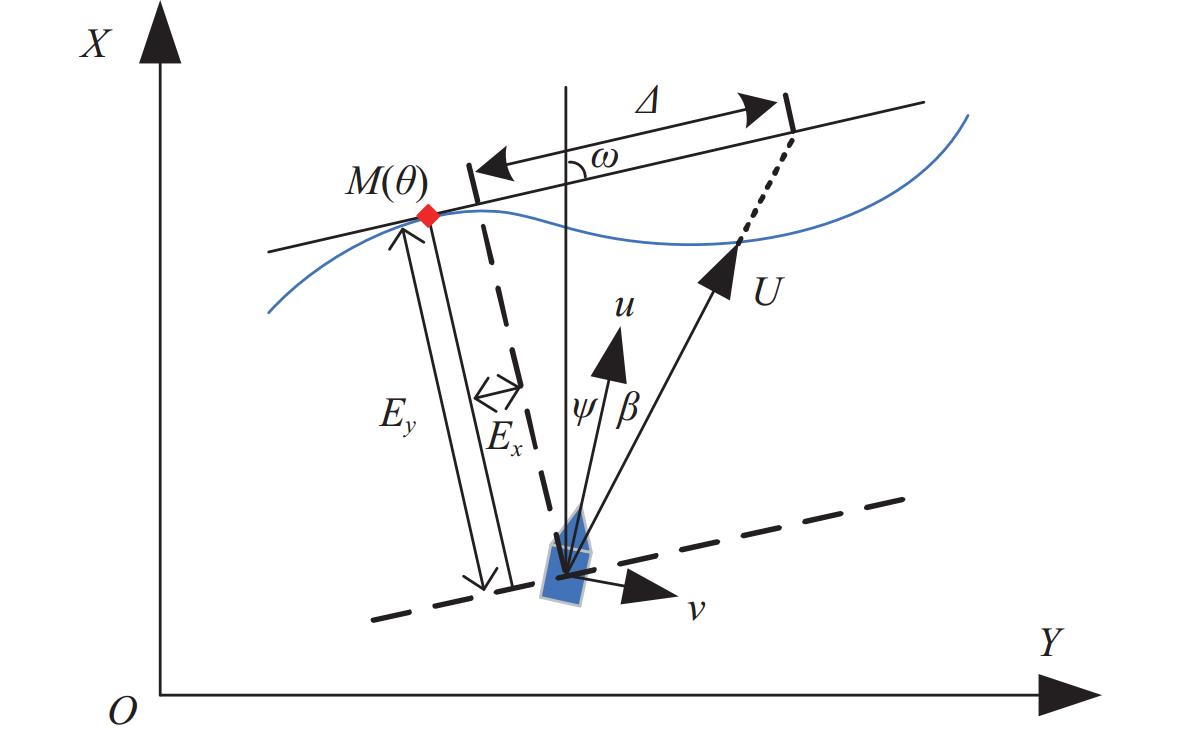
本部分将设计一种鲁棒自适应视线制导律，以增强对模型不确定性的鲁棒性，并补偿侧滑角的影响。图4为RALOS几何示意图，参数化路径点为{\boldsymbol{M}}(\theta ) = \left[ {{x_{\rm{r}}}(\theta )\;}\;\;\;{{y_{\rm{r}}}(\theta )} \right]，\theta 为路径参数。
定义路径切向角为
\omega (\theta ) = a\tan 2({y'_{\rm{r}}}(\theta ),{x'_{\rm{r}}}(\theta )) (4) 式中：{y'_{\rm{r}}}(\theta ) = \dfrac{{\partial {y_{\rm{r}}}(\theta )}}{{\partial \theta }}；{x'_{\rm{r}}}(\theta ) = \dfrac{{\partial {x_{\rm{r}}}(\theta )}}{{\partial \theta }}。
参数化路径速度分量为：
\begin{split} & {{\dot x}_{\rm{g}}}(\theta ) = {{\boldsymbol{u}}_{\rm{p}}}\cos \omega \\& {{\dot y}_{\rm{g}}}(\theta ) = {{\boldsymbol{u}}_{\rm{p}}}\sin \omega \end{split} (5) 式中，{{\boldsymbol{u}}_{\rm{p}}}为虚拟速度输入。
路径跟踪纵向误差{E_x}、横向误差{E_y}分别为
\left[ \begin{matrix} {{E_x}} \\ {{E_y}} \end{matrix} \right] = {\left[ \begin{matrix} {\cos \omega }&{\; - \sin \omega } \\ {\sin \omega }&{\cos \omega } \end{matrix} \right]^{\rm{T}}}\left[ \begin{matrix} {x - {x_{\rm{r}}}} \\ {y - {y_{\rm{r}}}} \end{matrix} \right] (6) 对式（6）进行求导，得到路径跟踪误差动态表达式为：
\begin{split} & {{\dot E}_x} = u\cos (\psi - \omega ) - v\sin (\psi - \omega ) + \kappa + \dot \omega {E_y} - {{\boldsymbol{u}}_{\rm{p}}} \\& {{\dot E}_y} = u\sin (\psi - \omega ) + v\cos (\psi - \omega ) - \dot \omega {E_x} \end{split} (7) 式中，\kappa 为模型不确定性的影响，且\left| \kappa \right| \leqslant \vartheta ，\vartheta 为设计参数。
设计参考航向角{\psi _{\rm{r}}}[13]，并根据自适应控制理论中参数估计的思想，对侧滑角进行估计：
\begin{split} & \psi_{\rm{r}}=\omega-\mathrm{arctan}\left(\frac{E_y}{\mathit{\Delta}}\right)-\hat{\beta} \\ &\dot{\hat{\beta}}=\sigma U\left(\frac{\mathit{\Delta}E_y}{\sqrt{\mathit{\Delta}^2+E_y^2}}+\frac{E_xE_y}{\sqrt{\mathit{\Delta}^2+E_y^2}}\right) \end{split} (8) 式中：\hat \beta 为侧滑角估计值；\sigma 为自适应参数；\varDelta 为前视距离。
在路径跟踪动态表达式中，引入侧滑角的影响：
\begin{split} & \dot{E}_x=U\left(\frac{\mathit{\Delta}}{\sqrt{E_y^2+\mathit{\Delta}^2}}+\frac{E_y}{\sqrt{E_y^2+\mathit{\Delta}^2}}\tilde{\beta}\right)+\kappa+\dot{\omega}E_y-\boldsymbol{u}_{\rm{p}} \\ &\dot{E}_y=U\left(-\frac{E_y}{\sqrt{E_y^2+\mathit{\Delta}^2}}+\frac{\mathit{\Delta}}{\sqrt{E_y^2+\mathit{\Delta}^2}}\tilde{\beta}\right)-\dot{\omega}E_x \end{split} (9) 式中：U为船舶合速度，U = \sqrt {{u^2} + {v^2}} ；\beta 为侧滑角，\beta = a\tan 2(v,u)；\tilde \beta 为侧滑角的估计误差，\tilde \beta = \beta - \hat \beta 。
为验证制导系统稳定性，构造李雅普诺夫函数为
V = \frac{1}{2}{E_x}^2 + \frac{1}{2}{E_y}^2 + \frac{1}{{2\sigma }}{\tilde \beta ^2} \geqslant 0 (10) 对李雅普诺夫函数求导，
\dot V = {E_x}{\dot E_x} + {E_y}{\dot E_y} + \frac{1}{\sigma }\tilde \beta \dot {\tilde \beta} (11) 式中，\dot {\tilde \beta} = - \dot {\hat \beta} ，并且\sigma > 0。
将式（9）代入式（11），得
\begin{gathered}\dot{V}=E_y\left[U\left(-\frac{E_y}{\sqrt{E_y^2+\Delta^2}}+\frac{\mathit{\Delta}}{\sqrt{E_y^2+\mathit{\Delta}^2}}\tilde{\beta}\right)-\dot{\omega}E_x\right]+ \\ E_x\left[U\left(\frac{\mathit{\Delta}}{\sqrt{E_y^2 + \mathit{\Delta}^2}} + \frac{E_y}{\sqrt{E_y^2 + \mathit{\Delta}^2}}\tilde{\beta}\right) + \kappa + \dot{\omega}E_y - \boldsymbol{u}_{\rm{p}}\right]-\frac{1}{\sigma}\tilde{\beta}\dot{\hat{\beta}}\end{gathered} (12) 根据滑模的思想，设计虚拟速度输入[13]
\boldsymbol{u}_{\rm{p}}=U\frac{\mathit{\Delta}}{\sqrt{E_y^2+\mathit{\Delta}^2}}+\lambda E_x+\gamma\left[\rm{sign}(E_x)\right] (13) 式中：\lambda > 0和\gamma > 0为设计参数；{\rm{sign}}( \cdot )为符号函数。
将式（8）与式（13）代入式（12）中，可得
\begin{split} & \dot{V}=-U\frac{E_y^2}{\sqrt{E_y^2+\mathit{\Delta}^2}}-\lambda E_x^2-\gamma\left|E_x\right|+E_x\kappa\leqslant \\ &\quad-U\frac{E_y^2}{\sqrt{E_y^2+\mathit{\Delta}^2}}-\lambda E_x^2-\gamma\left|E_x\right|+\left|E_x\vartheta\right| \end{split} (14) 令\gamma \geqslant \vartheta > 0，由式（14）可得
\dot{V}\leqslant-U\frac{E_y^2}{\sqrt{E_y^2+\mathit{\Delta}^2}}-\lambda E_x^2-(\gamma-\vartheta)\left|E_x\right|\leqslant0 (15) 因此，由李雅普诺夫稳定性定理可得出该系统有界。
3. 控制器设计
本部分将基于投影递归神经网络提出一种综合神经动态优化与模型预测控制方法，以实现欠驱动船舶路径跟踪，并提升模型预测控制的计算效率。
控制设计模型为：
\begin{split} & \dot u = - \frac{{{d_{11}}}}{{{m_{11}}}}u + \frac{1}{{{m_{11}}}}{\tau _{\rm{u}}} \\& \dot \psi = r \\& \dot r = - \frac{{{d_{33}}}}{{{m_{33}}}}r + \frac{1}{{{m_{33}}}}{\tau _{\rm{r}}} \end{split} (16) 在式（16）的基础上，构造状态空间模型：
\begin{split} & {{\dot {\boldsymbol{x}}}_{\rm{c}}} = {{\boldsymbol{A}}_{\rm{c}}}{{\boldsymbol{x}}_{\rm{c}}} + {{\boldsymbol{B}}_{\rm{c}}}{{\boldsymbol{u}}_{\rm{c}}} \\&\quad\;\; {{\boldsymbol{y}}_{\rm{c}}} = {{\boldsymbol{C}}_{\rm{c}}}{{\boldsymbol{x}}_{\rm{c}}} \end{split} (17) 其中：
\boldsymbol{x}_{\rm{c}}=\left[\begin{matrix}u \\ \psi \\ r\end{matrix}\right]_{3\times1}， A_{\rm{c}}=\left[\begin{matrix}-\dfrac{d_{11}}{m_{11}}\; & 0 & \; 0 \\ 0\; & 0 & \; 1 \\ 0\; & 0 & \; -\dfrac{d_{33}}{m_{33}}\end{matrix}\right]_{3\times3} B_{\rm{c}} = \left[\begin{matrix}\dfrac{1}{m_{11}} & 0 \\ 0 & 0 \\ 0 & \dfrac{1}{m_{33}}\end{matrix}\right]_{3\times2} ， \boldsymbol{C}_{\rm{c}} = \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0\end{matrix}\right]_{2\times3} ， \boldsymbol{ u}_{\rm{c}} = \left[\begin{matrix}\tau_{\rm{u}} & \tau_{\rm{r}}\end{matrix}\right]_{2\times1}^{\mathrm{T}} 确定采样间隔，将状态空间模型进行离散化处理，可得
\begin{split} & {{\boldsymbol{x}}_{\rm{m}}}(k + 1) = {{\boldsymbol{A}}_{\rm{m}}}{{\boldsymbol{x}}_{\rm{m}}}(k) + {{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k) \\& {{\boldsymbol{y}}_{\rm{m}}}(k) = {{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{x}}_{\rm{m}}}(k) \end{split} (18) 对于状态变量的预测可以用当前状态变量和未来{N_{\rm{c}}}时刻控制输入来表示：
\begin{split} & \qquad{{\boldsymbol{x}}_{\rm{m}}}(k + 1|k) = {{\boldsymbol{A}}_{\rm{m}}}{{\boldsymbol{x}}_{\rm{m}}}(k) + {{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k) \\& {{\boldsymbol{x}}_{\rm{m}}}(k + 2|k) = {{\boldsymbol{A}}_{\rm{m}}}{{\boldsymbol{x}}_{\rm{m}}}(k + 1|k) + {{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k + 1) =\\&\quad {{\boldsymbol{A}}_{\rm{m}}}^2{{\boldsymbol{x}}_{\rm{m}}}(k) + {{\boldsymbol{A}}_{\rm{m}}}{{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k) + {{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k + 1) \end{split} (19) \begin{split} & \qquad\qquad\qquad\qquad\quad\vdots \\& {{\boldsymbol{x}}_{\rm{m}}}(k + {N_{\rm{p}}}|k) = {{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}}}{{\boldsymbol{x}}_{\rm{m}}}(k) + {{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - 1}{{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k) + \cdots\\&\qquad\qquad {{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - {N_{\rm{c}}}}{{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k + {N_{\rm{c}}} - 1) \end{split} 式中：假设控制时域{N_{\rm{c}}}以外的{{\boldsymbol{u}}_{\rm{m}}} = 0[23]；{N_{\rm{p}}}为预测时域。一般而言，{N_{\rm{c}}} \leqslant {N_{\rm{p}}}。
对于输出变量的预测表示为
\begin{split} & \qquad\quad{{\boldsymbol{y}}_{\rm{m}}}(k + 1|k) = {{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}{{\boldsymbol{x}}_{\rm{m}}}(k) + {{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k) \\& \qquad\qquad\qquad\qquad\qquad \vdots\\& {{\boldsymbol{y}}_{\rm{m}}}(k + {N_{\rm{p}}}|k) = {{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}}}{{\boldsymbol{x}}_{\rm{m}}}(k) + {{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - 1}{{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k) + \cdots\\&\qquad\qquad {{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - {N_{\rm{c}}}}{{\boldsymbol{B}}_{\rm{m}}}{{\boldsymbol{u}}_{\rm{m}}}(k + {N_{\rm{c}}} - 1) \end{split} (20) 定义预测输出向量Y和控制输入向量 \mathbf{\mathit{\varsigma}} ：
\begin{split} & {\boldsymbol{Y}} = {\left[ {{{\boldsymbol{y}}_{\rm{m}}}{{(k + 1)}^{\rm{T}}}\;}\;\;\;{{{\boldsymbol{y}}_{\rm{m}}}{{(k + 2)}^{\rm{T}}}\;} \;\;\;{ \cdots \;}\;\;\;{{{\boldsymbol{y}}_{\rm{m}}}{{(k + {N_{\rm{p}}})}^{\rm{T}}}} \right]^{\rm{T}}}_{2{N_{\rm{p}}} \times 1} \\& {\boldsymbol{\varsigma}} = {\left[ \ {{{\boldsymbol{u}}_{\rm{m}}}{{(k)}^{\rm{T}}}\;}\;\;\;{{{\boldsymbol{u}}_{\rm{m}}}{{(k + 1)}^{\rm{T}}}\;} \;\;\;{ \cdots \;}\;\;\;{{{\boldsymbol{u}}_{\rm{m}}}{{(k + {N_{\rm{c}}} - 1)}^{\rm{T}}}}\right]^{\rm{T}}}_{2{N_{\rm{c}}} \times 1} \end{split} (21) Y可以用{{\boldsymbol{x}}_{\rm{m}}}(k)和\varsigma 表示为
{\boldsymbol{Y}} = {\boldsymbol{F}}{{\boldsymbol{x}}_{\rm{m}}}(k) + {\boldsymbol{\phi}} \varsigma (22) 其中，F和{\boldsymbol{\phi }}分别为
{\boldsymbol{F}} = {\left[ \begin{matrix} {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}} \\ {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^2} \\ {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^3} \\ \vdots \\ {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}}}} \end{matrix} \right]_{2{N_{\rm{p}}} \times 3}} {\boldsymbol{\phi}} = {\left[ \begin{matrix} {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{B}}_{\rm{m}}}} & 0 & \cdots & 0 \\ {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}{{\boldsymbol{B}}_{\rm{m}}}} & {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{B}}_{\rm{m}}}} & \vdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - 1}{{\boldsymbol{B}}_{\rm{m}}}} & {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - 2}{{\boldsymbol{B}}_{\rm{m}}}} & \cdots & {{{\boldsymbol{C}}_{\rm{m}}}{{\boldsymbol{A}}_{\rm{m}}}^{{N_{\rm{p}}} - {N_{\rm{c}}}}{{\boldsymbol{B}}_{\rm{m}}}} \end{matrix} \right]_{2{N_{\rm{p}}} \times 2{N_{\rm{c}}}}} 参考信号
{{\boldsymbol{R}}_{\rm{r}}}(k) = {\left[ \begin{matrix} {{{\boldsymbol{r}}_{\rm{r}}}(k)\;}&{{{\boldsymbol{r}}_{\rm{r}}}(k)\;}&{ \cdots \;}&{{{\boldsymbol{r}}_{\rm{r}}}(k)} \end{matrix} \right]^{\rm{T}}}_{2{N_{\rm{p}}} \times 1} (23) 式中，{{\boldsymbol{r}}_{\rm{r}}}(k) = [\begin{array}{*{20}{c}} {{\psi _{\rm{r}}}(k)\;}&{{{\boldsymbol{u}}_{\rm{r}}}(k)} \end{array}]，其中{\psi _{\rm{r}}}和{{\boldsymbol{u}}_{\rm{r}}}分别为参考航向角和参考航速。
定义代价函数
J = {\left( {{{\boldsymbol{R}}_{\rm{r}}} - {\boldsymbol{Y}}} \right)^{\rm{T}}}{\boldsymbol{Q}}\left( {{{\boldsymbol{R}}_{\rm{r}}} - {\boldsymbol{Y}}} \right) + {\varsigma ^{\rm{T}}}{\boldsymbol{R}}\varsigma (24) 式中，Q和R为权重矩阵。若{\boldsymbol{Q}}/{\boldsymbol{R}}值较大，表示控制器通过激进的控制动作使得系统状态能够快速地收敛。
{\boldsymbol{Q}} = {{\boldsymbol{I}}_{{N_{\rm{p}}} \times {N_{\rm{p}}}}} \otimes \left[ \begin{matrix} {{q_1}\;}&0 \\ {0\;}&{{q_2}} \end{matrix} \right]\text{，} {\boldsymbol{R}} = {{\boldsymbol{I}}_{{N_{\rm{c}}} \times {N_{\rm{c}}}}} \otimes \left[ \begin{matrix} {{r_1}\;}&0 \\ {0\;}&{{r_2}} \end{matrix} \right] 式中：{q_j},{{\boldsymbol{r}}_j},j = 1,2为权重调整参数； \otimes 表示Kronecker积。
神经动态优化求解器利用投影递归神经网络的并行求解架构，对代价函数J进行优化求解，进而提升计算效率。根据李雅普诺夫稳定性理论，可得出投影递归神经网络有界的结论[19-20]。因此，神经动态优化求解器可以收敛于平衡点，该平衡点对应于二次优化问题的最优解。
将式（22）代入式（24）中，对代价函数J进行展开，可得
\begin{gathered} J = {\varsigma ^{\rm{T}}}({{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{Q}}{\boldsymbol{\phi}} + {\boldsymbol{R}})\varsigma + {\varsigma ^{\rm{T}}}({{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{QF}}{{\boldsymbol{x}}_{\rm{m}}} - {{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{Q}}{{\boldsymbol{R}}_{\rm{r}}}) +\\ ({{\boldsymbol{x}}_{\rm{m}}}^{\rm{T}}{{\boldsymbol{F}}^{\rm{T}}}{\boldsymbol{Q}}{\boldsymbol{\phi}} - {{\boldsymbol{R}}_{\rm{r}}}^{\rm{T}}{\boldsymbol{Q}}{\boldsymbol{\phi}} )\varsigma + \left( {{{\boldsymbol{x}}_{\rm{m}}}^{\rm{T}}{{\boldsymbol{F}}^{\rm{T}}} - {{\boldsymbol{R}}_{\rm{r}}}^{\rm{T}}} \right){\boldsymbol{Q}}({\boldsymbol{F}}{{\boldsymbol{x}}_{\rm{m}}} - {{\boldsymbol{R}}_{\rm{r}}}) \end{gathered} (25) 将J对\varsigma 求导，可得
\nabla {\boldsymbol{J}} = 2({{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{Q}}{\boldsymbol{\phi}} + R)\varsigma + 2({{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{QF}}{{\boldsymbol{x}}_{\rm{m}}} - {{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{Q}}{{\boldsymbol{R}}_{\rm{r}}}) (26) 将式（24）视为二次优化问题，基于投影递归神经网络建立神经动态优化求解器
\dot \varsigma = \iota ({{\boldsymbol{P}}_{\rm{X}}}(\varsigma - \nabla {\boldsymbol{J}}) - \varsigma ) (27) 投影算子降低了网络复杂度，简化了约束条件的处理过程，其公式表达为
{P_{\rm{X}}}(f({\varsigma _i})) = \left\{ \begin{aligned} & {d_{\max }},&& {f({\varsigma _i}) \geqslant {d_{\max }}} \\ & {f({\varsigma _i})},&& {{d_{\min }} < f({\varsigma _i}) < {d_{\max }}} \\ & {d_{\min }}, &&{f({\varsigma _i}) \leqslant {d_{\min }}} \end{aligned}\right. (28) 式中：i = 1,2, \cdots 2{N_{\rm{c}}}；f({\varsigma _i}) = {\varsigma _i} - \nabla {J_i}。
因此，神经动态优化求解器可以通过迭代来求解代价函数J的最优解序列，并提升计算效率。然后，选取最优解序列\varsigma 的第一个元素，作用于系统，刷新系统状态，以达到模型预测控制滚动优化的目的。
4. 仿真实验
为验证RALOS制导律与模型预测控制相结合的可行性，本部分采用CyberShip Ⅱ[22]进行路径跟踪仿真实验。在实验中，{\tau _{\rm{u}}}为船舶纵向推力，其数值被约束在\left| {{\tau _{\rm{u}}}} \right| \leqslant 2 N；{\tau _{\rm{r}}}为船舶转艏力矩，其数值被约束在\left| {{\tau _{\rm{r}}}} \right| \leqslant 1.5 N·m。为验证在模型预测控制中引入神经动态优化求解器后提升计算效率方面的优势，本部分的仿真实验统一采用Intel （R） I7-8700 3.20 GHz处理器，在确保船舶模型和制导律一致的前提下，将本文提出的神经动态优化求解器与文献[13]中的Fmincon优化求解器（MATLAB内置求解器）进行对比，仿真实验中主要系统参数如表1所示。完整的欠驱动船舶路径跟踪系统包括导航、制导和控制部分。本文针对制导和控制部分进行研究，提出鲁棒自适应视线制导律和具有实时性的欠驱动船舶路径跟踪预测控制器。仿真实验过程的具体步骤如下：
表 1 仿真实验主要参数Table 1. Main parameters for simulation experiments系统类型 参 数 制导律 \mathit{\Delta}=4 \lambda = 10 \gamma = 0.001 \sigma=0.000\ 1 控制器 {N_{\rm{p}}} = 40 {N_{\rm{c}}} = 20 {\boldsymbol{Q}} = {{\boldsymbol{I}}_{{N_{\rm{p}}} \times {N_{\rm{p}}}}} \otimes \left[ \begin{matrix} {100\;}&0 \\ {0\;}&1 \end{matrix} \right] {\boldsymbol{R}} = {{\boldsymbol{I}}_{{N_{\rm{c}}} \times {N_{\rm{c}}}}} \otimes \left[ \begin{matrix} {0.1\;}&0 \\ {0\;}&{0.1} \end{matrix} \right] 1） 导航部分：建立船舶运动数学模型模拟船舶的运动状态，获取所需的船舶状态信息。用这一过程在仿真实验中替代传感器的直接测量。
2） 制导部分：在路径规划方面，预先设定参数化路径点。采用鲁棒自适应视线制导律获取参数化路径点和反馈的船舶状态信息，输出期望航向角。
3） 控制部分：采用模型预测控制获取期望航向角、期望航速和反馈的船舶状态信息，将路径跟踪问题转化为含有输入约束限制的二次优化问题。神经动态优化求解器并行求解含有输入约束限制的二次优化问题，输出推进力和转艏力矩。
4.1 直线路径跟踪
直线路径跟踪仿真实验中主要参数配置为：采样间隔 T_{\mathrm{s}} = 0.1 s；期望航速{u_{{\mathrm{ref}}}} = 0.3 m/s；神经网络参数\iota = 0.1；起始位置设定为\left( 0\;\;30 \right)和\left( 0\;\;70\right)；初始速度为0 m/s；初始航向为{0^\circ }。
参数化路径选择为
\begin{split} & {x_{\rm{r}}}(\theta ) = {x_0} + \theta \cos \alpha \\& {y_{\rm{r}}}(\theta ) = {y_0} + \theta \sin \alpha \end{split} (29) 式中：\theta 为路径参数；\dot \theta = \dfrac{{{u_{\rm{p}}}}}{{\sqrt {{{x'}_{\rm{r}}}^2(\varepsilon ) + {{y'}_{\rm{r}}}^2(\varepsilon )} }}； {x_0} = 0 ； {y_0} = 50 ；\alpha = {0^ \circ }。
参考速度设定为{\dot u_{\rm{r}}} = \dfrac{{{u_{{\mathrm{ref}}}} - {u_{\rm{r}}}}}{T}，T = 20。
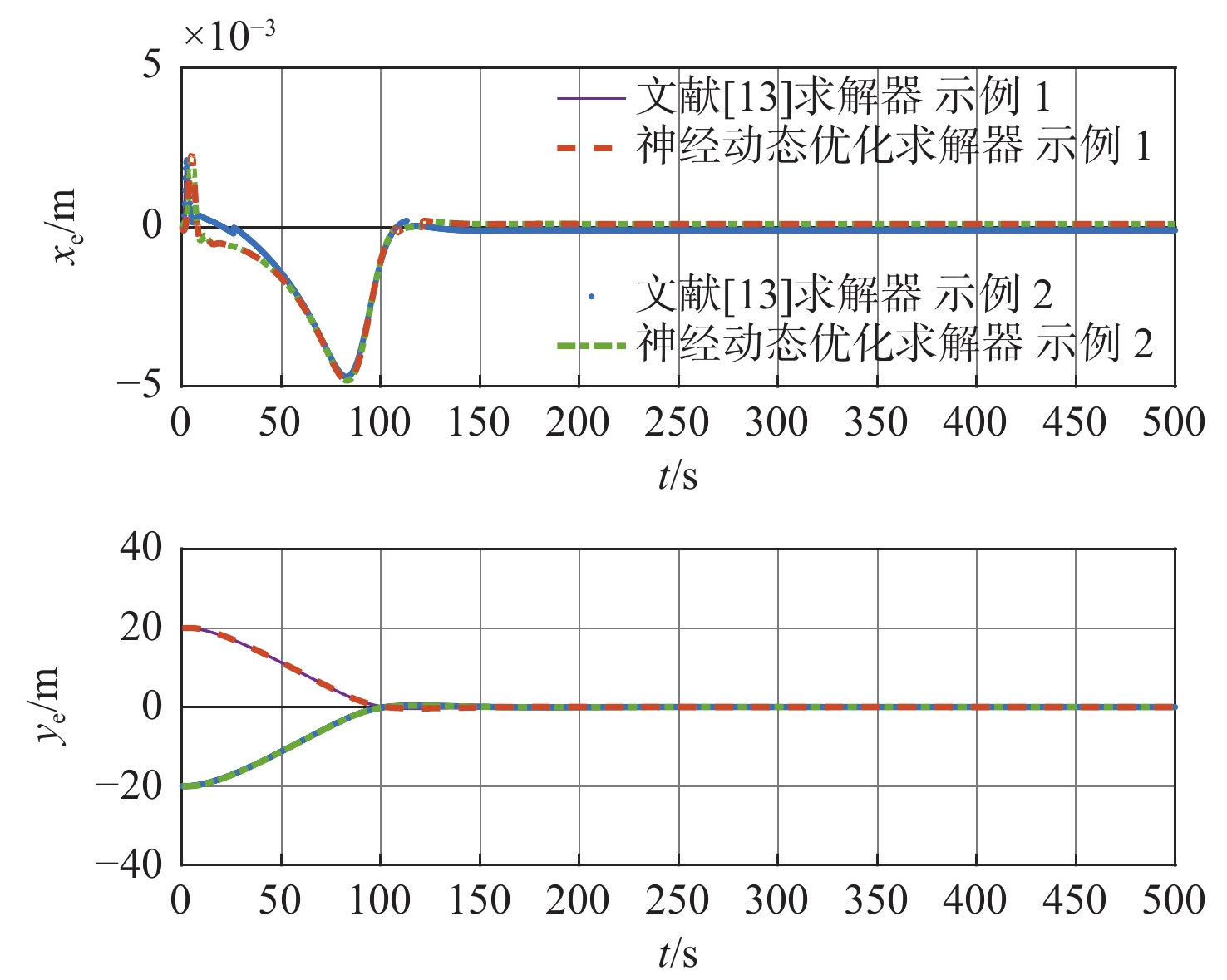
图5～图7为RALOS制导律结合模型预测控制分别采用本文提出的神经动态优化求解器与文献[13]中的Fmincon优化求解器的直线路径跟踪效果对比图。图5表明RALOS制导律结合模型预测控制分别采用的2种优化求解器均能使船舶较好地收敛于期望路径。图6为纵向和横向跟踪误差的变化情况，结果表明，在2种优化求解器作用下，路径跟踪误差均能较快地收敛至零附近。
![]()
图 5 欠驱动船舶直线路径跟踪对比图Figure 5. Comparison diagram of straight line path following for the underactuated ship![]()
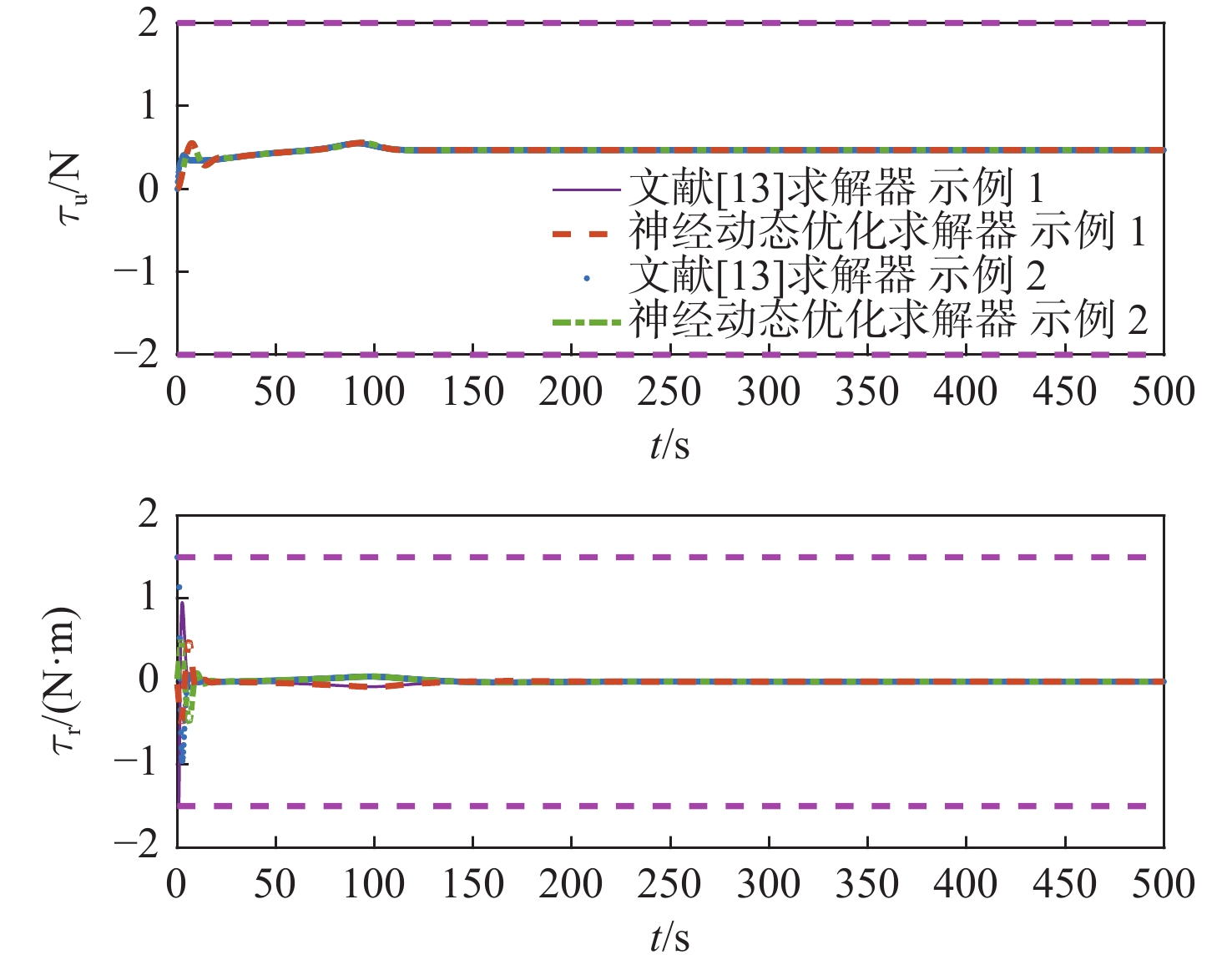
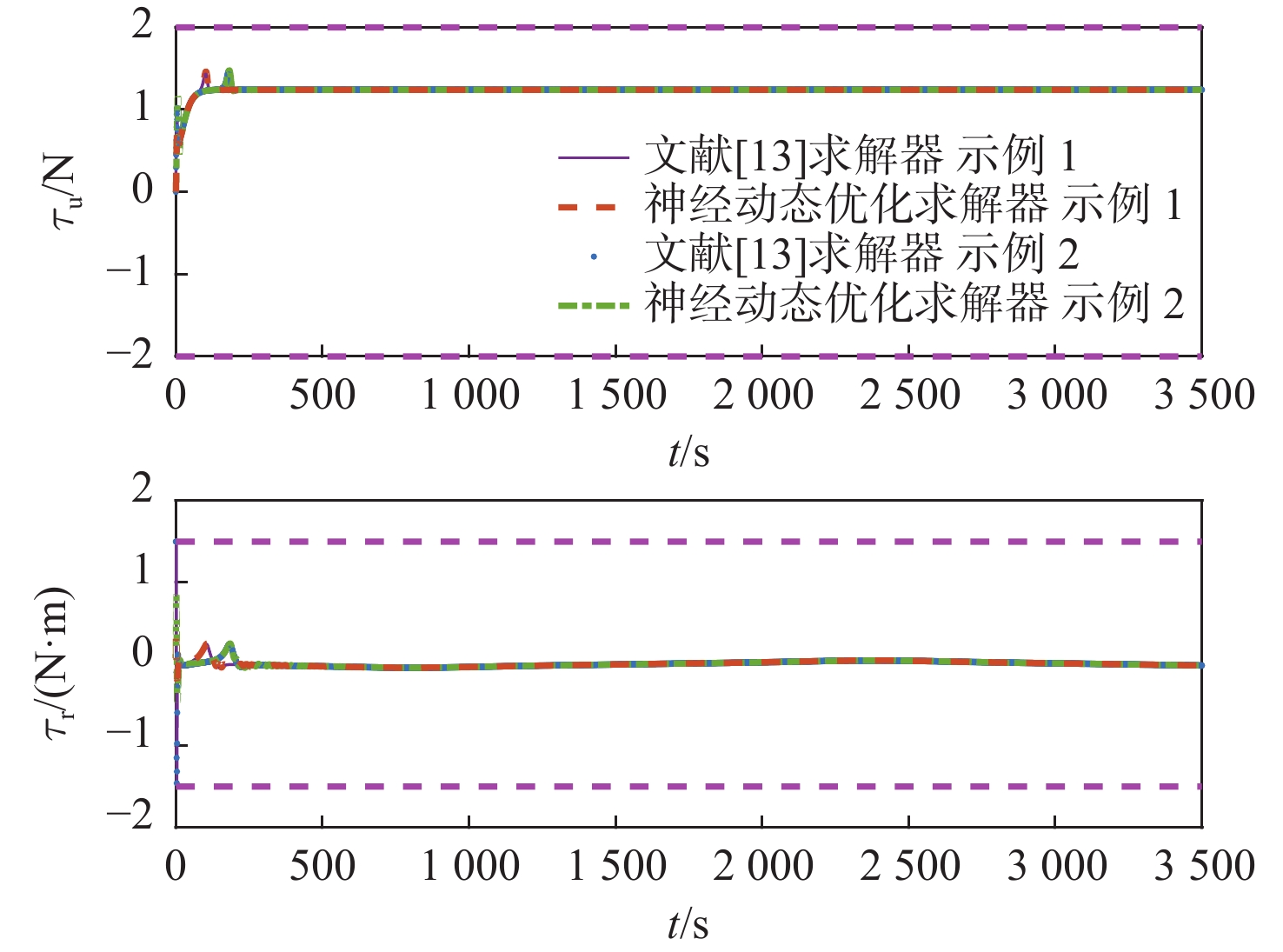
图 6 欠驱动船舶直线路径跟踪误差对比图Figure 6. Comparison diagram of tracking errors of straight line path following for the underactuated ship图7所示为直线路径跟踪的控制输入变化情况，2种优化求解器得到的解，趋势相近且均趋于平滑，并严格符合控制输入的约束限制。因此，RALOS制导律结合模型预测控制能够较好地实现欠驱动船舶直线路径跟踪。
![]()
图 7 欠驱动船舶直线路径跟踪控制输入对比图Figure 7. Comparison diagram of control inputs of straight line path following for the underactuated ship分析图5～图7可知，在直线路径跟踪过程中，神经动态优化求解器可以实现与Fmincon求解器相同的功能。表2展示了分别采用本文提出的神经动态优化求解器与文献[13]中的Fmincon优化求解器下的直线路径跟踪计算效率对比。在完成相同采样次数的前提下，船舶分别从不同起始点 \left(0\;\;30\right) 和\left( 0\;\;70 \right)出发，神经动态优化求解器较Fmincon求解器计算效率分别提升92.2和89.7倍。显然，神经动态优化求解器相较于Fmincon求解器具有显著的效率优势。
表 2 欠驱动船舶直线路径跟踪计算时间Table 2. Calculation time of straight line path following for underactuated ship工况 起始点 Fmincon
求解器[13]/s神经动态优化
求解器/s直线路径跟踪 \left( 0\;\;30 \right) 239.8 2.6 \left(0\;\;70 \right) 242.1 2.7 4.2 曲线路径跟踪
曲线路径跟踪仿真实验中主要参数配置为：采样间隔 T_{\mathrm{s}} =0.1 s；船舶起始位置分别设定为\left( 0\;\;50\right)和\left( 0\;\;100\right)；期望航速{u_{{\mathrm{ref}}}} = 0.5 m/s；神经网络参数\iota = 0.1；初始速度为0 m/s；初始航向为{0^\circ }。
参数化路径选择为：
\begin{gathered} {x_{\rm{r}}}(\theta ) = {x_0} + \xi \theta \\ {y_{\rm{r}}}(\theta ) = {y_0} + \delta \sin \theta \\ \end{gathered} (30) 式中：\theta 为路径参数；\dot \theta = \dfrac{{{u_{\rm{p}}}}}{{\sqrt {{{x'}_{\rm{r}}}^2(\varepsilon ) + {{y'}_{\rm{r}}}^2(\varepsilon )} }}； {x_0} = 0 ； {y_0} = 0 ；\xi = 100；\delta = 160。
参考速度设定为 {\dot u_{\rm{r}}} = \dfrac{{{u_{{\mathrm{ref}}}} - {u_{\rm{r}}}}}{T} ，T = 20。
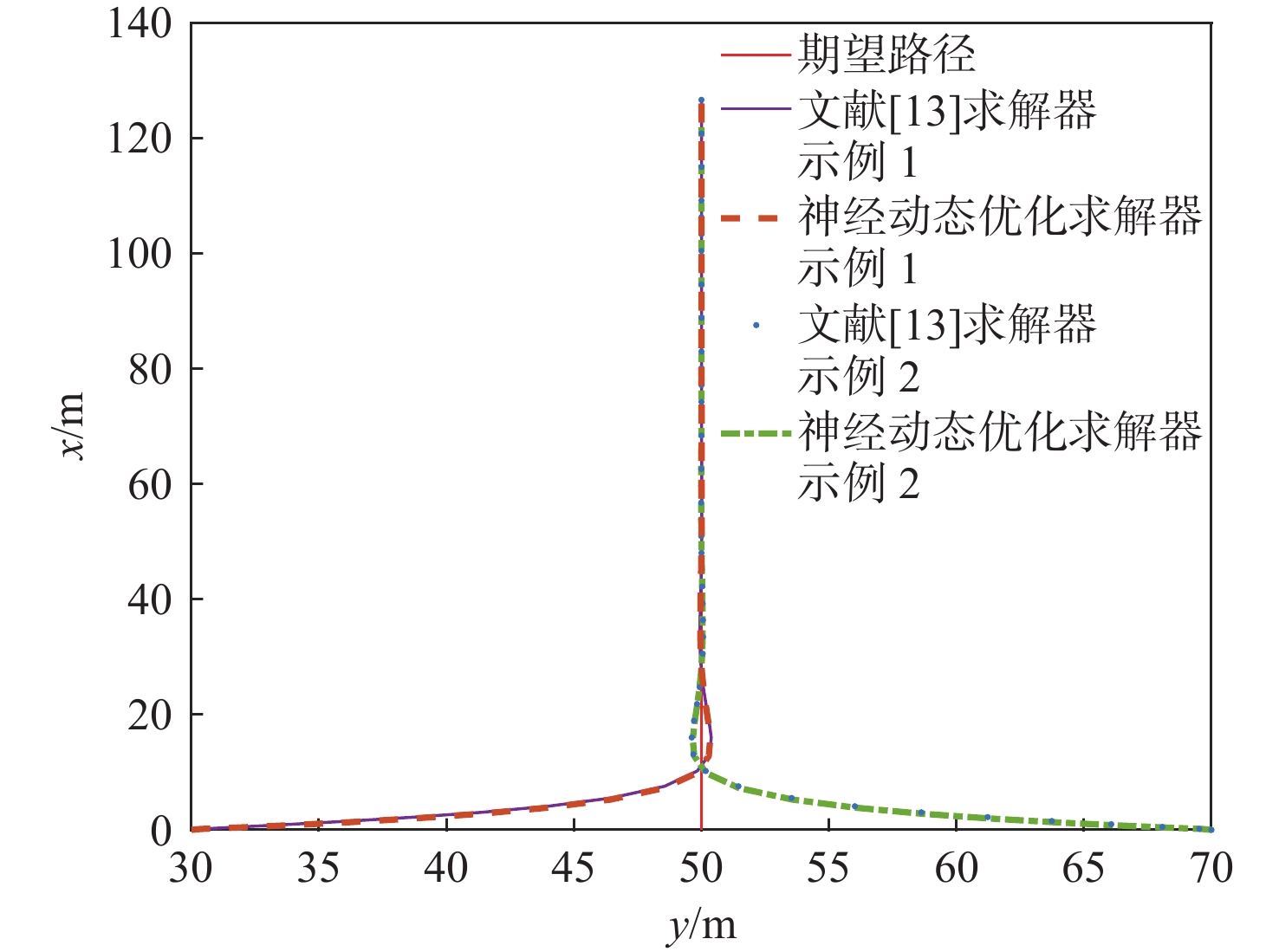
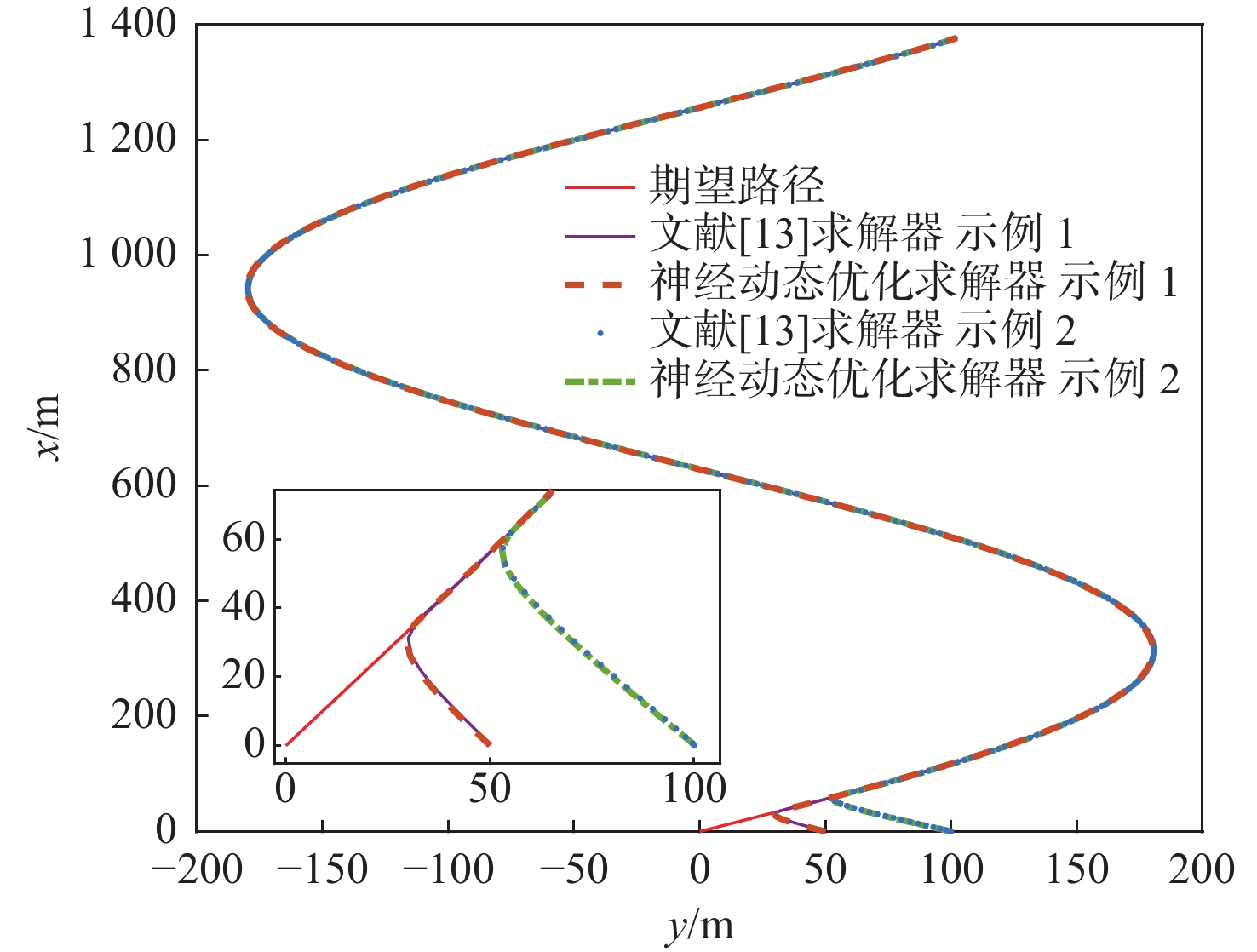
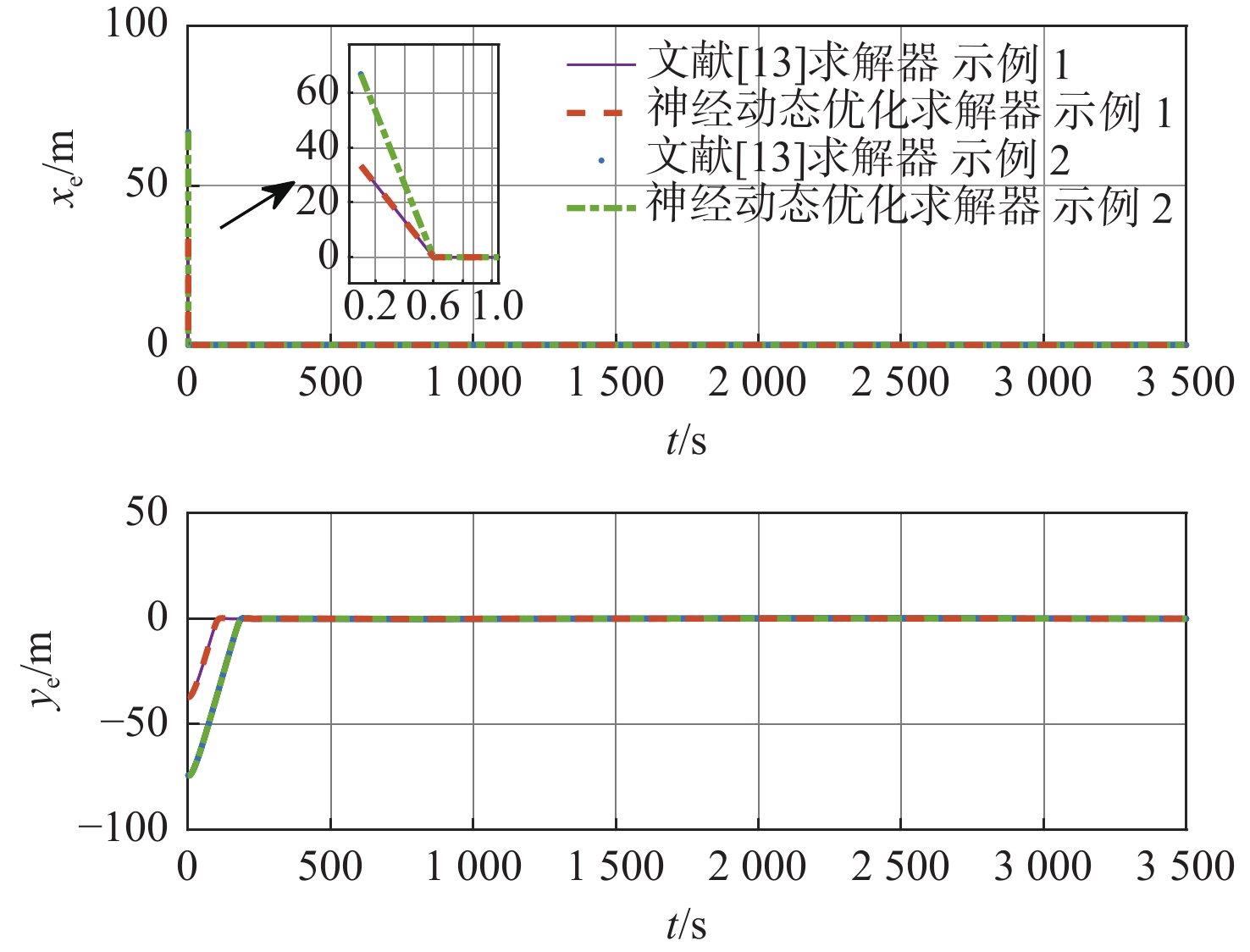
图8～图10是RALOS制导律结合模型预测控制分别采用本文提出的神经动态优化求解器与文献[13]中的Fmincon求解器下的曲线路径跟踪效果对比。图8展示了船舶在2种优化求解器下均能较好地收敛至参考路径。图9表明RALOS制导律与模型预测控制相结合，应用2种优化求解器时，得到的跟踪误差均能较快收敛至零附近。图10为曲线路径跟踪的控制输入情况，2种优化求解器得到的控制输入趋势相近且平滑，并严格满足控制输入的约束限制。因此，RALOS制导律结合模型预测控制可较好地实现欠驱动船舶的曲线路径跟踪。
![]()
图 8 欠驱动船舶曲线路径跟踪对比图Figure 8. Comparison diagram of curved line path following for the underactuated ship![]()
图 9 欠驱动船舶曲线路径跟踪误差对比图Figure 9. Comparison diagram of tracking errors of curved line path following for underactuated ship![]()
图 10 欠驱动船舶曲线路径跟踪控制输入对比图Figure 10. Comparison diagram of control inputs of curved line path following for underactuated ship分析图8～图10可知，在曲线路径跟踪过程中，神经动态优化求解器可以实现与Fmincon求解器相同的功能。表3为分别采用本文提出的神经动态优化求解器与文献[13]中的Fmincon优化求解器求得曲线路径跟踪计算效率的对比。在完成相同采样次数的前提下，船舶分别从不同起始点\left( 0\;\;50 \right)和\left( 0\;\;100 \right)出发，神经动态优化求解器较Fmincon求解器计算效率分别提升96.2和96倍。结果表明，在曲线路径跟踪中，神经动态优化求解器在计算效率方面明显优于Fmincon求解器。
表 3 欠驱动船舶曲线路径跟踪计算时间Table 3. Calculation time of curved line path following for the underactuated ship工况 起始点 Fmincon
求解器[13]/s神经动态优化
求解器/s曲线路径跟踪 \left(0\;\;50\right) 1 858 19.3 \left( 0\;\;100 \right) 1 805 18.8 5. 结 语
传统模型预测控制方法采用在线滚动方式进行优化求解，导致欠驱动船舶路径跟踪预测控制器计算量大，因此，本文将神经动态优化系统引入模型预测控制方法，提出一种具有实时性的欠驱动船舶路径跟踪预测控制器。
在制导律方面，本文基于自适应控制理论和滑模的思想，提出鲁棒自适应视线制导律，提升了对模型不确定性的鲁棒性，并补偿侧滑角的影响。在控制器方面，基于投影递归神经网络，提出一种具有实时性的路径跟踪预测控制器，提升了计算效率。
结果表明，综合本文所提出的制导律和控制器，能够增强对模型不确定性的鲁棒性，补偿侧滑角影响，并提升路径跟踪预测控制的实时性能。所提方法相较于Fmincon求解器计算效率提升近90倍，可以实现任意路径跟踪目标。
本文研究成果为路径跟踪预测控制提供了更省时、更稳定的方法，同时也为提高模型预测控制的实时性能提供了新的思路。未来的研究工作将考虑将该方法拓展到多船协同预测控制中，以提升多船协同预测控制的实时性能。
-
![]()
图 3 欠驱动船舶精确路径跟踪示意图
Figure 3. Schematic diagram of the precise path following for the underactuated ship
![]()
图 5 欠驱动船舶直线路径跟踪对比图
Figure 5. Comparison diagram of straight line path following for the underactuated ship
![]()
图 6 欠驱动船舶直线路径跟踪误差对比图
Figure 6. Comparison diagram of tracking errors of straight line path following for the underactuated ship
![]()
图 7 欠驱动船舶直线路径跟踪控制输入对比图
Figure 7. Comparison diagram of control inputs of straight line path following for the underactuated ship
![]()
图 8 欠驱动船舶曲线路径跟踪对比图
Figure 8. Comparison diagram of curved line path following for the underactuated ship
![]()
图 9 欠驱动船舶曲线路径跟踪误差对比图
Figure 9. Comparison diagram of tracking errors of curved line path following for underactuated ship
![]()
图 10 欠驱动船舶曲线路径跟踪控制输入对比图
Figure 10. Comparison diagram of control inputs of curved line path following for underactuated ship
表 1 仿真实验主要参数
Table 1 Main parameters for simulation experiments
系统类型 参 数 制导律 \mathit{\Delta}=4 \lambda = 10 \gamma = 0.001 \sigma=0.000\ 1 控制器 {N_{\rm{p}}} = 40 {N_{\rm{c}}} = 20 {\boldsymbol{Q}} = {{\boldsymbol{I}}_{{N_{\rm{p}}} \times {N_{\rm{p}}}}} \otimes \left[ \begin{matrix} {100\;}&0 \\ {0\;}&1 \end{matrix} \right] {\boldsymbol{R}} = {{\boldsymbol{I}}_{{N_{\rm{c}}} \times {N_{\rm{c}}}}} \otimes \left[ \begin{matrix} {0.1\;}&0 \\ {0\;}&{0.1} \end{matrix} \right] 
下载: 导出CSV
-
[1] 张文拴, 李争, 郑瑶. 国内外无人船发展现状及研发趋势[J]. 舰船科学技术, 2024, 46(15): 79–83. doi: 10.3404/j.issn.1672-7649.2024.15.014 ZHANG W S, LI Z, ZHENG Y. The current status and research and development trend of unmanned ships at home and abroad[J]. Ship Science and Technology, 2024, 46(15): 79–83 (in Chinese). doi: 10.3404/j.issn.1672-7649.2024.15.014
[2] 刘程. 船舶路径跟踪与减横摇综合控制研究[D]. 上海: 上海交通大学, 2015. LIU C. Integrated control of path following and roll motion reduction for marine vessels[D]. Shanghai: Shanghai Jiaotong University, 2015 (in Chinese).
[3] 王浩亮, 尹晨阳, 卢丽宇, 等. 面向海上搜救的UAV与USV集群协同路径跟踪控制[J]. 中国舰船研究, 2022, 17(5): 157–165. doi: 10.19693/j.issn.1673-3185.02916 WANG H L, YIN C Y, LU L Y, et al. Cooperative path following control of UAV and USV cluster for maritime search and rescue[J]. Chinese Journal of Ship Research, 2022, 17(5): 157–165 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.02916
[4] PETTERSEN K Y, LEFEBER E. Way-point tracking control of ships[C]//Proceedings of the 40th IEEE Conference on Decision and Control (CDC 2001). Orlando: IEEE, 2001: 940–945.
[5] CAHARIJA W, PETTERSEN K Y, CALADO P, et al. A comparison between the ILOS guidance and the vector field guidance[J]. IFAC-PapersOnLine, 2015, 48(16): 89–94. doi: 10.1016/j.ifacol.2015.10.263
[6] WAN L L, SU Y X, ZHANG H J, et al. An improved integral light-of-sight guidance law for path following of unmanned surface vehicles[J]. Ocean Engineering, 2020, 205: 107302. doi: 10.1016/j.oceaneng.2020.107302
[7] 白一鸣, 刘磊, 韩新洁. 基于改进自适应积分视线制导方法的欠驱动无人水面艇路径跟踪控制[J]. 上海海事大学学报, 2021, 42(4): 12–19, 52. doi: 10.13340/j.jsmu.2021.04.003 BAI Y M, LIU L, HAN X J. Path following control for underactuated USVs based on improved adaptive integral line-of-sight guidance law[J]. Journal of Shanghai Maritime University, 2021, 42(4): 12–19, 52 (in Chinese). doi: 10.13340/j.jsmu.2021.04.003
[8] LIU L, WANG D, PENG Z H. ESO-based line-of-sight guidance law for path following of underactuated marine surface vehicles with exact sideslip compensation[J]. IEEE Journal of Oceanic Engineering, 2017, 42(2): 477–487. doi: 10.1109/JOE.2016.2569218
[9] FOSSEN T I. An adaptive line-of-sight (ALOS) guidance law for path following of aircraft and marine craft[J]. IEEE Transactions on Control Systems Technology, 2023, 31(6): 2887–2894. doi: 10.1109/TCST.2023.3259819
[10] 余亚磊, 苏荣彬, 冯旭, 等. 基于速变LOS的无人船反步自适应路径跟踪控制[J]. 中国舰船研究, 2019, 14(3): 163–171. doi: 10.19693/j.issn.1673-3185.01377 YU Y L, SU R B, FENG X, et al. Tracking control of backstepping adaptive path of unmanned surface vessels based on surge-varying LOS[J]. Chinese Journal of Ship Research, 2019, 14(3): 163–171 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.01377
[11] LIU C, GUO W L, SUN T. RLOS-based path following with event-triggered roll motion control for underactuated ship using rudder[J]. Ocean Engineering, 2023, 269: 113592. doi: 10.1016/j.oceaneng.2022.113592
[12] 徐双, 刘程, 郭玮丽. 基于鲁棒视线制导方法的欠驱动船舶路径跟踪[J]. 大连海事大学学报, 2024, 50(1): 20–27. doi: 10.16411/j.cnki.issn1006-7736.2024.01.003 XU S, LIU C, GUO W L. Underactuated ship path tracking based on robust line-of-sight guidance method[J]. Journal of Dalian Maritime University, 2024, 50(1): 20–27 (in Chinese). doi: 10.16411/j.cnki.issn1006-7736.2024.01.003
[13] SHI J Q, LIU C, SUN T, et al. Path following of underactuated ship using integral MPC and robust adaptive line-of-sight guidance[C]//2024 43rd Chinese Control Conference (CCC 2024). Kunming, China: IEEE, 2024: 4048−4054.
[14] 冯鑫, 于双和. 基于滑模预测控制的水面无人船轨迹跟踪研究[J]. 电光与控制, 2023, 30(9): 92–98. doi: 10.3969/j.issn.1671-637X.2023.09.016 FENG X, YU S H. Trajectory tracking of unmanned surface vessels based on sliding mode predictive control[J]. Electronics Optics & Control, 2023, 30(9): 92–98 (in Chinese). doi: 10.3969/j.issn.1671-637X.2023.09.016
[15] 郭琳钰, 高剑, 焦慧锋, 等. 基于RBF神经网络的自主水下航行器模型预测路径跟踪控制[J]. 西北工业大学学报, 2023, 41(5): 871–877. doi: 10.1051/jnwpu/20234150871 GUO L Y, GAO J, JIAO H F, et al. Model predictive path following control of underwater vehicle based on RBF neural network[J]. Journal of Northwestern Polytechnical University, 2023, 41(5): 871–877 (in Chinese). doi: 10.1051/jnwpu/20234150871
[16] 李诗杰, 刘泰序, 刘佳仑, 等. 基于MPC-IMFAC的船舶路径跟随控制方法研究[J/OL]. 中国舰船研究, 2024: 1−9 (2024-01-23)[2024-12-20]. https://doi.org/10.19693/j.issn.1673-3185.03629. LI S J, LIU T X, LIU J L, et al. Ship path-following control method based on MPC-IMFAC[J/OL].Chinese Journal of Ship Research, 2024: 1−9(2024-01-23) [2024-12-20]. https://doi.org/10.19693/j.issn.1673-3185.03629 (in Chinese).
[17] TANK D W, HOPFIELD J J. Simple 'neural' optimization networks: an A/D converter, signal decision circuit, and a linear programming circuit[J]. IEEE Transactions on Circuits and Systems, 1986, 33(5): 533–541. doi: 10.1109/TCS.1986.1085953
[18] KENNEDY M P, CHUA L O. Neural networks for nonlinear programming[J]. IEEE Transactions on Circuits and Systems, 1988, 35(5): 554–562. doi: 10.1109/31.1783
[19] XIA Y S, LEUNG H, WANG J. A projection neural network and its application to constrained optimization problems[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002, 49(4): 447–458. doi: 10.1109/81.995659
[20] XIA Y S, WANG J. A bi-projection neural network for solving constrained quadratic optimization problems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(2): 214–224. doi: 10.1109/TNNLS.2015.2500618
[21] 季政, 楼旭阳, 吴炜. 基于神经动态优化的非线性系统近似最优跟踪控制[J]. 控制与决策, 2021, 36(1): 97–104. doi: 10.13195/j.kzyjc.2020.0056 JI Z, LOU X Y, WU W. Approximate optimal tracking control for nonlinear systems based on neurodynamic optimization[J]. Control and Decision, 2021, 36(1): 97–104 (in Chinese). doi: 10.13195/j.kzyjc.2020.0056
[22] SKJETNE R, FOSSEN T I, KOKOTOVIĆ P V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory[J]. Automatica, 2005, 41(2): 289–298. doi: 10.1016/j.automatica.2004.10.006
[23] 陈虹. 模型预测控制[M]. 北京: 科学出版社, 2013: 1−30. CHEN H. Model predictive control[M]. Beijing: Science Press, 2013: 1−30 (in Chinese).
计量
- 文章访问数: 142
- HTML全文浏览量: 39
- PDF下载量: 32
