Study on the residual vertical bending strength of large open-box girders under random pitting corrosion
-
摘要:目的
旨在研究随机点蚀作用下大开口箱型梁的垂向弯曲剩余强度，提出一种基于实测数据的随机点蚀建模方法，并通过非线性有限元分析评估腐蚀对结构极限强度的影响。
方法基于现有研究中的实测船体板点蚀深度数据，引入点蚀深度分布模型，开发相应的数值模型，以评估腐蚀对大开口箱型梁的剩余极限强度的影响。研究中，采用Python在ABAQUS中进行二次开发，实现点蚀深度分布模型的自动化生成和数值模拟分析。通过非线性有限元分析，研究不同腐蚀参数对箱型梁极限强度的影响。
结果结果表明，在相同腐蚀体积损失下，点蚀半径对极限强度的影响较小，最大平均值和最小平均值之间的差异仅为0.89%。随着相对点蚀面积和相对点蚀深度的增加，极限强度折减系数呈线性下降趋势，最小值分别为0.83和0.85。此外，当点蚀深度服从Weibull分布时，中拱工况下箱型梁的极限强度最大下降12.0%，中垂工况下箱型梁的极限强度最大下降16.7%。基于大量数值模拟结果，得到了考虑随机点蚀损失的大开口箱型梁在中拱和中垂两种垂向弯曲作用下的剩余极限强度经验公式。
结论所提方法可为老化船体结构在垂向弯矩作用下的剩余极限强度评估提供重要参考，具有较强的实用性和推广价值。
Abstract:ObjectiveThis paper aims to investigate the residual vertical bending strength of large open-box girders under random pitting corrosion. A stochastic pitting corrosion modeling method based on empirical data is proposed, and the impact of corrosion on the ultimate strength of structures is evaluated through nonlinear finite element analysis.
MethodsTo address this, a depth distribution model of pitting corrosion based on empirical pitting depth data from hull plates is constructed, and a corresponding numerical model is developed to assess the influence on the residual ultimate strength of corroded large-open box girders. In this study, a secondary development in Python within ABAQUS is employed to automate the generation of the pitting depth distribution model and the numerical simulation analysis. Nonlinear finite element analysis is performed to evaluate the influence of various corrosion parameters on the ultimate strength of the box girder.
ResultsThe results indicate that, under the same corrosion volume loss, the effect of pitting radius on ultimate strength is minimal, with a difference of only 0.89% between the maximum and minimum average values. As the relative pitting area and relative pitting depth increase, the ultimate strength reduction factor shows a linear decreasing trend, with minimum values of 0.83 and 0.85, respectively. Additionally, When the pitting depth follows a Weibull distribution, the ultimate strength of the box girder decreases by a maximum of 16.7% under hogging conditions and 12.6% under sagging conditions. Finally, based on extensive numerical simulations, an empirical formula for predicting the residual ultimate strength of large open-box girders under vertical bending loads, considering random pitting loss, is also proposed.
ConclusionsThe methods presented in this paper provide significant references for assessing the residual ultimate strength of aging hull structures under vertical bending moments, demonstrating strong practicality and potential for broader application.
-
0. 引 言
评估船体的垂向弯曲承载能力是评估船体梁极限强度的必要步骤之一[1]。这种极限强度是船体在中垂或中拱状态下发生断裂事故的关键指标，而腐蚀是导致加剧这些事故发生的主要因素之一。2002年，希腊航运公司所属Prestige号油轮发生断裂事故，事故报告显示其船体钢板因长期服役受到严重腐蚀，导致关键部位的强度不足，最终在恶劣海况下失效。因此，根据适用的船级社规则，评估腐蚀严重的大型老龄船舶（如油轮、散货船和集装箱船）的剩余极限强度已成为当务之急。由于实际船舶结构的复杂性，直接研究其极限强度将耗费巨大的计算成本和时间成本，依靠现有技术对实船进行大量参数化研究并不现实。然而，箱型梁模型作为一种简化的船体模型，其设计目的是复制船舶结构在弯矩作用下的屈曲行为，并合理反映实船的极限强度特性和力学性能。通常情况下，箱型梁结构的模型由带有加强筋的板组成，其已被验证为船舶舯部结构的代表模型。
点蚀作为一种腐蚀简化方式在局部船体板结构中已经被广泛应用[2-3]，船体板上点蚀发生的位置分布以及深度的特征得到了学者们的广泛研究[4-6]。与局部船体板结构不同的是，船体梁通常因为其结构本身的复杂性为船体垂向弯曲极限强度的研究带来了较大困难。为了有效提高船体结构的计算效率，并能够反映实际船舶在遭受垂向弯矩作用时的极限状态，Nishihara[7]提出了一种估算船体梁极限弯矩的方法，并在箱型梁模型上成功复制了适用于真实船舶中心部分的条件。在这种简化模型得到有效验证后，学者们通过试验方法和非线性有限元方法对箱型梁在承受弯曲、剪切和扭转载荷时极限强度的变化进行了研究[8-11]，其中崔虎威团队[9]和石贵杰团队[11]分别研究了在静态加载和动态加载工况下初始缺陷对箱型梁极限强度的影响。Saad-Eldeen团队[12]和冯亮团队[13]分别通过实验方法和非线性有限元方法研究了腐蚀损伤下箱型梁的剩余极限强度。
之前的研究表明，仅仅依靠对腐蚀船体结构进行传统的规则点蚀简化，会忽略点蚀在空间上的随机分布对结构强度和稳定性的实际影响[13]。因此，要对腐蚀船体结构进行全面评估，需要采用更复杂的模型或综合分析来考虑随机腐蚀的影响。本文将提出的随机点蚀箱型梁建模方法，通过引入实测数据并结合空间随机分布模型，基于Python有限元软件在ABAQUS中进行二次开发方式实现。通过突破传统方法中对腐蚀效应进行规则分布简化处理的局限，能够更精确地量化点蚀深度和分布位置对船体结构极限强度的影响。在腐蚀模型的生成和非线性有限元分析阶段，通过实现全流程自动化集成，以大幅提升模拟效率。在对大开口箱型梁的剩余极限强度进行参数化分析后，拟合垂向弯矩作用下大开口箱型梁剩余极限强度的预测公式。最后，通过非线性有限元分析与腐蚀概率分布模型的结合，揭示腐蚀空间分布不确定性对结构性能的复杂影响，期望为未来优化模型和扩展应用范围提供新方向。
1. 非线性有限元模型
1.1 基本模型的建立
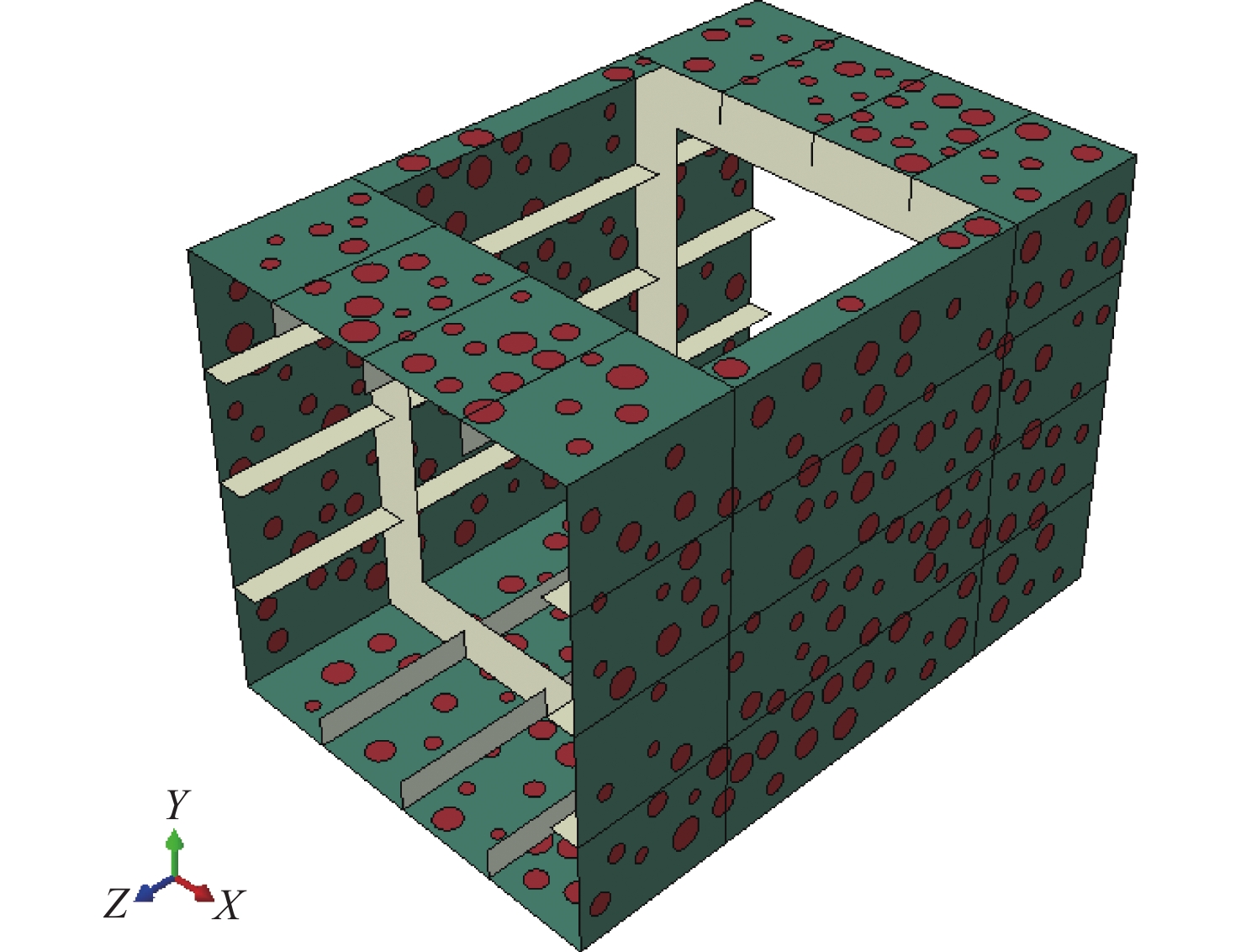
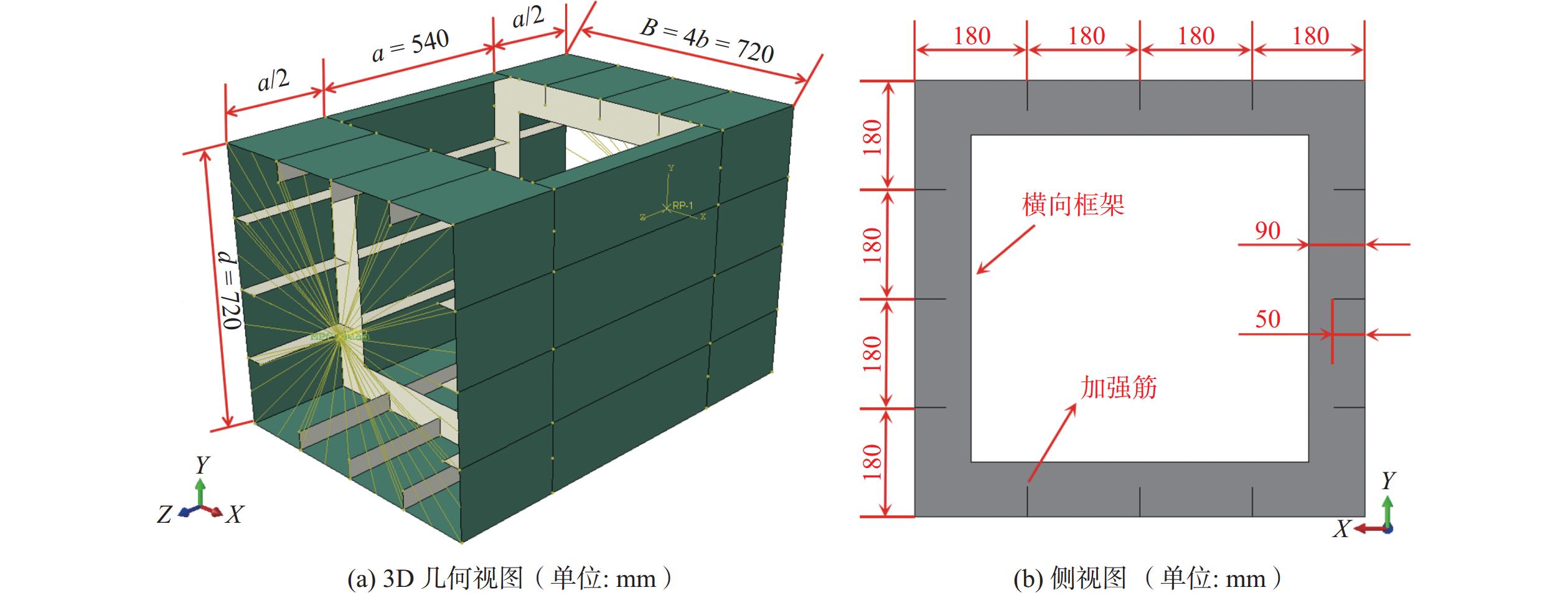
采用的有限元模型源自前言介绍的Nishihara[7]的MST-3箱型梁，并通过在箱型梁中引入一个大开口来实现[13]，具体尺寸如图1所示。为了确保中间部分的梁段在无边界干扰的条件下受力，模型在前后两端各扩展了1/2个舱段，形成了由1/2 + 1 + 1/2舱段组成了本文的大开口箱型梁结构。甲板开口的累计宽度超过了船宽的70%，符合IACS规则对大型甲板开口的规定条件。甲板开口箱型梁的材料特性详见表1。在非循坏加载条件下，通常不需要考虑材料的硬化效应。因此，假定材料是理想的弹性材料，以确保对极限强度的估计更为保守。
![]()
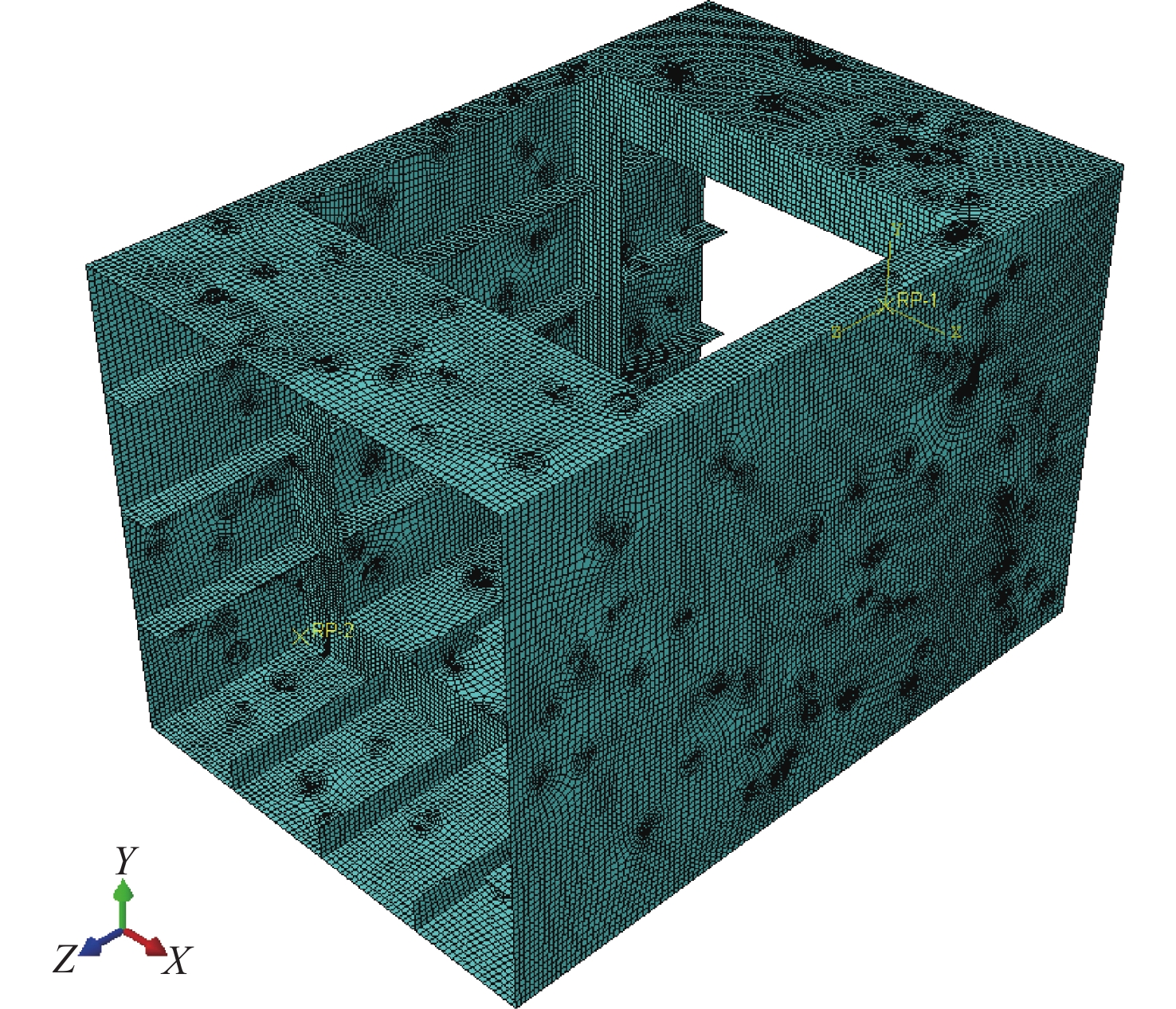
图 1 甲板大开口箱型梁模型示意图Figure 1. Schematic diagram of the box girder model with large deck opening表 1 材料属性Table 1. Material properties参数 数值 弹性模量 E/MPa 2.11×105 泊松比 υ 0.277 屈服强度 σy/MPa 293 采用的边界条件参考Wang等[14]的方法，为将弯矩有效转移到有限元模型中并确保箱型梁在受垂向弯曲载荷作用下前后两端截面保持平面刚性运动，首先使用ABAQUS中的MPC多点约束将箱型梁前后端面与参考点RP-1和RP-2耦合，两个参考点分别定义为中性轴与箱型梁前后两个截面与对称中心线的交点。如图1所示，定义的边界条件和加载条件分别应用于参考点RP-1和RP-2。在参考点RP-1处，其所有6个自由度均受约束；相反，在参考点RP-2（位于箱型梁的前端），其6个自由度均不受约束，而中拱和中垂为两种垂向弯曲方式，并通过施加旋转角度在RP-2上，即Rx = ±1（正负分别对应中拱和中垂两种垂向弯曲方式）。
初始变形是影响梁在承受载荷时失稳行为的重要因素之一。初始变形的半波数会影响梁的整体刚度和变形特性，而幅值较大的初始变形会导致箱型梁更早进入屈曲或失稳状态，进而降低其承载能力。采用了Zhang和Khan[15]的初始变形形状，如式（1）～式（3）所示。初始变形分为两种模式即局部变形和整体变形。
wp=b200cos(mπxa)sin(nπyb)+a1000cos(πxa)sin(πyB) (1) ww=hw200cos(mπxa)sin(nπzhw)+za1000hwcos(πxa) (2) a/b⩽ (3) 式中：wp和ww分别适用于钢板和加强筋；参数a表示一个舱段的长度；参数b和B分别表示加强筋之间的距离和甲板开口箱型梁模型的总宽度；hw是加强筋的高度；m和n分别表示纵向和横向初始变形的半波数。根据经验，n的值通常取为1，对于参数m，当a/b不是整数时，m的值由式（3）确定，并取满足不等式条件的最小值。
为确保所使用的非线性有限元方法的有效性，用本研究未开口的MST-3箱型梁分别与Nishihara[7]的MST-3试验结果和李政杰[16]的MST-3有限元分析结果对比，几种对比结果如下表2。3种模型的极限强度相近，证明本文的非线性有限元方法能够合理反映箱型梁的极限强度。
表 2 与其他学者研究中箱型梁的极限强度对比Table 2. Comparison with the ultimate strength of box girders in other scholars' studies1.2 腐蚀模型的建立
1.2.1 随机点蚀生成方法
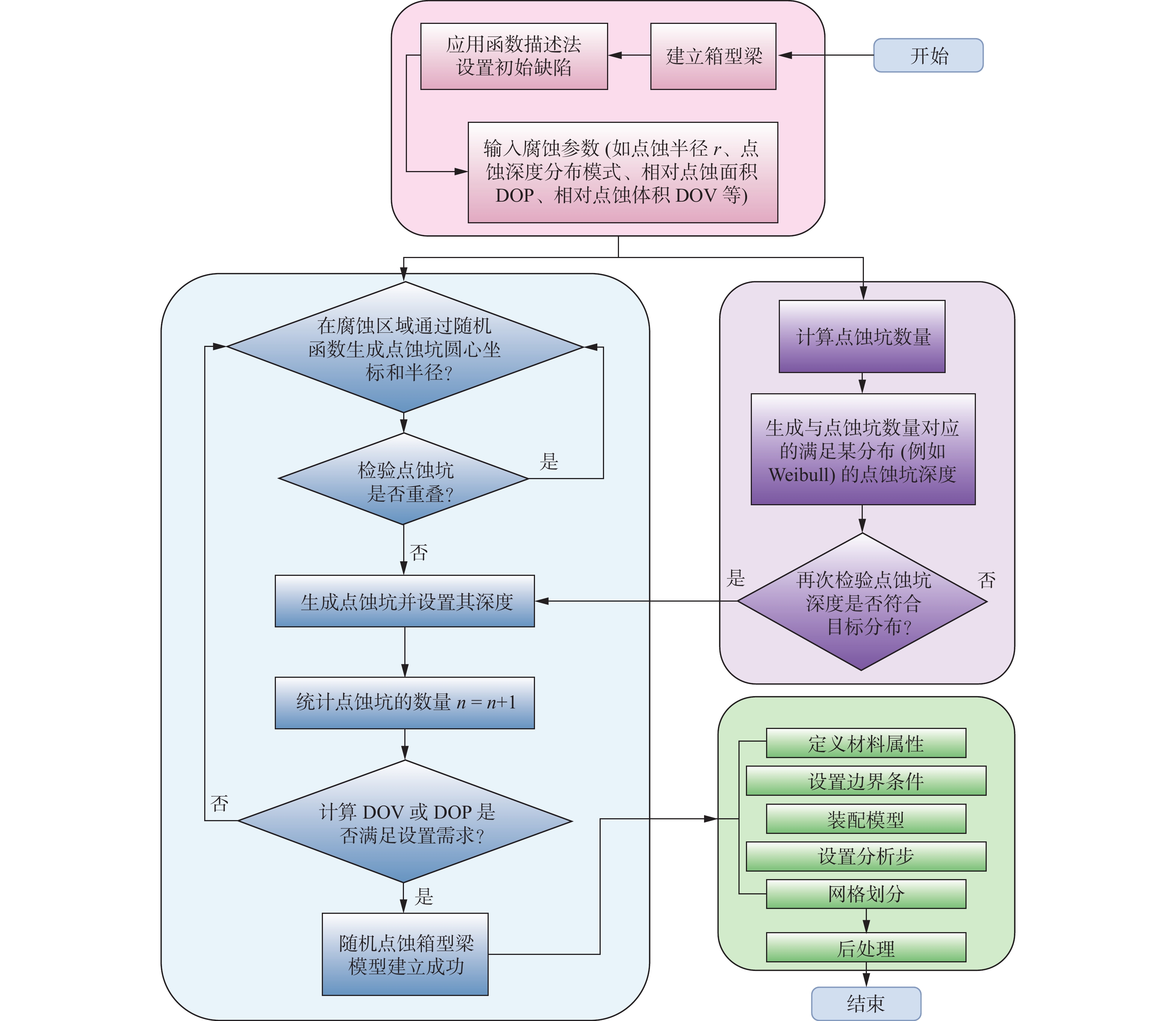
腐蚀表现出多种多样的特征，由于点蚀坑形态的不同对计算结果没有明显影响[17]，因此采用圆形蚀坑作为腐蚀的简化形态。如图2所示，在后续研究中点蚀随机分布在甲板开口箱型梁的甲板、底板和两块侧板上，点蚀的位置、点蚀面积和点蚀深度根据参数化分析需求分别作为不同的常数或变量处理。假定随机点蚀之间没有重叠，这是因为多个重叠的点蚀坑可由一个半径和深度更大的点蚀坑代替[18]。随后，在ABAQUS软件中编写并使用了Python程序来实现随机点蚀并进行有限元计算，具体技术路线见图3。其基本思想是使用随机数在定义区域内生成有限数量的不同半径的圆，并确保任意两个点蚀圆心间的距离大于其半径之和。点蚀信息的生成和处理是这一过程的重要部分，点蚀的一个随机特征是点蚀的分布，由圆心的位置向量M表示。点蚀的另一个随机特征是点蚀的形状，由半径r和相对点蚀深度tr/t组成，形成向量P。点蚀深度根据分析需求，可采用均匀常数的规则深度或随机生成的点蚀深度，例如下式中点蚀深度分布满足基于Paik和Kim[19]对实际点蚀船体板统计的Weibull分布。
f\left( x \right) = \frac{\alpha }{\beta }{\left( {\frac{{x - \gamma }}{\beta }} \right)^{\alpha - 1}} \cdot \exp \left[ { - {{\left( {\frac{{x - \gamma }}{\beta }} \right)}^\alpha }} \right] (4) \left\{ \begin{gathered} \alpha = 0.0020Y_{\text{e}}^3 - 0.0994Y_{\text{e}}^2 + 1.5604{Y_{\text{e}}} - 6.0025 \\ \beta = 0.0004Y_{\text{e}}^3 - 0.0248Y_{\text{e}}^2 + 0.4793{Y_{\text{e}}} - 2.3812 \\ \end{gathered} \right. (5) 式中：f （x）是腐蚀深度（点蚀深度）的函数；Ye是船体板的服役时长（年）；α是形状参数；β是尺度参数；γ是位置参数，γ在Paik和Kim[19]的研究中设为0。
1.2.2 单元类型及网格收敛性分析
网格采用ABAQUS软件的S4R单元类型，通常用于模拟薄壳结构的应力、应变和变形等行为。腐蚀通常会导致局部变形和应力集中，点蚀箱型梁模型则需要更精细的网格来准确捕捉这些效应。因此，本研究在图4所示的完整区域建立了适当大小的网格，并在腐蚀区域采用了更密集的网格，以提高结果的精准度。此外，为确保网格细化后结果趋于稳定，采用了粗糙、中等、精细3种密度进行网格划分。表3比较了不同网格尺寸的点蚀大开口箱型梁在中拱工况下的极限抗弯强度的相对误差，可以发现3种方案之间的误差不到1%，为了在计算效率和精度之间取得平衡，后续研究选择了中等尺寸的网格尺度。
表 3 网格收敛性分析Table 3. Mesh convergence analysis网格尺寸 极限弯矩/kN∙m 相对误差 网格数量/个 精细 403.34 — 138482 中等 403.27 0.017% 59439 粗糙 403.93 0.149% 38097 2. 结果与讨论
2.1 腐蚀参数对极限强度的影响
2.1.1 点蚀半径的影响
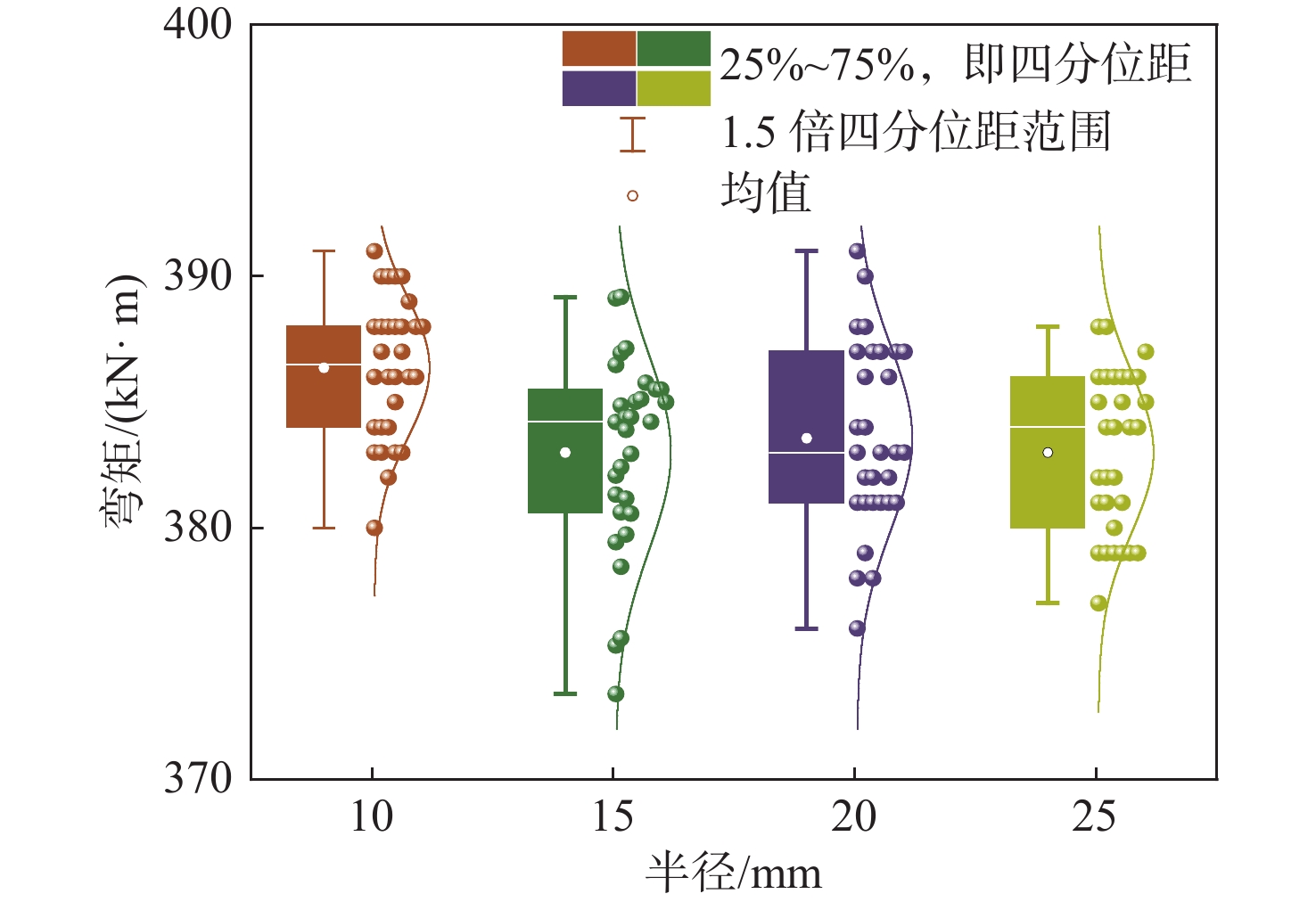
为比较不同点蚀半径对箱型梁极限强度的影响行为，比较了点蚀半径分别为10，15，20和25 mm在箱型梁中拱作用下的极限弯矩，每组参数取30个模型。数据分析采用了图5展示的箱线图，由图可以发现每组模型的极限弯矩集中在380～390 kN∙m范围内。此外，将具体数据的极限强度分布与正态分布曲线进行对比后发现，极限弯矩的分布情况与正态分布接近。在比较4组极限强度数据的平均值后，最大平均值和最小平均值分别为386.38和383 kN∙m，相对误差为0.89%。这表明，腐蚀体积和腐蚀深度相同下，不同凹坑半径对极限强度的影响很小。
![]()
图 5 不同点蚀半径下的极限强度箱线图Figure 5. Box-plot of ultimate strength at different radii of pitting corrosion2.1.2 相对点蚀面积的影响
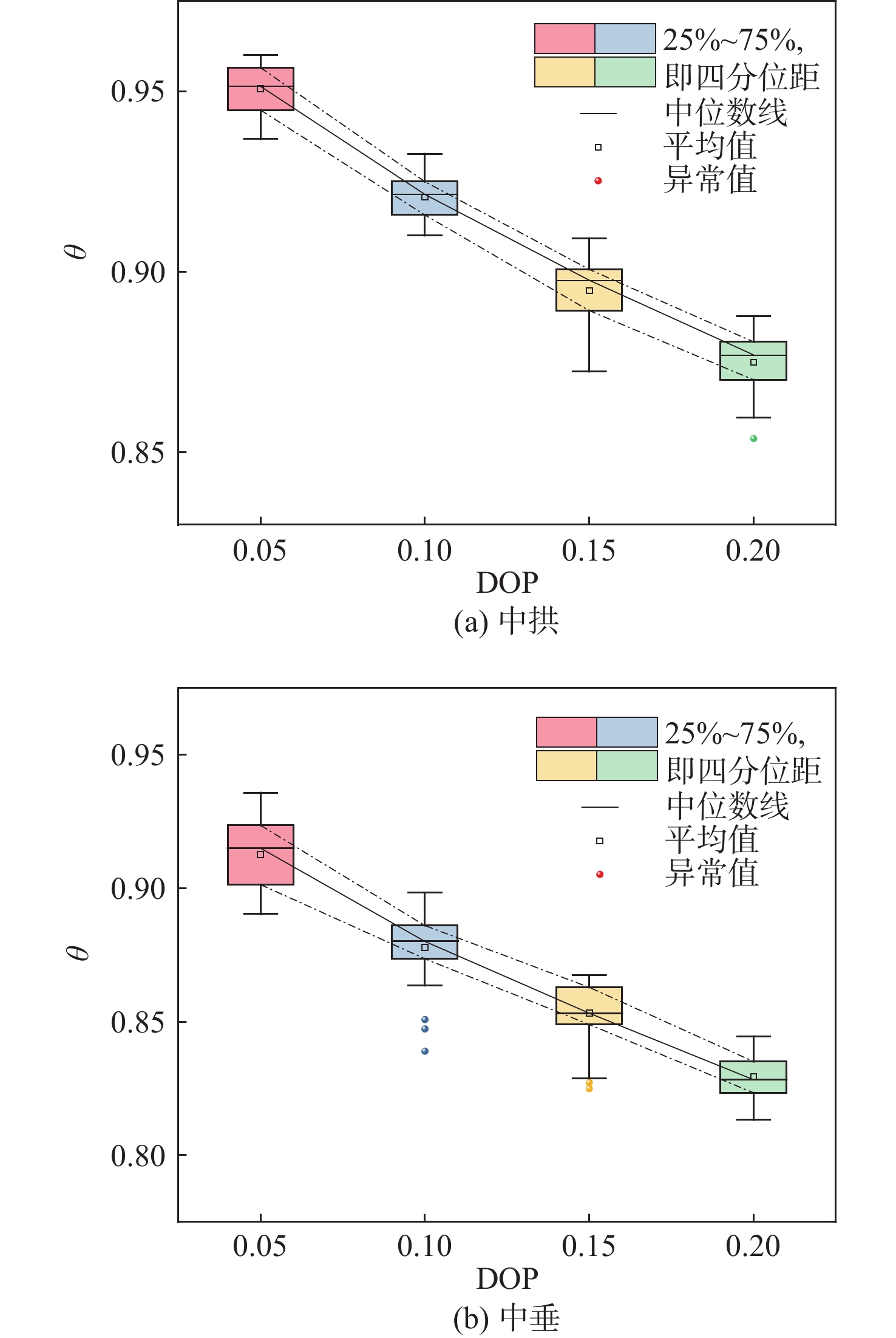
相对点蚀面积（点蚀面积与箱型梁表面积的比值）是衡量点蚀对船体结构极限强度影响的一个重要指标，本小节总计进行了120次随机模拟，以研究每组相对点蚀面积下极限强度的变化规律。考虑到船级社规则的范围[6]，引入计算模型的相对点蚀面积（DOP）限制在25%以下，相对点蚀深度tr/t （点蚀深度与箱型梁板格厚度的比值）保持恒定为0.333，每组进行30次重复随机模拟并计算箱型梁的极限强度。此外，由于大开口的影响，分别分析了中拱和中垂两种工况下箱型梁的极限强度性能。为了更直观的了解随机点蚀对箱型梁极限强度的影响行为，使用极限强度折减系数θ来量化点蚀对结构强度的削弱效应，其中θ是点蚀箱型梁的极限弯矩与未腐蚀箱型梁的极限弯矩之比。
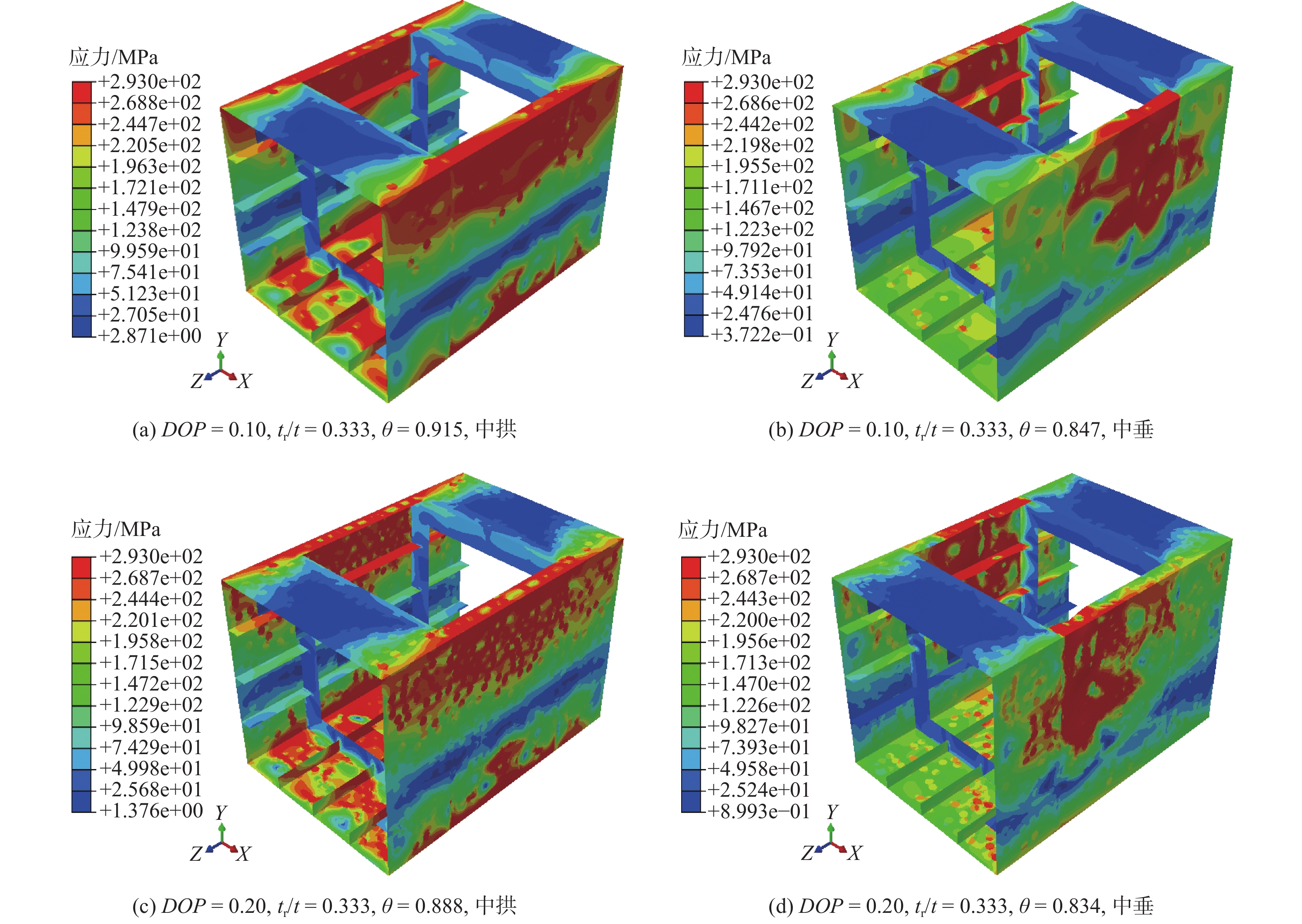
图6（a）和图6（b）分别展示了中拱和中垂作用下不同DOP的极限弯矩。在4组箱线图的上四分位数、中位数和下四分位数相连后，可以发现当DOP线性下降时，中拱状态下θ的平均值由0.95呈线性下降趋势至0.87；中垂状态下θ的平均值由0.91呈线性下降趋势至0.83。值得关注的是，尽管DOP和极限强度的平均值之间存在负相关关系，在例如中垂工况下，DOP = 0.10组中出现了多个低于DOP = 0.15组极限强度平均值的异常点，因此，在不考虑点蚀空间分布的随机性的情形下，指定的规则点蚀分布可能会导致较高的结构安全风险。图7展示了不同DOP下箱型梁的等效应力分布情况。可以观察到一个明显的趋势：随着DOP由0.10增加至0.20，侧板和底板的局部应力集中现象更加显著，从而导致中拱和中垂工况下极限强度折减系数θ由0.915和0.847分别降低至0.888和0.834。此外，在中垂状态下，由于图7（d）中侧板的点蚀加剧，并且主要集中在左侧，这直接导致箱型梁的整体失效区域相较于图7（b）整体向左侧移动，这说明点蚀的分布不均会造成箱型梁的失效模式随之转变。
![]()
图 6 不同DOP下极限强度折减系数θ的箱线图以及3类分位数线连接图Figure 6. Box plots of ultimate strength reduction factor θ at different DOPs with lines connecting three types of quantiles2.1.3 相对点蚀深度的影响
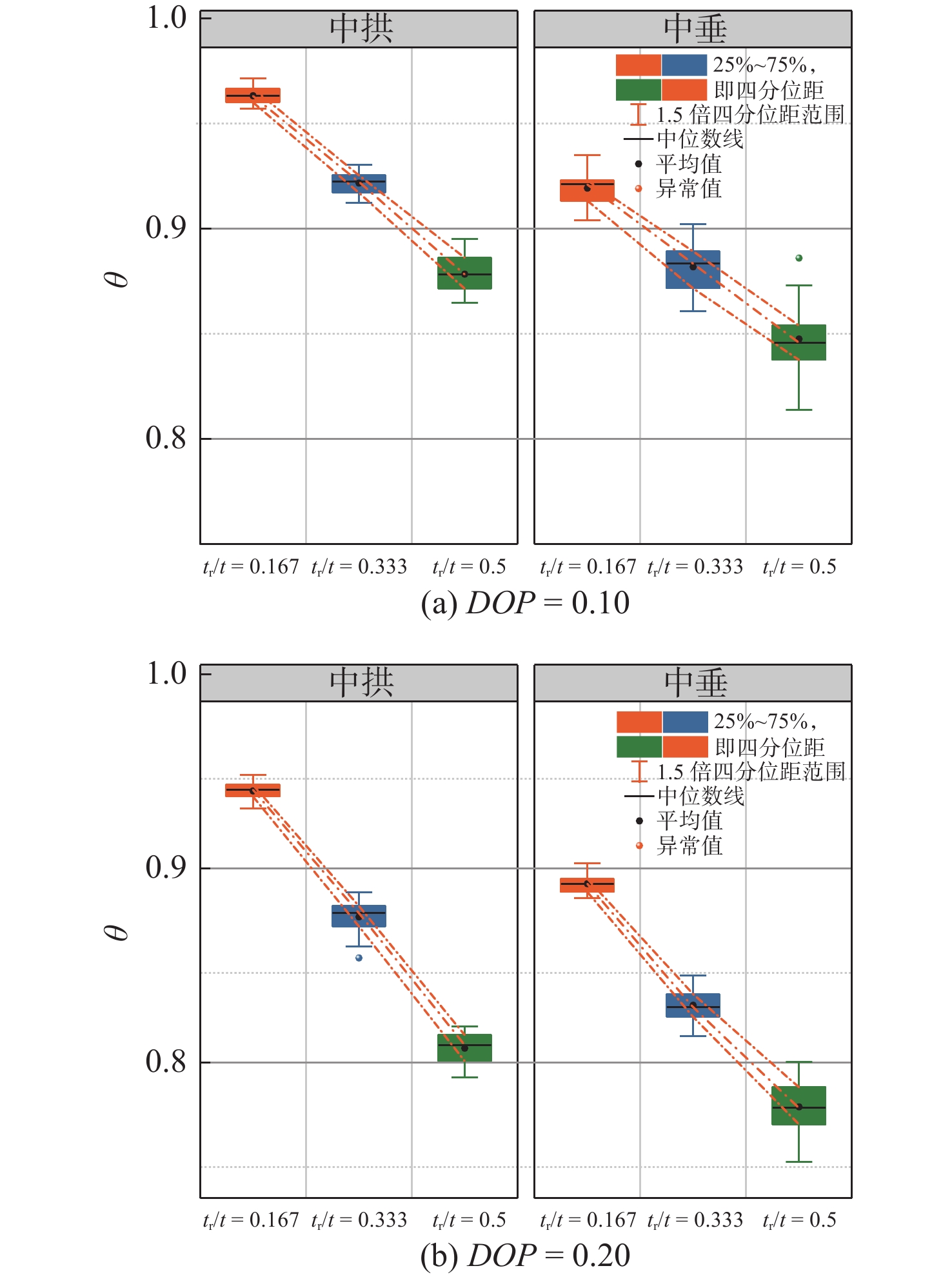
为了深入分析点蚀随机分布下相对点蚀深度（tr/t）对箱型梁极限强度的影响，在分析中，除点蚀深度外，其余参数被固定为常数，具体为r = 20 mm，DOP分别为0.10和0.20，相对点蚀深度分别为0.167，0.333和0.5。每组工况分别在中拱和中垂两种载荷施加方式下重复模拟30次，在计算总计360组模型后，得到图8所示的箱线图。
![]()
图 8 不同相对点蚀深度tr/t下极限强度折减系数θ的箱线图以及三类分位数线连接图Figure 8. Box plots of ultimate strength reduction factor θ at different relative pitting depths tr/t with lines connecting three types of quantiles如图8所示，随着相对点蚀深度值的增大，各组极限强度的分布变得更加离散，例如DOP = 0.10的中垂工况下，θ的波动大小由0.03增至0.07，这是因为相对点蚀深度值的增大会进一步导致腐蚀坑局部区域刚度的下降，腐蚀坑边缘的应力分布发生急剧变化，这种现象进一步降低了腐蚀区域的最小横截面积，导致腐蚀区域更容易发生应力集中。此外，尽管每组数据的波动情况不同，在分别整理了不同组数据的上四分位数、中位数和下四分位数后，发现在中拱工况和中垂工况，极限强度数据的３个分位数都随着点蚀深度的增加而持续线性减小，其中，中拱和中垂下的极限强度均值分别下降至0.88和0.85。
2.1.4 相对点蚀体积的影响
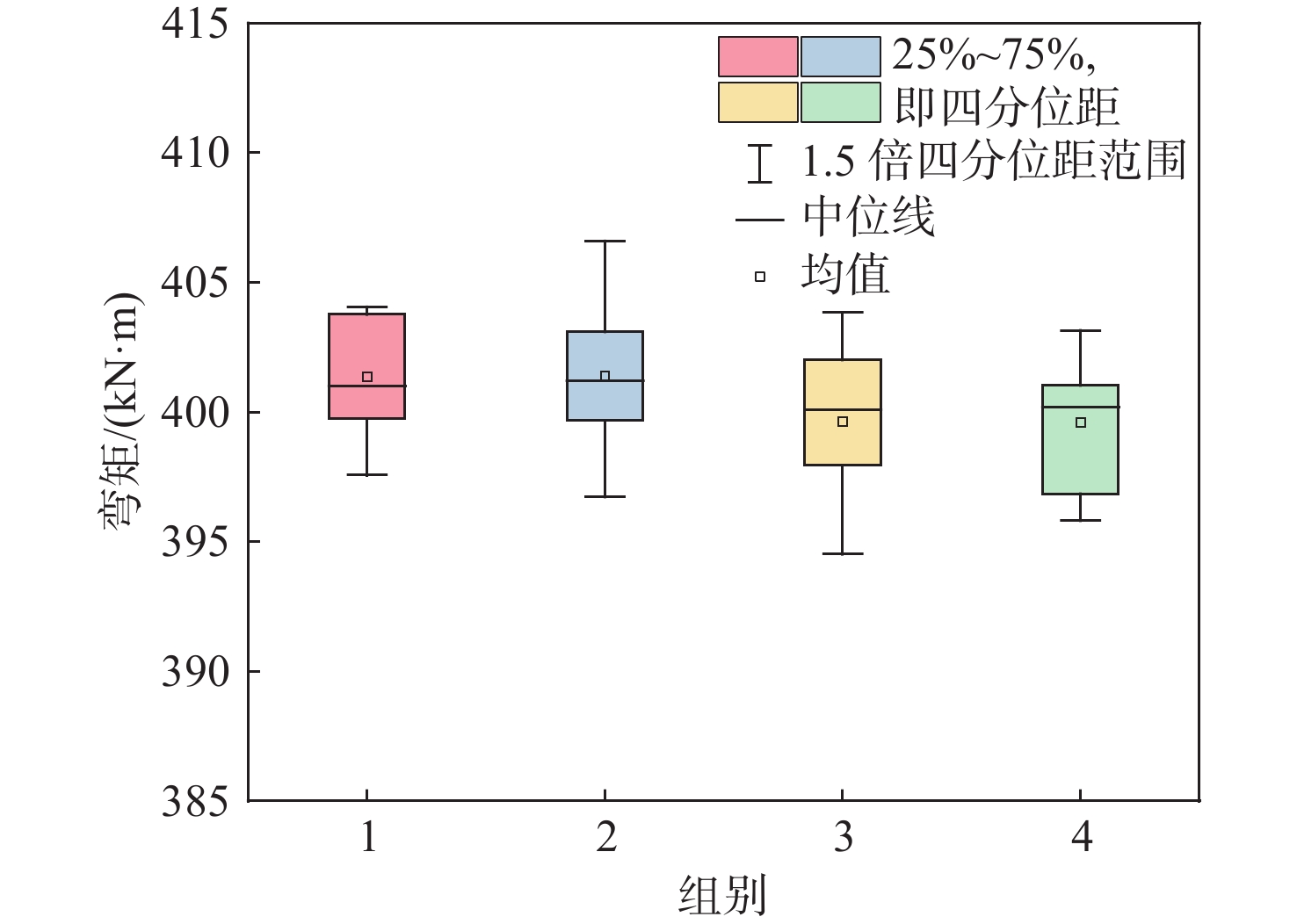
相对点蚀体积（DOV）通常是通过相对点蚀面积（DOP）和平均相对点蚀深度（tr/t）的乘积得出的。在实际情况下，点蚀深度会在整个船壳板上呈现不规则分布。这意味着，如果需要进一步评估实际船体梁的承载能力，点蚀深度随机变化下获得的极限强度应较规则深度分布下更接近实际情况。因此，在明确相对腐蚀面积和相对腐蚀深度对箱型梁极限强度的影响后，在本节中，相对点蚀体积被视为变量，点蚀深度的分布模式来自Paik和Kim[19]的Weibull分布。表4展示了所引入的Paik和Kim[19]的Weibull分布形状参数和比例参数。对每组点蚀深度服从双参数Weibull分布的点蚀大开口箱型梁进行了10组重复随机模拟。在点蚀体积相等的条件下，不同形状和比例参数的4组箱型梁的中拱极限弯矩平均值的最大值和最小值相差0.45%，如图9所示。这种差异化参数特征反映了多种点蚀深度分布模式的存在，然而，这种点蚀深度分布的差异导致箱型梁在腐蚀量相同的情况下极限强度相似。进一步的分析表明，当考虑到点蚀深度遵循Weibull分布时，形状和尺度参数的变化对箱型梁极限强度的影响可以忽略不计。
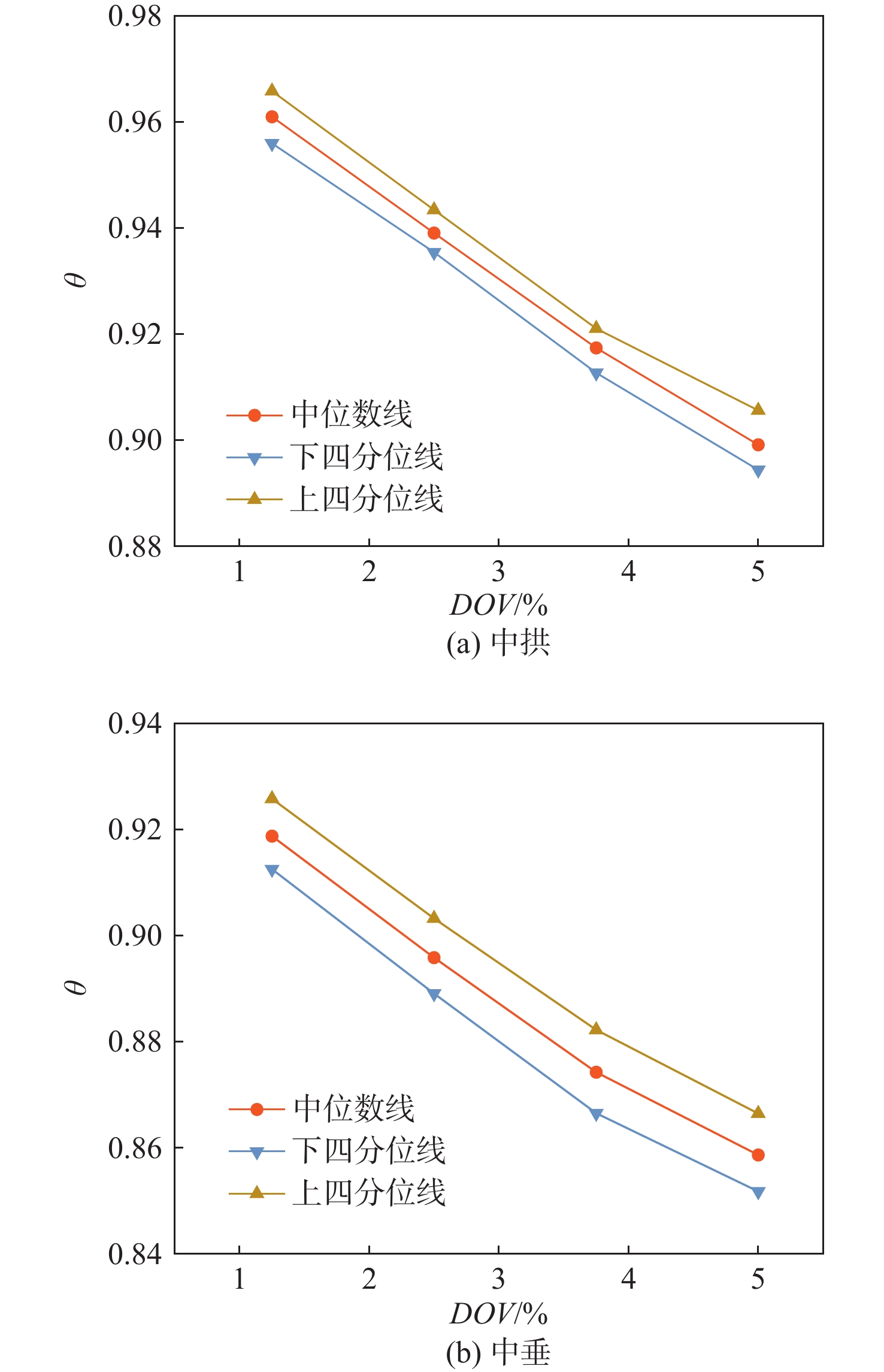
表 4 各组Weibull分布的形状参数和位置参数Table 4. Shape and scale parameters of the Weibull distribution for each group组别 形状参数 尺度参数 1 1.269 0 0.800 6 2 1.652 8 0.706 8 3 1.922 0 0.398 7 4 2.278 6 0.999 1 ![]()
图 9 不同形状和尺度参数的极限强度箱线图Figure 9. Box-plots of ultimate strength for different shape and scale parameters此外，为进一步研究大开口箱型梁在不同相对点蚀体积下的极限强度分布规律，研究中考虑了4组相对点蚀体积（DOV），分别为1.25%，2.5%，3.75%和5%。每组分别进行50次随机数值模拟，最终分别得到中拱和中垂工况下箱型梁的极限强度数据。在相对点蚀体积最大值为5%的中拱工况下，折减系数θ在0.880至0.918之间波动；在中垂工况下，折减系数θ在0.833至0.874之间波动，即当点蚀深度服从Weibull分布时，中拱工况下箱型梁的极限强度最大下降了12.0% ，中垂工况下箱型梁的极限强度最大下降了16.7%。图10所示为不同点蚀体积下每组箱型梁极限强度的上四分位数、中位数和下四分位数的分布图。与相对点蚀体积和相对点蚀深度规律一致的是，随着相对点蚀体积的增加，箱型梁的极限承载力呈现出随之线性减小的规律。
![]()
图 10 极限强度折减系数θ的分位数变化曲线Figure 10. Interquartile variation curves of ultimate strength reduction factor θ2.2 极限强度概率分布
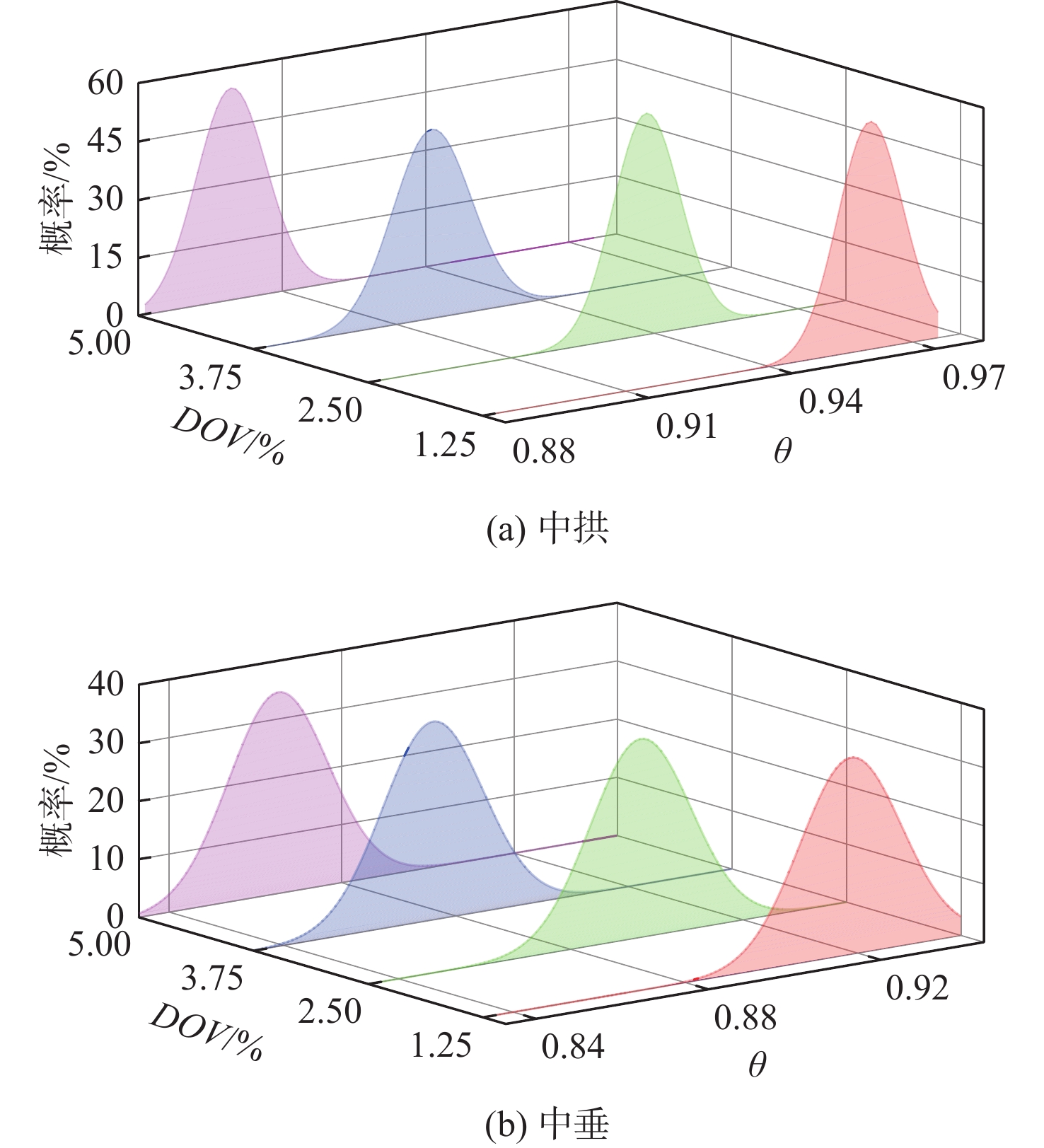
为了更全面地评估结构的可靠性，对同一腐蚀体积下的箱型梁进行50次随机模拟可以得到不同腐蚀形态下的极限强度分布，进而掌握腐蚀对结构极限强度的总体影响范围，为设计安全裕度提供依据。图11所示为极限强度的三维概率分布图。可见，无论是在中拱还是中垂工况下，不同相对点蚀体积损失下甲板大开口箱型梁的极限弯矩均近似于正态分布的特征。
![]()
图 11 不同DOV下极限强度概率分布图Figure 11. Probability distribution of ultimate strength under different DOVs为进一步验证极限强度分布是否符合正态分布规律，对结果进行Kolmogorov−Smirnov正态性检验，显著性水平设定为 0.05。检验分别针对不同相对腐蚀量下的极限强度数据展开。通过计算得到的统计量和对应的p 值，对原假设（数据服从正态分布）进行了推断。检验结果如表5所示，其中 p 值均大于显著性水平（0.05）。因此，在此显著性水平下，可以接受数据符合正态分布的假设。这表明，尽管存在不同的相对腐蚀量，大开口箱型梁的整体纵向极限弯矩仍呈现出正态分布的特征。
表 5 Kolmogorov−Smirnov 正态性检验结果Table 5. Results of the Kolmogorov−Smirnov test加载方式 DOV/% Kolmogorov−Smirnov 统计量 P值 中拱 1.25 0.047 37 1 2.50 0.115 38 0.490 1 3.75 0.094 98 0.7633 15 0.057 81 1 中垂 1.25 0.077 89 1 2.5 0.074 53 1 3.75 0.073 04 1 5 0.090 88 0.826 0 2.3 极限强度经验公式拟合
经过前面的讨论，发现随机点蚀对箱型梁极限承载能力的影响至关重要。此外，基于Weibull分布的点蚀深度无疑比基于规则简化的点蚀深度更贴近实际情况。为了评估大开口老化船舶的安全性，本文以数值计算结果为基础，提出了一个经验公式，用于预测箱型梁在中拱和中垂弯曲荷载下随机点蚀对极限强度的影响行为。考虑到相对点蚀面积和相对点蚀深度的耦合影响，箱型梁极限强度的预测取决于作为主要参数的相对点蚀体积（DOV）。随后根据每个数据集的中位数进行线性拟合，并加入误差项R （−0.005≤ R ≤ 0.005），以适应点蚀随机效应下极限强度的上下波动，得出以下公式。
\theta =1-0.025\times DOV\pm R(中拱\text{)} (6) \theta =1-0.035\times DOV\pm R(中垂\text{)} (7) 与式（8）、式（9）由Hong等[20]拟合的受规则点蚀作用下大开口箱型梁的极限强度经验公式不同，本研究拟合的公式考虑了点蚀位置和点蚀深度的随机分布。因此，将两组公式进行对比可以发现，将点蚀进行规则分布的简化往往会低估腐蚀对结构极限强度的削弱作用。
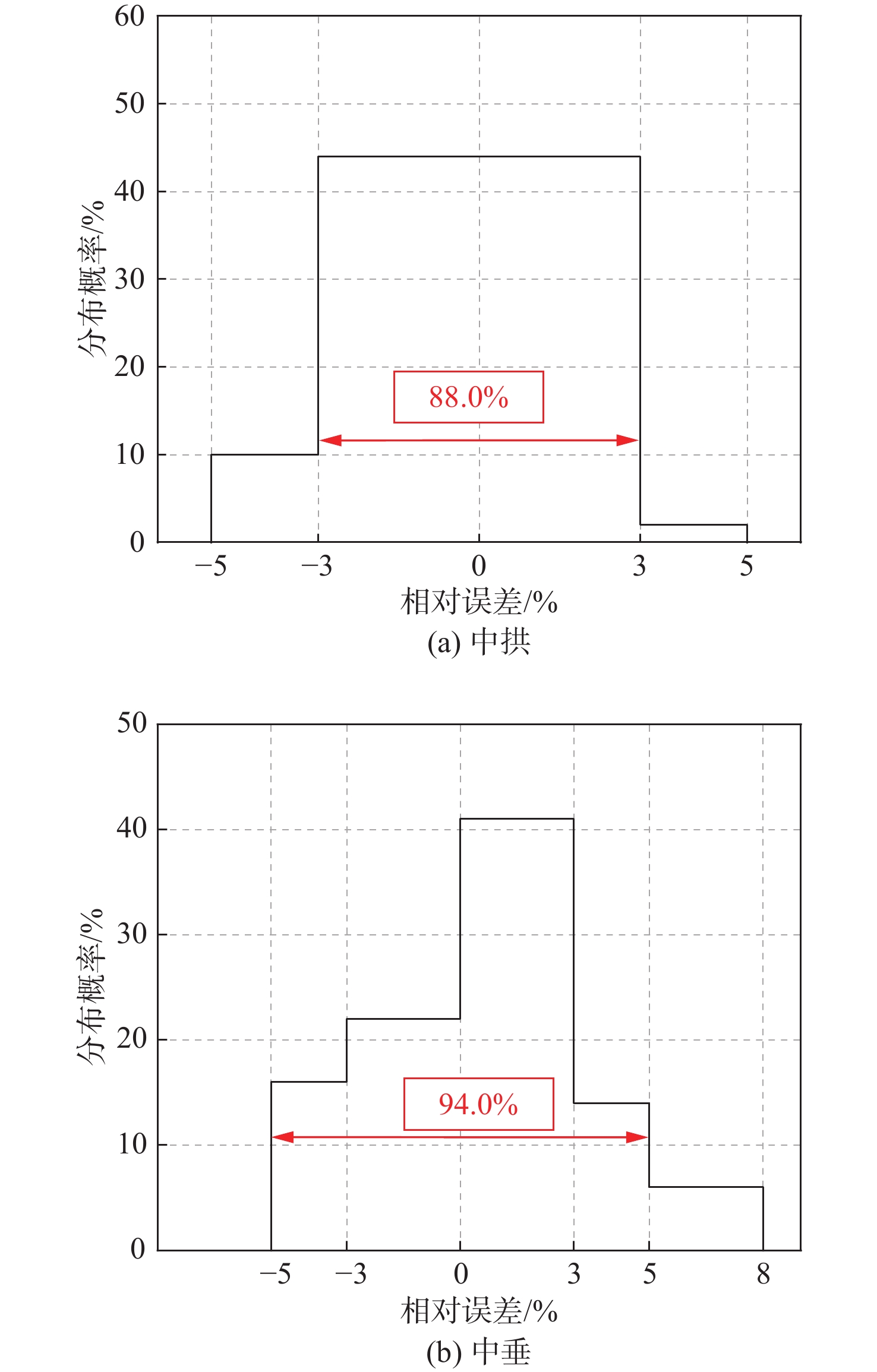
\theta =1-0.02\times DOV(中拱\text{)} (8) \theta =1-0.0254\times DOV(中垂\text{)} (9) 为了验证公式是否出现过度拟合，分别取DOV为1%，2%，3%，4%和5%的５组数据来验证公式。从每组数据中随机生成10个腐蚀箱型梁模型，并分别计算中拱和中垂两种加载模式的极限弯矩。如图12所示的结果表明，中拱加载方式下的有限元结果与公式计算结果的相对误差均在5%以内；中垂加载方式下有94%的有限元结果与公式计算结果的相对误差在5%以内，这表明公式能够拟合不同点蚀体积的大开口箱型梁的极限强度。公式的参数化能够涵盖不同的数值，并且在新数据的验证下仍然合理。这意味着该经验公式具有较强的通用性，可在不同情况下提供合理的预测。
![]()
图 12 经验公式与有限元结果极限强度误差分布Figure 12. Distribution of error in ultimate strength between empirical formulae and finite element results3. 结 论
本研究提出了一种基于实测数据的随机点蚀建模方法，结合在ABAQUS中进行二次开发实现了腐蚀模型的自动化生成和数值模拟分析。在考虑点蚀随机性的基础上，研究了不同腐蚀参数对船体结构剩余极限强度的影响，将复杂的有限元分析结果归纳为简便的经验公式，以便快速预测不同腐蚀条件下的结构极限强度折减情况。研究结果表明，腐蚀空间分布的不确定性对结构性能有显著影响，所提方法为老化船体结构在垂向弯矩作用下的剩余极限强度评估提供了重要参考。在对大量数值模拟结果进行总结后，得出以下主要结论：
1） 在中拱和中垂两种垂向弯矩作用下，点蚀半径对大开口箱型梁的极限强度几乎没有影响，箱型梁的剩余极限强度一般随相对点蚀面积、相对点蚀深度和相对点蚀体积的增加而减小。值得注意的是，在点蚀集中发生在最危险截面的情况下，箱型梁的极限承载能力会出现更为剧烈的下降。
2） 在点蚀深度服从Weibull分布的条件下，对随机点蚀的箱型梁进行了大量的数值模拟。经过Kolmogorov−Smirnov正态性检验，不同相对点蚀体积损失下的大开口箱型梁在中拱和中垂两种情况下的极限强度分布情况仍符合正态分布规律。
3） 基于大量数值模拟统计结果，给出了考虑随机点蚀损失的大开口箱型梁在中拱和中垂两种垂向弯曲作用下的剩余极限强度经验公式。
在未来研究中，可进一步优化腐蚀船体结构的有限元模型，考虑更多更加贴合实际腐蚀船体结构形貌的数值模拟方法，例如非均匀腐蚀和点蚀相融合的方式，并结合机器学习等先进技术提高评估准度，推动船体结构腐蚀评估的自动化与智能化发展。
-
![]()
图 1 甲板大开口箱型梁模型示意图
Figure 1. Schematic diagram of the box girder model with large deck opening
![]()
图 5 不同点蚀半径下的极限强度箱线图
Figure 5. Box-plot of ultimate strength at different radii of pitting corrosion
![]()
图 6 不同DOP下极限强度折减系数θ的箱线图以及3类分位数线连接图
Figure 6. Box plots of ultimate strength reduction factor θ at different DOPs with lines connecting three types of quantiles
![]()
图 8 不同相对点蚀深度tr/t下极限强度折减系数θ的箱线图以及三类分位数线连接图
Figure 8. Box plots of ultimate strength reduction factor θ at different relative pitting depths tr/t with lines connecting three types of quantiles
![]()
图 9 不同形状和尺度参数的极限强度箱线图
Figure 9. Box-plots of ultimate strength for different shape and scale parameters
![]()
图 10 极限强度折减系数θ的分位数变化曲线
Figure 10. Interquartile variation curves of ultimate strength reduction factor θ
![]()
图 11 不同DOV下极限强度概率分布图
Figure 11. Probability distribution of ultimate strength under different DOVs
![]()
图 12 经验公式与有限元结果极限强度误差分布
Figure 12. Distribution of error in ultimate strength between empirical formulae and finite element results
表 2 与其他学者研究中箱型梁的极限强度对比
Table 2 Comparison with the ultimate strength of box girders in other scholars' studies
下载: 导出CSV
表 3 网格收敛性分析
Table 3 Mesh convergence analysis
网格尺寸 极限弯矩/kN∙m 相对误差 网格数量/个 精细 403.34 — 138482 中等 403.27 0.017% 59439 粗糙 403.93 0.149% 38097
下载: 导出CSV
表 4 各组Weibull分布的形状参数和位置参数
Table 4 Shape and scale parameters of the Weibull distribution for each group
组别 形状参数 尺度参数 1 1.269 0 0.800 6 2 1.652 8 0.706 8 3 1.922 0 0.398 7 4 2.278 6 0.999 1
下载: 导出CSV
表 5 Kolmogorov−Smirnov 正态性检验结果
Table 5 Results of the Kolmogorov−Smirnov test
加载方式 DOV/% Kolmogorov−Smirnov 统计量 P值 中拱 1.25 0.047 37 1 2.50 0.115 38 0.490 1 3.75 0.094 98 0.7633 15 0.057 81 1 中垂 1.25 0.077 89 1 2.5 0.074 53 1 3.75 0.073 04 1 5 0.090 88 0.826 0
下载: 导出CSV
-
[1] 傅伟程, 刘中全, 孔祥韶, 等. 纯弯载荷下箱型梁的非线性相似特性研究[J]. 中国舰船研究, 2023, 18(3): 173–185. doi: 10.19693/j.issn.1673-3185.02551 FU W C, LIU Z Q, KONG X S, et al. Study of similarity characteristic for the buckling process of box girders subjected to bending load[J]. Chinese Journal of Ship Research, 2023, 18(3): 173–185 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.02551
[2] PAIK J K, LEE J M, KO M J. Ultimate shear strength of plate elements with pit corrosion wastage[J]. Thin-Walled Structures, 2004, 42(8): 1161–1176. doi: 10.1016/j.tws.2004.03.024
[3] NAKAI T, MATSUSHITA H, YAMAMOTO N. Effect of pitting corrosion on the ultimate strength of steel plates subjected to in-plane compression and bending[J]. Journal of Marine Science and Technology, 2006, 11(1): 52–64. doi: 10.1007/s00773-005-0203-4
[4] YAMAMOTO N, IKEGAMI K. A study on the degradation of coating and corrosion of ship’s hull based on the probabilistic approach[J]. Journal of Offshore Mechanics and Arctic Engineering, 1998, 120(3): 121–128. doi: 10.1115/1.2829532
[5] TEIXEIRA Â P, SOARES C G. Ultimate strength of plates with random fields of corrosion[J]. Structure and Infrastructure Engineering, 2008, 4(5): 363–370. doi: 10.1080/15732470701270066
[6] WANG R H, SHENOI R A, SOBEY A. Ultimate strength assessment of plated steel structures with random pitting corrosion damage[J]. Journal of Constructional Steel Research, 2018, 143: 331–342. doi: 10.1016/j.jcsr.2018.01.014
[7] NISHIHARA S. Analysis of ultimate strength of stiffened rectangular plate (4th report)[J]. Journal of the Society of Naval Architects of Japan, 1983, 1983(154): 367–375. doi: 10.2534/jjasnaoe1968.1983.154_367
[8] KIM K, YOO C H. Ultimate strengths of steel rectangular box beams subjected to combined action of bending and torsion[J]. Engineering Structures, 2008, 30(6): 1677–1687. doi: 10.1016/j.engstruct.2007.11.011
[9] 崔虎威, 胡润文, 丁启印. 循环弯矩下考虑完整初始缺陷的箱型梁极限强度研究[J]. 中国舰船研究, 2024, 19(2): 120–127. doi: 10.19693/j.issn.1673-3185.03171 CUI H W, HU R W, DING Q Y. Study on ultimate strength of box girder considering intact initialimperfections under cyclic bending moments[J]. Chinese Journal of Ship Research, 2024, 19(2): 120–127 (in Chinese). doi: 10.19693/j.issn.1673-3185.03171
[10] DENG H, YUAN T, GAN J, et al. Experimental and numerical investigations on the collapse behaviour of box type hull girder subjected to cyclic ultimate bending moment[J]. Thin-Walled Structures, 2022, 175: 109204. doi: 10.1016/j.tws.2022.109204
[11] SHI G J, WANG D Y, WANG F H, et al. Analysis of dynamic response and ultimate strength for box girder under bending moment[J]. Journal of Marine Science and Engineering, 2023, 11(2): 373. doi: 10.3390/jmse11020373
[12] SAAD-ELDEEN S, GARBATOV Y, SOARES C G. Experimental assessment of the ultimate strength of a box girder subjected to severe corrosion[J]. Marine Structures, 2011, 24(4): 338–357. doi: 10.1016/j.marstruc.2011.05.002
[13] FENG L, HONG K, LI D Y, et al. Ultimate torsional strength assessment of large deck opening stiffened box girder subjected to pitting corrosion[J]. Ocean Engineering, 2022, 251: 111059. doi: 10.1016/j.oceaneng.2022.111059
[14] WANG C L, WU J M, WANG D Y. Design similar scale model of a 10, 000 TEU container ship through combined ultimate longitudinal bending and torsion analysis[J]. Applied Ocean Research, 2019, 88: 1–14. doi: 10.1016/j.apor.2019.03.016
[15] ZHANG S M, KHAN I. Buckling and ultimate capability of plates and stiffened panels in axial compression[J]. Marine Structures, 2009, 22(4): 791–808. doi: 10.1016/j.marstruc.2009.09.001
[16] 李政杰, 赵南, 司海龙, 等. 基于显式算法的船体梁极限强度非线性有限元分析[J]. 舰船科学技术, 2015, 37(10): 11–15. doi: 10.3404/j.issn.1672-7649.2015.10.003 LI Z J, ZHAO N, SI H L, et al. The nonlinear finite element analysis of ship hull girder's ultimate strength by explicit algorithm[J]. Ship Science and Technology, 2015, 37(10): 11–15 (in Chinese). doi: 10.3404/j.issn.1672-7649.2015.10.003
[17] ZHANG Y, HUANG Y, ZHANG Q, et al. Ultimate strength of hull structural plate with pitting corrosion damnification under combined loading[J]. Ocean Engineering, 2016, 116: 273–285. doi: 10.1016/j.oceaneng.2016.02.039
[18] WANG R H, LIN S Y, DOU P L. Statistical constitutive model of steel in randomly pitted structures[J]. Ocean Engineering, 2022, 243: 110211. doi: 10.1016/j.oceaneng.2021.110211
[19] PAIK J K, KIM D K. Advanced method for the development of an empirical model to predict time-dependent corrosion wastage[J]. Corrosion Science, 2012, 63: 51–58. doi: 10.1016/j.corsci.2012.05.015
[20] HONG K, FENG L, LIU C, et al. Residual ultimate strength of large opening box girder with pitting corrosion damage under torsion and bending loads[J]. Ships and Offshore Structures, 2023, 18(11): 1559–1581. doi: 10.1080/17445302.2022.2129914
计量
- 文章访问数: 47
- HTML全文浏览量: 7
- PDF下载量: 1
