Fault diagnosis of ship diesel power distribution system based on WOA-RF algorithm
-
摘要:目的
船舶柴发配电系统对航行稳定性至关重要，海洋工作环境的严苛性致使其故障频发，为此提出一种基于鲸鱼优化算法的优化随机森林（WOA-RF）算法，用以开展船舶柴发配电系统故障诊断。
方法首先，基于Matlab/Simulink仿真软件搭建船舶柴发配电系统模型，采集其故障工况和正常工况的数据；然后，对收集的数据进行预处理以提取时域特征，并使用随机森林提取重要特征，从而减少数据维度；最后，使用WOA优化后的随机森林模型对船舶柴发配电系统运行数据进行故障识别、诊断和分类。
结果仿真模拟试验表明：WOA-RF方法识别故障状态和正常状态的准确率为100%，区分12种故障类型的准确率为98.26%；在原始数据集中，与9种不同算法对比，WOA-RF的准确率最低提升了4.86%，最高提升了34.37%；在添加10 dB噪声数据后，与6种不同算法对比，WOA-RF的准确率最低提升了2.43%，最高提升了18.40%。
结论基于WOA-RF的故障诊断方法在复杂海洋环境中展示了优异的准确性和鲁棒性，可为船舶电力系统故障的可靠识别提供参考。
-
关键词:
- 船舶柴发配电系统 /
- Simulink模型 /
- 故障诊断 /
- 鲸鱼优化算法(WOA) /
- 随机森林(RF) /
- 特征提取
Abstract:ObjectivesThe marine diesel generator (DG) power distribution system is crucial for ship navigation. However, due to the harsh marine environment, frequent failures occur. Therefore, a fault diagnosis method based on whale optimization algorithm-optimized random forest (WOA-RF) is proposed for the marine DG power distribution system.
MethodsThe marine DG power distribution system model is built using Matlab/Simulink simulation software. First, fault and normal condition data are collected. Then, the collected data is normalized, time-domain features are extracted, and important features are selected using random forest to reduce data dimensionality. Finally, the WOA-optimized random forest model is used for fault identification, diagnosis and classification.
ResultsSimulation results show that the WOA-RF method can identify fault and normal states with 100% accuracy. It can classify 12 different fault types with an accuracy of 98.26%. In the original dataset, the accuracy of WOA-RF improved by at least 4.86% and by up to 34.37% compared to nine different algorithms. In the dataset with 10 dB noise, the accuracy of WOA-RF improved by at least 2.43% and by up to 18.40% compared to six different algorithms.
ConclusionsThe WOA-RF-based fault diagnosis method demonstrates superior accuracy and robustness in complex marine environments, providing a reliable solution for fault identification in marine power systems.
-
0. 引 言
船舶柴发配电系统是现代船舶的核心组成部分[1]，其可为推进系统、导航设备、通信系统、自动化控制系统及生活区等提供电力支持。随着船舶的主尺度增加和功能复杂化，柴发配电系统也日趋复杂，一旦发生故障，可能导致船舶失去动力或其他关键功能，甚至为船员、货物及航行安全带来风险[2-3]。由于船舶柴发配电系统包含大量的子系统，且各子系统之间具有强耦合性和非线性特征，仅依靠操作人员的经验难以快速准确地定位故障，可能错过最佳排除时机而导致故障加剧，最终影响船舶的机动性和操控性。与陆地发配电系统有所不同[4-5]，船舶柴发配电系统的容量较小且独立性强，任何设备故障都可能引发整个电网的不稳定，尤其在施加或移除较大负荷时，而母线电压波动容易导致严重故障。因此，船舶柴发配电系统对故障诊断和快速响应的要求更高，能否准确定位故障设备并分析原因至关重要。随着技术发展，可实现全船能量整体协调的船舶柴发配电系统将成为未来趋势，为保障航行安全，有必要深入开展故障诊断技术研究[6]。
故障诊断方法分为基于模型和无模型两类：基于模型的方法包括状态估计、参数估计和等价空间法，但船舶电力系统的数学模型一般难以获取，故其应用范围有限；随着计算机技术的发展，无模型故障诊断方法应运而生，例如模糊理论、专家系统、机器学习和深度学习，其无需依赖精确的数学模型，仅利用船舶电网的运行数据即可进行故障诊断[7]，在船舶故障的快速识别、诊断定位等方面具有明显优势。船舶配电系统的数据量庞大，其数据处理设备的计算负荷较高，所以实时故障诊断的难度也较高，因此，迫切需要开发一种不依赖数学模型、可嵌入任何设备和操作系统的算法，不仅可以快速检测故障，还具备区分多种故障类别和故障程度的能力。
目前，在船舶配电系统的故障诊断领域，已开展了大量的研究工作。Zhong等[8]将深度学习应用于船舶柴油机故障诊断，提出了基于相关分布和深度置信网络的方法，并取得了良好的效果。Yu等[9]提出了一种基于改进卷积神经网络的船舶电力系统故障诊断方法。Liu等[10]针对永磁同步电机定子绕组的故障诊断问题，提出了一种改进的粒子群算法，优化了参数选择方式。Li等[11]提出了一种基于电网数据的风电机组故障诊断方法，其利用残差发生器和自主决策建立了长短期记忆网络，可以较好地处理风电机组的时间序列数据。Zhang等[12]针对发电机终端短路故障诊断，提出了一种结合多级小波分解、门控递归神经网络和卷积网络的混合模型，并通过高斯随机变量的合成过采样技术解决了数据不平衡问题。Xie等[13]基于残差网络和双向长短期记忆网络，提出了高阻连接故障的深度学习诊断模型，实现了高性能诊断。Liu等[14]提出了一种基于噪声辅助多元经验模态分解和互信息–轻梯度提升算法的舰船中压直流电力系统故障诊断方法，不仅显著减少了训练时间，还实现了优异的诊断功能。然而，现有的研究成果在以下方面仍有待改进：模型在处理数据类别不平衡时的训练效果欠佳，影响了实际应用效果；高复杂度模型的计算成本较高，限制了其实际应用范围；部分深度学习模型对噪声较为敏感，且在解释性方面存在不足，尤其在标签数据有限的情况下，模型表现将受到明显的制约；此外，在长序列数据建模中，部分方法的处理速度较为缓慢。
针对以上问题，本文拟提出一种鲸鱼优化算法结合随机森林的船舶柴发配电系统故障诊断方法，通过将智能算法与机器学习相结合，从而优化故障诊断过程。首先，通过Simulink仿真软件建立船舶柴发配电系统模型，以模拟正常状态与故障状态，从而生成故障响应曲线并获取数据集；然后，对原始数据进行清洗和归一化处理，进行特征提取，并使用随机森林模型提取重要特征，以减少数据维度；其次，利用鲸鱼优化算法（whale optimization algorithm，WOA）来优化随机森林的关键参数，避免过拟合或欠拟合，以提高模型性能；最后，通过分类准确率、精确率、召回率、F1得分（F1 score，即精确率和召回率的调和平均数）和混淆矩阵对模型性能进行评估，并与其他算法进行对比，从而验证该方法的故障诊断准确率以及处理噪声数据时的鲁棒性。
1. 船舶电力系统
相较于陆地电网而言，船舶电力系统非常特殊，其本质上是一个处于孤岛运行状态的微电网，具有极强的独立性。船舶电网主要分为辐射型、环型和区域配电网络三类，本文的研究对象为环状区域配电网络的柴发配电系统。
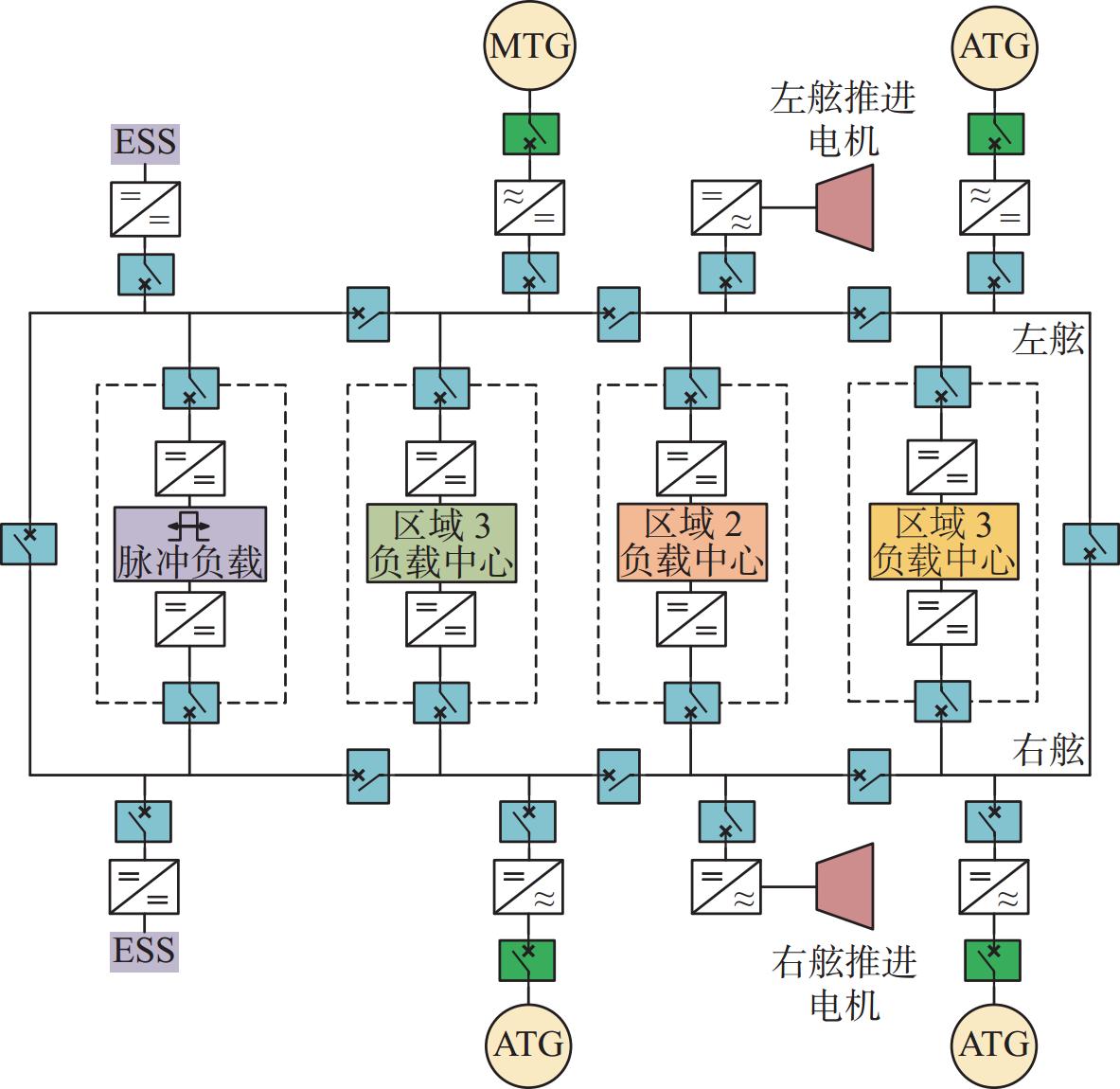
环状区域结构结合了辐射型供电和环型供电的特点，发电机通过配电板形成环状连接。在船舶左舷和右舷分别布置2条母线，艏部和艉部均通过断路器相连，从而将船舶电网划分为多个区域。每个区域均与这2条母线连接，当一侧母线发生故障时，区域内的重要负载将自动切换至另一侧母线，以确保冗余供电，从而提高全船供电的连续性和可靠性，保障船舶的生存力和生命力。图1所示为环状区域配电结构[15]，其中MTG表示主发电机，ATG表示辅发电机，ESS表示能量存储单元。
![]()
图 1 船舶区域配电结构示意图Figure 1. Schematic diagram of ship regional power distribution structure2. 算法理论基础
2.1 随机森林
随机森林（random forest，RF）是一种集成学习算法[16]，其将多棵分类回归树（classification and regression tree，CART）集成在一起，每棵树均针对相同输入进行分类，并通过多数投票确定最终的分类结果。
2.1.1 CART决策树
CART决策树是构成随机森林的基础单元，其使用基尼指数作为属性选择的度量标准。基尼指数可用于衡量数据集的纯度，基尼指数越小，数据集越纯，模型的构建效果也更好。假设数据集D包含n个类别，则基尼指数T(D)的计算公式为
T(D)=1−n∑i=1p2i (1) 式中，pi为第i类元素出现的频率，其中i=1，2，…，n。
根据属性B将数据集D划分为D1和D2，则此时D的基尼系数GB(D)为
GB(D)=|D1||D|GB(D1)+|D2||D|GB(D2) (2) 式中，GB(D1)，GB(D2)分别为D1，D2的基尼系数。
2.1.2 Bagging算法
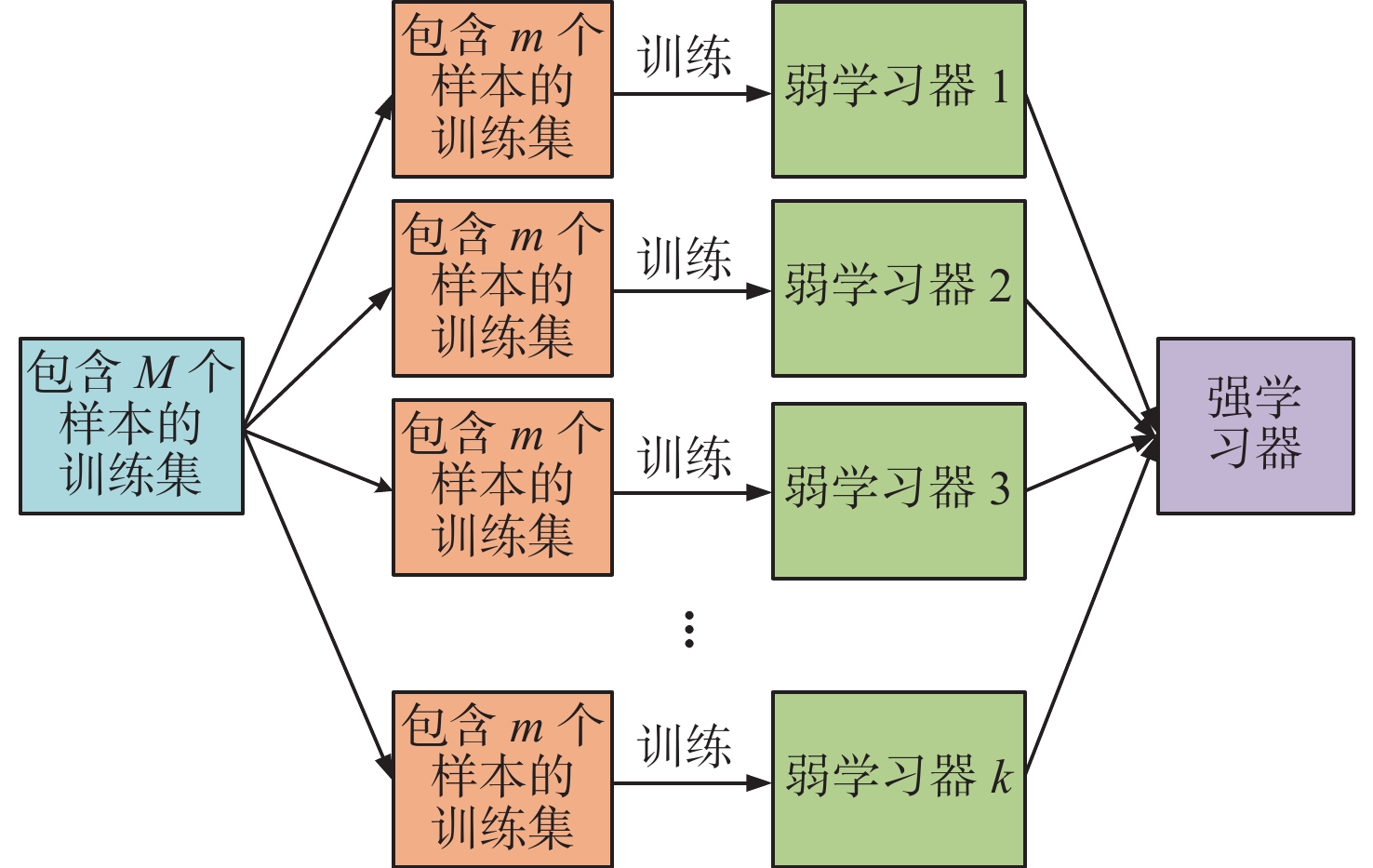
Bagging算法，也称为引导聚集（bootstrap aggregating）算法，是一种并行的集成学习方法，其核心思想是从原始的M个训练样本中反复进行可放回的抽样，每次选取m个样本，从而生成多个不同的训练集，接着训练多个弱学习器。通过对这些弱学习器的结果进行综合，例如投票或平均，来构建一个强学习器，从而提升模型的整体性能和稳定性。图2所示为Bagging算法的原理图
2.1.3 随机森林的计算步骤
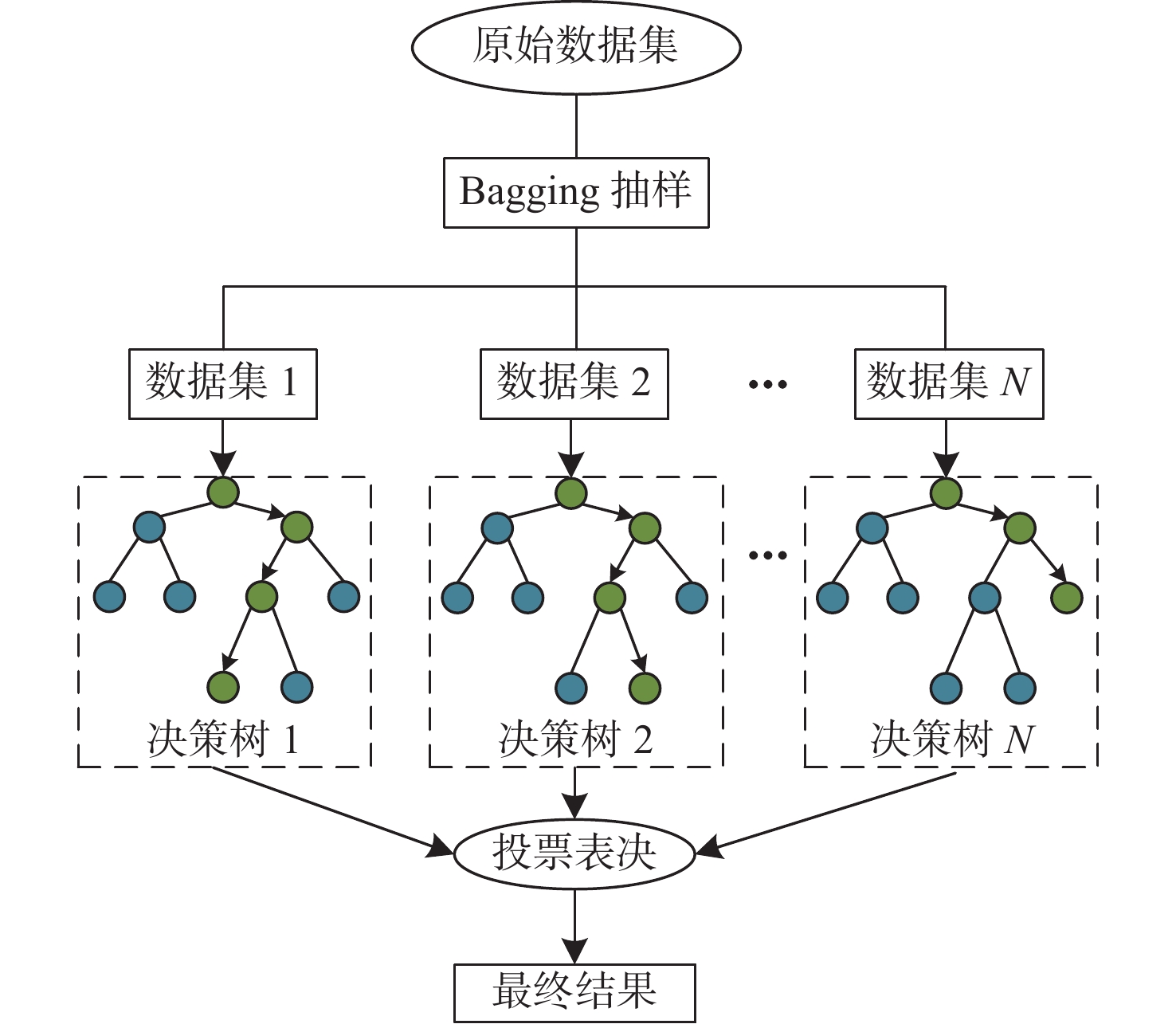
随机森林的计算步骤包括Bagging抽样、决策树基本分类器的构建、决策树投票，如图3所示，其中N表示通过抽样后所生成的数据子集总数。
2.2 鲸鱼优化算法（WOA）
鲸鱼优化算法（WOA）是Mirjalili等[17]于2016年提出的一种新型群体智能优化算法。WOA算法属于元启发式算法，主要通过随机或最佳搜索代理的方式来模拟座头鲸的捕猎行为，并采用螺旋攻击来模拟气泡网的攻击机制。与其他优化算法相比，WOA算法的优化机制简单、寻优能力强且收敛速度快。 WOA算法主要包括3个优化求解过程，即包围猎物、气泡网攻击和随机搜索[18]，具体如下：
1）过程1：包围猎物。
在WOA算法中，鲸鱼群体之间将互相交流信息，并随机游走搜索猎物的位置。每只鲸鱼代表1个个体，每个个体在搜索空间的位置代表1个解。假设当前的最优位置是目标猎物，当群体中其他鲸鱼个体向当前最优个体位置移动时，可利用如下公式来更新位置：
P=|C⋅xbest(t)−x(t)| (3) x(t+1)=xbest(t)−A⋅P (4) 式中：P为目标位置；C和A均为系数向量，且A⋅P为包围步长；x(t)为鲸鱼当前位置，其中t为当前迭代次数，x(t+1)为通过更新规则得到的新位置；xbest(t)为当前全局最优位置。
其中
A=2ar1−a (5) C=2r2 (6) 式中：r1，r2为[0，1]范围内均匀分布的随机数；a为随着迭代次数的增加，从2线性递减至0的收敛因子，即
a=2−2t/tmax (7) 式中， t_{\max} 为最大迭代次数。
2）过程2：气泡网攻击。
在WOA中，鲸鱼通过向上螺旋运动并不断收缩包围圈来攻击猎物，可以采用2种方法来表示鲸鱼的捕食行为，即收缩包围机制和螺旋更新机制。
（1）收缩包围机制：通过减小式（5）和（7）中的收敛因子a即可实现。
（2）螺旋更新位置：鲸鱼以螺线运动轨迹向猎物游动，朝向不同的气泡进行捕食，其数学模型为
x(t + 1) = {P_2}{{\text{e}}^{\beta l}}\cos (2{\text{π }}l) + {x_{{\text{best}}}}(t) (8) 式中： {P_2} = |{x_{{\text{best}}}}(t) - x(t)| ，为鲸鱼与当前全局最优个体之间的距离； \beta 为限定对数螺旋形式的常数；l为[–1，1]区间内的随机数。
当鲸鱼在猎物收缩圈的周围沿着螺旋路径进行游动时，可以选择相同概率的随机变量q进行收缩包围，并通过螺旋更新机制来更新鲸鱼的位置，其数学模型为
x(t+1)=\left\{ \begin{aligned} & {x}_{\text{best}}(t)-A\cdot |C\cdot {x}_{\text{best}}(t)-x(t)|\text{，}&& q < 0.5\\& {P}_{2}{\text{e}}^{\beta l}\mathrm{cos}(2\text{π}l)+{x}_{\text{best}}(t)\text{，}&& q\ge 0.5 \end{aligned}\right. (9) 3）过程3：随机搜索。
在此阶段，随机选择种群的某个鲸鱼个体位置作为目标方向来寻找猎物。当 \left| A \right| \geqslant 1 时，表示鲸鱼在收缩圈外游动，则可根据彼此位置进行随机搜索，其数学表达式如下：
P = |C \cdot {x_{{\text{rand}}}}(t) - x(t)| (10) x(t + 1) = {x_{{\text{rand}}}}(t) - A \cdot P (11) 式中， {x_{{\text{rand}}}}(t) 为种群中随机选取鲸鱼的位置。
在WOA算法中，当控制参数 \left| A \right| < 1 时，进行局部最优解搜索，此时鲸鱼以概率0.5进行猎物包围，以概率0.5进行螺线运动；当控制参数 \left| A \right| \geqslant 1 时，进行全局最优解搜索。
2.3 鲸鱼优化的随机森林算法
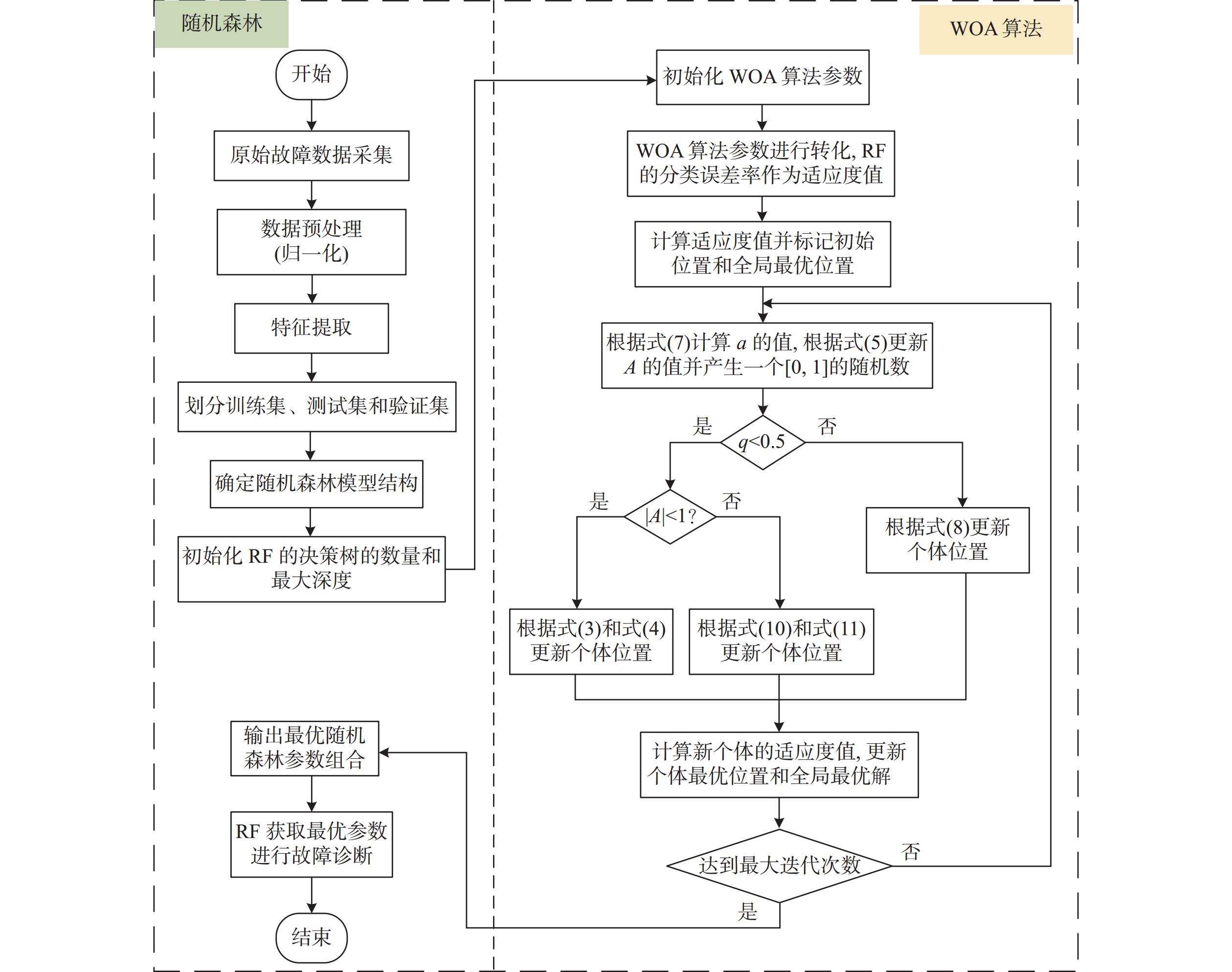
基于鲸鱼优化算法的优化随机森林（whale optimization algorithm-optimized random forest, WOA-RF）算法中，包含了数据收集、数据预处理、特征提取与选择、数据集划分、选择随机森林参数、故障分类、故障评估和故障决策等过程，如图4所示。
![]()
图 4 WOA-RF算法处理的过程框图Figure 4. Block diagram of the process handled by the WOA-RF algorithmWOA-RF算法的分析步骤具体如下：
1）数据收集：收集船舶柴发配电系统在不同短路故障和正常工况下的数据，包括三相电压、三相电流，以及柴油发电机侧的转速、输出功率、励磁电压和电压幅值等10个信号，其中转速、输出功率、励磁电压和电压幅值均以标幺值表示。
2）数据预处理：首先，对原始数据进行清洗和预处理，包括处理缺失值、噪声、异常值；然后，将数据归一化缩放至标准范围（0～1），以防止数据奇异性并提高故障诊断率。
{X^ * } = \frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} (12) 式中：X*为归一化之后的数据；X为原始数据；Xmin，Xmax分别为原始数据中的最小值和最大值。
3）特征提取与选择：首先，从原始数据中提取有意义的时域特征，例如平均值、标准差、最大值、最小值、峰峰值、均方根、振幅因数、波形因数和能量；然后，利用随机森林的重要评估指标来选择具有代表性的特征，以减少数据维度，从而提高模型的性能。
4）数据集划分：将预处理后的数据集划分为70%训练集、20%测试集和10%验证集。
5）选择随机森林参数：在WOA中，每条鲸鱼代表一组随机森林超参数。在适应度评估中，最小误差率作为适应度值，适应度值越低即说明参数组合越优。鲸鱼行为包括包围猎物、螺旋攻击和随机搜索，经过多次迭代来逐步优化超参数，最终输出最佳决策树的数量和深度。图5所示为WOA优化RF参数的寻优流程图。
6）故障分类：采用WOA优化后的随机森林模型对数据进行分类，通过集成多个决策树的预测结果，即可输出最终的分类结果。
7）故障评估：使用验证集评估模型的性能，评估指标包括：准确率、精确率、召回率、F1得分和混淆矩阵。
8）故障决策：根据分类结果和评估指标，做出相应的故障诊断决策（报警机制、维护建议和记录管理）。
2.4 评估指标
在故障分类问题中，需要根据准确率、精确率、召回率和F1得分等指标来评估分类器的性能。根据混淆矩阵，即可计算得出评估指标。混淆矩阵是在机器学习和统计学中用于评估和分类模型的一种表格，如表1所示，混淆矩阵的行和列分别表示实际的类和预测的类。
表 1 混淆矩阵Table 1. Confusion matrix预测为正类别 预测为负类别 真实为正类别 True positive（TP） False negative（FN） 真实为负类别 False positive（FP） True negative（TN） 准确率（accuracy）Ac、精确率（precision）Pr、召回率（recall）Re的定义为
{A_{\text{c}}} = \frac{{{\text{TP + TN}}}}{{{\text{TP + TN + FP + FN}}}} (13) {P_{\text{r}}} = \frac{{{\text{TP}}}}{{{\text{TP + FP}}}} (14) {R_{\text{e}}} = \frac{{{\text{TP}}}}{{{\text{TP + FN}}}} (15) 作为精确率和召回率的调和平均数，F1得分的表达式为
F1 = \frac{{2{P_{\text{r}}} \cdot {R_{\text{e}}}}}{{P{P_{\text{r}}} + {R_{\text{e}}}}} (16) 3. 实验和结果分析
3.1 故障数据获取
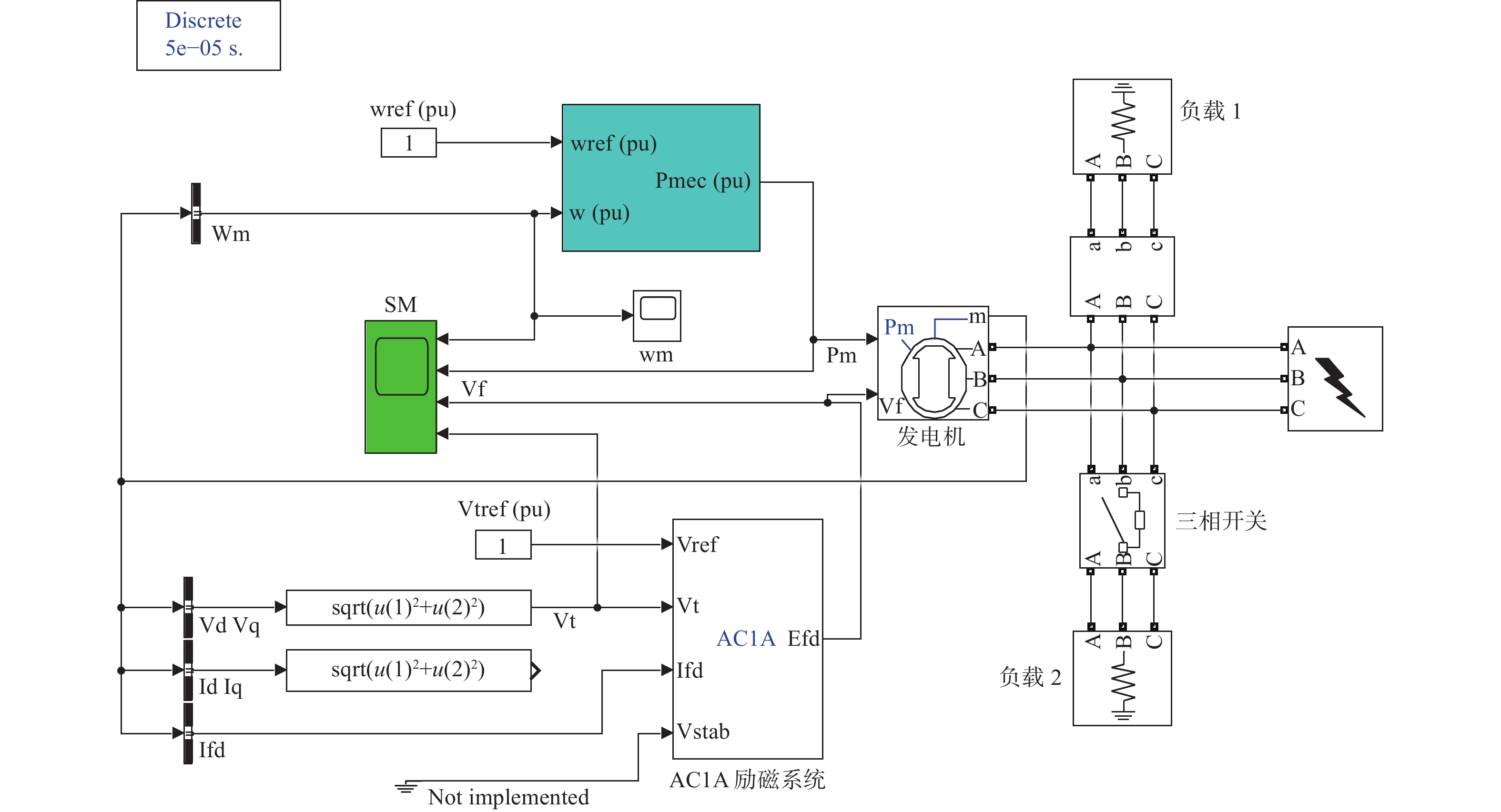
本文以Matlab 2023b作为仿真软件，操作系统为Windows11，计算机为i5-13400F，2.5 GHz，内存32 GB。在Matlab/Simulink中搭建船舶柴发配电系统模型[19]，如图6所示，具体参数如表2所示。
表 2 模型参数Table 2. Model parameter参数名称 数值 额定功率Pn/MW 6 额定电压Ul/V 660 定子电阻Rs/Ω 0.003 6 额定频率fn/Hz 50 惯性系数H(s)/s 1.07 极对数P 4 d轴同步电抗 X_{\text{d}} /pu 1.26 d轴暂态同步电抗 X'_{\text{d}} /pu 0.213 d轴次暂态同步电抗 X''_{\text{d}} /pu 0.111 q轴同步电抗 X_{\text{q}} /pu 0.70 q轴次暂态同步电抗 X''_{\text{q}} /pu 0.122 漏电抗 X_{\text{l}} /pu 0.067 d轴暂态时间常数 T' /s 0.32 d轴次暂态时间常数 {T''_{\text{d}}} /s 0.015 q轴次暂态时间常数 {T''_{\text{q}}} /s 0.30 通过改变故障发生器的类型，即可模拟不同种类的故障类型，最终得到11类故障工况和1种正常工况下的仿真数据（共计12种），故障类型所对应的标签如表3所示。设定本文的故障点均为负载侧发生的故障，故需采集负载侧的三相电压、三相电流以及柴油同步发电机侧的转速、功率、励磁电压和电压幅值并进行特征提取，其中转速、功率、励磁电压和电压幅值均采用标幺值表示。
表 3 故障类型所对应的标签Table 3. Fault categories and labels故障类别 标签 A相接地故障 1 B相接地故障 2 C相接地故障 3 AB相相间短路故障 4 BC相相间短路故障 5 CA相相间短路故障 6 AB相两相接地故障 7 BC相两相接地故障 8 CA相两相接地故障 9 ABC三相短路故障 10 ABC三相接地故障 11 正常工况 12 假设每个工况的运行时间为15 s，采样频率为20 kHz，每组数据有300 000个采样点。本文接入的负载共有3种组合，如表4所示：组合1为1 MW和0 MW；组合2为3 MW和1 MW；组合3为0.5 MW和5.5 MW。负载接入的时间为分别为第5 s和第10 s，持续时间为5 s，即第1种情况为负载第5 s时接入，第10 s时断开；第2种情况为负载第10 s时接入，持续到仿真结束。设定故障发生的时间分别为第1，4，7，10 s，故障的持续时间为0.1，0.2，0.3，0.4，0.5 s。综合以上条件，1种故障类型有120组数据，则11种故障工况和1种正常工况共有
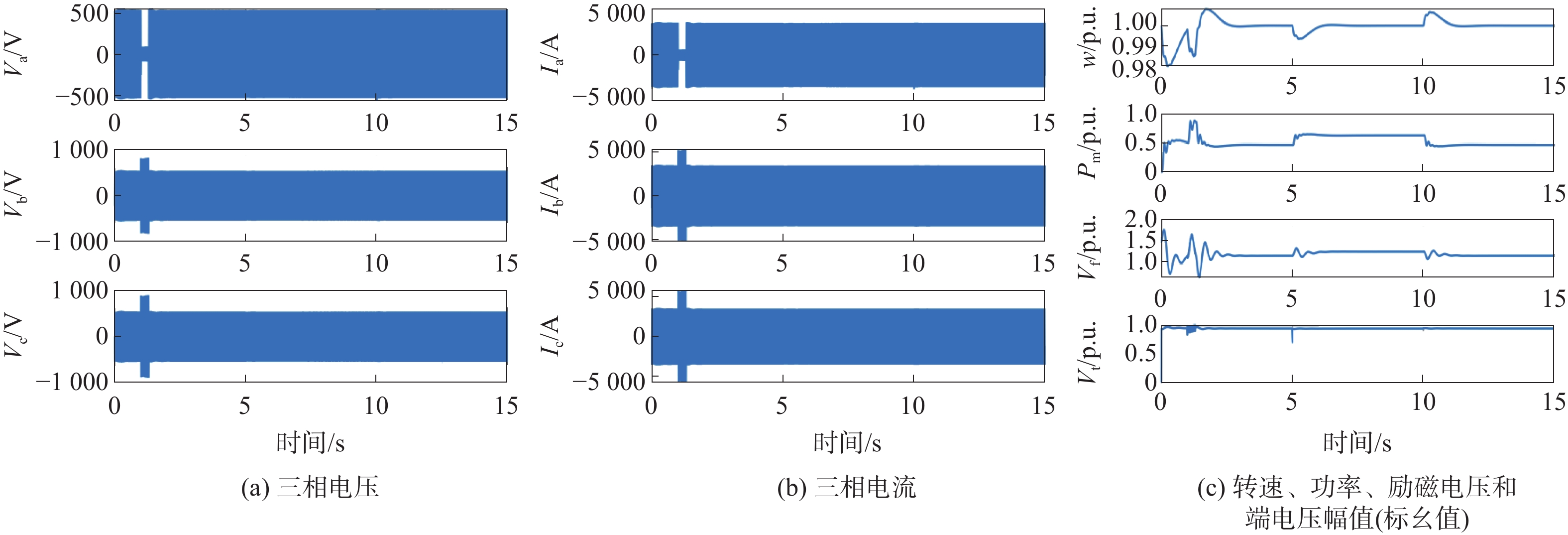
1440 组数据。表 4 负载接入表Table 4. Load access table组合序号 负载一/MW 负载二/MW 1 1 0 2 3 1 3 0.5 5.5 图7表示A相接地故障中一组数据的10个信号的故障波形图。结合负载处电压、电流变化情况以及发电机输出端的变化情况可知，第1 s时，发电机侧A相发生接地短路故障：图7（a）中，负载处的A相电压Va瞬间减小，电压值接近于0，其余两相电压（Vb和Vc）均出现了相同幅度的增加；图7（b）中，A相电流Ia瞬间减小，其余两相电流（Ib和Ic）的增加幅度相同；图7（c）中，发生故障后的转速w和功率Pm先突增尔后保持稳定，励磁电压Vf和端电压Vt均保持稳定，无明显变化。
3.2 故障诊断结果分析
为了确定最佳参数，在提取特征之后，采用WOA算法选择RF的超参数，并将最大化准确率（即最小化错误率）作为适应度函数值。WOA的参数设置为：种群数量为20，最大迭代次数为100，上下限值为[0，100]，维度为2。
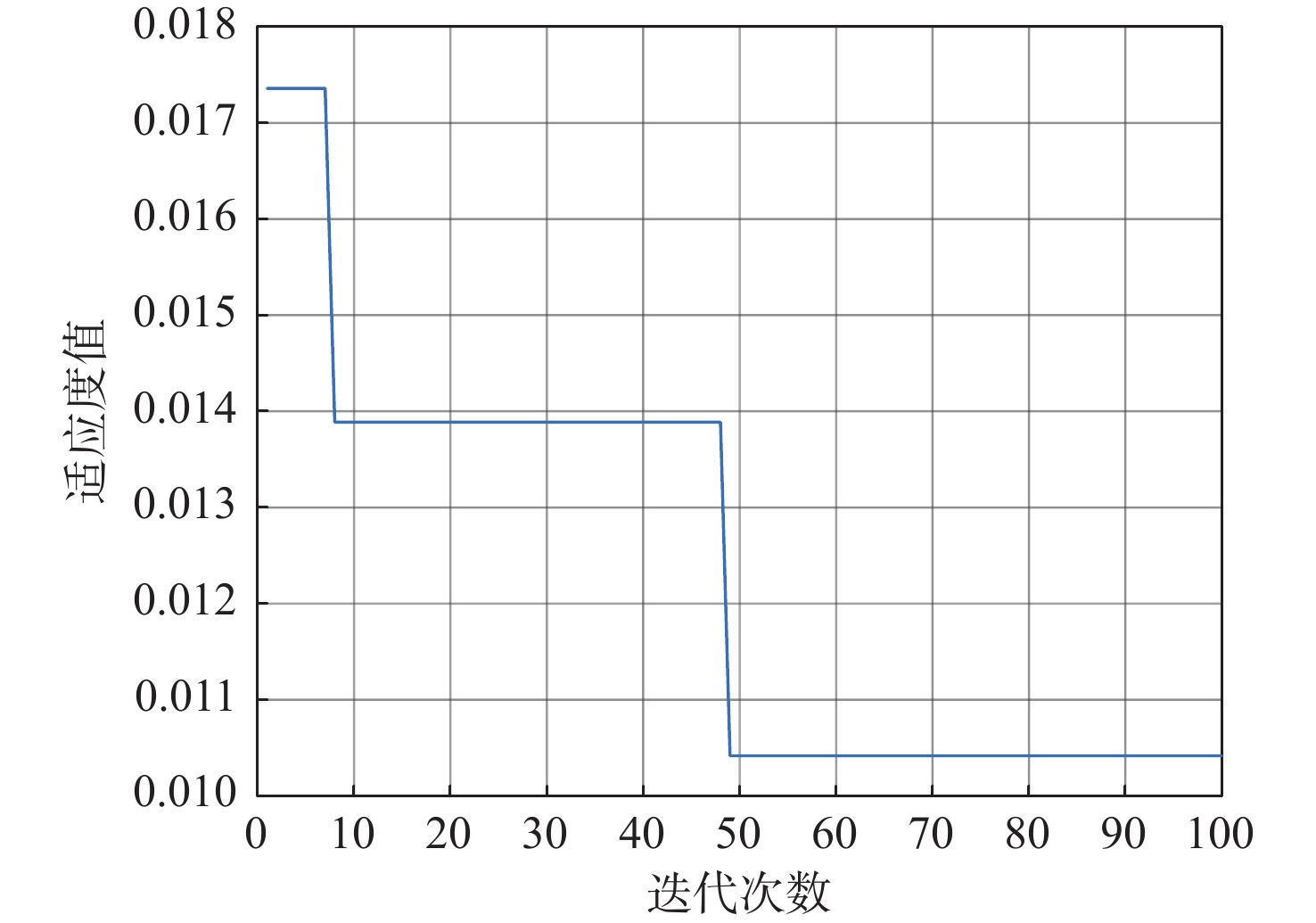
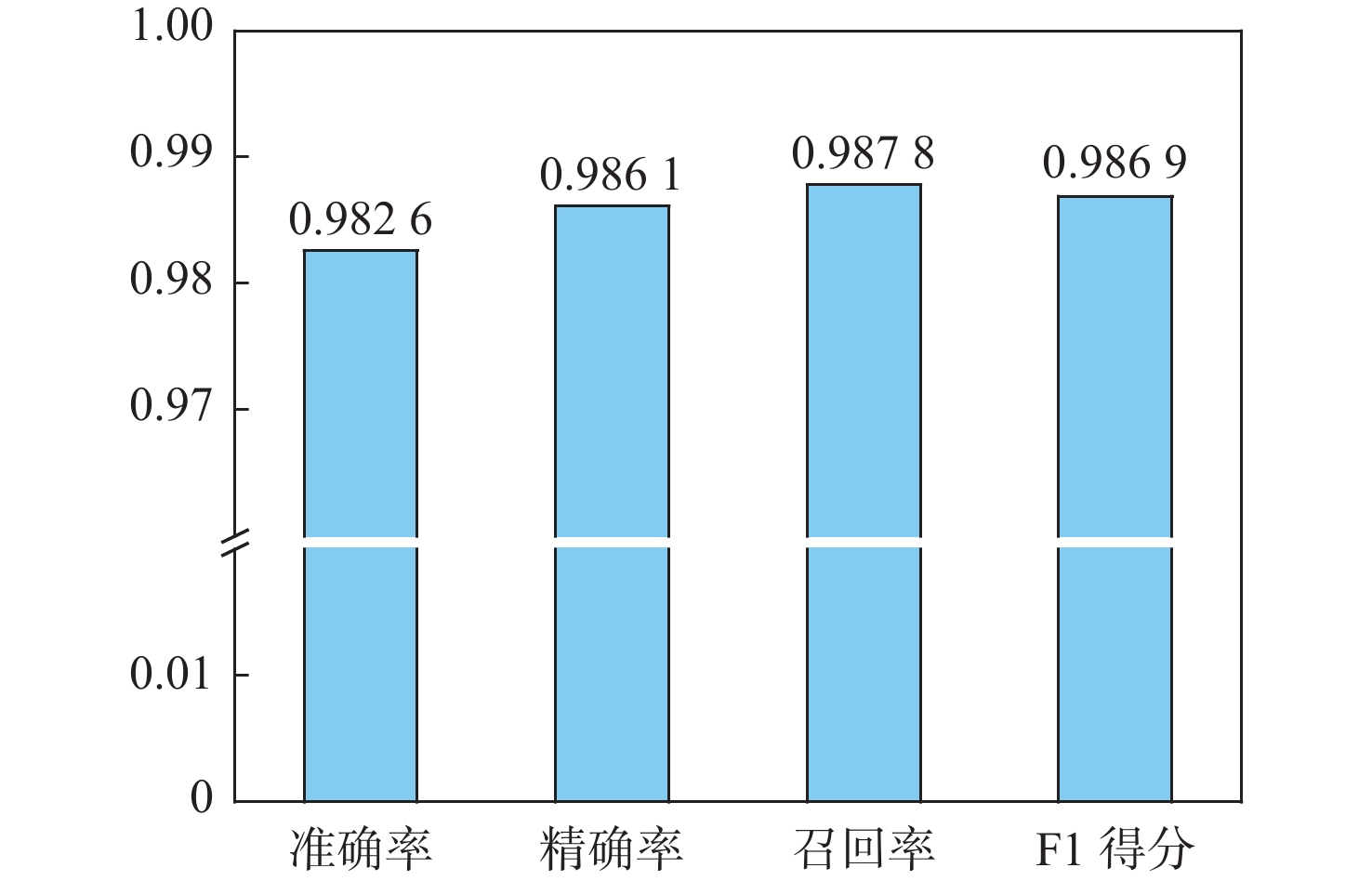
WOA-RF仿真计算结果如图8所示，可知WOA-RF算法在迭代过程中表现了较好的收敛性，经过48次迭代后，适应度值达到最优。当完成100次迭代后，输出了优化所得的2个超参数，即决策树的数量和最大深度，以此作为随机森林的超参数。然后，在船舶柴发配电系统的故障原始数据集上进行WOA-RF故障诊断和故障分类，验证集数据集的实验结果如图9所示，WOA-RF的准确率为98.26%，精确率为98.61%，召回率为98.78%，F1得分为98.69%。
为了进一步验证WOA-RF算法的有效性，将WOA-RF与9种算法进行比较，包括K近邻算法（K-nearest neighbors，KNN）、支持向量机（support vector machine，SVM）、反向传播算法（backpropagation， BP）、随机森林（random forest，RF）、学习向量量化（learning vector quantization，LVQ）、决策树（decision tree，DT）、集成学习（ensemble learning，EL）、极限学习机（extreme learning machine，ELM）和卷积神经网络（convolutional neural network，CNN）。表5所示为以准确率、精确率、召回率和F1得分（F1_Score）作为评估指标的不同算法对比结果。
表 5 WOA-RF与其他算法的4种指标对比Table 5. Comparison of four indicators between WOA-RF and other algorithms算法 评估指标 准确率 精确率 召回率 F1得分 KNN 86.11% 85.52% 84.57% 84.45% SVM 72.57% 73.38% 84.31% 76.28% BP 63.89% 66.19% 66.23% 63.94% RF 90.36% 90.17% 90.25% 90.02% LVQ 74.65% 73.38% 73.20% 71.92% EL 93.40% 92.82% 92.80% 92.81% ELM 86.84% 86.31% 87.26% 86.78% CNN 91.67% 92.07% 91.88% 91.98% DT 94.44% 94.20% 94.18% 94.19% WOA-RF 98.26% 98.61% 98.78% 98.69% 由表5得知，本文WOA-RF算法的准确率为98.26%，与KNN（86.11%）相比，提高了12.15%；与SVM（72.57%）相比，提高了25.69%；与BP（63.89%）相比，提高了34.37%；与RF（90.36%）相比，提高了7.9%；与LVQ（74.65%）相比，提高了23.61%；与ELM（86.84%）相比，提高了11.42%；与CNN（91.67%）相比，提高了6.59%；与EL（93.40%）相比，提高了4.86%；与准确率最高的DT（94.44%）相比，提高了3.82%，由此可见，WOA-RF算法的准确率平均提高了14.55%。同样，在精确率方面，WOA-RF算法最少提高了4.41%（相较于DT），最多提高了32.42%（相较于BP），平均提高了14.83%；在召回率方面，WOA-RF最少提高了4.60%（相较于DT），最多提高了32.55%（相较于BP），平均提高了13.82%；在F1得分方面，WOA-RF最少提高了4.5%（相较于DT），最多提高了34.75%（相较于BP），平均提高了15.09%。
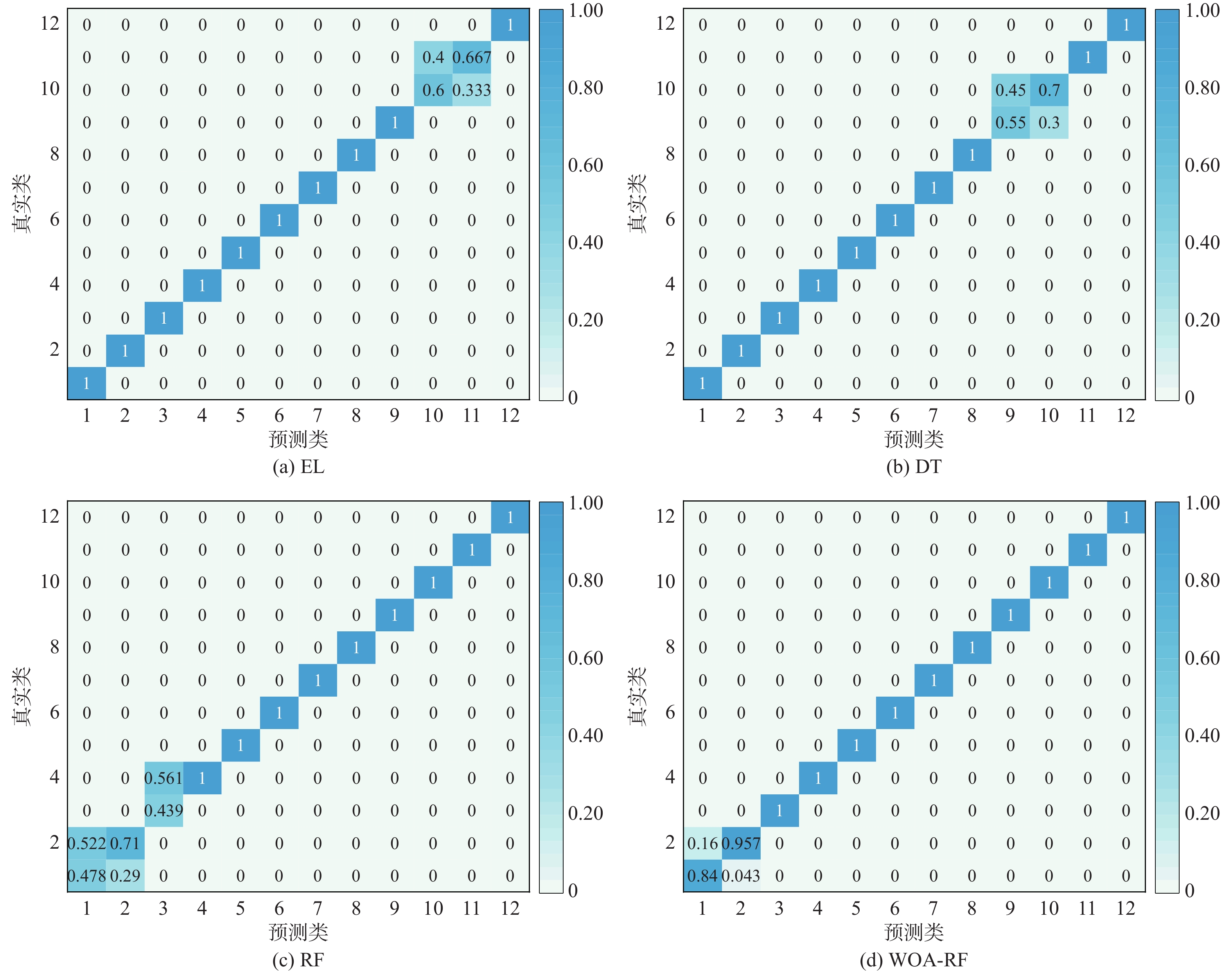
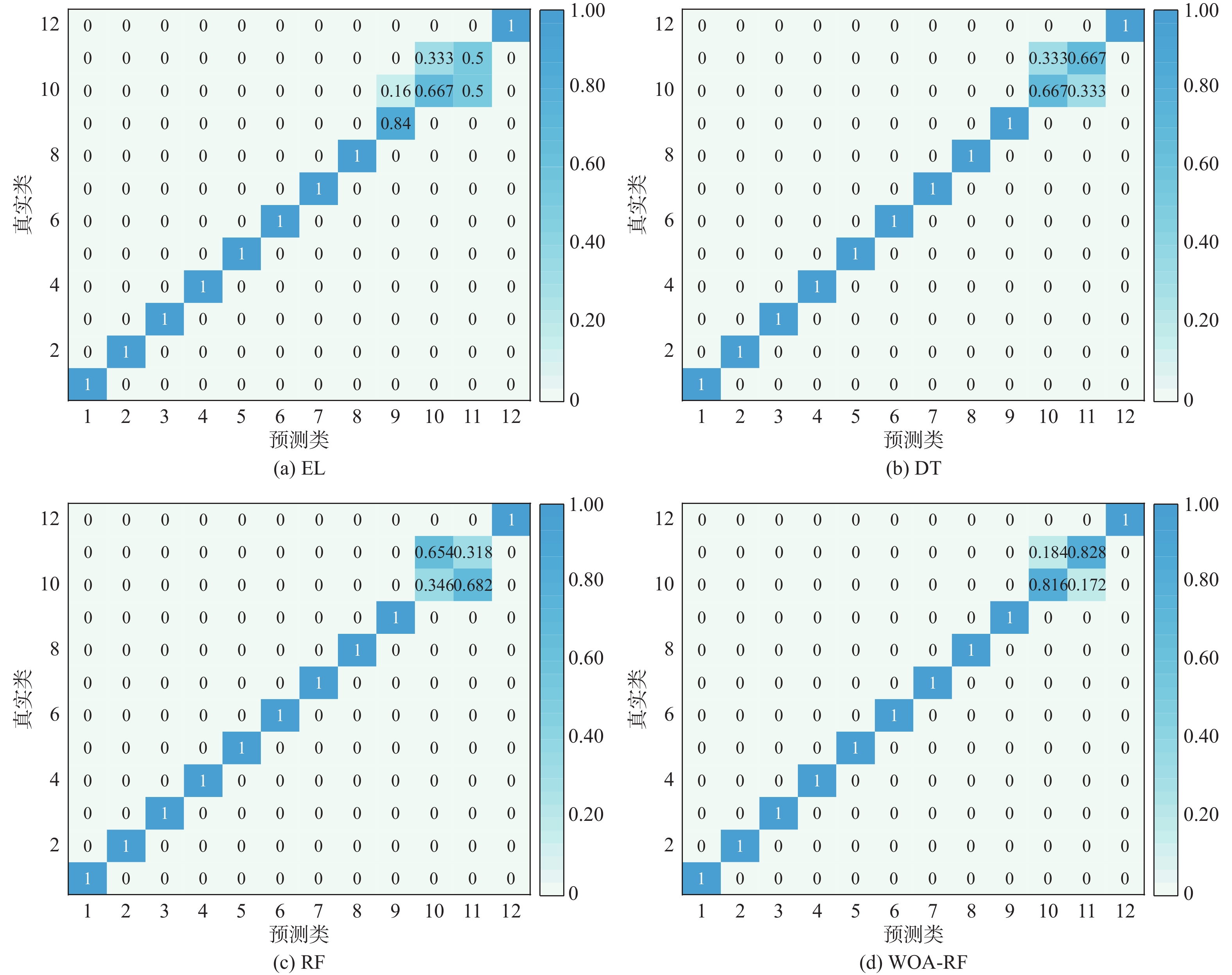
图10所示为不同算法验证集的混淆矩阵，其中坐标轴数字1～12分别表示故障类型所对应的标签，右侧0～1标尺表示混淆矩阵数值经归一化处理后，反映模型在各个类别上的准确率和错误率。由图10（a）可知，标签10和标签11的诊断率分别为60%和66.7%，而其他标签的诊断率均为100%；由图10（b）可知，标签9和标签10的诊断率分别为55%和70%，而其他标签的诊断率均为100%；由图10（c）可知，标签1、标签2和标签3的诊断率分别为47.8%、71%和43.9%，其他标签的诊断率均为100%；由图10（d）得知，标签1的诊断率为84%，标签2的诊断率为95.7%，而标签3至标签12的诊断率为100%。
由此可见，WOA-RF算法的故障诊断准确率很高，明显优于RF算法、EL算法和DT算法，不仅可以区分正常工况和故障工况，还能识别不同的故障类别。
在船舶电力系统中，故障诊断是保障系统安全运行的关键环节。然而，在实际操作环境中存在各种复杂的干扰因素，例如传感器精度限制、环境噪声和信号传输误差等，这些因素可能导致系统获取的数据带有不同程度的噪声，从而影响故障诊断的准确性和可靠性。为了模拟这些实际工况，评估诊断模型在噪声条件下的鲁棒性，有必要开展引入噪声的实验。
当完成对船舶柴发配电系统故障数据的基础分析之后，为进一步验证诊断模型的鲁棒性和实际应用效果，下一步将开展噪声添加实验。通过在船舶柴发配电系统故障数据中添加不同水平的噪声，可以有效模拟现实环境中可能出现的各种干扰情况。该实验不仅有助于揭示噪声对诊断结果的影响，还可为优化及提升故障诊断模型的抗干扰能力提供依据，从而为确保船舶柴发配电系统在复杂和多变的实际运行环境中保持高效、可靠的故障诊断能力奠定基础。
通过对原始数据添加10 dB噪声，并采用与上文相同的处理方式，即可得到如图11所示的不同算法验证集的混淆矩阵。
![]()
图 11 添加噪声条件下的验证数据集混淆矩阵Figure 11. Confusion matrix of validation data set under added noise由图11（a）得知，标签9、标签10和标签11的诊断率分别为84%，66.7%，50%，而其他标签的诊断率均为100%；由图11（b）得知，标签10和标签11的诊断率均为66.7%，其他标签的诊断率均为100%；由图11（c）得知，标签10和标签11的诊断率分别为34.6%和31.8%，其他标签的诊断率均为100%；由图11（d）得知，WOA-RF算法已经达到100%的故障识别率，在具体故障类别的识别过程中，仅标签10和标签11的诊断率分别为81.6%和82.8%。因此，添加噪声后的WOA-RF算法在故障诊断方面仍然具有很高的准确率，明显优于RF算法、EL算法和DT算法，不仅可区分正常工况和故障状态，还能识别不同的故障类别。
为了进一步验证WOA-RF算法的有效性，本节将WOA-RF与KNN算法、BP算法、RF算法、ELM算法、EL算法、DT算法进行对比分析，根据准确率、精确率、召回率和F1得分进行验证和评估，结果如表6所示。
表 6 WOA-RF与其他算法的4种指标对比（添加噪声后）Table 6. Comparison of four indicators between WOA-RF and other algorithms（after adding noise）算法 评估指标 准确率 精确率 召回率 F1得分 KNN 78.47% 78.37% 77.99% 76.88% BP 76.74% 77.30% 76.94% 76.18% RF 88.89% 90.83% 88.88% 88.87% ELM 89.61% 86.64% 86.82% 86.73% EL 92.01% 91.56% 91.57% 91.56% DT 92.71% 92.51% 92.48% 92.36% WOA-RF 95.14% 95.36% 95.30% 95.28% 分析表6可知，添加噪声后的数据准确率略低于原始数据（表5），但下降幅度较小，WOA-RF算法的准确率为95.14%，与KNN（78.47%）相比，提高了16.67%；与BP（76.74%）相比，提高了18.40%；与RF（88.89%）相比，提高了6.25%；与ELM（89.61%）相比，提高了5.53%；与EL（92.01%）相比，提高了3.13%；与准确率最高的DT（92.71%）相比，提高了2.43%，即WOA-RF算法的平均准确率提高了8.735%。在精确率方面，WOA-RF算法至少提高了2.85%（相较于DT），最多提高了18.06%（相较于BP），平均提高了9.16%；在召回率方面，WOA-RF算法最少提高了2.82%（相较于DT），最多提高了18.36%（相较于BP），平均提高了9.58%；在F1得分方面，WOA-RF最少提高了2.92%（相较于DT），最多提高了19.1%（相较于BP），平均提高了9.85%。
4. 结 论
传统的故障诊断方法依赖于先验知识和专家经验，需要构建精确的数学模型，故难以应对系统设备的新变化和未知故障，其扩展性和适应性有限。相比之下，基于数据驱动的故障诊断采用机器学习与深度学习，能够处理复杂系统以及非线性关系，具有较好的泛化能力，但存在样本难获取、训练时间长等问题，难以满足实时性要求。为此，本文提出了一种基于鲸鱼优化算法与随机森林结合的船舶柴发配电系统故障诊断方法，并通过Matlab/Simulink仿真平台建立了船舶电力系统模型，进而提取故障特征，并利用鲸鱼优化算法对随机森林超参数进行优化，仿真结果表明：WOA-RF方法可以有效识别系统的故障工况和正常工况，故障识别率高达100%；在原始数据集下对12种故障类型的诊断准确率为98.26%，在噪声数据集下的准确率为95.14%；与其他算法相比，WOA-RF在准确率、精确率、召回率和F1得分等指标方面均有显著的提升效果。这表明该算法不仅具备较高的故障诊断准确率，还在噪声环境下保持了良好的鲁棒性，所以具备良好的应用潜力。
需注意的是，虽然WOA-RF算法在船舶柴发配电系统故障诊断中表现优异，但该方法仍存在一定的优化空间：
1）计算复杂度高：由于WOA在迭代过程中涉及多次全局搜索和适应度评估，尤其在处理大规模数据集时，WOA-RF算法的计算复杂度较高，故导致训练时间较长，难以满足实时性要求。
2）收敛性问题：虽然WOA在大多数情况下表现了良好的优化效果，但仍可能存在收敛速度较慢或陷入局部最优解的问题，所以其在复杂环境下的诊断效果有限。
在未来的研究工作中，可以通过降低WOA-RF的计算复杂度来优化算法效率，具体方法包括改进WOA的搜索机制或引入并行计算技术，从而加快大规模数据集的处理速度，以更好地满足实时性需求。同时，可以结合其他优化算法的局部优化能力与WOA的全局搜索优势来形成混合优化策略，以加快收敛速度，从而提升算法在复杂故障诊断中的鲁棒性与全局搜索能力。此外，WOA-RF算法还可以进一步增强其在实际工程中的实用性与适应性，例如扩展到其他电力系统，为其提供新的故障诊断思路。
-
![]()
图 1 船舶区域配电结构示意图
Figure 1. Schematic diagram of ship regional power distribution structure
![]()
图 4 WOA-RF算法处理的过程框图
Figure 4. Block diagram of the process handled by the WOA-RF algorithm
![]()
图 11 添加噪声条件下的验证数据集混淆矩阵
Figure 11. Confusion matrix of validation data set under added noise
表 1 混淆矩阵
Table 1 Confusion matrix
预测为正类别 预测为负类别 真实为正类别 True positive（TP） False negative（FN） 真实为负类别 False positive（FP） True negative（TN） 
下载: 导出CSV
表 2 模型参数
Table 2 Model parameter
参数名称 数值 额定功率Pn/MW 6 额定电压Ul/V 660 定子电阻Rs/Ω 0.003 6 额定频率fn/Hz 50 惯性系数H(s)/s 1.07 极对数P 4 d轴同步电抗 X_{\text{d}} /pu 1.26 d轴暂态同步电抗 X'_{\text{d}} /pu 0.213 d轴次暂态同步电抗 X''_{\text{d}} /pu 0.111 q轴同步电抗 X_{\text{q}} /pu 0.70 q轴次暂态同步电抗 X''_{\text{q}} /pu 0.122 漏电抗 X_{\text{l}} /pu 0.067 d轴暂态时间常数 T' /s 0.32 d轴次暂态时间常数 {T''_{\text{d}}} /s 0.015 q轴次暂态时间常数 {T''_{\text{q}}} /s 0.30
下载: 导出CSV
表 3 故障类型所对应的标签
Table 3 Fault categories and labels
故障类别 标签 A相接地故障 1 B相接地故障 2 C相接地故障 3 AB相相间短路故障 4 BC相相间短路故障 5 CA相相间短路故障 6 AB相两相接地故障 7 BC相两相接地故障 8 CA相两相接地故障 9 ABC三相短路故障 10 ABC三相接地故障 11 正常工况 12
下载: 导出CSV
表 5 WOA-RF与其他算法的4种指标对比
Table 5 Comparison of four indicators between WOA-RF and other algorithms
算法 评估指标 准确率 精确率 召回率 F1得分 KNN 86.11% 85.52% 84.57% 84.45% SVM 72.57% 73.38% 84.31% 76.28% BP 63.89% 66.19% 66.23% 63.94% RF 90.36% 90.17% 90.25% 90.02% LVQ 74.65% 73.38% 73.20% 71.92% EL 93.40% 92.82% 92.80% 92.81% ELM 86.84% 86.31% 87.26% 86.78% CNN 91.67% 92.07% 91.88% 91.98% DT 94.44% 94.20% 94.18% 94.19% WOA-RF 98.26% 98.61% 98.78% 98.69%
下载: 导出CSV
表 6 WOA-RF与其他算法的4种指标对比（添加噪声后）
Table 6 Comparison of four indicators between WOA-RF and other algorithms（after adding noise）
算法 评估指标 准确率 精确率 召回率 F1得分 KNN 78.47% 78.37% 77.99% 76.88% BP 76.74% 77.30% 76.94% 76.18% RF 88.89% 90.83% 88.88% 88.87% ELM 89.61% 86.64% 86.82% 86.73% EL 92.01% 91.56% 91.57% 91.56% DT 92.71% 92.51% 92.48% 92.36% WOA-RF 95.14% 95.36% 95.30% 95.28%
下载: 导出CSV
-
[1] KJONG S, RØDSKAR E, MOLINAS M, et al. The marine vessel's electrical power system: from its birth to present day[J]. Proceedings of the IEEE, 2015, 103(12): 2410–2424. doi: 10.1109/JPROC.2015.2496722
[2] 李维波, 郝春昊, 高佳俊, 等. 舰船综合电力系统发展综述[J]. 中国舰船研究, 2020, 15(6): 1–11. doi: 10.19693/j.issn.1673-3185.01682 LI W B, HAO C H, GAO J J, et al. Overview of the development of shipboard integrated power system[J]. Chinese Journal of Ship Research, 2020, 15(6): 1–11 (in Chinese). doi: 10.19693/j.issn.1673-3185.01682
[3] BARROS J, DIEGO R I. A review of measurement and analysis of electric power quality on shipboard power system networks[J]. Renewable and Sustainable Energy Reviews, 2016, 62: 665–672. doi: 10.1016/j.rser.2016.05.043
[4] 孙光甦, 原宗, 关静. 舰船综合保障体系综述[J]. 中国舰船研究, 2020, 15(1): 89–94. doi: 10.19693/j.issn.1673-3185.01585 SUN G S, YUAN Z, GUAN J. A review of integrated logistics support systems for ships[J]. Chinese Journal of Ship Research, 2020, 15(1): 89–94 (in Chinese). doi: 10.19693/j.issn.1673-3185.01585
[5] ZHANG Z, HE X. Fault-structure-based active fault diagnosis: a geometric observer approach[J]. Energies, 2020, 13(17): 4475. doi: 10.3390/en13174475
[6] WANG Z, XIA L, WANG Y J, et al. Fault diagnosis system based on multiagent technique for ship power system[J]. Mathematical Problems in Engineering, 2014, 2014(1): 370246. doi: 10.1155/2014/370246
[7] GAO Z W, CECATI C, DING S X. A survey of fault diagnosis and fault-tolerant techniques—Part I: fault diagnosis with model-based and signal-based approaches[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757–3767. doi: 10.1109/TIE.2015.2417501
[8] ZHONG G Q, WANG H Y, ZHANG K Y, et al. Fault diagnosis of marine diesel engine based on deep belief network[C]//Proceedings of 2019 Chinese Automation Congress. Hangzhou, China: IEEE, 2019: 3415-3419. doi: 10.1109/CAC48633.2019.8997060.
[9] YU C C, QI L, SUN J, et al. Fault diagnosis technology for ship electrical power system[J]. Energies, 2022, 15(4): 1287. doi: 10.3390/en15041287
[10] LIU W X, LIU L, CHUNG I Y, et al. Modeling and detecting the stator winding fault of permanent magnet synchronous motors[J]. Simulation Modelling Practice and Theory, 2012, 27: 1–16. doi: 10.1016/j.simpat.2012.04.007
[11] LI M S, YU D, CHEN Z M, et al. A data-driven residual-based method for fault diagnosis and isolation in wind turbines[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 895–904. doi: 10.1109/TSTE.2018.2853990
[12] ZHANG L Y, ZHANG Z Q, PENG H M. Diagnostic method for short circuit faults at the generator end of ship power systems based on MWDN and deep-gated RNN-FCN[J]. Journal of Marine Science and Engineering, 2023, 11(9): 1806. doi: 10.3390/jmse11091806
[13] XIE J L, SHI W F, XUE T, et al. High-resistance connection fault diagnosis in ship electric propulsion system using res-CBDNN[J]. Journal of Marine Science and Engineering, 2024, 12(4): 583. doi: 10.3390/jmse12040583
[14] LIU S, SUN Y, ZHANG L Y, et al. Fault diagnosis of shipboard medium-voltage DC power system based on machine learning[J]. International Journal of Electrical Power & Energy Systems, 2021, 124: 106399. doi: 10.1016/j.ijepes.2020.106399
[15] AMY J V. Considerations in the design of naval electric power systems[C]//Proceedings of the IEEE Power Engineering Society Summer Meeting. Chicago: IEEE, 2002: 331-335. doi: 10.1109/PESS.2002.1043244.
[16] 周海军, 王超伟, 周国敬, 等. 基于随机森林的离心泵滚动轴承故障诊断[J]. 中国舰船研究, 2020, 15(3): 129–135. doi: 10.19693/j.issn.1673-3185.01646 ZHOU H J, WANG C W, ZHOU G J, et al. Fault diagnosis of antifriction bearing of centrifugal pump based on random forest[J]. Chinese Journal of Ship Research, 2020, 15(3): 129–135 (in Chinese). doi: 10.19693/j.issn.1673-3185.01646
[17] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008
[18] 王喜莲, 秦嘉翼, 耿民. 基于d-q变换及WOA-LSTM的异步电机定子匝间短路故障诊断方法[J]. 电机与控制学报, 2024, 28(6): 56–65. doi: 10.15938/j.emc.2024.06.006 WANG X L, QIN J Y, GENG M. Asynchronous motor stator turn-to-turn short circuit fault diagnosis based on d-q transform and WOA-LSTM[J]. Electric Machines and Control, 2024, 28(6): 56–65 (in Chinese). doi: 10.15938/j.emc.2024.06.006
[19] 张峰. 船舶电力系统故障分析及诊断技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2022. ZHANG F. Research on fault analysis and diagnosis technology of ship power system[D]. Harbin: Harbin Engineering University, 2022 (in Chinese).
计量
- 文章访问数: 60
- HTML全文浏览量: 22
- PDF下载量: 1
