0.   引　言

自主水下航行器（AUV）由于具有体积小、成本低、探测范围大、自主性高等特点，被广泛应用于观测、防卫、通信等作业场景^[1-2]。上世纪末，已有超过66种AUV处于应用或者在研中^[3]。无论是AUV接收岸基信号完成指定作业任务，还是将AUV作为信号中继站搭建海洋通信网络，对其通信能力均提出了要求，如何解决AUV的通信问题成为国内外无人水下领域的重点。

水声通信是目前发展最成熟、应用最广泛的水下无线通信技术。声波在水下信号衰减较小，传输距离远。黄海等^[4]基于信道传输模型对AUV间的信号传输方式进行优化，改进了AUV编队的组网通信方法，降低了信号传输的丢包率和领航AUV的耗能；王小阳等^[5]提出基于模数转换变采样抑制多普勒的AUV移动通信方案，直接对信号进行多普勒补偿，改善了水声实时通信的质量。但无论是对于AUV组网信号传输方式的优化，还是对于移动水声信号调制在算法层面的改进，都无法解决水声通信隐蔽性低、带宽有限的问题。此外，水声系统设备成本高、体积大、耗能多，对于小型AUV而言装配难度较高。

海水对于波长为400～550 nm的蓝绿光存在低损耗窗口^[6]，这一“蓝绿光透过窗口”让水下光学通信成为可能。Schill等^[7]开发了一种通过蓝（460 nm）、青（490 nm）、绿（520 nm）三色光进行通信的光学通信系统，成本低、体积小、稳定性较高，通信速率可达57.6 kbit/s；Bales^[8]研制了基于发光二极管的低功率深海水下光学通信系统，其通过采用键控调制技术，增大了带宽，通信速率可达10 Mbit/s。但上述2种研究在信号衰减方面仍然存在问题：前者采用红外无线通信协议，传输距离不足5 m；后者未考虑光学信道的散射影响，研究结果仅适用于深海，在浅海、近水面空间、跨介质等AUV常见通信场景中光波衰减更大。

电磁波通信、磁感应通信与光学通信一样，缺点是在海水中传输衰减较大，无法突破传输距离的限制。除了针对不同信息载体的通信研究外，有关硬件和通信模式的改进在潜艇的通信领域中较为成熟。潜艇等较大的水下平台直接上浮通信具有较大的暴露风险，利用浮标进行通信是较为高效的通信方式。例如，美国“俄亥俄”级核潜艇装备了AN/BRR-6B型拖拽通信浮标系统，其利用光缆将浮标放出并上浮至海面进行通信，而潜艇则悬浮于水面下100～200 m处。但浮标系统规模较大，难以装配在尺度较小的AUV上。

Dala等^[9]设计了能够在水面和水下应用于远距离通信的天线，研究发现在868 MHz下水面通信的信号传输距离是水下通信信号传输距离的25倍以上，验证了通信场景从水下转变至水面的必要性。当前，AUV在水下的通信受限，需要浮出水面进行高速、实时的通信，但这样易被雷达探测而导致隐蔽性降低。对于南海典型的不完整声道声速剖面^[10]而言，声速曲线呈现负梯度，近水面空间存在声影区，隐蔽性好，具有较高的战略意义。因此，本文拟提出一种利用折叠天线的AUV通信模式，即基于通信作业隐蔽性的需求，AUV运行至近水面空间后伸出折叠天线并露出水面，然后实现高速、实时的电磁波通信。为了保证通信的稳定性，需要保持天线与波浪表面间的恒定距离，也需要保持AUV本体与波浪表面间的恒定距离，即控制AUV在近水面空间完成波浪跟随运动。

折叠天线在AUV平台上的应用已经有较为成熟的研究结果^[11-12]。郑志航等^[11]设计了一种安装于AUV背部凹槽内的折叠天线机构并进行样机试验，验证了其水密性；Loni等^[13]对浮式单极天线展开了研究，该天线通过绝缘电线与水面下1 m处的封闭式传感器连接，在浅水域能达到30 m的信号传输距离，研究结果验证了穿透水面进行通信的天线系统的可行性。

AUV的运动自由度多且非线性效应突出，自动控制方法以PID控制为主。温秉权^[14]设计了航速、航向、纵倾和深度PID控制器，并在AUV模型样机试验中展现出了较好的鲁棒性，但应用场景局限于浅水域。Javanfar等^[15]针对波浪干扰下的潜望镜轨迹跟踪控制问题，设计了自适应PID控制器，该控制器对于工况点时变的系统具有较好的控制效果，但未将其直接应用于AUV的控制问题中。胡坤等^[16]设计了一种基于粒子群算法的潜艇定深非线性PID控制器，仿真结果表明，该控制器的稳态精度更好，舵机损耗更低。杜亮等^[17]研究了模型预测控制方法在航行器近水面运动控制中的应用，定深控制仿真实验显示，稳定性较好。文献[16-17]的研究仅建立了航行器垂直面运动模型，缺乏对航向控制的应用。袁昌斌等^[18]提出了一种基于滑膜变结构控制的AUV速度、航向控制器，仿真结果表明，在波浪作用下其对于航向也有较好的控制效果，但仅考虑了低海况情况，较高海况下的控制效果未知。Le等^[19]提出了一种基于模糊逻辑控制与线性控制相结合的舵控制器，相比传统的PID控制器，该控制器更适应环境扰动大的工况，但仅在三自由度的船舶运动问题上进行了仿真。Shojaei^[20]设计了一种基于神经网络的控制器，并对在环境干扰下的水下航行器进行仿真研究，结果表明，其有效降低了最大输入力矩，但这种方法较为依赖针对特定平台的数据集，迁移应用的效果较差。

AUV近水面运动操纵控制包括2个基本难点：一是需要通过试验或者流体力学理论获得现实海况对AUV的干扰力和干扰力矩，从而建立波浪作用下的操纵运动方程；二是需要基于特定的AUV平台，针对少于运动自由度的控制面来实现高精度的欠驱动控制，从而实现多自由度的控制。

综上，本文针对AUV在近水面空间进行通信作业的控制目标，通过切片理论进行规则波的波浪干扰力预报，将建立AUV的五自由度近水面运动方程，并结合视线法（line of sight，LOS）和PID控制器实现对AUV姿态及航速的控制，验证AUV在近水面空间进行波浪跟随运动的可行性，为高隐蔽、实时的通信提供理论模型支撑。

1.   通信作业流程

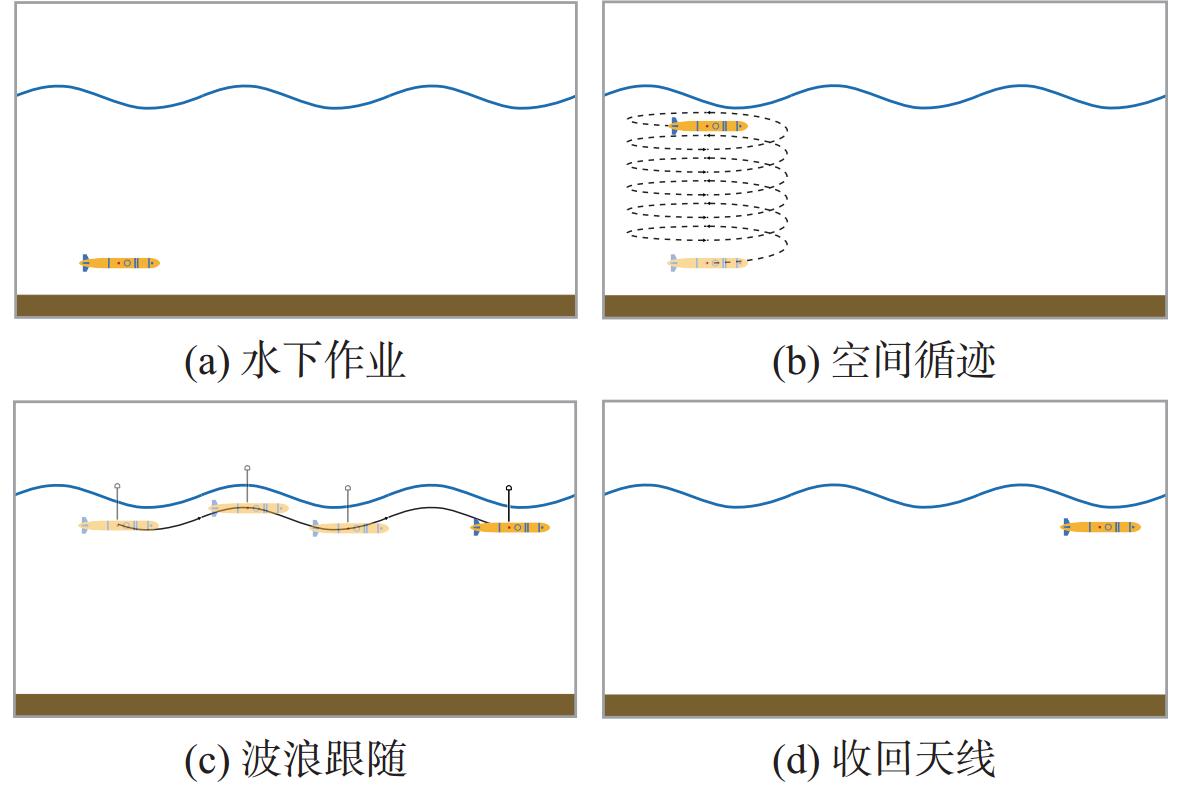
针对AUV现有通信手段不足的问题，提出一种带折叠天线近水面运动的通信作业流程。该通信作业流程分为4个部分，分别为水下作业、空间循迹、波浪跟随和收回天线，如图1所示（实际的波浪表面是时变的，图1做了简化处理）。

图  1  AUV通信作业流程示意图

Figure  1.  AUV communication operation process

下载: 全尺寸图片 幻灯片

1） 水下作业：AUV在水下一定深度进行指定作业。

2） 空间循迹：AUV沿规划的航迹进行空间循迹运动，然后上浮至近水面空间指定位置（声影区），距离水面一定的距离。

3） 波浪跟随：AUV伸出折叠天线使其露出水面，同时，AUV保持波浪跟随运动，并始终与水面保持一定的距离，实现实时通信。

4） 收回天线：AUV完成通信作业，收回折叠天线，然后根据实际任务需要在近水面空间待机或是下潜。

2.   规则波作用下AUV运动建模

2.1   规则波模型

本文考虑AUV在规则波中的运动，根据其在地球坐标系下的位置$(x,y)$、波频$\omega$、时间t和浪向角$\alpha$（波浪方向与地球坐标系$\xi$轴正方向的夹角），可以得到规则波的实时波面高度$\zeta (t)$^[21]为

式中：${\zeta _{\text{a}}}$为波幅，${\zeta _{\text{a}}}{\text{ = }}\dfrac{1}{2}H$，其中H为波高；速度势函数$\varPhi (x,y,t,\alpha ) =$ $\omega t - kx\cos \alpha - ky\sin \alpha$。

由势流理论可知，波浪方程需要满足运动学条件和动力学条件。规则波的速度势$\phi$为

式中：${\text{Re}}$为取实部运算；g为重力加速度；$\text{ }h$为水深；$(x,y,{\textit{z}})$为地球坐标系下的位置坐标；k为波数，满足色散关系${\omega ^2}/g = \tanh kh$。

规则波内部水粒子的运动幅度随深度z的增加而衰减。通过速度势，得到水粒子垂向位移${\zeta _{\text{3}}}$（向上为正）、垂向速度$w_{\text{water}}$、垂向加速度${a_{\text{3}}}$、水平位移${\zeta _{\text{1}}}$、水平速度$u_{\text{water}}$、水平加速度${a_{\text{1}}}$和压强${P_{\text{D}}}$分别为：

式中，$\rho$为海水密度。

2.2   五自由度运动模型

本文考虑近水面迎浪工况，AUV因横摇较小可忽略不计^[22]，将主要研究其在垂直面和水平面内的运动，包括纵荡、横荡、垂荡、纵摇和艏摇5个自由度。在随体坐标系中，将AUV的浮心作为原点。考虑到AUV的对称性，可以忽略绕重心的交叉转动惯量并认为侧向重心坐标${y_{\text{G}}} = 0$。此时，五自由度运动方程^[23]为

式中：m为AUV的质量；$u,v,w$分别为AUV的纵向速度、横向速度和垂向速度；$\dot u,\dot v,\dot w$分别为AUV的纵向加速度、横向加速度和垂向加速度；$q,r$分别为AUV的纵倾角速度和航向角速度；$\dot q,\dot r$分别为AUV的纵倾角加速度和航向角加速度；$({x_{\text{G}}},{{\textit{z}}_{\text{G}}})$为重心在随体坐标系下的坐标；${I_{{yy}}},{I_{{{\textit{z}}{\textit{z}}}}}$为转动惯量；$\sum X,\sum Y,\sum Z,\sum M,\sum N$为AUV在各自由度上所受的合外力，包括重力、浮力、舵力、推进器推力、水动力、波浪干扰力和力矩。

将式（10）展开整理为矩阵方程形式：

式中：${X_{\dot u}},{Y_{\dot v}},{Y_{\dot r}},{Z_{\dot w}},{Z_{\dot q}},{M_{\dot w}},{M_{\dot q}},{N_{\dot v}},{N_{\dot r}}$为水动力导数；${X_{{\text{vis}}}},{Y_{{\text{vis}}}},{Z_{{\text{vis}}}},{M_{{\text{vis}}}},{N_{{\text{vis}}}}$为非惯性水动力；${X_0}$为推进器推力；${Z_0}$为零升力；${M_0}$为零升力矩； ${Z_{{\delta _{\text{e}}}}},{M_{{\delta _{\text{e}}}}}$为水平舵角导数；${Y}_{{\delta }_{\text{r}}}，{N}_{{\delta }_{\text{r}}}$为垂直舵角导数；${\delta _{\text{e}}}$为水平舵角；${\delta _{\text{r}}}$为垂直舵角； ${X_{{\text{wave}}}},{Y_{{\text{wave}}}},{Z_{{\text{wave}}}},{M_{{\text{wave}}}},{N_{{\text{wave}}}}$为波浪干扰力和力矩。

本文在研究规则波对于AUV产生的波浪干扰力和力矩时沿用Froude−Krylov假设：1）波浪干扰力和力矩仅由流体压力引起；2）AUV在流体中产生的压力场不影响波浪的波场分布；3）波浪对AUV的干扰力和力矩是由水面下流体的压力场分布波动所引起。

切片理论^[24]适用于瘦削型航行器的波浪干扰力计算。假定航行器由许多直径不等的切片组成，每个切片都是无限长柱体的横剖面，则可以通过二维绕流理论来确定该剖面所受的波浪干扰力，然后沿航行器轴向积分得到波浪干扰力。规则波作用下的波浪干扰力以线性惯性力为主^[11]，所以在计算波浪干扰力和力矩时，本文主要考虑线性惯性力，则AUV单位长度的切片所受垂向波浪干扰力${\text{d}}{F_{{z}}}$的表达式为

式中：${K_{{\text{M3}}}}(l) = \rho {\text{π}}{C_{\text{M}}}{D^2}(l)/4$，其中${K_{{\text{M3}}}}(l)$为切片的垂向附加质量，$D(l)$为AUV关于轴向长度l的直径函数，${C_{\text{M}}}$为Keulegan−Carpenter数，取${C_{\text{M}}} = 2$^[20]；${a_3}(l)$由式（5）可得${a_3}(l) = - {\omega ^2}{\zeta _{\text{a}}}{\text{sin}}(\varPhi + kl\cos \alpha )\cdot \sinh k\left( { - {\textit{z}} + h} \right)/\sinh kh$。

对式（12）沿AUV轴向长度方向积分，考虑向下方向为正，则波浪垂向干扰力${Z_{{\text{wave}}}}(t)$为

式中：${A}_{3}\left({\textit{z}}\right)=-{\omega }^{2}{\zeta }_{\text{a}}\mathrm{sinh}k\left(-{\textit{z}}+h\right)/\mathrm{sinh}kh$；$L$为AUV的长度。

考虑各切片到AUV浮心的轴向距离，则纵倾干扰力矩${M_{{\text{wave}}}}\left( t \right)$为

AUV所受波浪侧向干扰力${Y_{{\text{wave}}}}\left( t \right)$和偏航干扰力矩${N_{{\text{wave}}}}\left( t \right)$为

式中：${A_{\text{1}}}\left( {\textit{z}} \right)$由式（8）定义，有${A_{\text{1}}}\left( {\textit{z}} \right) = {\omega ^2}{\zeta _{\text{a}}}\cosh k( - {\textit{z}} + h )/\sinh kh$；因AUV的横截面近似为圆形，故有${{K}_{{\text{M2}}}}\left( l \right) = {{K}_{{\text{M3}}}}\left( l \right) = \rho {\text{π}}{C_{\text{M}}}{{D}^2}\left( l \right)/4$。

计算AUV所受的波浪轴向干扰力时，可以近似考虑直径为AUV最大直径的水平圆柱体。由式（9）可得前、后表面所受轴向压力差即为轴向干扰力${X_{{\text{wave}}}}\left( t \right)$：

3.   AUV控制算法

3.1   LOS算法

LOS是受舵手操舵启发的一种航迹跟踪控制算法^[25-26]。该算法的原理是：通过控制，使AUV的俯仰角$\theta$和航向角$\psi$与时变的视线角保持一致，在此过程中，AUV即可沿规划的航迹运动，完成航迹跟踪。针对本文的AUV欠驱动控制，LOS能够将控制量从五自由度的AUV位置$\left( {x,y,{\textit{z}}} \right)$和AUV姿态角$\left( {\theta ,\psi } \right)$减少到三自由度的AUV俯仰角$\theta$、航向角$\psi$和纵向速度u。

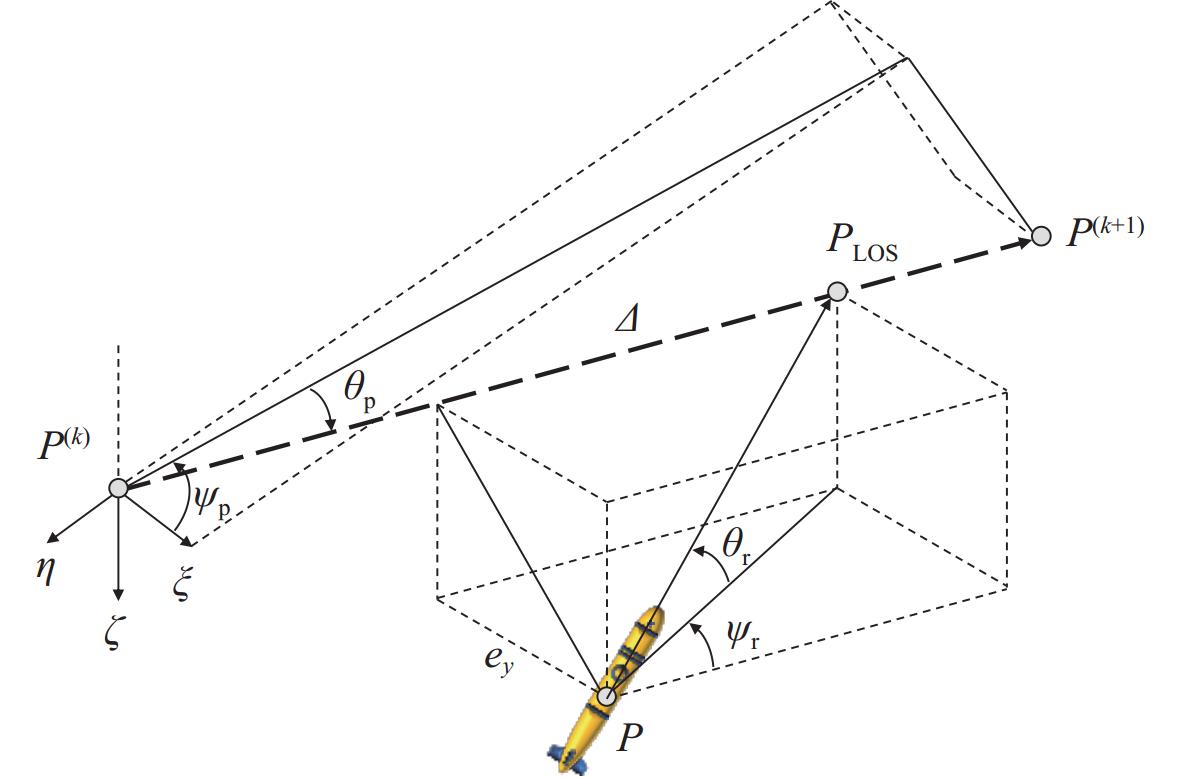
假设AUV的实际位置为${\boldsymbol{P}} = {\left[ {x,y,{\textit{z}}} \right]^{\text{T}}}$，AUV上一步的规划位置为${{\boldsymbol{P}}^{\left( k \right)}} =$${\left[ {{x^{\left( k \right)}},{y^{\left( k \right)}},{{\textit{z}}^{\left( k \right)}}} \right]^{\text{T}}}$，AUV下一步的规划位置为${{\boldsymbol{P}}^{\left( {k + 1} \right)}} = {\left[ {{x^{\left( {k + 1} \right)}},{y^{\left( {k + 1} \right)}},{{\textit{z}}^{\left( {k + 1} \right)}}} \right]^{\text{T}}}$，则规划航迹的方向角${\theta _{\text{p}}}$和${\psi _{\text{p}}}$为：

由图2（其中$(\xi , \eta , \zeta )$为地球坐标系）所示，从AUV的实际位置P向规划航迹投影，可得横向偏差${e_y}$和垂向偏差${e_{\textit{z}}}$。为了消除偏差，选取$\overrightarrow {{P^{\left( k \right)}}{P^{\left( {k + 1} \right)}}}$上一点${{\boldsymbol{P}}_{{\text{LOS}}}}$作为目标点，$\boldsymbol{P}_{\text{LOS}}$与P在规划航迹上投影的距离$\varDelta = cL$（ 其中$c = 2～5$）^[27]，可得AUV实际位置P到目标点${P_{{\text{LOS}}}}$的方向角${\theta _{\text{r}}}$和${\psi _{\text{r}}}$为：

图  2  AUV的LOS航迹跟踪示意图

Figure  2.  Schematic diagram of AUV LOS track following

下载: 全尺寸图片 幻灯片

则通过LOS输出的视线角${\theta _{{\text{LOS}}}}$和${\psi _{{\text{LOS}}}}$为：

将视线角${\theta _{{\text{LOS}}}}$作为指令俯仰角，${\psi _{{\text{LOS}}}}$作为指令航向角，则指令航速${u_{\text{d}}}$由规划航迹及航行总时长计算得出。

3.2   基于LOS的PID控制

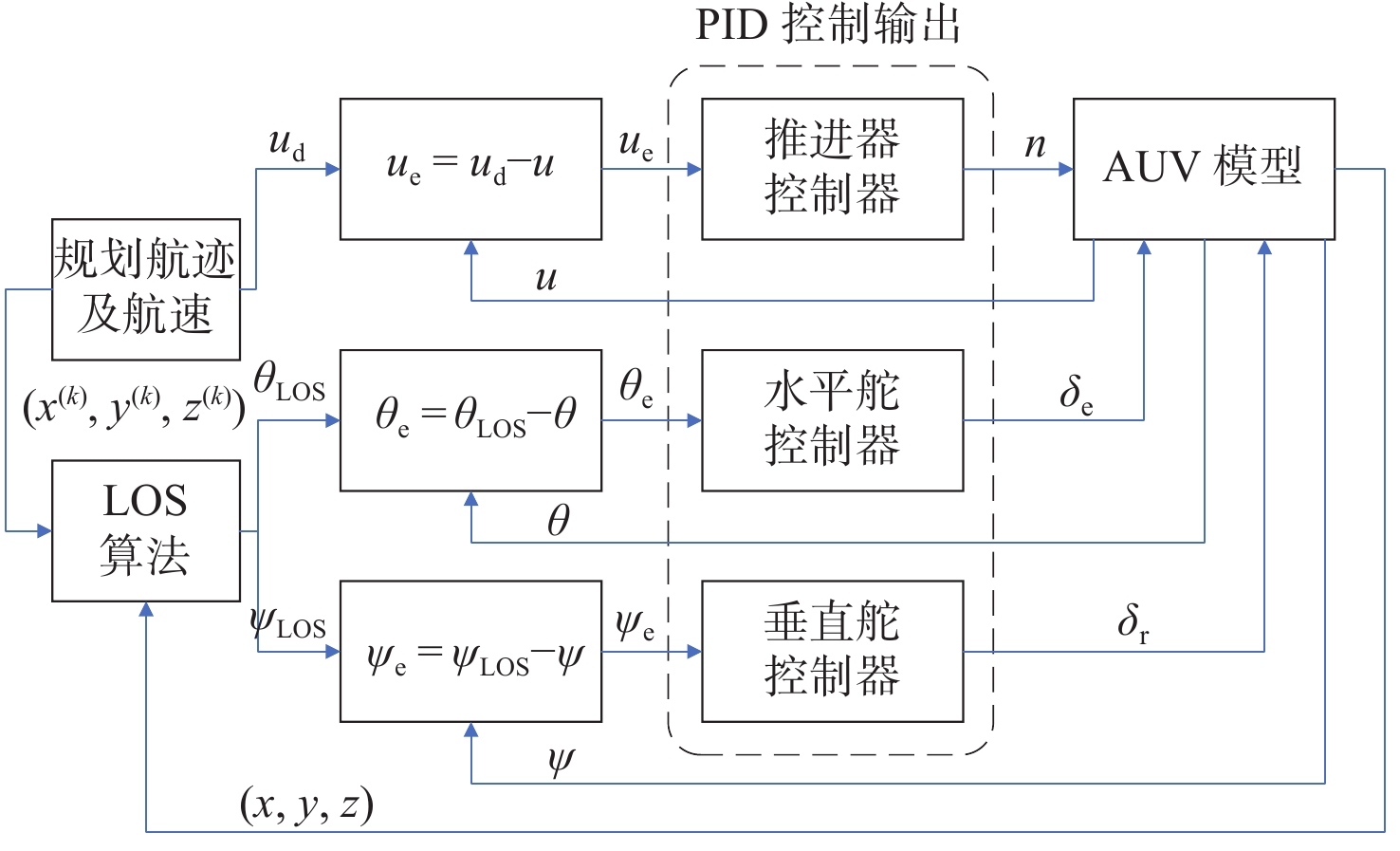
为了使AUV的俯仰偏差角${\theta _{\text{e}}}$和航向偏差角${\psi _{\text{e}}}$趋于0，俯仰角$\theta$和航向角$\psi$趋于指令俯仰角${\theta _{{\text{LOS}}}}$和指令航向角${\psi _{{\text{LOS}}}}$，航行速度偏差${u_{\text{e}}}$趋于0，u趋于指令航速${u_{\text{d}}}$，因此本文采用PID控制，控制示意图如图3所示。

图  3  PID控制系统原理图

Figure  3.  Block diagram of PID control system for AUV

下载: 全尺寸图片 幻灯片

由图3可知，通过设定合理的PID控制器参数，便可得到稳定的控制输出，使控制偏差趋于0。PID控制器的控制规律为：

式中：${n^{\left( {k + 1} \right)}},\delta _{\text{e}}^{\left( {k + 1} \right)},\delta _{\text{r}}^{\left( {k + 1} \right)}$分别为第$k + 1$步输出的推进器转速、水平舵角和垂直舵角；${k_{{u{\rm{p}}}}},{k_{{u{\rm{d}}}}},{k_{{u{\rm{i}}}}}, {k_{\theta{\text{p}}}}, {k_{\theta{\text{d}}}}, {k_{\theta{\text{i}}}},{k_{\psi {\text{p}}}},{k_{\psi {\text{d}}}}, {k_{\psi {\text{i}}}}$为PID控制器参数；$u_{\text{e}}^{\left( {k + 1} \right)},\theta _{\text{e}}^{\left( {k + 1} \right)},\psi _{\text{e}}^{\left( {k + 1} \right)}$分别为第$k + 1$步的航行速度偏差、俯仰偏差角和航向偏差角。

由式（24）～式（26）可知，当出现较大偏差时，PID控制输出也随之增大，达到调节控制目标的目的。只要偏差存在，则PID控制输出同样存在，直到控制偏差值为0。

4.   仿真结果及分析

为证明上述规则波模型及控制策略的有效性，基于实际应用需求开展仿真模拟。将REMUS AUV作为仿真研究对象，主要参数如下： 总长$L = 1.33{\text{ m}}$，最大直径$d = 0.19{\text{ m}}$，重量$m = 30.39{\text{ kg}}$，排水量$\nabla = 0.031\;5 {{\text{ m}}^{\text{3}}}$，轮廓函数$D(x)$由文献[28]给出。仿真过程包括空间循迹运动和波浪跟随运动。其中，空间循迹运动要求AUV从水下释放，沿螺旋型航迹抵达近水面空间；波浪跟随运动则要求AUV在近水面空间以稳定速度航行，并与波面保持设定距离${h_{\text{d}}} = 1 {\text{ m}}$。

从初始位置（0 m，0 m，−50 m）释放REMUS AUV，设定航迹点位1（0 m，0 m，−37.75 m）、点位2（0 m，0 m，−25.5 m）、点位3（0 m，0 m，−13.25 m）和点位4（0 m，0 m，−1 m），然后沿如下规划航迹进行空间循迹运动：

AUV航行至（0 m，0 m，−1 m）后，开始执行通信任务，然后沿如下航迹进行波浪跟随运动：

仿真实验的各参数设计如下。

1） 规则波模型参数：水深h = 100 m，波浪周期T = 10 s，浪向角α = 180º，波高H = 1 m。

2） PID控制器参数：${k}_{u{\rm{p}}}=1.5,{k}_{u{\rm{d}}}=0.5$, ${k}_{u{\rm{i}}}=0.1, {k}_{\theta \text{p}}=3.5,{k}_{\theta \text{d}}=0.8$, ${k}_{\theta \text{i}}=0.3,{k}_{\psi \text{p}}=0.4,{k}_{\psi \text{d}}=0.3,{k}_{\psi \text{i}}=0$。

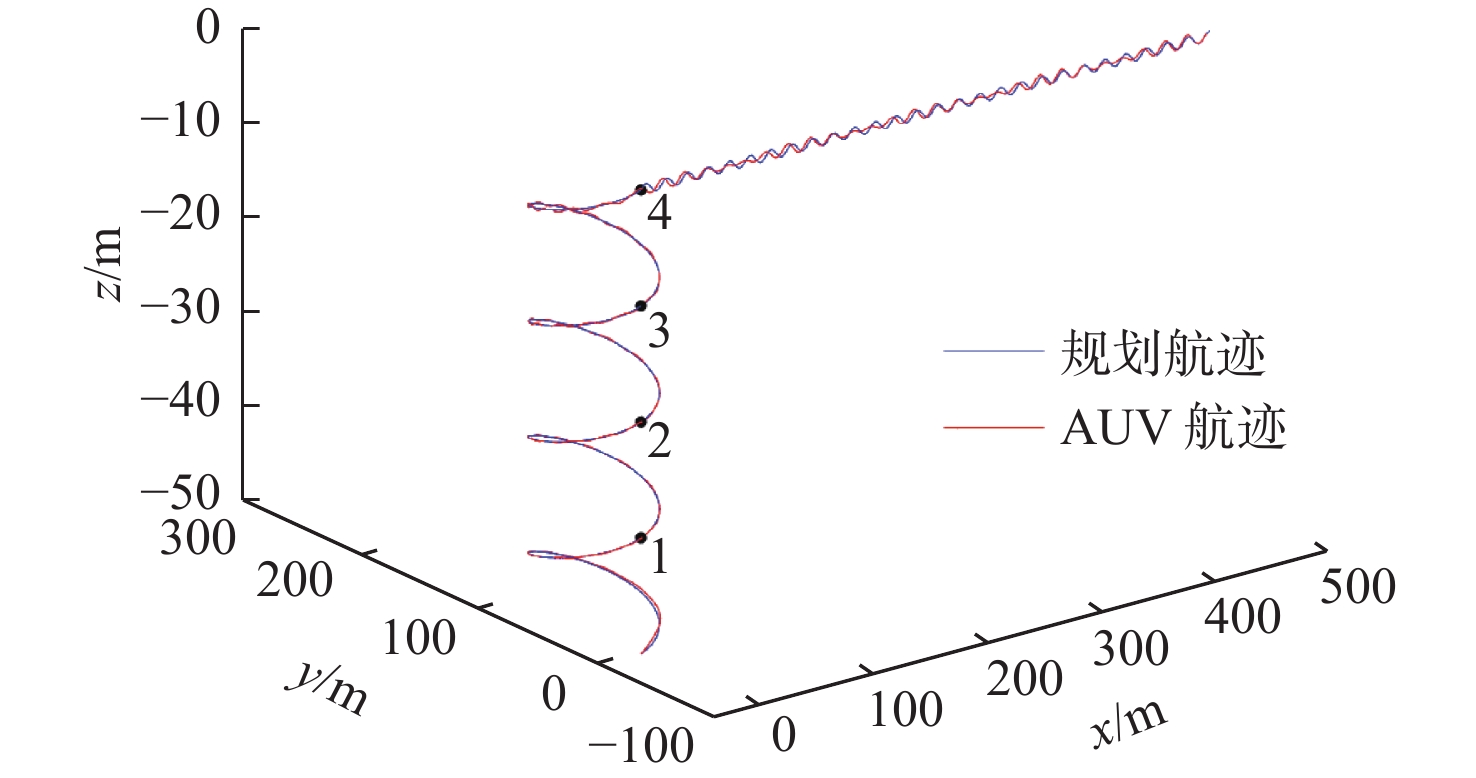
仿真结果如图4～图8所示。其中，图4所示为包括空间循迹运动和波浪跟随运动的航迹跟踪曲线，图5所示为空间循迹运动时变曲线。由图4可知，AUV的实际航迹与规划航迹基本吻合，表明其能够较好地进行空间循迹运动，以及通过LOS算法实现航迹跟踪。由图5可知，纵向和横向的循迹运动整体趋势与规划航迹基本一致，但在时间上存在一定的滞后性，仍有较大的改进空间。垂向的循迹运动一开始吻合较好，但在运动后段出现了振荡现象，离水面越近，振荡幅度越大，垂向的跟踪偏差最大为0.550 1 m，这是因为近水面空间受到波浪干扰力和干扰力矩的影响更大，表明仿真能够较好地反映波浪在近水面空间对AUV的影响。

图  4  航迹跟踪曲线

Figure  4.  Track following curves

下载: 全尺寸图片 幻灯片

图  5  空间循迹运动时变曲线

Figure  5.  Time domain curves of spatial tracking motion

下载: 全尺寸图片 幻灯片

图  6  波浪跟随运动PID控制

Figure  6.  Wave following motion PID control

下载: 全尺寸图片 幻灯片

图  7  波浪跟随运动垂向位置时变曲线

Figure  7.  Time domain curves of the vertical position of wave following motion

下载: 全尺寸图片 幻灯片

表1所示为AUV在空间循迹运动中实际航迹点与对应点位的跟踪误差。由表可知，在空间循迹运动中，4个航迹点位的跟踪偏差均小于0.25倍艇长。航迹跟踪的控制效果可通过指定方向上的跟踪精度，即实际航迹与规划航迹坐标的均方根差（root mean square error，RMSE）来评估。以点位1～4的航迹作为考核段，其最大纵向跟踪偏差为5.043 0 m，最大法向跟踪偏差为0.963 7 m，法向跟踪稳定精度为0.247 6 m，这表明基于LOS的PID控制算法虽然具备一定的滞后性，但对于AUV而言，纵向跟踪偏差和法向跟踪偏差这2项性能指标均满足工程使用要求^[29]。

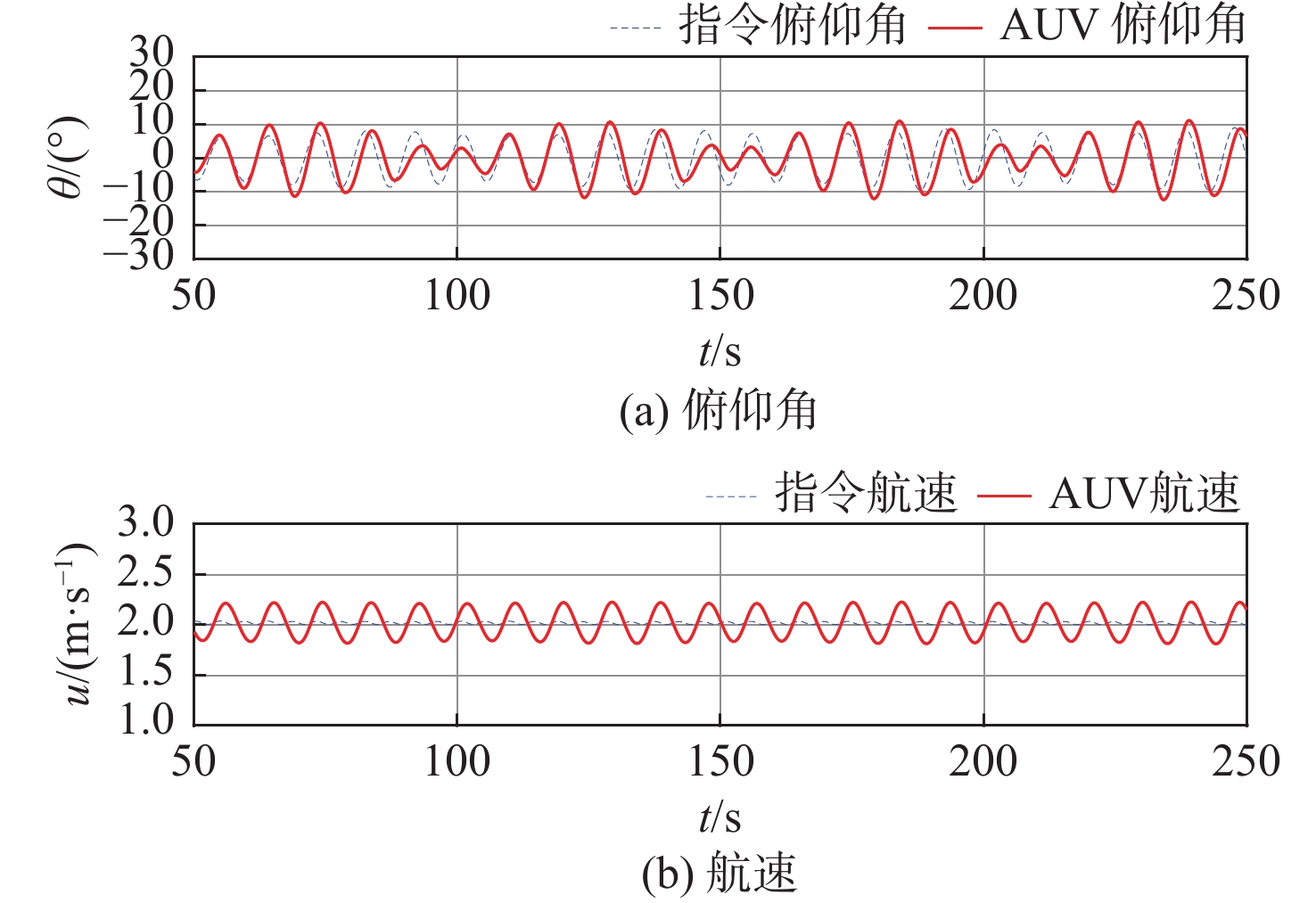
表  1  航迹点跟踪偏差

Table  1.  Tracking deviation of track point

点位序号	实际航迹点			跟踪偏差/m
	x/m	y/m	z/m
1	−0.081	−0.307	−37.771	0.318
2	0.052	−0.211	−25.475	0.218
3	0.060	−0.177	−13.286	0.190
4	−0.034	−0.240	−0.792	0.320

下载: 导出CSV 

| 显示表格

图6所示为波浪跟随运动PID控制下的俯仰角和航速时变曲线。由图可知，在波浪跟随运动中，采用LOS算法能够有效输出时变的指令俯仰角和指令航速。当俯仰角$\theta$在0°附近振荡时，最大绝对值小于12°。当航速在2 m/s附近振荡时，偏差的最大绝对值小于0.2 m/s。指令俯仰角、指令航速的变化相位与AUV的实际俯仰角和航速的变化相位一致，表明其对应的PID控制器起到了较好的控制效果。

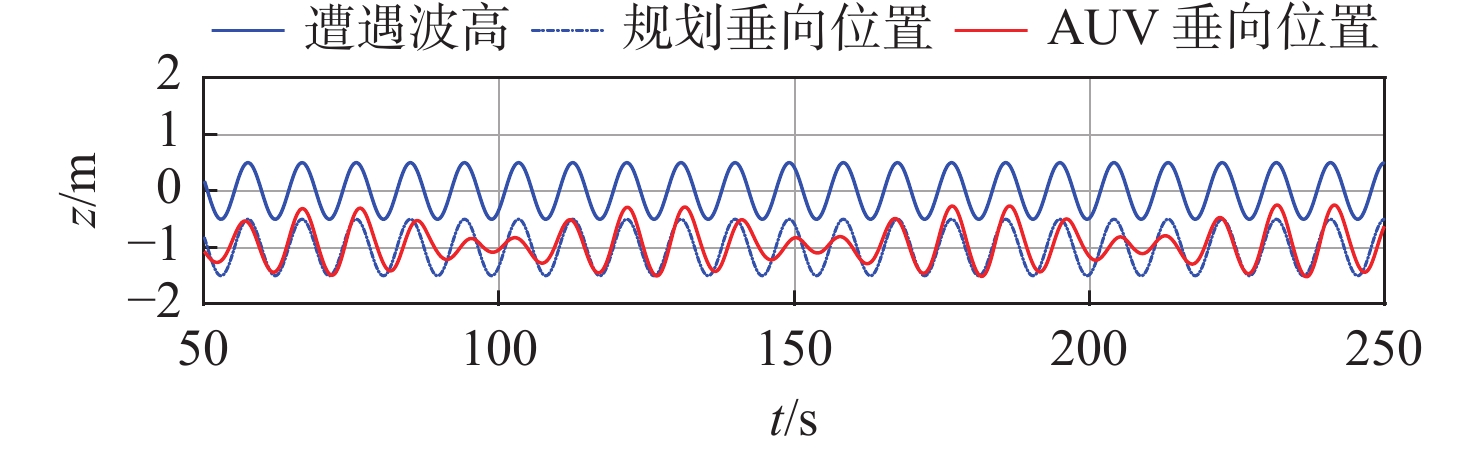
图7所示为波浪跟随运动垂向位置时变曲线。由图可知，AUV的垂向位置与遭遇波高的垂向位置差h在设定距离${h_{\mathrm{d}}}$的附近振荡，垂向跟踪偏差最大为0.483 6 m，垂向跟踪稳定精度为0.232 6 m，表明基于切片理论的波浪干扰力计算方法可行，基于LOS的PID控制算法能够满足波浪跟随的控制要求，但只能保持波浪跟随运动航迹的相位与遭遇波高一致，而垂向位置差h的波动则较大，这是因为近水面的波浪干扰力或干扰力矩过大，AUV的舵所产生的水动力有限。

图8展示了152～174 s时间内波浪跟随运动控制效果。由图可见，在算法控制下，AUV的垂向位置随遭遇波高的变化而变化，基本保持与遭遇波高相距${h_{\text{d}}} = 1\; {\text{m}}$；同时，AUV以约2 m/s的航行速度在纵向方向上前进，自身姿态角未发生过大变化，具备完成通信任务的基本能力。

图  8  波浪跟随控制效果（T = 152～174 s）

Figure  8.  Wave following control effect (T = 152～174 s)

下载: 全尺寸图片 幻灯片

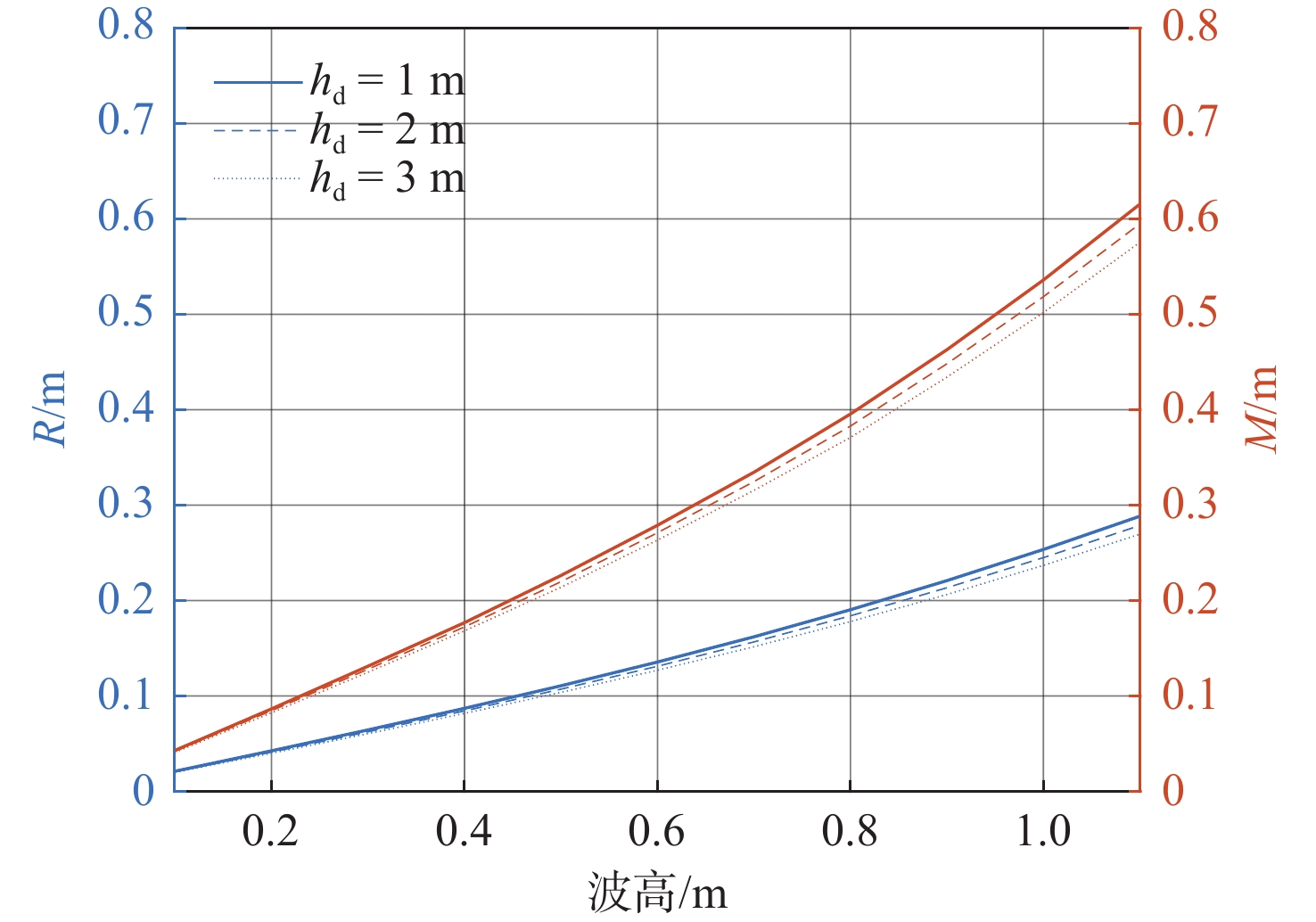
图9所示为波频为0.628 3 rad/s时，不同波高规则波下AUV在波浪跟随运动中相对遭遇波高的垂向位置差h的均方根误差R及最大偏差M（$M{\text{ = }}{\left| {h - {h_{\text{d}}}} \right|_{{\text{max}}}}$），具体数据如表2所示。

图  9  波高对波浪跟随控制效果的影响

Figure  9.  The influence of wave height on wave following control effect

下载: 全尺寸图片 幻灯片

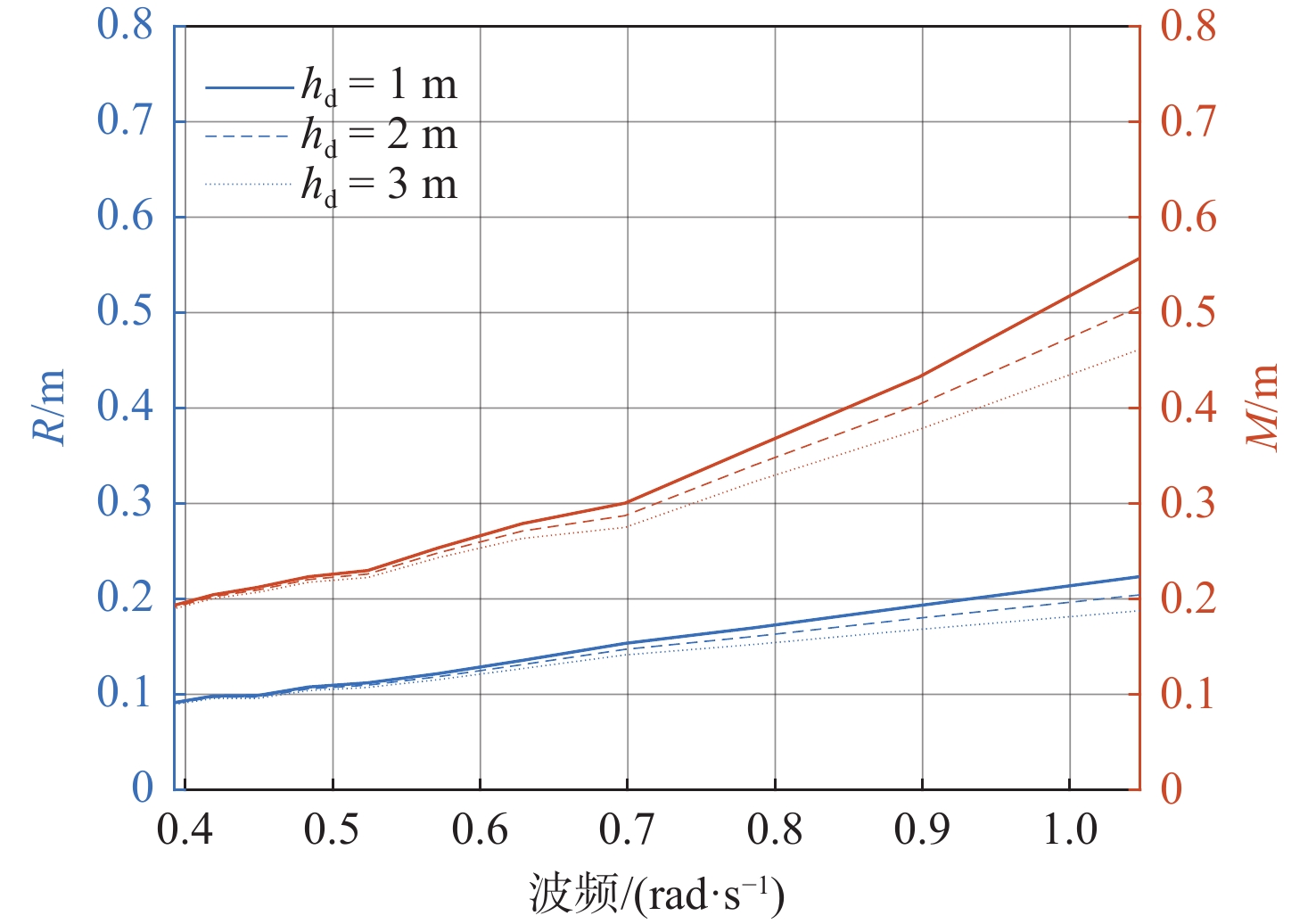
表  2  波高分析

Table  2.  Wave height analysis

波高/m	${h_{\text{d}}} = 1 {\text{ m}}$			${h_{\text{d}}} = 2 {\text{ m}}$			${h_{\text{d}}} = 3 {\text{ m}}$
	R/m	M/m		R/m	M/m		R/m	M/m
0.1	0.021	0.043		0.020	0.042		0.020	0.041
0.2	0.043	0.086		0.041	0.085		0.040	0.082
0.3	0.064	0.131		0.062	0.128		0.060	0.125
0.4	0.087	0.177		0.084	0.172		0.082	0.168
0.5	0.111	0.226		0.107	0.220		0.104	0.214
0.6	0.136	0.279		0.131	0.271		0.127	0.263
0.7	0.162	0.335		0.157	0.325		0.152	0.316
0.8	0.190	0.396		0.184	0.383		0.178	0.371
0.9	0.221	0.463		0.213	0.448		0.206	0.434
1.0	0.254	0.536		0.245	0.519		0.237	0.502

下载: 导出CSV 

| 显示表格

图10所示为波高为0.3 m时，不同波频规则波下AUV在波浪跟随运动中相对遭遇波高的垂向位置差h的均方根误差R及最大偏差M（$M= {\left| {h - {h_{\text{d}}}} \right|_{{\text{max}}}}$），具体数据如表3所示。

图  10  波频对波浪跟随控制效果的影响

Figure  10.  The influence of wave frequency on wave following control effect

下载: 全尺寸图片 幻灯片

表  3  波频分析

Table  3.  Wave frequency analysis

波频/（rad∙s−1）	${h_{\text{d}}} = 1 {\text{ m}}$			${h_{\text{d}}} = 2 {\text{ m}}$			${h_{\text{d}}} = 3 {\text{ m}}$
	R/m	M/m		R/m	M/m		R/m	M/m
0.419	0.098	0.204		0.097	0.202		0.096	0.200
0.449	0.099	0.212		0.097	0.209		0.096	0.207
0.483	0.108	0.223		0.106	0.220		0.104	0.217
0.524	0.112	0.230		0.110	0.226		0.107	0.222
0.571	0.122	0.253		0.118	0.248		0.115	0.243
0.628	0.136	0.279		0.131	0.271		0.127	0.263
0.698	0.153	0.300		0.147	0.287		0.141	0.275
0.785	0.170	0.359		0.161	0.340		0.152	0.323
0.898	0.193	0.433		0.180	0.404		0.168	0.378
1.047	0.223	0.557		0.204	0.506		0.188	0.462

下载: 导出CSV 

| 显示表格

由图表可知，随着波高和波频的增大，控制效果随之变差，这是因为波浪干扰力和干扰力矩变大，作用在AUV上的合外力也会变大；随着设定距离${h_{\rm{d}}}$增大，控制效果会变好，这是因为离水面越远，波浪对AUV的影响将更小；波高对于控制效果的影响更加显著。

5.   结　论

本文提出了一种能够实现高隐蔽实时通信的AUV近水面通信模式，并针对该通信模式的控制目标，研究了AUV在近水面空间进行空间循迹及波浪跟随运动的建模与控制方法。随后，根据势流理论的规则波模型，运用切片理论计算了波浪干扰力和干扰力矩，建立了AUV的五自由度运动模型，使用基于LOS的PID控制实现了近水面的波浪跟随控制并进行了仿真实验。主要得到如下结论：

1） 势流理论的规则波模型及切片理论能够较好地反映近水面空间波浪对AUV的影响；

2） 基于LOS的PID控制算法能够较好地实现空间循迹控制，并满足波浪跟随的控制需要；

3） 增大波高和波频会降低控制效果，对AUV的机动性将要求更高。

后续，可以考虑不规则波干扰下的波浪跟随运动控制，以更贴合实际应用场景；同时，也可以改进控制器，考虑自适应PID控制和模型预测控制等更为先进的控制理论进行研究。