0.   引　言

面对多样化的任务需求以及海洋环境的复杂多变，单艘无人水面艇（USV）在执行任务时不可避免地会存在承载能力小、执行效率低、容错能力差等缺陷。随着协同控制技术的发展，多艘USV协同工作逐渐成为一种弥补单艘USV上述缺陷的有效解决方案。协同运动控制技术作为多艇协同系统的关键技术，也受到了国内外研究人员的广泛关注^[1-3]。

协同路径跟踪是多艇协同运动中的一种典型工作模式，其规定多艘USV以特定队形结构布局，并沿着预设路径航行。由于通信带宽的限制与传感器感知能力的不同，多艇协同运动控制结构可分为集中式、分布式与分散式。其中，分布式控制对运算能力要求不高，在计算资源受限、通信带宽窄的协同系统中具有较高的工程应用价值，并成为当下广泛应用的控制结构^[4]。作为一类非线性时变强耦合系统，USV航行时将受到海风、海浪与海流造成的时变外界环境干扰^[5]。与此同时，水动力参数摄动也会使得USV存在模型不确定动态^[6]。上述时变干扰会严重影响USV协同路径跟踪过程中的稳定性与可靠性。针对上述问题，现有抗扰控制方法的设计可根据处理层级的不同分为运动学抗扰设计与动力学抗扰设计。

协同路径跟踪控制系统通常可分为运动学控制子系统和动力学控制子系统。Fossen团队将运动学控制子系统的设计分解为位置跟踪设计与路径参数同步设计，通过构建运动学协同控制器实现路径跟踪和队形保持，开启了USV协同路径跟踪控制的先河^[7]。Borhaug和 Ghommam等^[8-9]考虑未知漂角问题，在漂角缓变的前提下分别采用积分器和自适应方法设计积分视线引导律和自适应视线引导律。Liu和Wang等^[10-11]设计了基于扩张状态观测器（extended state observer，ESO）的视线引导律。Gu等^[12]将视线引导律引入USV协同路径跟踪中，并利用降阶扩张状态观测器（reduced extended observer，RESO）处理漂角问题。然而，上述运动学控制子系统的设计均将USV状态直接作为输入，未考虑测量噪声的影响，且限制了漂角大小和变化速率。

动力学抗扰控制方法可分为被动抗干扰控制与主动抗干扰控制。被动抗干扰控制依靠自身算法的鲁棒性抑制干扰，常见方法有自适应控制^[13]、滑模控制^[14]、H∞鲁棒控制^[15]等。 Sun等^[14]针对协同系统存在未知参数和环境干扰问题，利用自适应理论分别设计参数估计器和上界估计器，消除模型不确定和环境扰动影响。Wang等^[16]根据自适应终端滑模设计有限时间动力学控制器，显著提升了系统平衡点的收敛速度。主动抗干扰控制方法则是通过逼近器或观测器估计出未知干扰，并将其作为补偿项引入到反馈控制器中。Peng等^[17]利用神经网络设计自适应神经网络估计器，在线估计系统中的未知动态与环境干扰。Qu等^[18]则采用模糊估计理论，设计基于预测的模糊状态观测器以消除系统未知动态和洋流干扰。Zhang等^[19]针对USV状态不可测以及未知动态和干扰的问题，提出一种基于线性ESO的干扰估计方法。随后，为提高控制系统的暂态性能，Yu和Chang等^[20-21]分别设计基于有限时间ESO与固定时间ESO的滑模控制器，有效减少了扰动估计时间。综上所述，被动抗干扰控制依靠自身算法的鲁棒性抑制干扰，适应性和灵活性有限。与此同时，空间限制与成本约束也使得多艘USV在协同运动过程中往往并未搭载速度传感器，因此基于全状态反馈的主动抗干扰控制也无法适用于该场景^[22]。基于ESO的输出反馈控制则能够同时处理未知干扰与速度不可测问题，因此在多艇协同路径跟踪领域得到了广泛应用。然而，现有研究并未考虑测量数据中包含的噪声，该高频干扰不仅会影响ESO的估计速度与精度，而且会造成后端执行机构的频繁响应。

基于以上分析，本文拟提出一种基于KFESO的多艇分布式协同路径跟踪复合抗扰控制方法，旨在解决高低频混合多源干扰问题。首先，联合Kalman滤波器构造KFESO，对输入进ESO中的数据进行最优滤波，同时应用ESO扩展项对低频扰动项进行估计。其次，设计分布式状态观测器观测虚拟领航艇速度信息，并根据参考速度估计值以及KFESO输出的位置和速度估计值，设计运动学协同控制器。在此基础上，基于状态与干扰估计值，利用反步法与动态面控制技术设计动力学抗扰控制器。然后，使用李雅普诺夫稳定性理论进行控制系统的稳定性分析。最后，通过仿真与对比分析验证所提方法的有效性。

相比于前述工作，本文所设计控制方法将具有如下优势：

1） 基于KFESO的状态估计方法可以实现从含有测量噪声的测量数据中精确且快速地估计出USV各阶状态量与集总扰动，相比于标准ESO，其能缓解估计速度与精度之间的矛盾。

2） 利用分布式状态观测器和协同控制律可以实现分布式控制结构，使得无人艇仅与邻居无人艇通信即可估计出虚拟领航艇参考速度。相比于集中式控制结构，其占用的通信资源和计算资源较低，可扩展性较高。

1.   预备知识与问题描述

1.1   图　论

一般利用拓扑图$\mathcal{G} = \left\{ {\mathcal{V},\mathcal{E}} \right\}$对信息传输关系进行描述。$V = \left\{ {{n_1},{n_2}, \ldots ,{n_N}} \right\}$为N艘USV构成的节点集合，${n_i}$表示第i艘USV（USVi）；$\mathcal{E} = \{ < {n_i},{n_j} > \} \subseteq {\mathcal{V}} \times {\mathcal{V}}$为边集合，边${\text{ < }}{n_i},{n_j}{\text{ > }}$表示${n_j}$可以获取${n_i}$的信息。若对于任意节点对${n_i}$与${n_j}$，${\text{ < }}{n_i},{n_j}{\text{ > }} \in \mathcal{E}$且${\text{ < }}{n_j},{n_i}{\text{ > }} \in \mathcal{E}$，则$\mathcal{G}$为无向图，否则为有向图。此外，若存在节点$\bar n$，对于任意其余节点${n_k}$，均有一条有向连续路径使得信息可以从$\bar n$传输至${n_k}$，则称$\mathcal{G}$存在一棵根节点为$\bar n$的生成树。邻接矩阵$\mathcal{A}{\text{ = [}}{a_{ij}}{\text{]}} \in {{\bf{R}}^{N \times N}}$反映USV间的数据传输关系，若${\text{ < }}{n_j},{n_i}{\text{ > }} \in \mathcal{E}$，则${a_{ij}} = 1$，否则${a_{ij}} = 0$。特殊情况下，$\mathcal{B}{\text{ = diag}}\left( {{b_{10}},{b_{20}}, \ldots ,{b_{N0}}} \right) \in {{\bf{R}}^{N \times N}}$，${b_{i0}}$表示虚拟领航艇${n_0}$与${n_i}$的数据传输关系，若${n_i}$可以获取${n_0}$的信息，则${b_{i0}} = 1$，否则${b_{i0}} = 0$。拉普拉斯矩阵$\mathcal{L} = \mathcal{D} - \mathcal{A}$，其中$\mathcal{D}{\text{ = diag}}\left( {{d_1},{d_2}, \ldots ,{d_N}} \right)$，${d_i} = \sum\nolimits_{j = 1}^N {{a_{ij}}}$。

1.2   相关引理

引理1^[23]：对于由N+1个节点构成的有向图G，若其包含一棵以节点${n_0}$为根节点的生成树，则存在正定矩阵${\boldsymbol{P}} \in {{\bf{R}}^{N \times N}}$和${\boldsymbol{Q}} \in {{\bf{R}}^{N \times N}}$，使得$Q =$ $P\left( {\mathcal{L} + \mathcal{B}} \right) + {\left( {\mathcal{L} + \mathcal{B}} \right)^{\text{T}}}{\boldsymbol{P}}$。其中，${\boldsymbol{P}} = {\text{diag}}( {{1 / {{p_1}}},} \ldots ,$ ${{1 / {{p_N}}}} )$，${p_i}$为向量${\left( {\mathcal{L} + \mathcal{B}} \right)^{ - 1}}{{\underline{1}} _N}$的第i个元素，${{\underline {1}} _N} = {[1,1, \ldots ,1]^{\text{T}}} \in {{\bf{R}}^{N \times 1}}$。

引理2^[24]：对于任意向量${\boldsymbol{x}},{\boldsymbol{y}} \in {{\bf{R}}^{N \times 1}}$，不等式（1）成立：

式中：$\varepsilon {\text{ > 0}}$为一正常量；$\Vert ·\Vert$为Euclidean范数；a>1，b>1均为正常量，且满足$\left( {a - 1} \right)\left( {b - 1} \right) = 1$。

1.3   USV数学模型

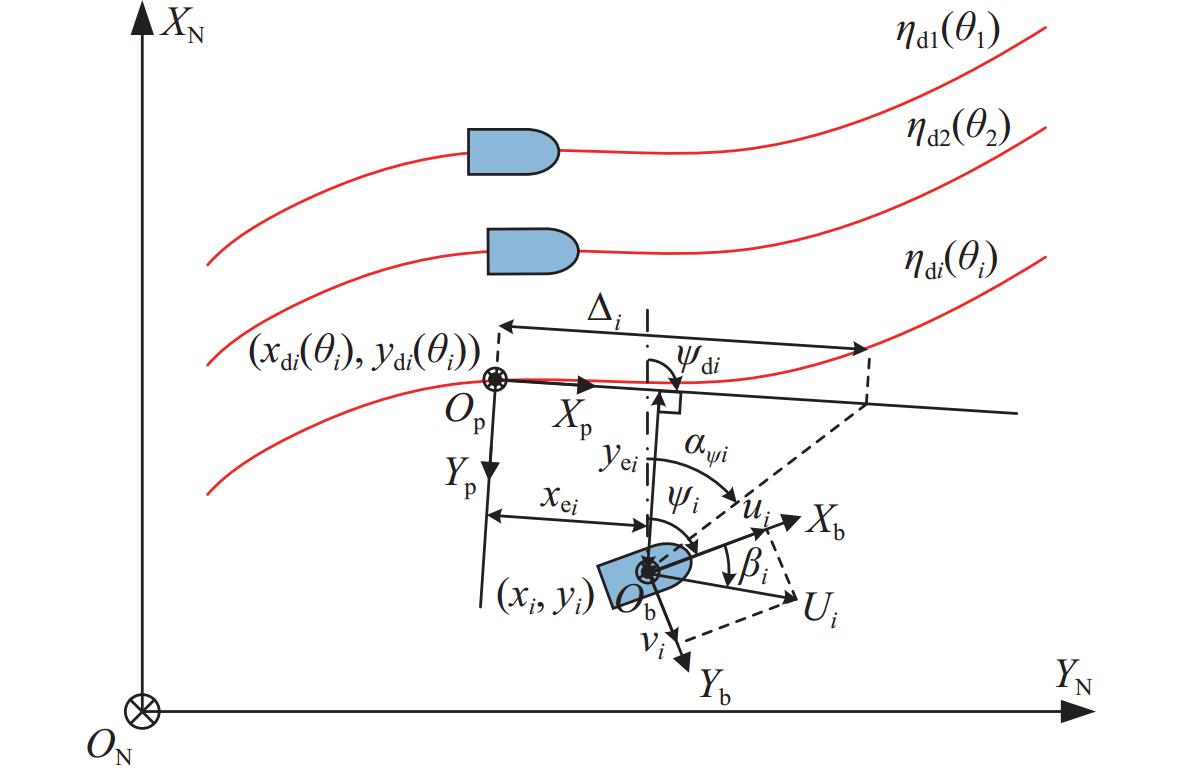
对于USV水面协同作业，现通常只考虑水平面三自由度运动。为便于描述USV运动状态，分别定义北东坐标系${O_{\text{N}}} - {X_{\text{N}}}{Y_{\text{N}}}{Z_{\text{N}}}$与附体坐标系${O_{\text{b}}} - {X_{\text{b}}}{Y_{\text{b}}}{Z_{\text{b}}}$，如图1所示。

图  1  参数化路径下的协同路径跟踪

Figure  1.  Coordinated path following under parameterized paths

下载: 全尺寸图片 幻灯片

考虑动力学模型不确定性、时变环境干扰以及测量噪声构成的高低频混合多源干扰，USVi水平面三自由度数学模型为

式中：${{\boldsymbol{\eta }}_i} = {[{x_i},{y_i},{\psi _i}]^{\text{T}}}$为北东坐标系下的位置和艏向角；${{\boldsymbol{\upsilon }}_i} = {[{u_i},{v_i},{r_i}]^{\text{T}}}$为附体坐标系下的线速度和角速度；${{\boldsymbol{\tau }}_i} = {[{\tau _{ui}},{\tau _{vi}},{\tau _{ri}}]^{\text{T}}}$为控制力（矩）；${{\boldsymbol{\tau }}_{{\text{E}}i}} = [{\tau _{{\text{E}}ui}},$ ${\tau _{{\text{E}}vi}},{\tau _{{\text{E}}ri}}{]^{\text{T}}}$为时变环境力（矩）；${{\boldsymbol{M}}_{0i}} \in {{\bf{R}}^{3 \times 3}}$，${{\boldsymbol{C}}_{0i}}({{\boldsymbol{\upsilon }}_i})$$\in {{\bf{R}}^{3 \times 3}}$与${{\boldsymbol{D}}_{0i}}({{\boldsymbol{\upsilon }}_i}) \in {{\bf{R}}^{3 \times 3}}$分别为系统惯性矩阵、科里奥利向心力矩阵与阻尼矩阵的标称值；$\varDelta {{\boldsymbol{\tau }}_i} =$ ${[\varDelta {\tau _{ui}},\varDelta {\tau _{vi}},\varDelta {\tau _{ri}}]^{\text{T}}}$为模型不确定导致的摄动干扰；${\boldsymbol{R}}({\psi _i}) \in {{\bf{R}}^{3 \times 3}}$为坐标旋转矩阵；${y_i} = {[{y_{xi}},{y_{yi}},{y_{\psi i}}]^{\text{T}}}$为传感器测量输出；${{\boldsymbol{n}}_i} = {[{n_{xi}},{n_{yi}},{n_{\psi i}}]^{\text{T}}}$为传感器测量噪声。

1.4   协同路径跟踪误差模型

如图1所示，${\eta _{{\text{d}}i}}({\theta _i}) = ({x_{{\text{d}}i}}({\theta _i}),{y_{{\text{d}}i}}({\theta _i}))$为USVi的参数化期望路径，${\theta _i}$为路径参数。特殊地，${\eta _{{\text{d}}0}}({\theta _0}) = ({x_{{\text{d0}}}}({\theta _0}),{y_{{\text{d0}}}}({\theta _0}))$为虚拟领航艇的参数化路径，其路径参数满足$\dot{\theta}_0=v_{\mathrm{s}}$，$v_{\mathrm{s}}$为参考速度。基于USVi的位置$({x_i},{y_i})$与期望路径点$({x_{{\text{d}}i}}({\theta _i}),{y_{{\text{d}}i}}({\theta _i}))$，定义协同系统路径跟踪位置误差

式中：$x_{\mathrm{e}i}$为纵向位置误差；$y_{\mathrm{e}i}$为横向位置误差；${\psi _{{\text{d}}i}} = {\text{atan}}2\left( {{y'_{{\text{d}}i}},{x'_{{\text{d}}i}}} \right)$为路径切向角，$\text{atan}2(·)$为四象限反正切函数，${x'_{{\text{d}}i}} = {{\partial {x_{{\text{d}}i}}({\theta _i})}/{\partial {\theta _i}}}$与${y'_{{\text{d}}i}} = \partial {y_{{\text{d}}i}}({\theta _i})$$/\partial {\theta _i}$分别为路径点横纵坐标对路径参数的偏导数。

为保证多艘USV能够以预设队形进行协同路径跟踪任务，定义USVi的路径参数协同误差

式中，${l_{i0}}$为路径参数${\theta _i}$与${\theta _0}$之间的偏差量。

令${\boldsymbol{\theta }} = {[{\theta _1},{\theta _2}, \ldots ,{\theta _N}]^{\text{T}}}$，${\boldsymbol{L}} = {[{l_{10}},{l_{20}}, \ldots ,{l_{N{\text{0}}}}]^{\text{T}}}$，则式（4）可改写为

式中，$\mathcal{B}_i^{} \in {{\bf{R}}^{1 \times {N}}}$与${\mathcal{L}_i} \in {{\bf{R}}^{1 \times {N}}}$分别为邻接矩阵$\mathcal{B}$和拉普拉斯矩阵$\mathcal{L}$的第i行。

对式（3）与式（5）进行求导，并将式（2）代入得如下跟踪误差模型：

式中：${U'_{{\text{d}}i}} = \sqrt {x_{{\text{d}}i}^{\prime 2} + y_{{\text{d}}i}^{\prime 2}}$；${\psi _{\text{e}i}} = {\psi _i} - {\psi _{{\text{d}}i}}$；${\dot \theta _i} = {\hat v_{\text{s}i}} - {\varpi _i}$，$\hat{v}_{\mathrm{s}i}$为USVi的参考速度估计值，${\varpi _i}$为待设计的路径参数协同律。

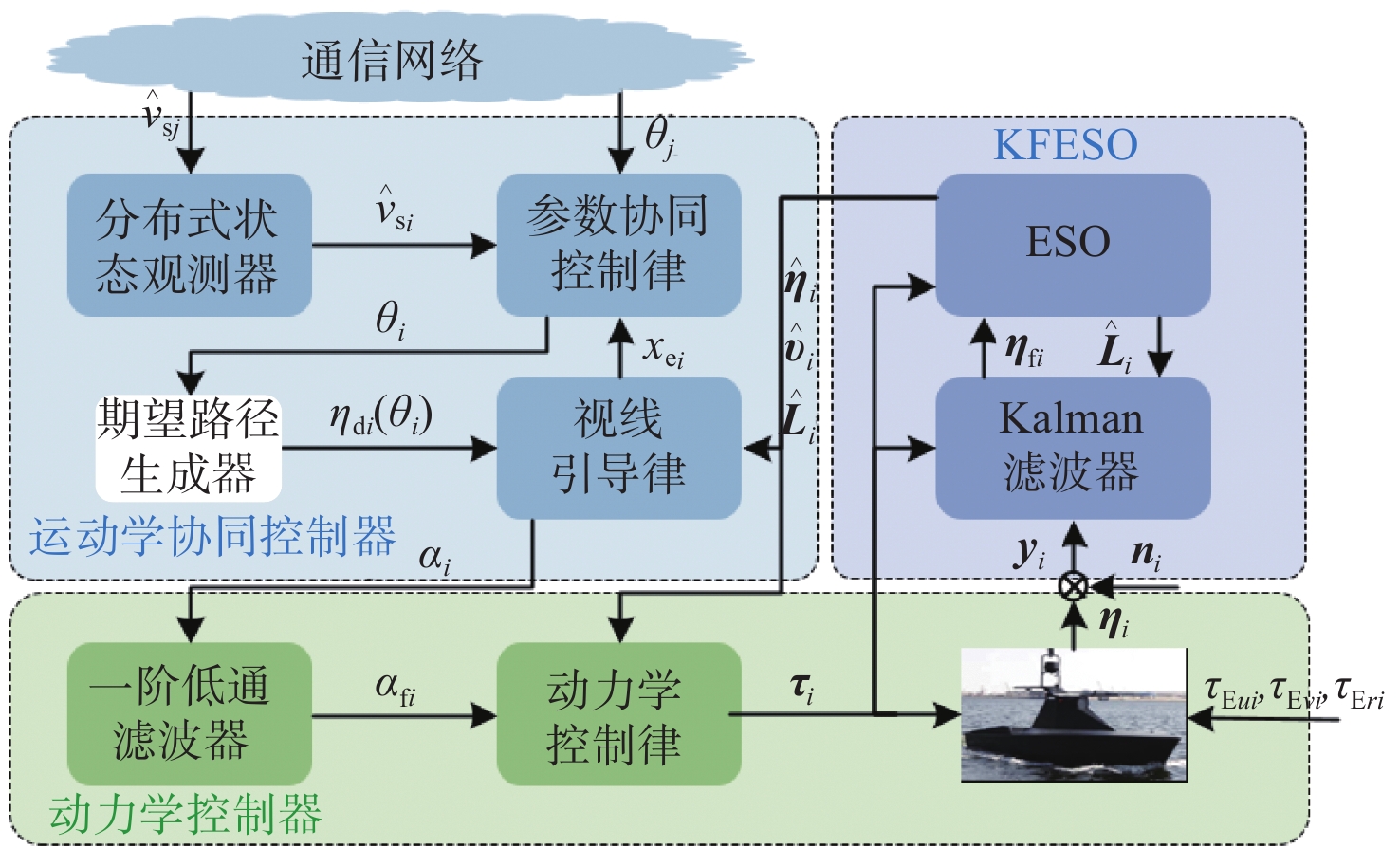
本文研究的协同路径跟踪控制目标为：在存在未知环境干扰、模型不确定动态以及传感器测量噪声等高低频混合多源干扰下，基于USV数学模型（2）以及协同路径跟踪误差模型（6），设计多艇分布式协同路径跟踪控制器，其控制结构如图2所示，使得多艇协同系统能够完成下述控制目标。

图  2  协同路径跟踪控制结构图

Figure  2.  Control structure diagram of coordinated path following

下载: 全尺寸图片 幻灯片

1） 几何目标

式中，$\varepsilon_{x\mathrm{e}i}$与$\varepsilon_{y\mathrm{e}i}$均为正常量。

2） 路径参数协同目标

式中，${\varepsilon _{e\theta i}}$为正常量。

2.   KFESO设计

为简化后续动力学控制器的设计过程，定义如下符号：

式中：${{\boldsymbol{B}}_{\tau i}} = {[{{\boldsymbol{B}}_{\tau ui}},{{\boldsymbol{B}}_{\tau vi}},{{\boldsymbol{B}}_{\tau ri}}]^{\text{T}}} \in {{\bf{R}}^{3 \times 3}}$为控制系数矩阵；${\hat \psi _i}$表示艏向角${\psi _i}$的估计值；${\boldsymbol{\varDelta }}{{\boldsymbol{F}}_i} = [\varDelta {F_{ui}},\varDelta {F_{vi}},$$\varDelta {F_{ri}}{]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$为由模型参数摄动导致的不确定动态；${\boldsymbol{F}} = {[{F_{ui}},{F_{vi}},{F_{ri}}]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$为系统非线性动态；${\boldsymbol{d}} =[{d_{ui}}, {d_{vi}},{d_{ri}}]^{\text{T}} \in {{\bf{R}}^{3 \times 1}}$为未知时变环境干扰；${{\boldsymbol{L}}_i} = [{L_{ui}},{L_{vi}}, {L_{ri}}]^{\text{T}} \in {{\bf{R}}^{3 \times 1}}$为集总扰动。

令${\mathcal{X}_{1i}} = {{\boldsymbol{\eta }}_i}$，${\mathcal{X}_{2i}} = {\dot {\boldsymbol{\eta}} _i}$，则基于式（2）与式（9），USVi的数学模型可简化为

令${{\boldsymbol{X}}_i} = {[\mathcal{X}_{1i}^{\text{T}},\mathcal{X}_{2i}^{\text{T}}]^{\text{T}}} \in {{\bf{R}}^{6 \times 1}}$，上式可进一步转化为如下紧凑格式：

式中：矩阵${{\boldsymbol{A}}_i} \in {{\bf{R}}^{6 \times 6}}$为状态转移矩阵；${{\boldsymbol{B}}_i} \in {{\bf{R}}^{6 \times 3}}$为控制系数矩阵；${{\boldsymbol{E}}_i} \in {{\bf{R}}^{6 \times 3}}$为扰动系数矩阵；$C_i\in\boldsymbol{\mathrm{\mathbf{R}}}^{3\times6}$为输出系数矩阵。各矩阵具体形式如下：

为保证后续控制器设计的合理性，现对多艇协同系统做出如下假设：

假设1：系统的集总扰动项${{\boldsymbol{L}}_i}$对其所有自变量都是连续可微的。${{\boldsymbol{L}}_i}$与其导数${\dot {\boldsymbol{L}}_i} = {{\boldsymbol{h}}_i}$有界，即满足${{\boldsymbol{L}}_i} \leqslant {\boldsymbol{L}}_i^*,{\boldsymbol{L}}_i^* = {[L_{ui}^*,L_{vi}^*,L_{ri}^*]^{\text{T}}}$，${{\boldsymbol{h}}_i} \leqslant {\boldsymbol{h}}_i^*,{\boldsymbol{h}}_i^* = {[h_{ui}^*,h_{vi}^*,h_{ri}^*]^{\text{T}}}$，$L_{ui}^*,L_{vi}^*,L_{ri}^*,h_{ui}^*,h_{vi}^*,h_{ri}^*$均为正常数。

假设2：传感器测量噪声${{\boldsymbol{n}}_i}$以及集总扰动估计误差${{\boldsymbol{\tilde L}}_i}$均为高斯白噪声，其均值为0，噪声协方差矩阵分别为${\Re _i} \in {{\bf{R}}^{3 \times 3}}$和${{\boldsymbol{\varTheta}} _i} \in {{\bf{R}}^{3 \times 3}}$；传感器测量噪声${{\boldsymbol{n}}_i}$有界，即满足${{\boldsymbol{n}}_i} \leqslant {\boldsymbol{n}}_i^*,{\boldsymbol{n}}_i^* = {[n_{xi}^*,n_{yi}^*,n_{\psi i}^*]^{\text{T}}}$，$n_{xi}^*,n_{yi}^*,n_{\psi i}^*$均为正常数。

假设3：多艇协同系统中的通信网络存在一棵以虚拟领航艇为根节点的生成树，即对任意USVi，均有一条有向路径使得信息可以从节点${n_0}$传输到节点${n_i}$。

基于假设1与假设2，式（11）可简化为如下扩张形式：

令${\bar {\boldsymbol{X}}_i} = {[{\boldsymbol{X}}_i^{\text{T}},{\boldsymbol{L}}_i^{\text{T}}]^{\text{T}}} \in {{\bf{R}}^{9 \times 1}}$，式（13）可进一步改写为

式中，矩阵${\bar {\boldsymbol{A}}_i} \in {{\bf{R}}^{9 \times 9}}$，${\bar {\boldsymbol{B}}_i} \in {{\bf{R}}^{9 \times 3}}$，${\bar {\boldsymbol{D}}_i} \in {{\bf{R}}^{9 \times 3}}$，${\bar {\boldsymbol{C}}_i} \in {{\bf{R}}^{3 \times 9}}$分别为式（11）中对应矩阵的扩张形式，各矩阵具体形式分别为：

基于扩张形式的系统模型（式（14）），设计如下KFESO：

式中，${{\boldsymbol{X}}_{\mathrm{f}i}} = {[\mathcal{X}_{\mathrm{f1}i}^{\text{T}},\mathcal{X}_{\mathrm{f2}i}^{\text{T}}]^{\text{T}}} \in {{\bf{R}}^{6 \times 1}}$为${{\boldsymbol{X}}_i}$的滤波值，$\mathcal{X}_{\mathrm{f}1i}^{} = {{\boldsymbol{\eta }}_{\mathrm{f}i}} = {[{x_{\mathrm{f}i}},{y_{\mathrm{f}i}},{\psi _{\mathrm{f}i}}]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$，$\mathcal{X}_{\mathrm{f}2i}^{ }=\boldsymbol{R}^{\text{T}}(\psi_{\mathrm{f}i})\boldsymbol{\upsilon}_{\mathrm{f}i}^{ }$，${\boldsymbol{\upsilon }}_{\mathrm{f}i}^{} = [{u_{\mathrm{f}i}}, {v_{\mathrm{f}i}},{r_{\mathrm{f}i}}]^{\text{T}} \in {{\bf{R}}^{3 \times 1}}$；${\hat {\bar {\boldsymbol{X}}}_i} = {[\hat {\mathcal{X}}_{1i}^{\text{T}},\hat {\mathcal{X}}_{2i}^{\text{T}},{\boldsymbol{\hat L}}_i^{\text{T}}]^{\text{T}}} \in {{\bf{R}}^{9 \times 1}}$为${\bar {\boldsymbol{X}}_i}$的估计值，$\hat {\mathcal{X}}_{1i}^{} = {{\boldsymbol{\hat \eta }}_i} = {[{\hat x_i},{\hat y_i},{\hat \psi _i}]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$，$\hat {\mathcal{X}}_{2i}^{} =$${{\boldsymbol{R}}^{\text{T}}}\left( {{{\hat \psi }_i}} \right){\hat {\boldsymbol{\upsilon }}_i}$，${\hat {\boldsymbol{\upsilon }}_i} = [{\hat u_i},{\hat v_i},{\hat r_i}{{\text{]}}^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$，${{\boldsymbol{\hat L}}_i} = {[{\hat L_{ui}},{\hat L_{vi}},{\hat L_{ri}}]^{\text{T}}}$$\in {{\bf{R}}^{3 \times 1}}$；$K_{\mathrm{K}i}\in\mathrm{\boldsymbol{\mathbf{R}}}^{6\times3}$为Kalman滤波器增益系数；${{\boldsymbol{K}}_{\mathrm{E}i}} \in {{\bf{R}}^{9 \times 3}}$为ESO增益系数，其具体形式为

式中：${{\boldsymbol{K}}_{\mathrm{E}1i}} = {\text{diag}} ( {k_{\mathrm{E}xi}},{k_{\mathrm{E}yi}},{k_{\mathrm{E}\psi i}} ) \in {{\bf{R}}^{3 \times 3}}$；${{\boldsymbol{K}}_{\mathrm{E}2i}} = {\text{diag}}\left( {{k_{\mathrm{E}ui}},} \right.$ $\left. {{k_{\mathrm{E}vi}},{k_{\mathrm{E}ri}}} \right) \in {{\bf{R}}^{3 \times 3}}$；${{\boldsymbol{K}}_{\mathrm{E}3i}} = {\text{diag}}\left( {{k_{\mathrm{E}Lui}},} \right.{k_{\mathrm{E}Lvi}},\left. {{k_{\mathrm{E}Lri}}} \right) \in {{\bf{R}}^{3 \times 3}}$。

定义滤波误差${{\boldsymbol{\tilde X}}_{\mathrm{f}i}} = {{\boldsymbol{X}}_i} - {{\boldsymbol{X}}_{\mathrm{f}i}} = {[\tilde {\mathcal{X}}_{\mathrm{f}1i}^{\text{T}},\tilde {\mathcal{X}}_{\mathrm{f}2i}^{\text{T}}]^{\text{T}}}$$\in {{\bf{R}}^{6 \times 1}}$，$\tilde {\mathcal{X}}_{\mathrm{f}1i}^{} = {\boldsymbol{\tilde \eta }}_{\mathrm{f}i}^{} = {[{\tilde x_{\mathrm{f}i}},{\tilde y_{\mathrm{f}i}},{\tilde \psi _{\mathrm{f}i}}]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$，$\tilde {\mathcal{X}}_{\mathrm{f}2i}^{} = {{\boldsymbol{R}}^{\text{T}}}\left( {{\psi _i}} \right)$${\boldsymbol{\tilde \upsilon }}_{\mathrm{f}i}^{} + ({{\boldsymbol{R}}^{\text{T}}}({\psi _i}) - {{\boldsymbol{R}}^{\text{T}}}({\psi _{\mathrm{f}i}})){\boldsymbol{\upsilon }}_{\mathrm{f}i}^{}$，${\boldsymbol{\tilde \upsilon }}_{\mathrm{f}i}^{} = \left[ {{{\tilde u}_{\mathrm{f}i}},{{\tilde v}_{\mathrm{f}i}},} \right.{\left. {{{\tilde r}_{\mathrm{f}i}}} \right]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$。将滤波误差${{\boldsymbol{\tilde X}}_{\mathrm{f}i}}$对时间t进行求导，并将式（14）与式（16）代入，得误差动态方程

定理1：在满足假设1与假设2的前提下，若Kalman增益$\boldsymbol{K}_{\mathrm{K}i}$满足如下条件：

则估计值${{\boldsymbol{X}}_{\mathrm{f}i}}$为最优估计值。${{\boldsymbol{P}}_{\mathrm{K}i}} \in {{\bf{R}}^{6 \times 6}}$为状态误差${{\boldsymbol{\tilde X}}_{\mathrm{f}i}}$的协方差矩阵，其具体形式为

式中，$E(·)$为均值函数。

证明：结合假设2，可得${\bar {\boldsymbol{n}}_i}$的协方差矩阵为

求解式（18），得

将式（22）代入式（20），可得

式（23）对时间t进行求导，得

定义代价函数$J = tr({{\boldsymbol{P}}_{\mathrm{K}i}}(t))$，并对增益系数${{\boldsymbol{K}}_{\mathrm{K}i}}$求偏导，得

由上式可知，当${{\boldsymbol{K}}_{\mathrm{K}i}} = {{\boldsymbol{P}}_{\mathrm{K}i}}{\boldsymbol{C}}_i^{\text{T}}\Re _i^{ - 1}$时，代价函数J处于最小值，${{\boldsymbol{X}}_{\mathrm{f}i}}$为最优估计值。

将式（25）代入式（24），得

综上，当增益系数${{\boldsymbol{K}}_{\mathrm{K}i}}$满足式（19）时，滤波误差${{\boldsymbol{\tilde X}}_{\mathrm{f}i}}$的协方差矩阵的迹最小，即${{\boldsymbol{X}}_{\mathrm{f}i}}$为最优估计值，定理1证毕。

定义估计误差${\tilde {\bar {\boldsymbol{X}}}_i} = {\bar {\boldsymbol{X}}_i} - {\hat {\bar {\boldsymbol{X}}}_i} = {[\tilde {\mathcal{X}}_{1i}^{\text{T}},\tilde {\mathcal{X}}_{2i}^{\text{T}},{\boldsymbol{\tilde L}}_i^{\text{T}}]^{\text{T}}}$$\in {{\bf{R}}^{9 \times 1}}$。其中，$\tilde {\mathcal{X}}_{1i}^{} = {\boldsymbol{\tilde \eta }}_i^{} = {[{\tilde x_i},{\tilde y_i},{\tilde \psi _i}]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$，$\tilde {\mathcal{X}}_{2i}^{} =$${{\boldsymbol{R}}^{\text{T}}}\left( {{\psi _i}} \right){\boldsymbol{\tilde \upsilon }}_i^{} + ({{\boldsymbol{R}}^{\text{T}}}({\psi _i}) - {{\boldsymbol{R}}^{\text{T}}}({\hat \psi _i}))\hat {\boldsymbol{\upsilon }}_i^{}$，${\boldsymbol{\tilde \upsilon }}_i^{} = {[{\tilde u_i},{\tilde v_i},{\tilde r_i}]^{\text{T}}} \in {{\bf{R}}^{3 \times 1}}$，${\boldsymbol{\tilde L}}_i^{} = [{\tilde L_{ui}}, {\tilde L_{vi}},{\tilde L_{ri}}]^{\text{T}} \in {{\bf{R}}^{3 \times 1}}$分别为${\bar {\boldsymbol{X}}_i}$，${\boldsymbol{\eta }}_i^{}$，${\boldsymbol{\upsilon }}_i^{}$，${\boldsymbol{L}}_i^{}$的估计误差。定义KFESO的估计误差为${{\boldsymbol{e}}_{{\text{KFESO}}i}} \in {{\bf{R}}^{15 \times 1}}$，其具体形式可表述为

式中，${{\boldsymbol{A}}_{{\text{KFESO}}i}}$，${{\boldsymbol{d}}_{{\text{KFESOi}}}} \in {{\bf{R}}^{15 \times 1}}$，其具体形式为：

定理2：在满足假设1与假设2的前提下，通过选择合适的参数使得${{\boldsymbol{A}}_{{\text{KFESO}}i}}$为Hurwitz矩阵，即存在正定矩阵${{\boldsymbol{P}}_{{\text{KFESO}}i}} \in {{\bf{R}}^{15 \times 15}}$，致使如下李雅普诺夫方程成立：

且正定矩阵${{\boldsymbol{P}}_{{\text{KFESO}}i}}$满足

则由式（27）组成的闭环系统中的所有误差信号一致最终有界。

证明：定义${V_{{\text{KFESO}}i}} = \frac{1}{2}{\boldsymbol{e}}_{{\text{KFESO}}i}^{\text{T}}{{\boldsymbol{P}}_{{\text{KFESO}}i}}{{\boldsymbol{e}}_{{\text{KFESO}}i}}$，并对时间t进行求导，得

由引理2，可知

式中，${\lambda }_{\mathrm{max}}(·)$为方阵的最大特征值。

令${\mu _{{\text{KFESO}}i}} = {1 / {{\lambda _{\max }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right)}} - 1$，${c_{{\text{KFESO}}i}} = {\left\| {{\boldsymbol{d}}_{{\text{KFESO}}i}^*} \right\|^2}$ ${{{\lambda _{\max }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right)} / 2}$。

求解式（32），可得

进一步得

由上式可知，${{\boldsymbol{e}}_{{\text{KFESO}}i}}$一致最终有界，其最终的界为$\sqrt {{{{c_{{\text{KFESO}}i}}} \mathord{\left/ {\vphantom {{{c_{{\text{KFESO}}i}}} {\left( {{\lambda _{\min }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right){\mu _{{\text{KFESO}}i}}} \right)}}} \right. } {\left( {{\lambda _{\min }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right){\mu _{{\text{KFESO}}i}}} \right)}}}$，定理2证毕。

3.   运动学协同控制器设计

不同于集中式控制结构，在多艇分布式协同系统中，USV仅可与邻居USV进行通信，即并非所有USV均可获取虚拟领航艇的参考速度。为估计虚拟领航艇速度信息，基于一致性理论设计如下分布式状态观测器：

令$\tilde{v}_{\mathrm{s}i}^{ }=v\mathrm{_s}-\hat{v}_{\mathrm{s}i}^{ }$，${{\boldsymbol{\tilde v}}_\mathrm{s}} = {\left[ {\tilde v_{\mathrm{s}1}^{},\tilde v_{\mathrm{s}2}^{}, \ldots ,\tilde v_{\mathrm{s}{N}}^{}} \right]^{\text{T}}} \in {{\bf{R}}^{{N} \times 1}}$，则分布式状态观测器的估计误差动态方程为

基于KFESO的状态估计值，式（6）可改写为

式中，${{\boldsymbol{\hat v}}_\mathrm{s}} = {[{\hat v_{\mathrm{s}1}},{\hat v_{\mathrm{s}2}}, \ldots ,{\hat v_{\mathrm{s}N}}]^{\text{T}}}$；$\varpi {\text{ = [}}{\varpi _1},{\varpi _2}, \ldots ,{\varpi _N}{{\text{]}}^{\text{T}}}$。

令${\alpha _{ui}}$，${\alpha _{\psi i}}$，${\alpha _{ri}}$分别为纵向速度、艏向角、转艏角速度虚拟控制量；${\psi _{\mathrm{e}i}} = {\hat \psi _i} - {\alpha _{\psi i}}$，${\tilde \alpha _{ui}} = {\hat u_i} - {\alpha _{ui}}$，${\tilde \alpha _{ri}} = {\hat r_i} - {\alpha _{ri}}$；${\rho _i} = \sin ({\psi _{{\text{d}}i}} - {\alpha _{\psi i}} - {\text{atan}}2({\hat v_i},{\hat u_i})) - \sin$$( {\psi _{{\text{d}}i}} - {\psi _i} - {\text{atan}}2\left( {{{\hat v}_i},{{\hat u}_i}} \right))$。设计如下运动学协同控制律：

式中：${\varDelta _i}$为前向距离；${k_{ui}}$，${k_{ri}}$，${k_{\theta x}}$，${k_{\theta e}}$均为待设计的正常数。

将式（16）与式（38）代入式（37），得位置协同误差方程：

式中：${{\boldsymbol{x}}_\mathrm{e}} = {\left[ {{x_{\mathrm{e}1}},{x_{\mathrm{e}2}}, \ldots ,{x_{\mathrm{e}N}}} \right]^{\text{T}}} \in {{\bf{R}}^{N \times 1}}$；${{\boldsymbol{e}}_\theta } = [{e_{\theta {\text{1}}}},{e_{\theta {\text{2}}}}, \ldots ,$${e_{\theta N}}{]^{\text{T}}} \in {{\bf{R}}^{N \times 1}}$。

4.   动力学控制器设计

令速度虚拟控制量${{\boldsymbol{\alpha }}_i} = {[{\alpha _{ui}},{\alpha _{ri}}]^{\text{T}}}$。为避免求取虚拟控制量导数复杂的解析解，引入动态面技术，将虚拟控制量输入至一阶低通滤波器中，有

式中：${{\boldsymbol{\alpha }}_{\mathrm{f}i}} = {\left[ {{\alpha _{\mathrm{f}ui}},{\alpha _{\mathrm{f}ri}}} \right]^{\text{T}}}$为虚拟控制量${{\boldsymbol{\alpha }}_i}$滤波后的值；${\rho _{\mathrm{f}i}} = {\text{diag}}\left( {{\rho _{\mathrm{f}ui}},{\rho _{\mathrm{f}ri}}} \right)$为一阶低通滤波器的时间常数，${\rho _{\mathrm{f}ui}}$与${\rho _{\mathrm{f}ri}}$均为正常数。

定义滤波误差${{\boldsymbol{\tilde \alpha }}_{\mathrm{f}i}} = {{\boldsymbol{\alpha }}_i} - {{\boldsymbol{\alpha }}_{\mathrm{f}i}}{\text{ = [}}{\tilde \alpha _{\mathrm{f}ui}},{\tilde \alpha _{\mathrm{f}ri}}{{\text{]}}^{\text{T}}}$，对时间t进行求导并将式（40）代入，得

定义速度误差${{\boldsymbol{q}}_i} = {[{q_{ui}},{q_{ri}}]^{\text{T}}}$，其具体形式为

式中，${\boldsymbol{H}} = \left[ {\begin{array}{*{20}{l}} 1&0&0 \\ 0&0&1 \end{array}} \right]$为投影矩阵。

式（42）对时间t进行求导，并将式（14）与式（40）代入，得

基于式（43）设计如下动力学控制律：

式中，${{\boldsymbol{K}}_{\text{c}i}} \in {{\bf{R}}^{2 \times 2}}$为待设计的正定对角矩阵。

将式（44）代入式（43），得速度误差动态方程

5.   稳定性分析

在由N艘USV构成的协同路径跟踪控制系统中，构造李雅普诺夫预选函数V，其具体形式为

令${V_1} = \dfrac{1}{2}[\sum\nolimits_{i = 1}^N {\left( {x_{\mathrm{e}i}^2 + y_{\mathrm{e}i}^2 + \psi _{\mathrm{e}i}^2} \right)} + {\boldsymbol{e}}_\theta ^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{e}}_\theta } + {\boldsymbol{\tilde v}}_\mathrm{s}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{\tilde v}}_\mathrm{s}}]$，将其对时间t进行求导并代入式（39），得

由假设3、引理1与引理2进一步得

式中：${\boldsymbol{G}} = {k_{\theta x}}{\boldsymbol{P}}\left( {\mathcal{L} + \mathcal{B}} \right) + {{\boldsymbol{U}}'_{\text{d}}}$，${{\boldsymbol{U}}'_{\text{d}}} = {\text{diag}}\left( {{U'_{\text{d}1}}, \ldots ,{U'_{\text{d}N}}} \right)$；${\boldsymbol{M}} = {\boldsymbol{P}}\left( {\mathcal{L} + \mathcal{B}} \right)$；${\Vert ·\Vert }_{\text{F}}$为Frobenius范数。

令${{\boldsymbol{y}}_\text{e}} = {\left[ {{y_{\text{e}1}},{y_{\text{e}2}} \ldots ,{y_{\text{e}N}}} \right]^{\text{T}}}$；${{\boldsymbol{\psi }}_\text{e}} = {\left[ {{\psi _{\text{e}1}},{\psi _{\text{e}2}} \ldots ,{\psi _{\text{e}N}}} \right]^{\text{T}}}$；${\varsigma _{x\text{e}i}} = {k_{ui}} + {k_{\theta i}}{U'_{\text{d}i}} - 1 - {k_{\text{E}xi}} - {k_{\text{E}yi}}$，${\varsigma _{y\text{e}i}} = {{{{\hat U}_i}}/ {\sqrt {y_{\text{e}i}^2 + \varDelta _i^2} }} - {k_{\text{E}xi}}$$- {k_{\text{E}yi}}$，${\varsigma _{\psi \text{e}i}} = {k_{ri}} - 1 - {k_{\text{E}\psi i}}$；${K_{x\text{e}}} = {\lambda _{\min }}({\text{diag(}}{\varsigma _{x\text{e}1}}, \ldots ,{\varsigma _{x\text{e}N}}{\text{)}}) -$${\left\| {\boldsymbol{G}} \right\|_{\text{F}}}$，${K_{y\text{e}}} = {\lambda _{\min }}({\text{diag}}({\varsigma _{y\text{e}1}}, \ldots ,{\varsigma _{y\text{e}N}}))$，${K_{\psi \text{e}}} = {\lambda _{\min }}($${\text{diag}}({\varsigma _{\psi \text{e}1}}, \ldots ,{\varsigma _{\psi \text{e}N}}))$，则式（48）可简化为

令${V_2} = \dfrac{1}{2}\sum\nolimits_{i = 1}^N {{\boldsymbol{q}}_i^{\text{T}}{{\boldsymbol{q}}_i}} + \dfrac{1}{2}\sum\nolimits_{i = 1}^N {{\boldsymbol{\tilde \alpha }}_{\mathrm{f}i}^{\text{T}}{{{\boldsymbol{\tilde \alpha }}}_{\mathrm{f}i}}}$，将其对时间t进行求导并将式（45）代入，得

${\dot {\boldsymbol{\alpha }}_i}$为连续向量函数，满足${\dot {\boldsymbol{\alpha }}_i} \leqslant {\boldsymbol{\alpha }}_i^*$，${\boldsymbol{\alpha }}_i^* = {[\alpha _{ui}^*,\alpha _{ri}^*]^{\text{T}}}$，$\alpha _{ui}^*$与$\alpha _{ri}^*$均为正常数。

令${k_{v1}} = \min \left\{ {2{K_{x\text{e}}},2{K_{y\text{e}}},2{K_{\psi \text{e}}},\dfrac{{{k_{\theta \text{e}}}{\lambda _{\min }}\left( {\boldsymbol{Q}} \right) - {{\left\| {\boldsymbol{G}} \right\|}_{\text{F}}} - {{\left\| {\boldsymbol{M}} \right\|}_{\text{F}}}}}{{{\lambda _{\max }}\left( {\boldsymbol{P}} \right)}}}, \right.$ $\left. {\dfrac{{{k_{v\text{s}}}{\lambda _{\min }}\left( {\boldsymbol{Q}} \right) - {{\left\| {\boldsymbol{M}} \right\|}_{\text{F}}}}}{{{\lambda _{\max }}\left( {\boldsymbol{P}} \right)}}} \right\}$,${k_{v2}} = \min \{ - 2{\lambda _{\max }}\left( {{{\boldsymbol{K}}_{\text{E}2i}}} \right){\left\| {\boldsymbol{H}} \right\|_{\text{F}}} + 2{\lambda _{\min }}$ $\left( {{{\boldsymbol{K}}_{\text{c}i}}} \right),1 - 2{\lambda _{\min }}\left( {{\boldsymbol{\rho }}_{\mathrm{f}i}^{ - 1}} \right)\}$，结合式（33）、式（49）与式（51），V对时间t的导数为

令${k_{v1}} = \min \Bigg\{ {{\mu _{{\text{KFESO}}i}} - \dfrac{{{\text{2}}{\lambda _{\max }}\left( {{{\boldsymbol{K}}_{E1i}}} \right)}}{{{\lambda _{\max }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right)}} - \dfrac{{{\lambda _{\max }}\left( {{{\boldsymbol{K}}_{E2i}}} \right){{\left\| {\boldsymbol{H}} \right\|}_{\text{F}}}}}{{{\lambda _{\max }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right)}},}$${{k_{v1}},{k_{v2}} - 1} \Bigg\}$，${c_{v1}} = \dfrac{1}{2}\sum\nolimits_{i = 1}^N {{{\left( {\alpha _i^*} \right)}^2}} + \sum\nolimits_{i = 1}^N {{c_{{\text{KFESO}}i}}}$，则对式（52）进一步化简得

定理3：考虑由N艘USV构成的协同路径跟踪控制系统，在满足假设1至假设3、定理1、定理2的前提下，采用KFESO（式（16）），运动学协同控制器（式（38）），动力学控制器（式（44）），使得相应参数满足

则闭环系统中的所有误差信号一致最终有界。

证明：由式（53）与式（54），可得

令${{\boldsymbol{e}}_v} \in {{\bf{R}}^{{\text{24}}N \times 1}}$表示USV协同路径跟踪复合抗扰控制系统中的所有误差信号，其满足

式中，${\text{min}}\left\{ {{\lambda _{\min }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right),{\lambda _{\min }}\left( {\boldsymbol{P}} \right),\dfrac{1}{2}} \right\}{\left\| {{{\boldsymbol{e}}_{v1}}} \right\|^2}$与${\text{max}}\Bigg\{ {\lambda _{\max }} \left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right),{\lambda _{\max }}\left( {\boldsymbol{P}} \right),\dfrac{1}{2} \Bigg\}{\left\| {{{\boldsymbol{e}}_v}} \right\|^2}$均为${\mathcal{K}}$类函数。

由式（55）与式（56），进一步得

由式（56）与式（57）可知，${{\boldsymbol{e}}_v}$一致最终有界，其最终的界为$\sqrt {{{{c_v}} / {\left( {{k_v}{\text{min}}\left\{ {{\lambda _{\min }}\left( {{{\boldsymbol{P}}_{{\text{KFESO}}i}}} \right),{\lambda _{\min }}\left( {\boldsymbol{P}} \right),0.5} \right\}} \right)}}}$，定理3证毕。

6.   仿真结果与分析

6.1   仿真条件

为验证所提方法的有效性，针对由3艘欠驱动USV组成的协同系统进行仿真试验，其通信拓扑结构如图3所示。其中，虚拟领航艇编号为USV0，跟随艇编号分别为USV1，USV2，USV3。

图  3  通信拓扑网络

Figure  3.  Communication topology networks

下载: 全尺寸图片 幻灯片

仿真中采用的USV模型为Cybership Ⅱ模型，该模型为单体船型，其推进系统由2个主推进器与2个尾舵组成，具体水动力参数见文献[25]。各USV的初始位置分别为${\eta _1}(0)$=[3.5 m, 3.5 m, −30°]^T，${\eta _2}(0)$=[−33.9 m, −38.9 m, −30°]^T,${\eta _3}(0)$=[−41 m, 46 m, −30°]^T。初始速度均为${{\boldsymbol{\upsilon }}_i}\left( 0 \right)$=[0 m/s, 0 m/s, 0 （°）/s]^T。路径参数的参考速度为$v_{\mathrm{s}}=0.5$。参数偏差为${\boldsymbol{L}} = {[0, -6, -6]^{\text{T}}}$。不确定动态为$\varDelta {{\boldsymbol{M}}_i} = 0.2{{\boldsymbol{M}}_i}$, $\varDelta {{\boldsymbol{C}}_i}({{\boldsymbol{\upsilon}} _i}) = 0.2{{\boldsymbol{C}}_i}({{\boldsymbol{\upsilon}} _i})$, $\varDelta {{\boldsymbol{D}}_i}({{\boldsymbol{\upsilon}} _i}) = 0.2{{\boldsymbol{D}}_i}({{\boldsymbol{\upsilon}} _i})$。风、浪、流等海洋环境引起的外界环境干扰分别设置为$\tau_{\text{E}ui}=\left(0.1\sin\left(0.005\mathrm{{\text{π}}}t-\mathrm{{\text{π}}}/5\right)-0.1u^2vr\right)$ N, ${\tau _{{\text{E}}vi}} = (0.1$ $\sin \left( {0.005{\text{π}} t + {{\text{π}} / 6}} \right) - 0.1u{v^2}r)$ N, ${\tau _{{\text{E}}ri}} = (0.01\sin ({{\text{π}} /3}+$ $0.005{\text{π}} t) - 0.01uv{r^2})$ N·m。传感器测量噪声协方差设置为${\Re _i} = {\text{diag}}[{(0.1{\text{ m}})^2},{(0.1{\text{ m}})^2},{({2.9^{\text{o}}})^2}]$。

针对本章所设计的USV协同路径跟踪复合抗扰控制方法，选取KFESO参数分别为$\boldsymbol{K}_{\mathrm{E}1i}= \text{diag}\left(2.0,2.0,3.0\right)$，$\boldsymbol{K}_{\mathrm{E}2i}=\text{diag}\left(0.5,0.5,1.8\right)$，$\boldsymbol{K}_{\mathrm{E}3i}= \text{diag} \left(0.1,0.1,0.4\right)$，${{\boldsymbol{\varTheta}} _i} = {\text{diag}}[{({10^{ - 4}}{{\text{ m}} / {{{\text{s}}^2}}})^2},{({10^{ - 4}}{{\text{ m}} /{{{\text{s}}^2}}})^2},$ $({10^{ - 4}} {{{\text{ rad}}} /{{{\text{s}}^2}}})^2]$。选取运动学协同控制器参数分别为${k_{v\text{s}}} = 0.5$，${\varDelta _i} = 5$，${k_{ui}} = 0.1$，${k_{ri}} = 0.5$，${k_{\theta xi}} = 0.1$，${k_{\theta \text{e}i}} = 0.9$。选取动力学控制器参数分别为${{\boldsymbol{K}}_{\text{c}i}} = {\text{diag}}\left( {0.1,2.5} \right)$，${\rho _{\mathrm{f}i}} = {\text{diag}}(1.0,1.0)$。

为便于后续阐述，将本文所设计方法命名为方法1。与此同时，为验证所设计方法的优越性，设计基于标准ESO的抗扰控制方法，并将其作为对比方法，命名为方法2。其中，标准ESO为

为保证对比分析的公平性，标准ESO参数的设置与KFESO相同，且运动学协同控制器和动力学控制器同方法一。

6.2   结果与分析

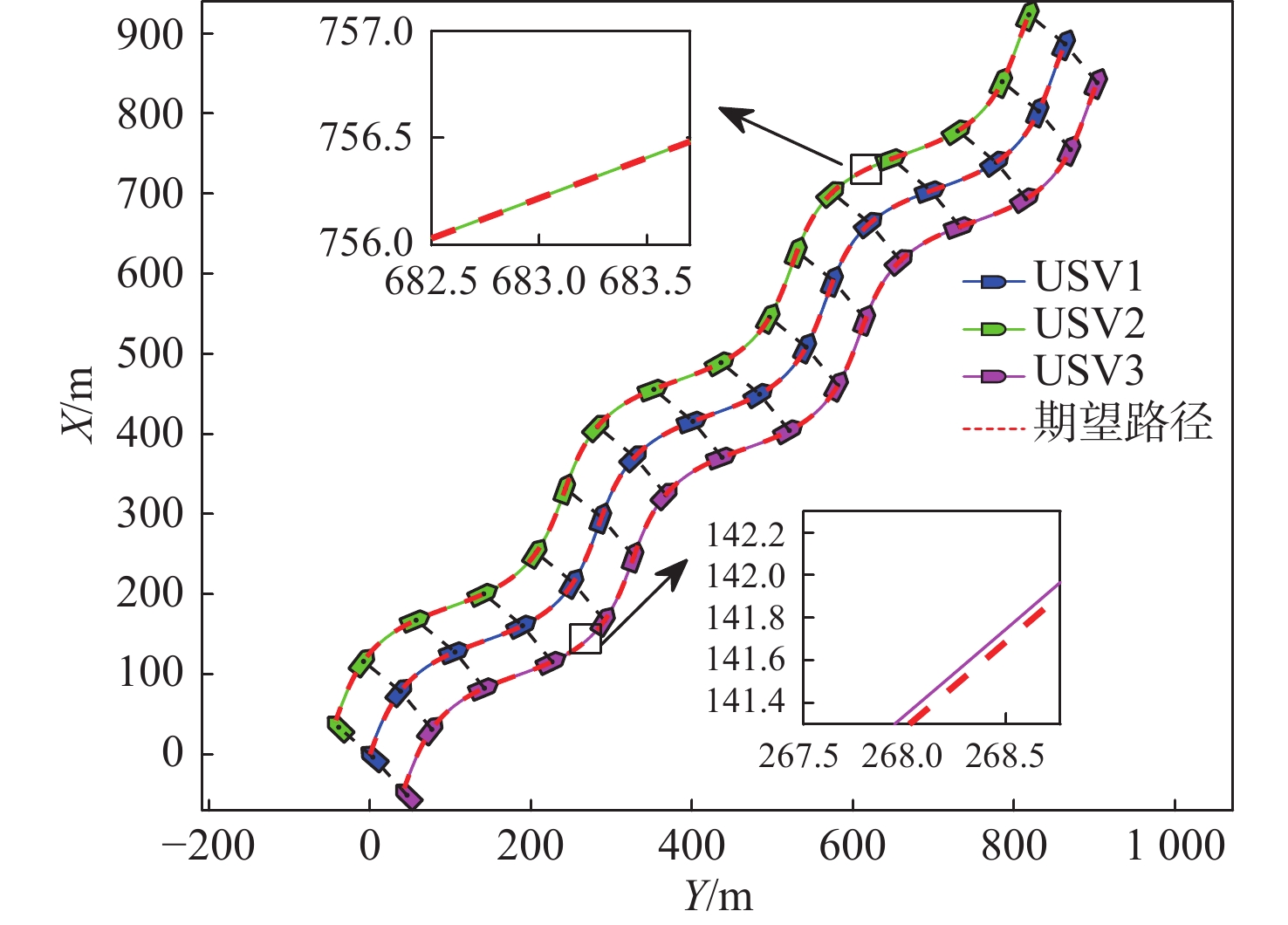
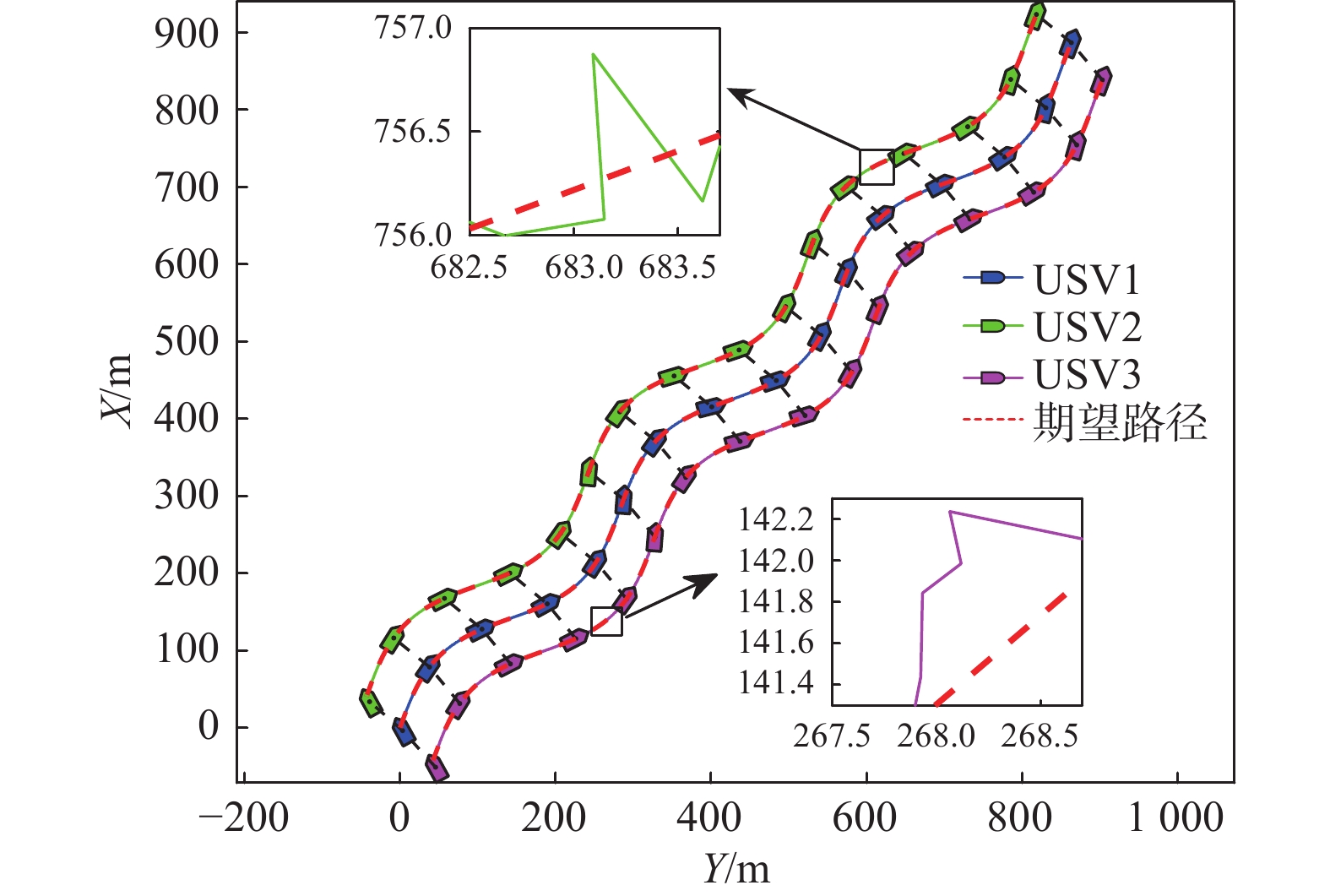
图4与图5为2种方法下的实际路径跟踪轨迹图。从图中可以看出，2种方法均能使3艘USV沿着相应参考路径航行，并在航行过程中逐渐形成预设编队队形。与此同时，各图中的放大子图可以看出方法1的横向偏差最小，方法2则存在较大幅度抖动。

图  4  协同路径跟踪轨迹（方法1）

Figure  4.  Coordinated path following trajectory (method 1)

下载: 全尺寸图片 幻灯片

图  5  协同路径跟踪轨迹（方法2）

Figure  5.  Coordinated path following trajectory (method 2)

下载: 全尺寸图片 幻灯片

图6为位置误差对比图。从图中可以看出，2种方法下纵向、横向与艏向误差的收敛时间相近。但方法2在整个控制周期内存在频率较高的抖动，且各自由度误差的抖动幅值分别达0.2 m，0.2 m与0.5 rad。相比之下，方法1的误差曲线较为平滑，且不存在抖动现象。这是由于在方法2中，输入进运动学协同控制器中的USV位置与姿态信号仍然存在较大噪声，导致其在控制过程中响应噪声信号，致使位置/艏向误差存在较高频率的抖动。上述结果初步体现了方法1在存在噪声、时变环境干扰与模型不确定下的USV编队路径跟踪场景中具有更优的表现。

图  6  位置误差对比（左：方法2，右：方法1）

Figure  6.  Comparison of position errors under different methods (method 2 is on the left, and method 1 is on the right )

下载: 全尺寸图片 幻灯片

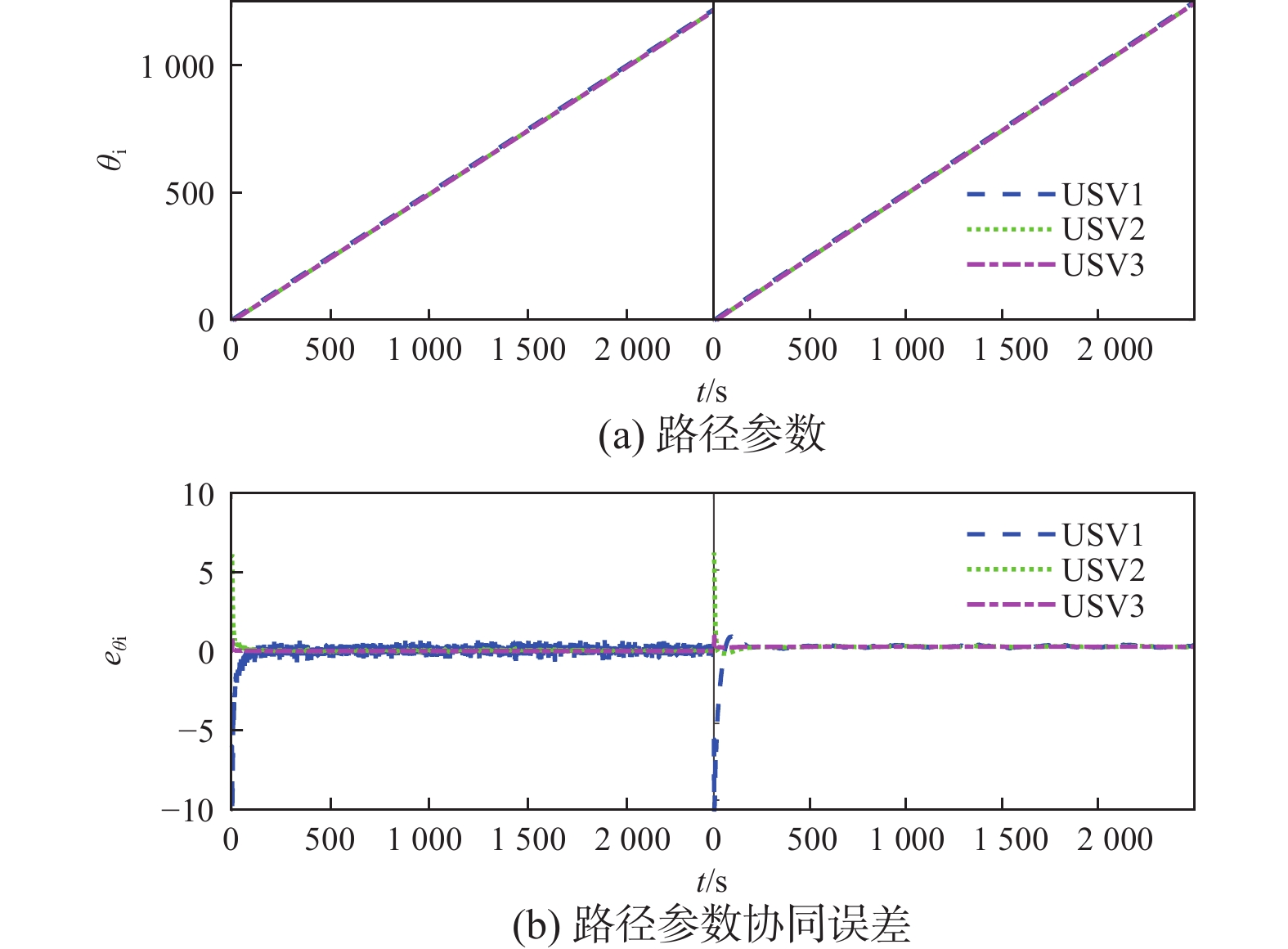
图7所示为2种方法下的路径参数与参数协同误差。从图中可以看出2种方法均能够使多艇协同系统逐步达到预设队形，进一步验证了图4与图5的结果。然而，方法2下的参数协同误差存在幅值为0.3的高频抖动，队形无法稳定，这是由于方法2中的纵向误差受到噪声影响，以致包含纵向误差的路径参数协同控制律存在高频抖动，进而无法使参数协同误差收敛至0。

图  7  路径参数与参数协同误差对比

Figure  7.  Comparison of path parameters and coordinated errors

下载: 全尺寸图片 幻灯片

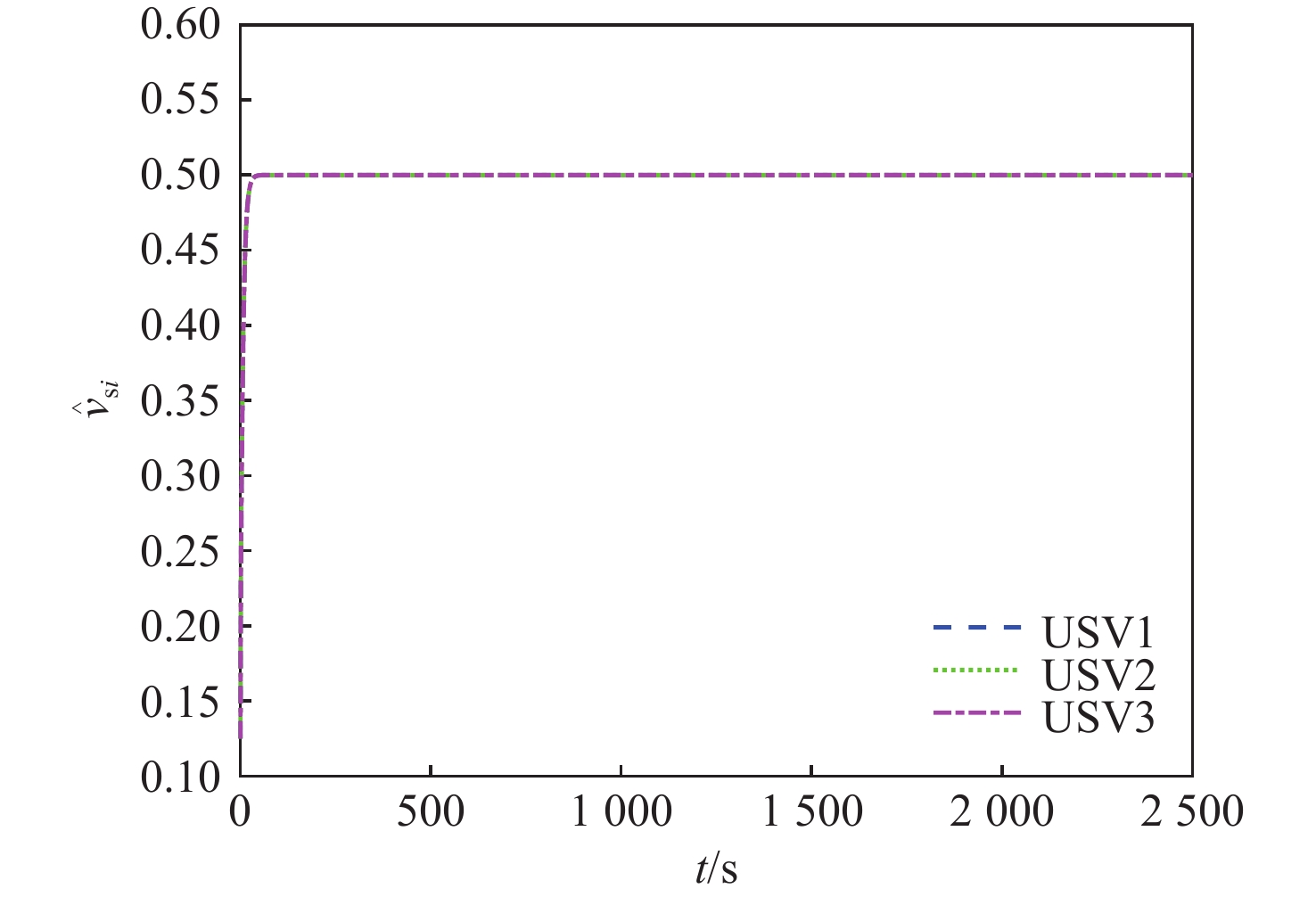
图8为分布式状态观测器估计结果图。由图可知，各USV参考速度估计值均能够在100 s内逐渐收敛至实际值0.5，且在整个过程中未出现超调现象，实现了USV在仅通过与邻居USV进行信息交互的条件下，估计出虚拟领航艇速度信息，验证了所设计分布式状态观测器的有效性。

图  8  分布式状态观测器估计结果

Figure  8.  Estimated value of distributed state observer

下载: 全尺寸图片 幻灯片

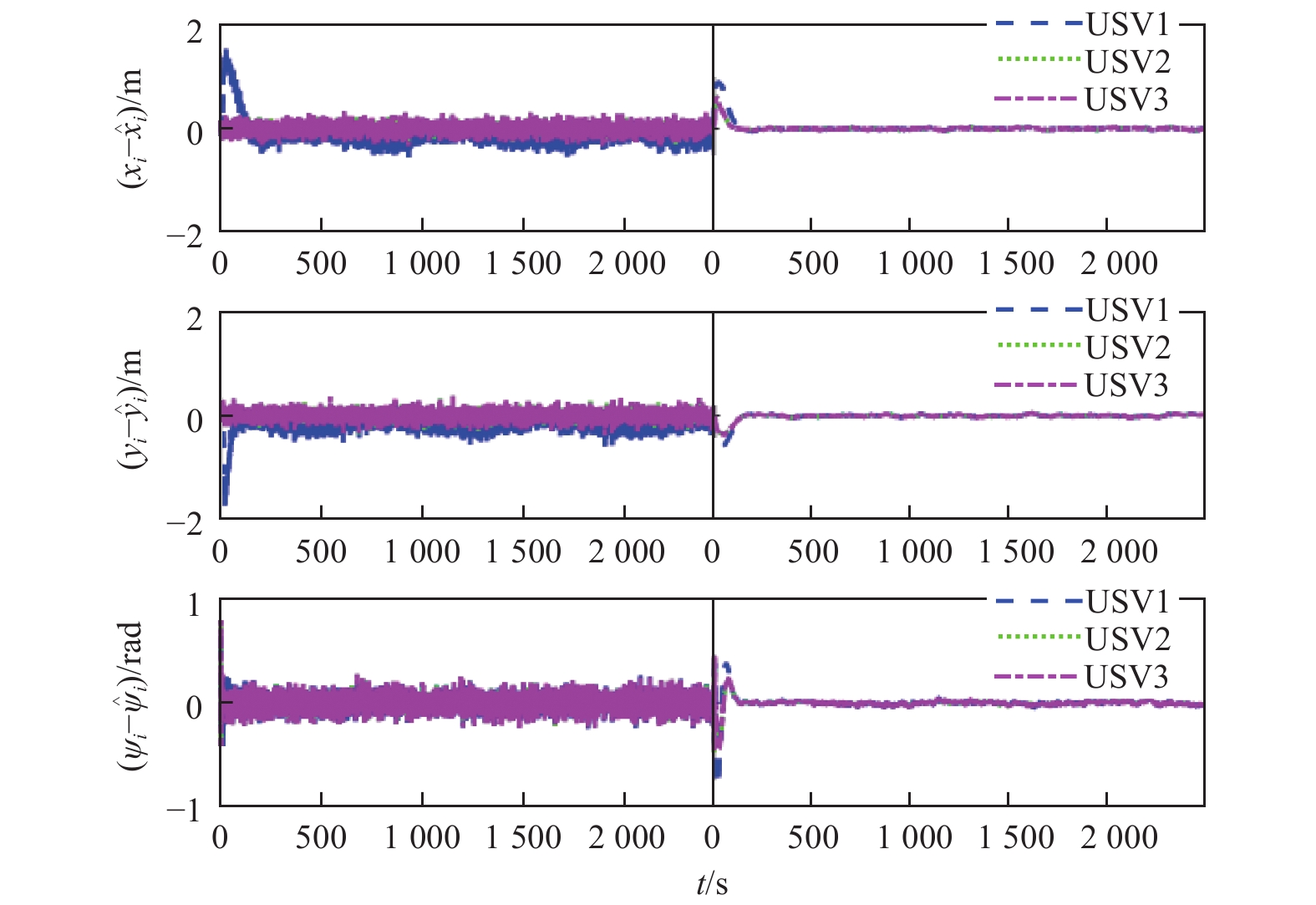
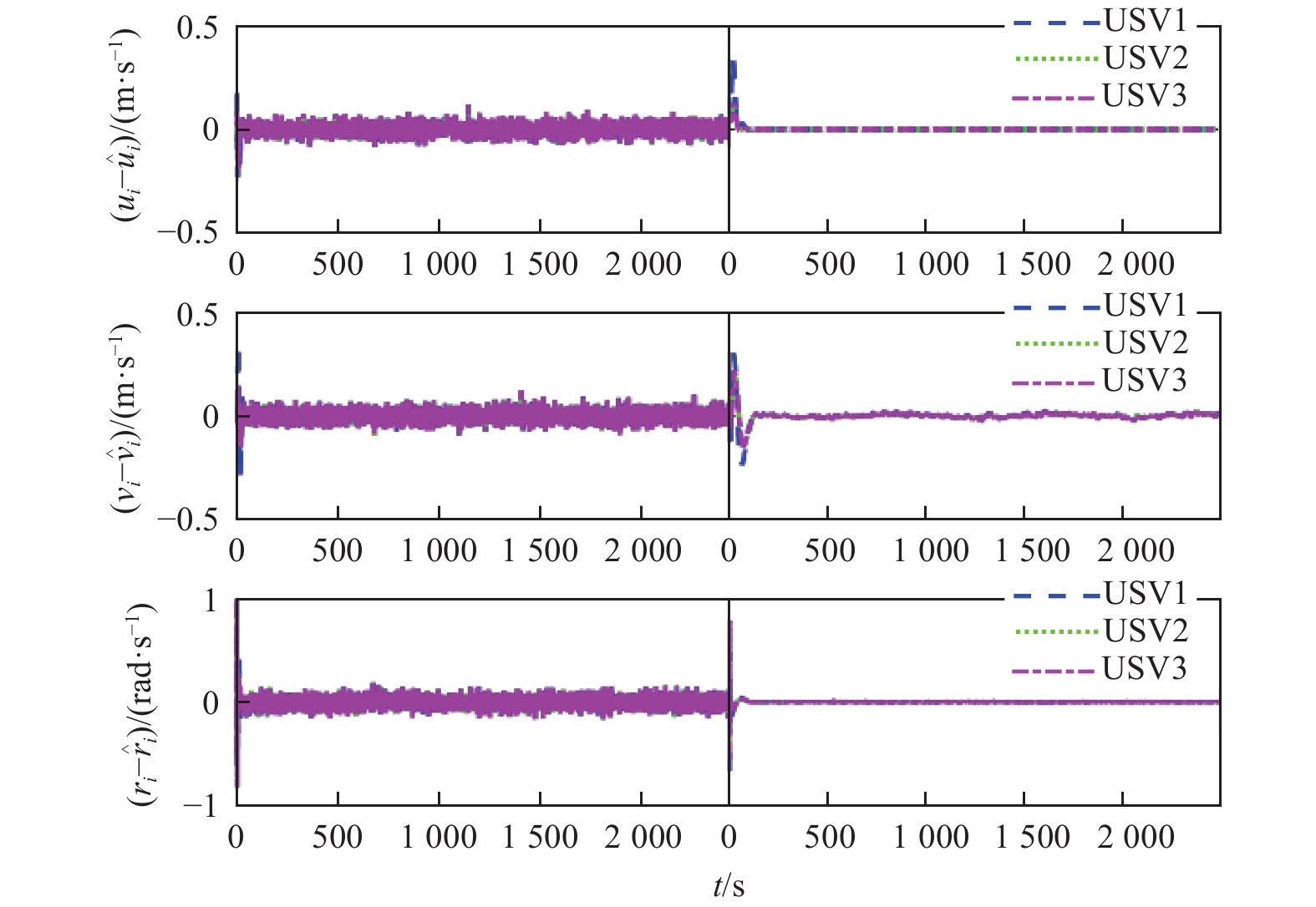
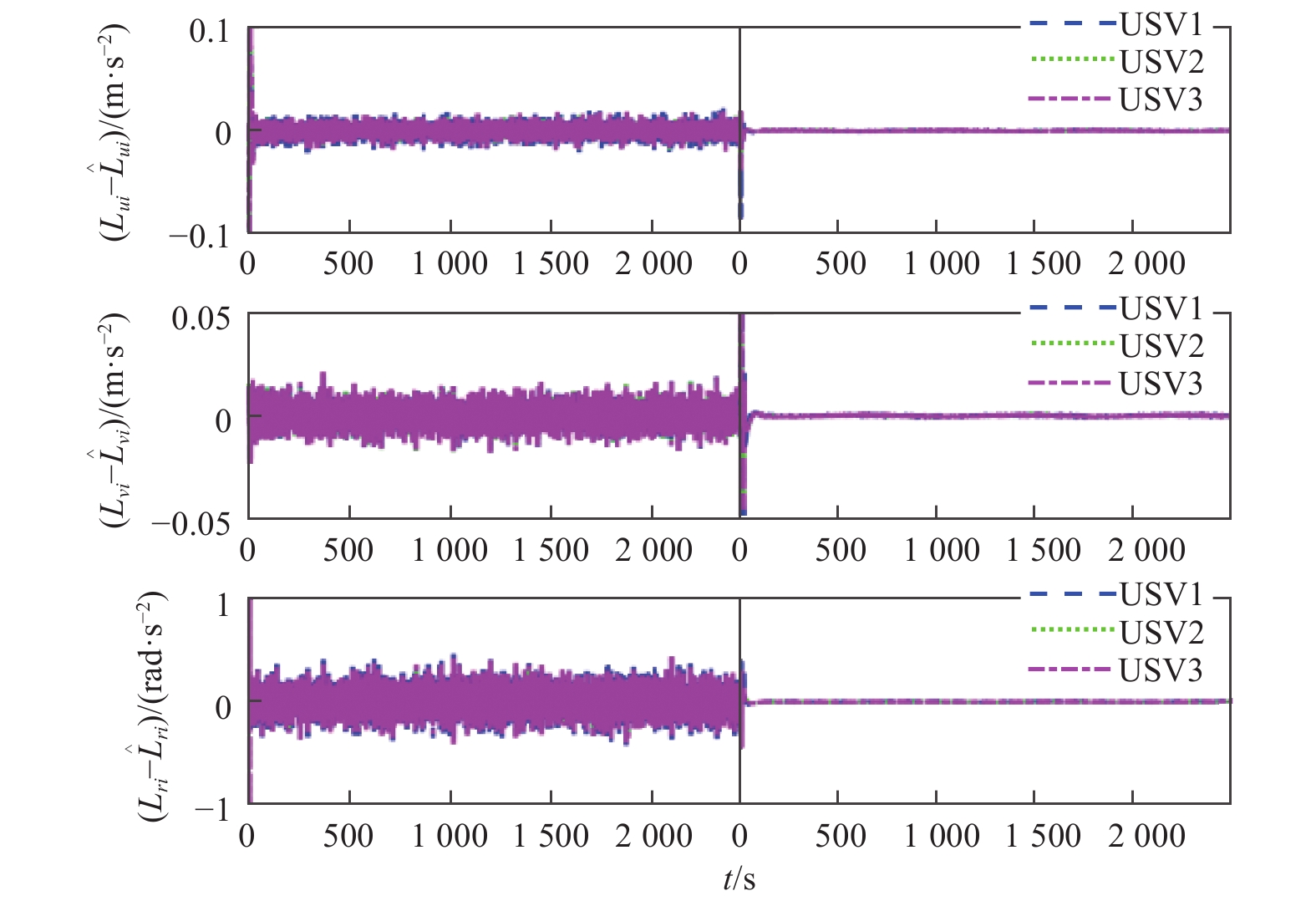
从图9～图11中可以看出方法2对USV各阶量的估计值中均存在频率较高的抖动，严重影响其估计精度。这是由于标准ESO存在估计速度与精度之间的矛盾，增益系数较高会使得其对应幅频特性在中频段斜率较小，有助于改善其动态性能，但却增大了ESO的带宽，使得对应的幅频特性在高频段较大，致使其滤波性能变差。此外，为定量分析2种方法下ESO对各阶量的估计精度且不失一般性，给出如表1～表3所示的USV1各阶量的估计误差均方值。从表中可以看出，方法1能够显著提高各阶量的估计精度。这是由于方法1在Kalman滤波器的作用下，能够对含有噪声的测量数据进行最优滤波，使得测量数据在输入进ESO前就已削弱高频噪声的影响。

表  2  USV1速度估计误差均方值

Table  2.  MSE of velocity estimation errors for USV1

方法	纵向速度 估计误差/(m·s−1)	横向速度 估计误差/(m·s−1)	转艏角速度 估计误差/(rad·s−1)
1	0.004 9	0.008 4	0.003 8
2	0.028 2	0.032 2	0.058 2

下载: 导出CSV 

| 显示表格

图  9  位置估计误差对比

Figure  9.  Comparison of position estimation errors

下载: 全尺寸图片 幻灯片

图  10  速度估计误差对比

Figure  10.  Comparison of velocity estimation errors

下载: 全尺寸图片 幻灯片

图  11  扰动估计误差对比

Figure  11.  Comparison of disturbance estimation errors

下载: 全尺寸图片 幻灯片

表  1  USV1位置估计误差均方值

Table  1.  MSE of position estimation errors for USV1

方法	北向位置 估计误差/m	东向位置 估计误差/m	艏向位置 估计误差/rad
1	0.018 5	0.023 5	0.016 7
2	0.273 0	0.244 6	0.081 3

下载: 导出CSV 

| 显示表格

表  3  USV1扰动估计误差均方值

Table  3.  MSE of disturbance estimation errors for USV1

方法	纵向扰动 估计误差/(m2·s−1)	横向扰动 估计误差/(m2·s−1)	艏向扰动 估计误差/(rad2·s−1)
1	0.004 9	0.008 4	0.003 8
2	0.028 2	0.032 2	0.058 2

下载: 导出CSV 

| 显示表格

图12为2种方法下的速度误差对比图。从图中可以看出，在相应动力学控制律的作用下，2种方法均可以在100 s内收敛。然而，方法2下的速度误差存在较高频率的抖动。图13为2种方法下的控制力（矩）对比图。从图中可以看出，方法2的纵向和转艏控制律分别存在幅值为1.5与2.5的高频振荡。这是由于标准ESO未能有效削弱测量噪声的影响，导致动力学控制器频繁响应包含噪声的速度估计信号，而方法1由于消除了测量噪声的影响，使得执行器能够平滑变换执行指令，进而能够有效防止其对噪声信号的响应，降低其磨损。

图  12  速度误差对比

Figure  12.  Comparison of velocity errors

下载: 全尺寸图片 幻灯片

图  13  控制力（矩）对比

Figure  13.  Comparison of control force (moment)

下载: 全尺寸图片 幻灯片

7.   结　语

本文针对高低频混合多源干扰导致的USV无法准确获取状态信息且路径跟踪精度低的问题，提出了一种基于KFESO的多艇分布式协同路径跟踪复合抗扰控制方法。并利用3艘USV进行仿真对比试验，验证了该控制方法的有效性。结果表明，在存在高低频混合多源干扰影响下，所提方法能够缓解标准ESO在估计速度与精度之间的矛盾，既能够有效去除高频测量噪声，又可以保证其快速获取USV各阶状态量。相较于基于标准ESO的协同路径跟踪控制方法，其能够避免后端执行器对噪声的频繁响应，且路径跟踪精度更高，抗扰性能更强。

本文虽然能够有效降低高频测量噪声的影响，但滤波器的参数设置需预先获取噪声的协方差，未来可通过应用自适应理论实现对噪声协方差的估计，进一步优化该控制方法。