Influence of Suboff stern structure on the wake field quality at propeller disk with fixed stern upwind area
-
摘要:目的
探究水下航行体桨盘面伴流场均匀性随尾翼位置和尾部去流角的变化规律，揭示航行体尾部结构对伴流场的影响机理。
方法采用计算流体力学（CFD）方法对水下航行体进行数值模拟分析，并对伴流场不均匀度指标进行高斯过程建模分析，探究设计范围内结构−流场的形性协同响应，分析Suboff尾部结构对伴流场不均匀度的敏感性，探寻伴流均匀的Suboff尾部结构。
结果结果显示，在固定尾翼迎流面积保证航行体操作性能和航行效率的情况下，尾翼位置和尾部去流角会对桨盘面不均匀度产生较大影响；当去流角θ = 10°时，尾翼后移会使桨盘面伴流目标函数（WOF）值从0.124 5降至0.091 4；当去流角θ = 20°时，尾翼后移会使桨盘面WOF值从0.104 9先升至0.114 5随后降至0.106 8；当尾翼轴向位置为3.810 0 m时，去流角增大会使桨盘面WOF值从0.124 5降至0.104 9；当尾翼轴向位置h = 4.114 8 m时，去流角的增大会加剧桨盘面的不均匀性，WOF值从0.091 4升至0.106 8；利用高斯过程建模分析和敏感性分析，改善Suboff的尾部结构能有效降低桨盘面伴流场的不均匀度。
结论研究表明，对于尾翼迎流面积不变的Suboff模型，大的尾翼轴向位置与小的尾部去流角配置可显著提升桨盘面伴流场的均匀性，能为水下航行体尾部结构设计提供指导依据。
Abstract:ObjectivesThis paper investigates the variation in the uniformity of the wake field on the propeller disk of an underwater vehicle according to the tail fin axial position and angle of run of the stern, and reveals the influence mechanism of the stern structure on the wake field.
MethodsNumerical simulation analysis of the underwater vehicle is carried out using the computational fluid dynamics (CFD) method, and Gaussian process modeling analysis is performed for the wake field inhomogeneity index to explore the response relationship between structure-field performance within the design range, analyze the sensitivity of the stern structure to wake field inhomogeneity, and search for a Suboff stern structure with excellent wake field homogeneity.
ResultsAs the results show, with a fixed tail fin axial upwind area to ensure the operation performance and sailing efficiency of the underwater vehicle, the tail fin axial position and angle of run of the stern have a large impact on the propeller disk inhomogeneity; when the angle of run of the stern is θ=10∘, the backward movement of the tail fin axial reduces the propeller disk inhomogeneity, and the wake objective function (WOF) decreases from 0.124 5 to 0.091 4; when the angle of run of the stern is θ=20∘, the backward movement of the tail fin axial causes the inhomogeneity of the propeller disk to first increase and then decrease, and the WOF increases from 0.1049 to 0.1145, then decreases to 0.1068; when the tail fin axial position is h=3.810 0 m, the increase of the angle of run of the stern makes the propeller disk inhomogeneity decrease, and the WOF decreases from 0.124 5 to 0.104 9; and when the tail fin axial position is h=4.114 8 m, the increase of the angle of run of the stern makes the propeller disk inhomogeneity increase, and the WOF increases from 0.091 4 to 0.106 8. This shows that the adjustment of the Suboff stern structure using Gaussian process modeling analysis can effectively reduce the inhomogeneity of the wake field on the propeller disk.
ConclusionsFor a Suboff model with a fixed stern upwind area, a configuration with a large tail fin axial position and small angle of run of the stern can significantly enhance the propeller disk wake field uniformity. The findings of this study can provide useful references for the design of the stern structures of underwater vehicles.
-
0. 引 言
水下航行体作为重要的海洋装备，被广泛应用于国民经济和军事领域。航行体尾部不均匀伴流与推进器相互作用导致的振动噪声对航行体水动力和噪声特性具有重要影响[1]。航行体型线变化、表面曲率不连续，以及航行体表面存在的围壳、尾翼等附体结构会使来流在航行体周围形成流动分离现象，从而诱发复杂涡系。涡团的形成和发展使得推进器在不均匀来流中工作，进而影响水下航行体的振动和噪声性能。因此，水下航行体周围流体的流动机理和航行体的结构特征对伴流场空间分布均匀性的影响受到国内外学者的广泛关注[2-3]。
早期，Huang等[4-6]通过试验研究，获取了Suboff标模的阻力、压力、桨盘面速度分布以及湍流强度、湍流剪切力等大量数据，为后续学者开展数值模拟研究提供了标模验证。随着计算流体力学（CFD）方法的快速发展，大量学者结合试验和数值计算开展了水下航行体伴流场的分布特征与调控策略研究。从水下航行体伴流场主动控制的角度，需考虑破碎主流涡团，改善桨盘面伴流场周向分布的不均匀性，探究围壳根部射流以及尾翼前部不同孔型射流对主附体结合处马蹄涡的破碎作用[7-8]；探讨在马蹄涡路径上增设消涡整流片等措施，以降低主流涡团的强度[9-10]。从水下航行体几何结构调控的角度，除了要探究艇体半径、艇首、艇尾等主体尺寸长度和形状对航行体尾部流场的影响[11-12]，由于水下航行体的附体结构显著影响桨盘面处伴流场，进而影响推进装置的激振力特性，研究者还应考虑降低附体结构对流场的扰动，从而减弱扰流涡团强度，提升航行体尾部伴流场的均匀性[13]。围壳和尾翼作为水下航行体主要的附体结构，附体形状、位置、尺寸、与主体的连接方式成为学者们重点关注的对象。其中，调整围壳形状仅对其后方流场有一定的影响，对桨盘面处流场的影响较小[14-15]。调整尾翼形状则对桨盘面处轴向速度的不均匀度影响较大[16]。改变附体位置，如围壳后移、尾翼等高度后移会减少尾流恢复和马蹄涡耗散的距离，使得桨盘面速度的不均匀度增大[17]。尾翼变高度后移时，对流场的扰动降低，湍流强度减小[18]。此外，尾翼周向分布位置也会对伴流场产生影响，相比十字型尾翼，X型尾翼能降低伴流场速度分布的标准差和极差，可改变航行体的水动力特性[14,19]。而调整附体尺寸，减小尾翼迎流面积，则可降低马蹄涡强度，提升速度的均匀性[20]。在主附体交接处添加填角，能够有效抑制该位置诱发的马蹄涡强度，提升尾流质量[21-22]。
特别地，水下航行体尾翼作为桨盘面速度场不均匀的主要诱因，前人的研究表明，尾翼位置、尺寸和迎流面积是相互耦合的影响因素。姜宜辰等[17]研究了尾翼轴向位置对伴流场的影响，结果显示当固定尾翼高度轴向平移时，其尺寸和面积会发生明显变化。而尾翼迎流面积是航行体稳定性、操纵性和阻力的重要影响因素[23]。Beigi等[18]在进行尾翼轴向位置的影响研究时，考虑了变动尾翼的高度，但未考虑固定尾翼的迎流面积。
综上，前人在研究航行体附体位置变化时，附体尺寸和迎流面积是协同变化的，并未剥离单一变量。此外，由附体引起的马蹄涡团是沿航行体尾部渐缩结构向下游输运耗散，从而造成了桨盘面速度场的不均匀分布。然而，关于航行体尾部去流角的研究相对匮乏，其对涡团输运的影响机理不明确。
为此，本文将以Suboff 模型为研究对象，在固定尾翼迎流面积的条件下，探究不同尾翼轴向位置和去流角对桨盘面不均匀度的影响，然后进一步基于参数化Suboff模型，利用高斯过程代理模型探究水下航行体尾部结构与伴流场性能指标之间的映射关系，为水下航行体尾部结构设计提供理论基础。
1. 数值模型
1.1 几何模型和计算域
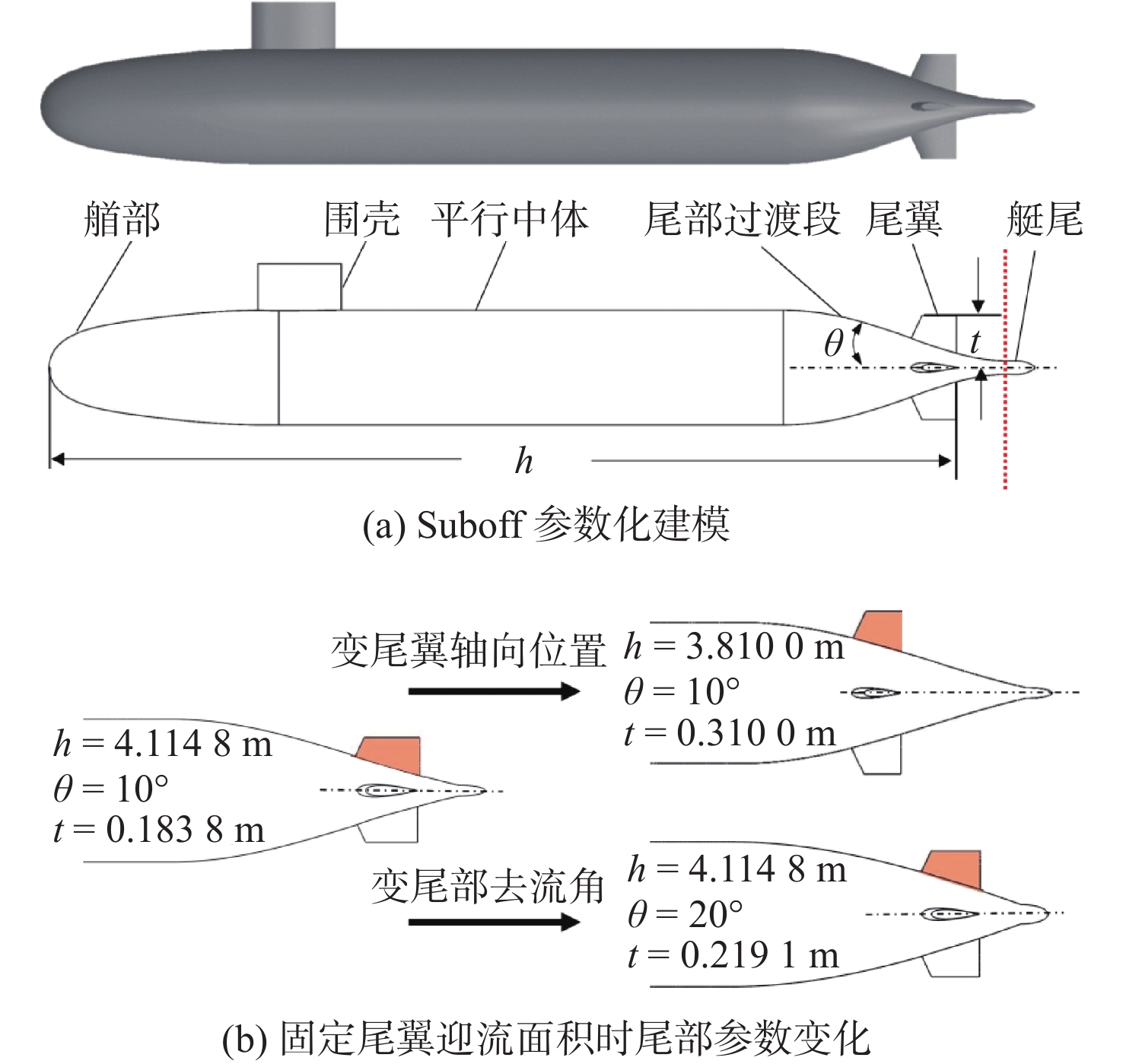
本文采用Suboff艇体作为标准模型，探究航行体尾部几何结构对桨盘面伴流场分布均匀性的影响。首先，对Suboff几何模型进行参数化建模，如图1（a）所示。
![]()
图 1 Suboff参数化建模及固定尾翼迎流面积时尾部参数变化示意图Figure 1. Suboff parametric modeling and the variation in tail parameters when the tail fin upwind area is fixed全艇的参数方程主要由艏部曲线、平行中体曲线、艇尾曲线、尾部过渡段曲线、指挥台围壳曲线和尾翼曲线构成。图1中：红色虚线表示桨盘面所在位置，距艏部顶端4.26 m；h为尾翼末端与艏部的轴向距离；θ为艇尾去流角；t为尾翼高度。
定义艇长为L，艇体直径为d，则尾部过渡段轮廓曲线的表达式为
r(z)=12d−(3d2c2−tanθc)(z−a−b)2+(dc3−tanθc2)(z−a−b)3 (1) 式中：z为轴向位置；r(z)为z位置处的尾部过渡段回转半径；参数a，b，c分别为艏部长度、平行中体长度和艉部过渡段长度。
不同尾翼高度水平截面轮廓曲线的表达式如下：
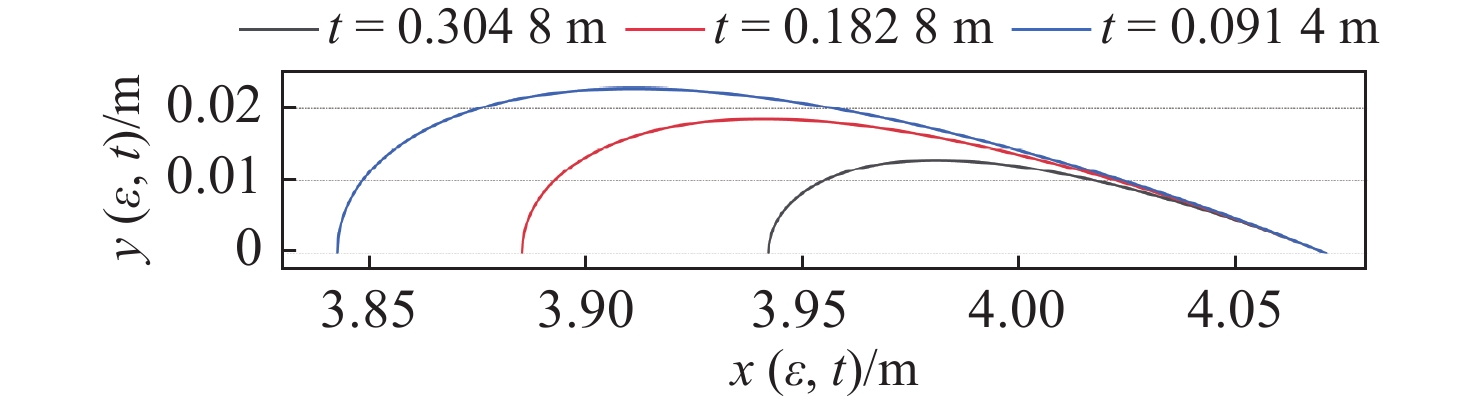
x(ε,t)=(−0.1421t+0.2708)(ε−1)+h (2) y(ε,t)=(−0.1421t+0.2708)×(0.2969ε0.5−0.1260ε−0.3516ε2+0.2852ε3−0.1045ε4) (3) 式中，0⩽。
图2所示为固定尾翼的尾缘点，尾翼高度 t 分别为0.304 8，0.182 8和0.091 4 m时的尾翼水平截面轮廓曲线。
尾翼的迎流面积S可积分为
{S = 2\int \limits_{r\left( {\textit{z}} \right)}^t \int \limits_0^1 \sqrt {{{\left( {{\text{d}}x\left( {\varepsilon ,t} \right)} \right)}^2} + {{\left( {{\text{d}}y\left( {\varepsilon ,t} \right)} \right)}^2}} {\text{d}}\varepsilon {\text{d}}t} (4) 本文选择Suboff模型尾部去流角 \theta 及尾翼末端与艏部的轴向距离h作为研究参数，固定尾翼在航行体轴心平面的基准叶型不变，通过调整尾翼高度t，保证尾翼迎流面积恒定为S = 0.040 412 m2，如图1（b）所示。
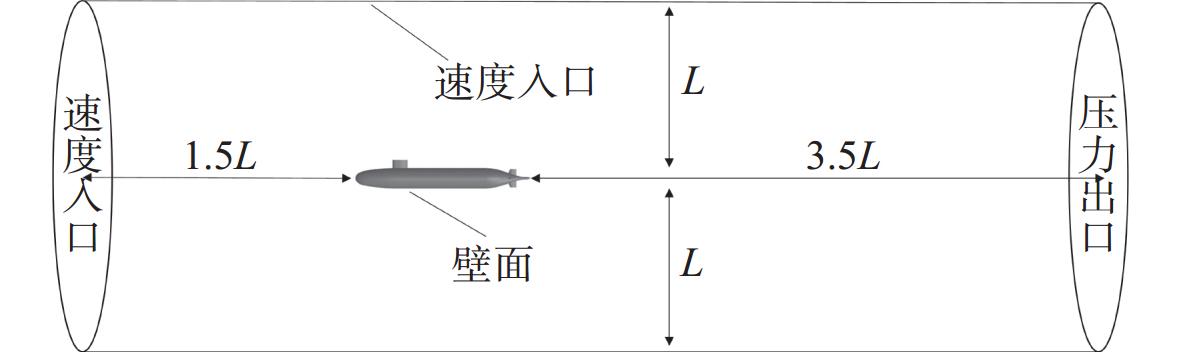
本文采用圆柱型计算域，采用速度入口和压力出口边界条件，艇体外表面设置为壁面，满足无滑移条件。计算域尺寸及边界条件设置如图3所示。
![]()
图 3 Suboff模型计算域及边界条件Figure 3. The computational domain and boundary conditions of Suboff model1.2 控制方程和湍流模型
全附体潜艇的尾部流场特征和水动力特征主要受艇后黏性尾流和漩涡等因素的影响。本文关注速度分布和水动力性能等宏观量，通过商用软件FLUENT，采用 RANS（Reynolds average Navier-Stokes）方法进行仿真求解。湍流模型采用剪切应力传输SST k-\omega 模型，控制方程离散采用二阶迎风格式，压力速度耦合迭代采用 SIMPLEC 算法。
1.3 网格划分与数值验证
通过FLUENT Meshing八叉树法生成非结构化计算网格，为准确捕捉近壁面区域和艇尾区域的流动特性，将计算域分为如图4所示的内、外3个区域进行逐级加密。为了探究网格密度对模拟精度的影响，采用4组不同密度的网格，计算入口速度为3.051 m/s时Suboff模型的阻力，并与实验值进行对比，结果如表1所示。以艇长为特征长度，可得来流雷诺数Re = 1.2×107。依照ITTC不确定度分析规程[24]，对计算网格的不确定度进行分析，得到网格收敛率RG = 0.485，说明网格单调收敛；网格不确定性UG = 1.988，数值较小，表明数值模拟的不确定度处于合理范围。当网格数量为2×107时，由数值仿真计算得到的阻力与实验结果间的相对误差约为1%。基于Suboff艇体计算域的对称性，取一半模型进行仿真计算。最后，考虑计算精度，采用的网格数约为107，外流域至艇体表面的网格尺寸分3层逐级加密，限制各级网格最大尺寸分别为0.005，0.02和0.06 m，如图4所示。
![]()
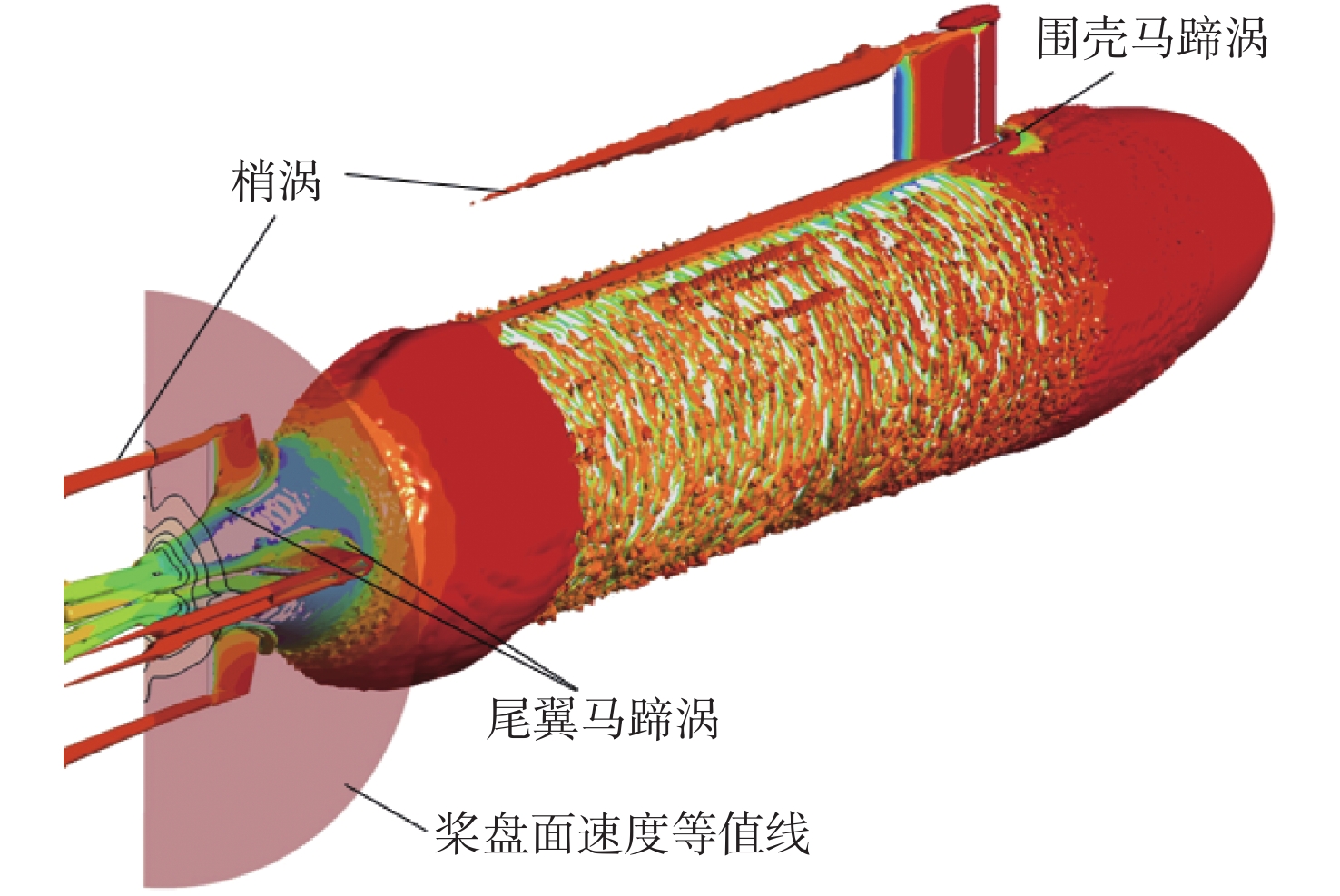
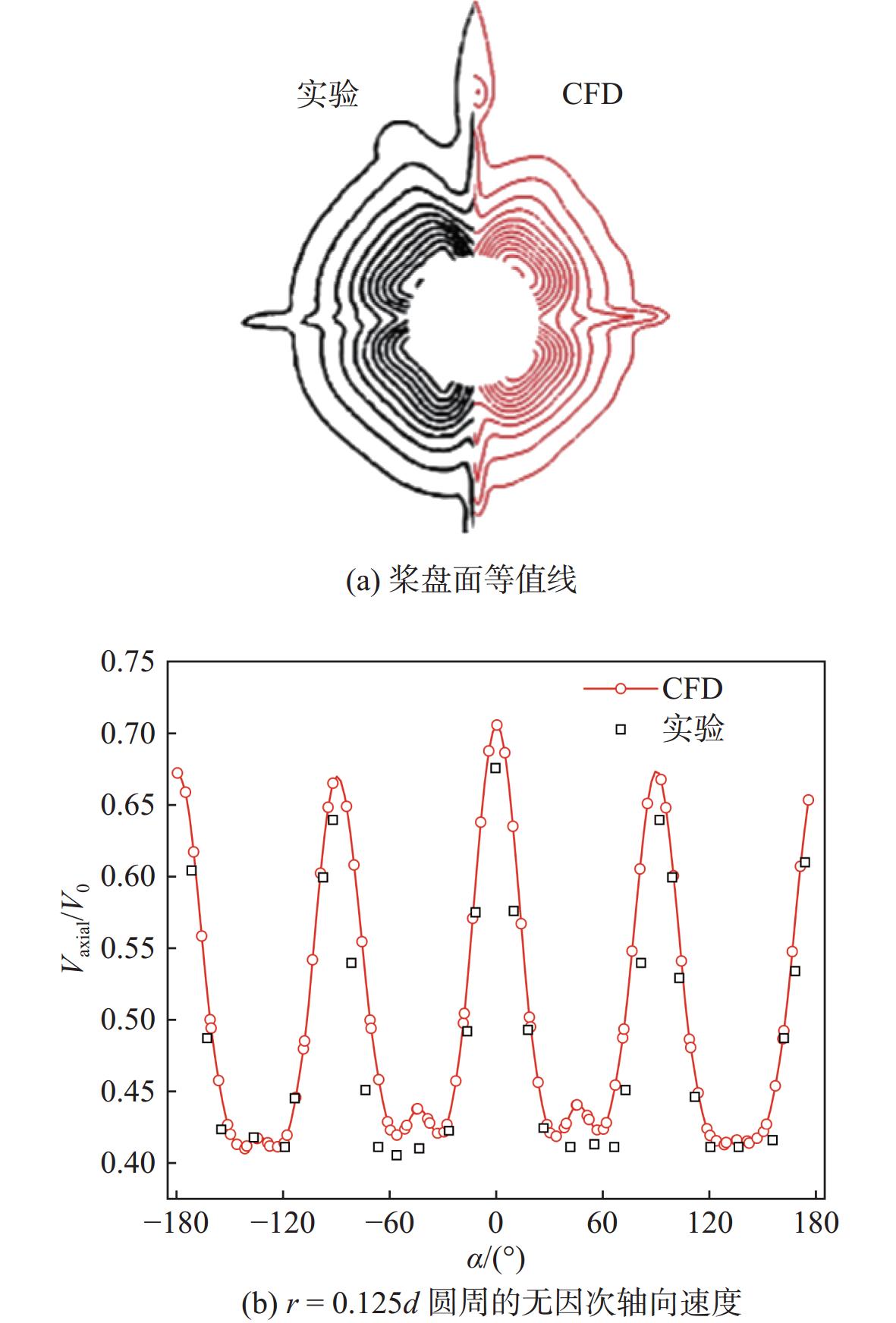
图 4 Suboff模型计算域非结构网格Figure 4. Unstructured grids for the computational domains of Suboff model表 1 Suboff模型阻力及误差Table 1. The resistance values and errors for the Suboff model网格数量 阻力/N 相对误差/% 实验 仿真 5.279×106 102.3 95.475 6.672 10.861×106 102.3 99.351 2.882 20.122×106 102.3 101.233 1.043 由于围壳、尾翼等附体结构对流场的扰动会引起涡系发展，使得桨盘面伴流场沿径向呈现不均匀性。如图5所示，附体梢涡和马蹄涡的存在分别促使了较大半径处和较小半径处速度场的减缓与增大，对应的等值线在较大半径处外凸，在较小半径处内凹。将数值模拟得到的桨盘面轴向速度与实验结果进行对比，最外层归一化速度为0.9，相邻两条等值线之间相差0.05。由图6（a）可以看到，两者桨盘面轴向速度的分布趋势相近，说明数值模拟结果能够表征Suboff模型桨盘面处的速度分布特征。
![]()
图 6 桨盘面无因次轴向速度对比Figure 6. Comparison of the normalized axial velocity on the propeller disk surface进一步地，提取桨盘面半径为0.125d圆周的无因次轴向速度，并与实验数据[4]进行对比，如图6（b）所示。结果显示，仿真数据与实验数据整体吻合较好，满足实际工程精度需求。图6（b）中：Vaxial为桨盘面轴向水流速度；V0为航速；\alpha 为周向角（逆时针为正）；围壳和上尾翼对应0°位置。
2. 尾部参数对桨盘面伴流品质的影响
2.1 伴流品质评价指标
为了量化比较水下航行体的伴流场质量，使用伴流目标函数（wake object function，WOF）[25]描述伴流的不均匀程度。 WOF值越小，说明伴流场越均匀，其表达如下：
{WOF = \frac{{\displaystyle\sum\limits_{r = {R_{\rm{hub}}}}^{{R_r}} {\sigma _{\rm{W}}^r} }}{{\displaystyle\sum\limits_{r = {R_{\rm{hub}}}}^{{R_r}} {\mu _{\rm{W}}^r} }}} (5) {W_{\text{axial}}\left( {r,\alpha } \right) = 1 - \frac{{V_{\text{axial}}}}{{{V_0}}}} (6) {\mu _{\rm{W}}^r = \frac{1}{n}\sum\limits_{\varphi = {0^ \circ }}^{{{360}^ \circ }} {{W_{\rm{axial}}}(r,\alpha )} } (7) {\sigma _{\rm{W}}^r = \sqrt {\frac{1}{n}\sum\limits_{\varphi = {0^ \circ }}^{{{360}^ \circ }} {{{\left( {W_{\text{axial}}\left( {r,\alpha } \right) - \mu _{\rm{W}}^r} \right)}^2}} } } (8) 式中：{R_r}，{R_{{\text{hub}}}}分别为桨盘面半径和轮毂半径；\sigma _{\rm{W}}^r为桨盘面某个半径处的轴向伴流分数标准差；W_{\text{axial}}为轴向伴流分数； {\mu }_{\rm{W}}^{r} 为桨盘面某个半径处轴向伴流分数均值；n为桨盘面某个半径处轴向伴流分数的取值点数目。
2.2 尾翼轴向位置对伴流场的影响
如图5所示，流体流过尾翼后会形成梢涡和马蹄涡，对流场产生扰动，从而影响流场的轴向速度发展趋势。涡团沿着给定去流角的艇尾结构向下游发展时，会形成不均匀的低速尾流，与周围流体产生明显的速度差。此外，马蹄涡在桨盘面位置发生汇聚，将进一步加剧桨盘面轴向速度的不均匀性。
给定远场来流V0 = 3.051 m/s，为了探究尾翼轴向位置h对伴流场的影响，分别在去流角θ = 10°和20°时，比较尾翼轴向位置h = 3.810 0，3.962 4和4.114 8 m时的伴流场特性。
表2统计了不同尾翼轴向位置的伴流场WOF值。从中可以发现，当去流角θ = 10°时，随着尾翼轴向位置增大，桨盘面伴流场的WOF值逐渐降低，即不均匀度逐渐减小。当去流角θ = 20°时，随着尾翼轴向位置的增大，WOF先降低后增大，伴流场不均匀度先减小后增加。此外，当去流角θ = 20°时，伴流场的不均度整体较大，受尾翼轴向位置变化的影响较小。这是因为Suboff模型在参数化建模过程中固定了尾翼迎流面积，随着尾翼轴向位置的增大，尾翼高度逐渐降低，对主流的扰动区域减小，马蹄涡发展耗散距离减小，进而对桨盘面位置流场的干扰程度产生不同影响。变化去流角θ时，尾翼高度相应发生变化，复杂的分离涡流动在向下游桨盘面发展的过程也会受到几何结构的影响，进而影响伴流场的均匀性。
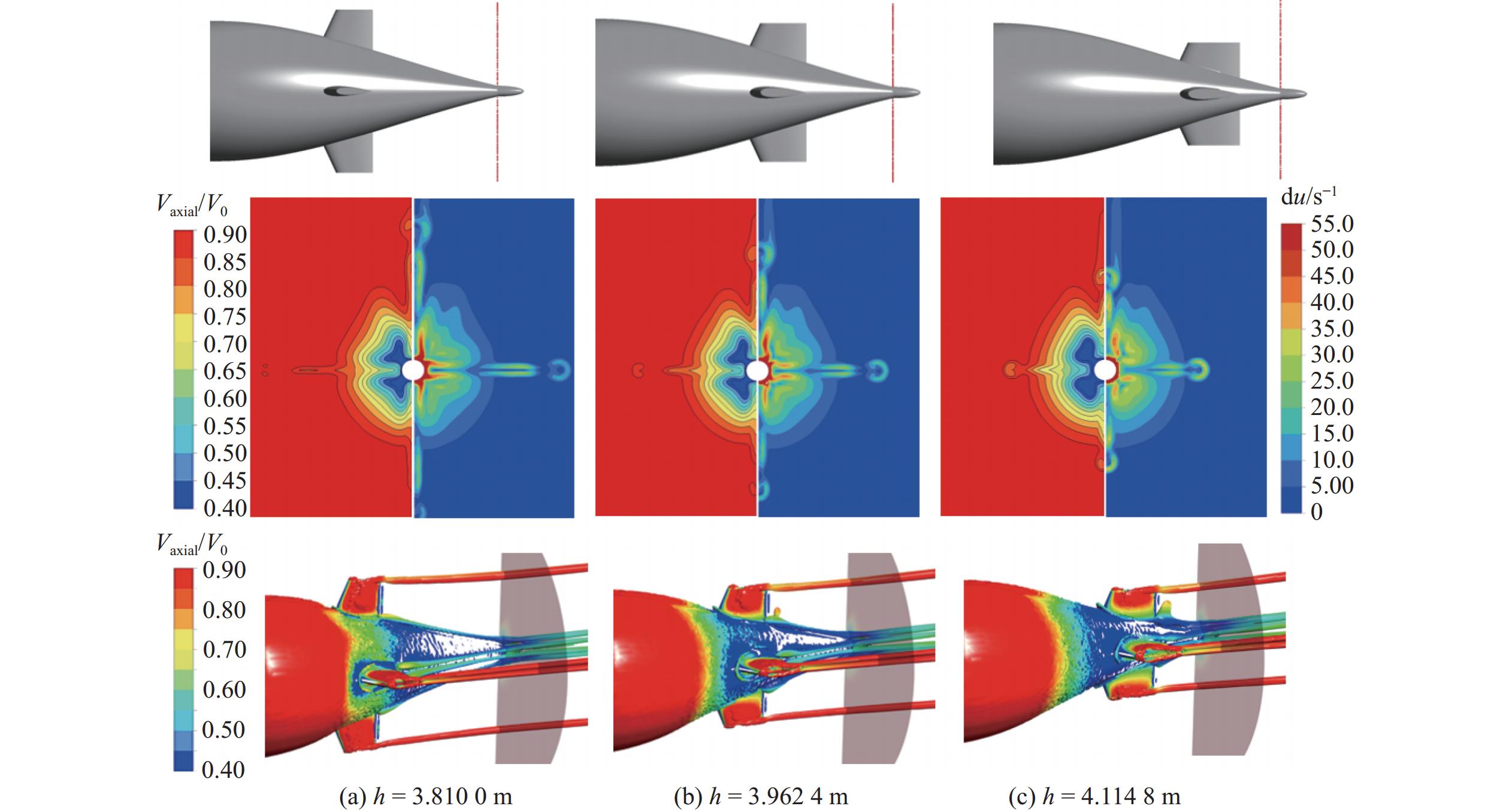
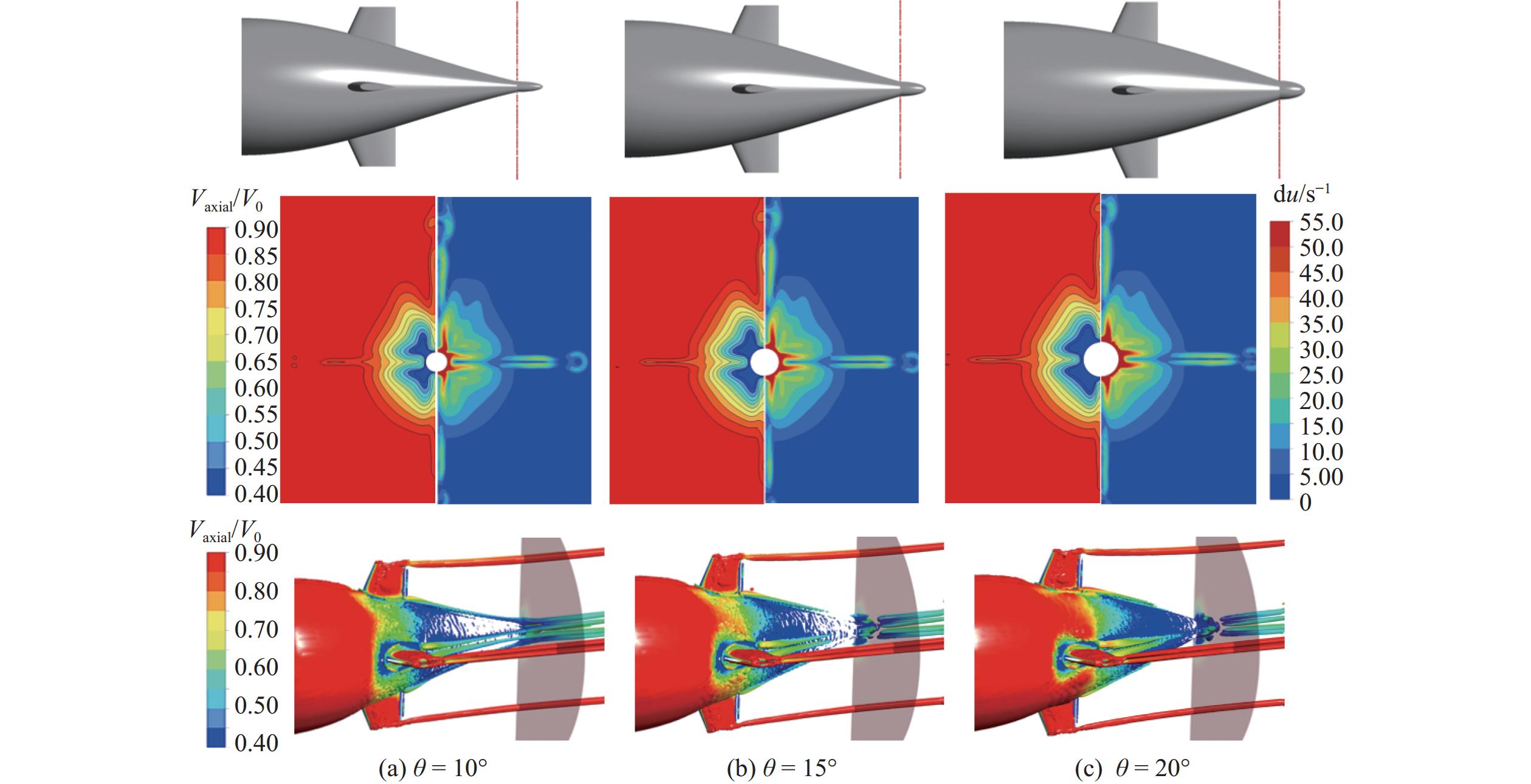
表 2 不同尾翼轴向位置下桨盘面伴流场WOF值Table 2. The WOF values of wake filed at the propeller disk under different tail fin axial positions去流角θ/(°) WOF值 h = 3.810 0 m h = 3.962 4 m h = 4.114 8 m 10 0.124 5 0.115 3 0.091 4 20 0.104 9 0.114 5 0.106 8 图7所示为去流角θ = 10°时，3种尾翼轴向位置对应的航行体尾部结构几何示意图（上）、桨盘面无因次轴向速度等值线云图和轴向速度梯度du等值线云图（中）以及航行体尾部涡量Q = 10 s−2时涡核区域无因次轴向速度等值线云图（下）。
![]()
图 7 θ = 10°时尾翼轴向位置对桨盘面伴流场的影响Figure 7. The influence of tail fin axial position on the wake field at the propeller disk under the angle of run of the stern θ = 10°由图7可以看出，在附体马蹄涡和梢涡的共同作用下，桨盘面位置形成了明显的不均匀低速区，存在较大的轴向速度梯度，并且在速度变化曲线中形成了对应的峰谷值。随着尾翼轴向位置的增大，尾翼的高度逐渐降低，涡团强度和涡团的输运扰动程度受到影响。当去流角θ = 10°时，表现为桨盘面低速范围变大，但速度等值线的弯曲程度却在降低，对应的速度梯度也在减小，涡团输运耗散距离减小，在桨盘面位置产生了更大的低速区域。但涡核区域的速度梯度较小，壁面附近的速度场会更加均匀，使得WOF中的伴流分数均值增大而标准差减小，最终整体表现为WOF值减小，桨盘面伴流场的不均匀程度降低。
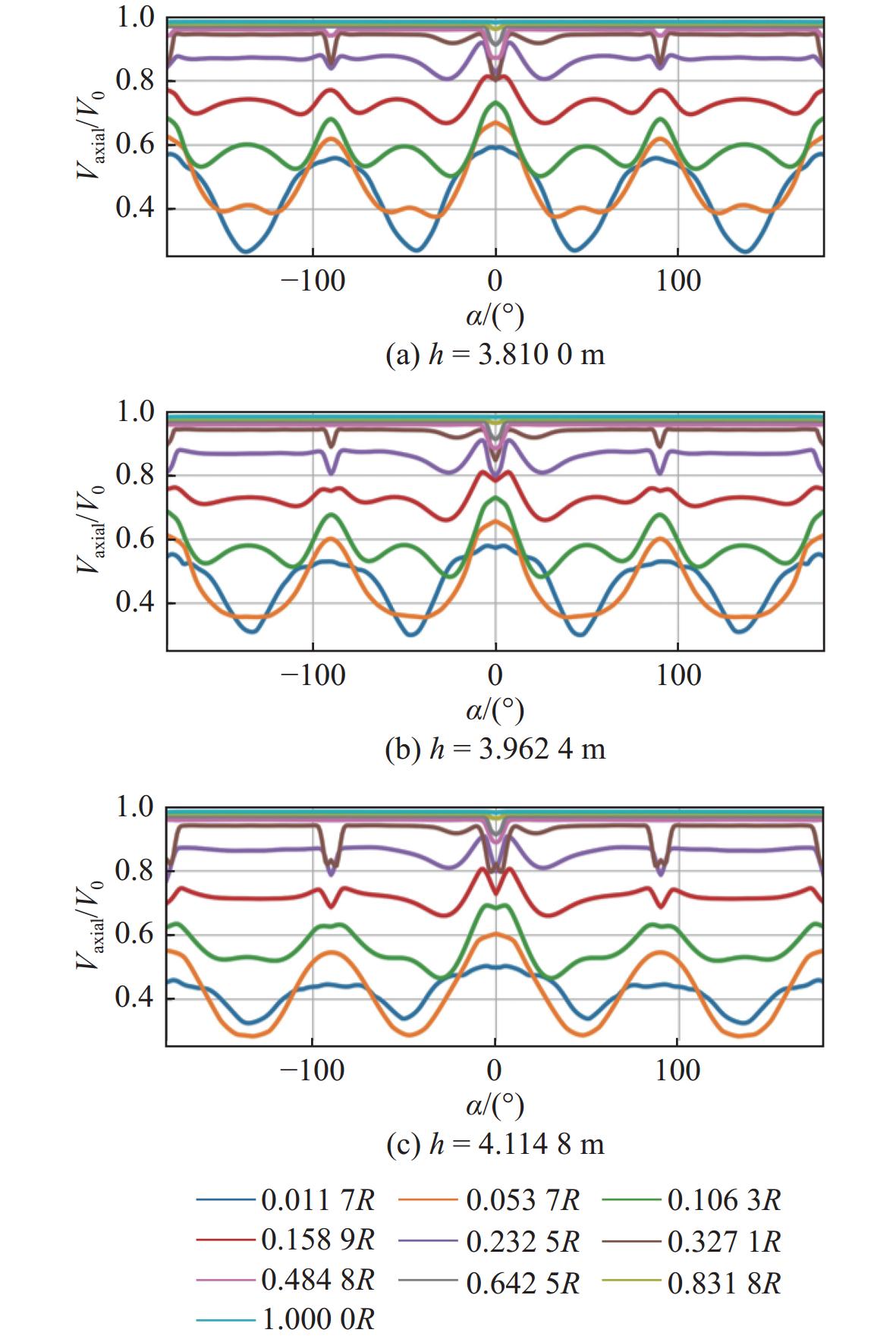
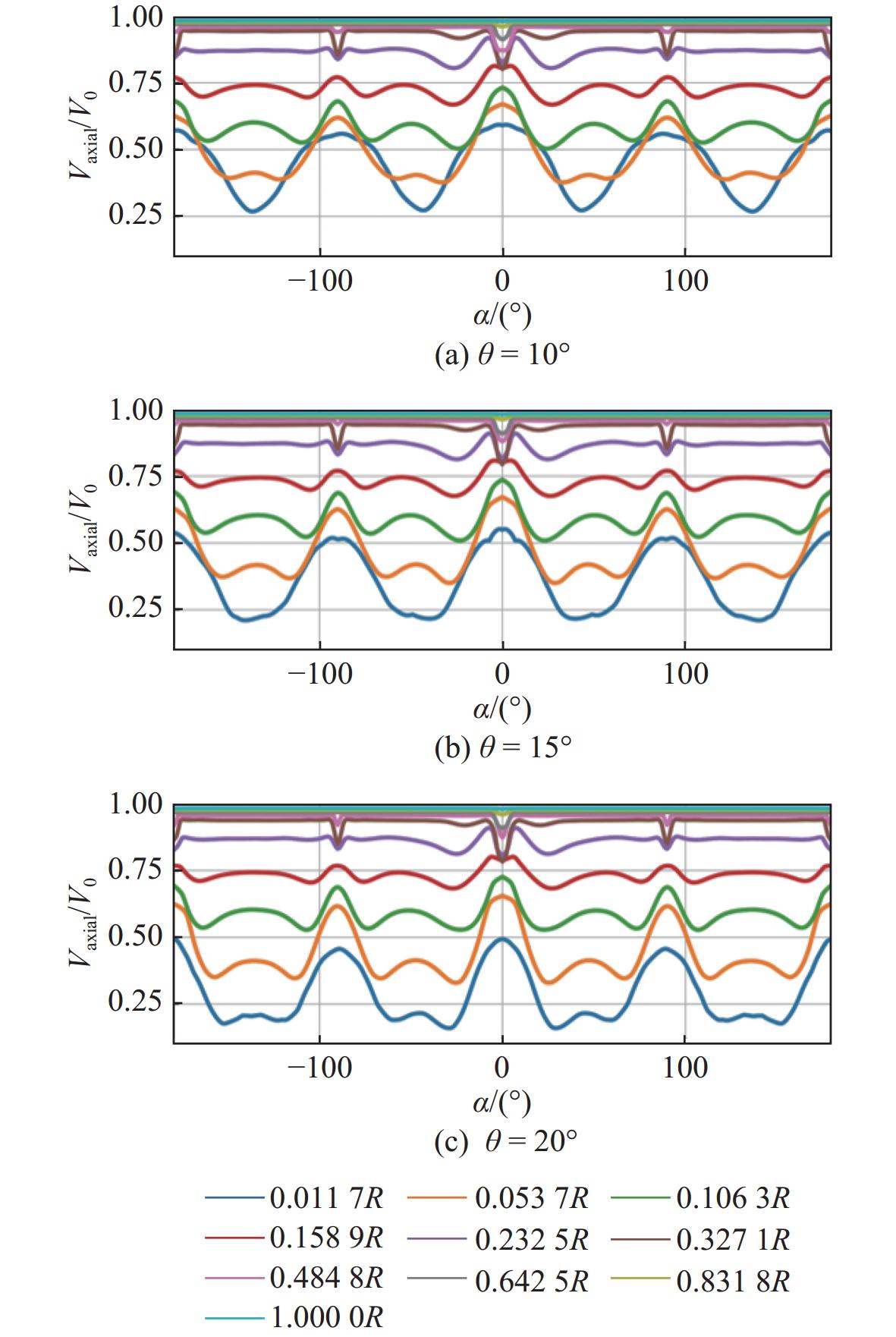
图8所示为桨盘面无因次轴向速度随周向角α的变化曲线，其中R为桨盘面半径Rr与轮毂半径Rhub的差值。从中可以直观地看到，随着尾翼轴向位置的增大，靠近轮毂位置半径处的无因次轴向速度值降低，峰谷值也逐渐降低，使得速度标准差降低，表现为圆周上无因次轴向速度空间波动减小，伴流场均匀性提升。
![]()
图 8 θ = 10°时尾翼轴向位置对桨盘面无因次轴向速度的影响Figure 8. The influence of tail fin axial position on the normalized axial velocity at the propeller disk under the angle of run of the stern θ = 10°图9所示为去流角θ = 20°时3种尾翼轴向位置对伴流场的影响。与图7有所区别，此时随着尾翼轴向位置的增大，桨盘面低速区范围变化不大，速度梯度呈现先增大后减小的细微变化趋势，涡核区域变化较小，使得WOF值是先增大后减小，桨盘面伴流场的不均匀程度是先升高后略微降低。
![]()
图 9 θ = 20°时尾翼轴向位置对桨盘面伴流场的影响Figure 9. The influence of tail fin axial position on the wake field at the propeller disk under the angle of run of the stern θ = 20°图10所示为无因次轴向速度变化曲线。从中可以看到，当去流角θ = 20°时，随着尾翼轴向位置的增大，靠近轮毂位置半径处的无因次轴向速度值略微降低，速度标准差是先增大再减小，但变化幅度较小，对伴流场均匀性的影响较小。
![]()
图 10 θ = 20°时尾翼轴向位置对桨盘面无因次轴向速度的影响Figure 10. The influence of tail fin axial position on the normalized axial velocity at the propeller disk under the angle of run of the stern θ = 20°2.3 去流角对桨盘面伴流场的影响
上述结果表明，去流角也会显著影响Suboff模型尾部涡团的流动发展。因此，为了探究去流角对伴流场的影响，分别在尾翼轴向位置h = 3.810 0和4.114 8 m时比较了去流角θ = 10°，15°和20°时不同Suboff模型尾部结构下的伴流场特性。
表3统计了不同去流角下的伴流场WOF值。从中可以发现，当尾翼轴向位置h = 3.810 0 m时，随着去流角的增大，桨盘面伴流场的WOF值逐渐降低，伴流场不均匀度逐渐减小；当尾翼轴向位置h = 4.114 8 m时，随着去流角的增大，WOF值逐渐增大，伴流场不均匀度逐渐增加。同样，由于固定了尾翼迎流面积，当尾翼轴向位置较大时，尾翼高度较低，对主流的扰动会减小，且马蹄涡发展耗散距离也减小，进而对桨盘面处流场的干扰程度产生影响。因此，较小的尾翼轴向位置所对应的WOF值整体偏大。
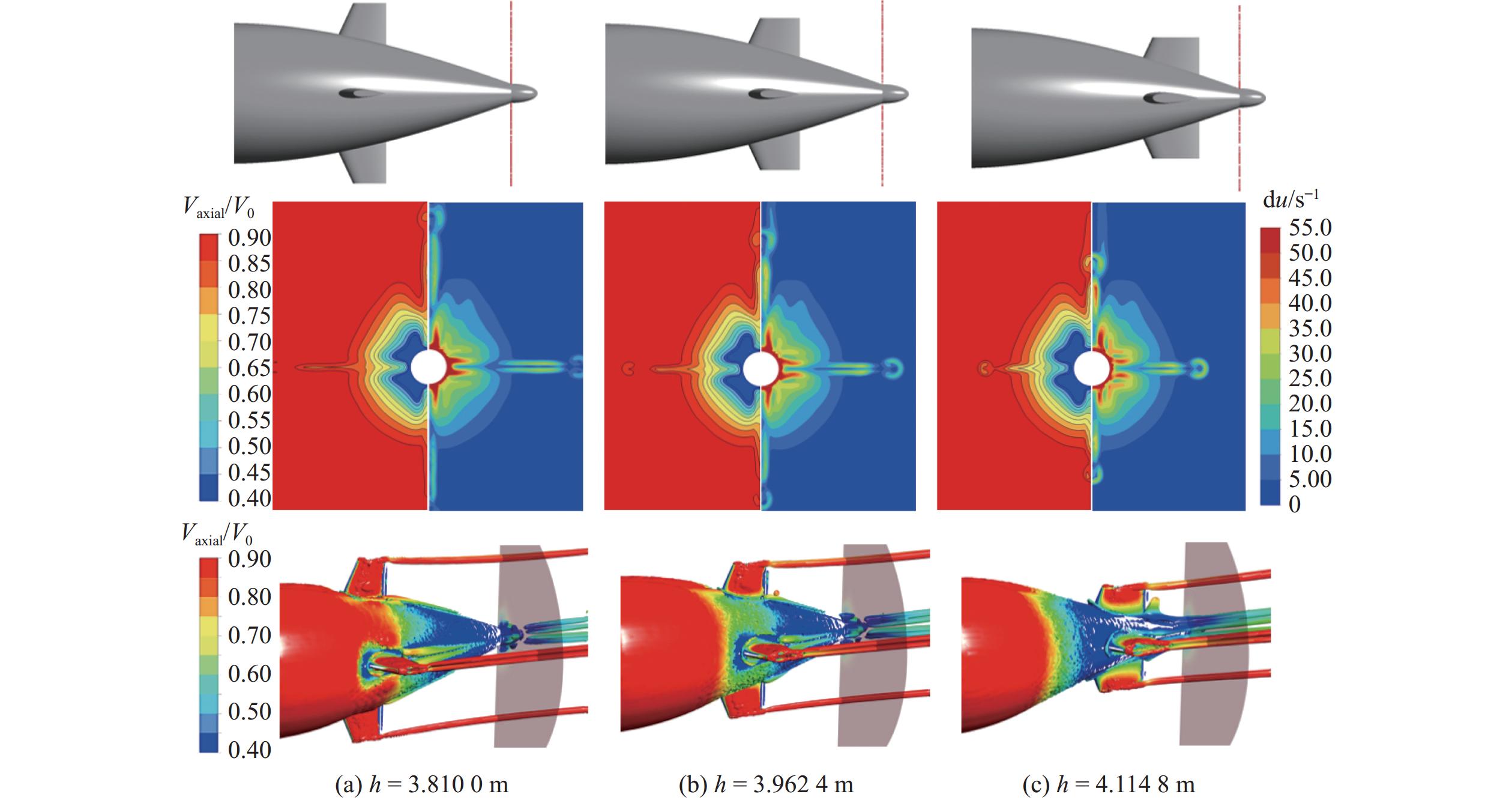
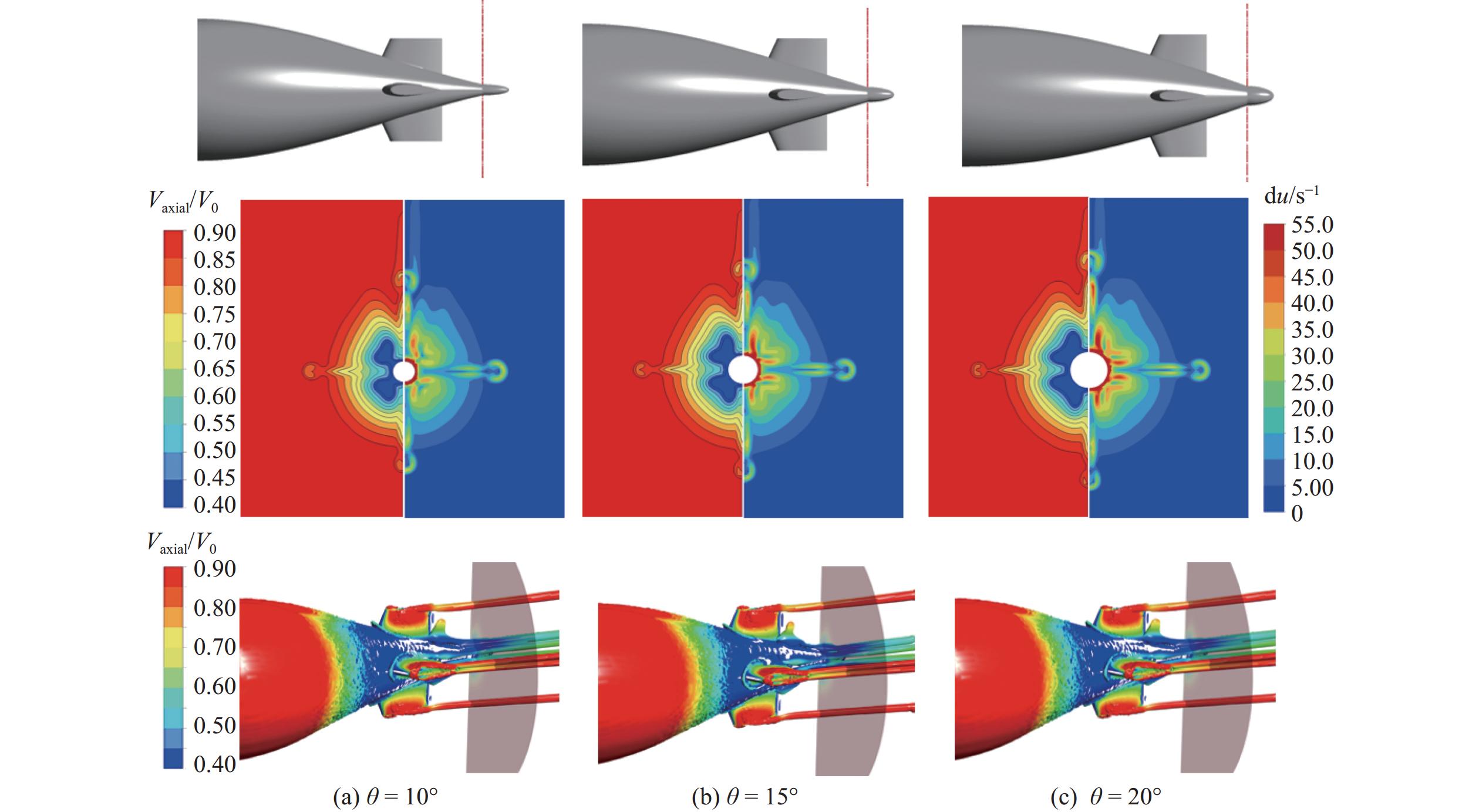
表 3 不同去流角下桨盘面伴流场WOF值Table 3. The WOF values of wake field at the propeller disk under different angle of run of the stern尾翼位置h/m WOF值 θ = 10° θ = 15° θ = 20° 3.810 0 0.124 5 0.117 1 0.104 9 4.114 8 0.091 4 0.099 6 0.106 8 图11所示为尾翼轴向位置h = 3.810 0 m时3种Suboff模型尾部去流角对伴流场的影响。从中可以观察到，随着去流角的增大，桨盘面低速范围明显增大，速度梯度变化不明显；较大的去流角在桨盘面位置处会形成面积更大的低速涡核区域；靠近壁面的速度场更加均匀，使得WOF值逐渐减小，桨盘面伴流场的不均匀程度降低。
![]()
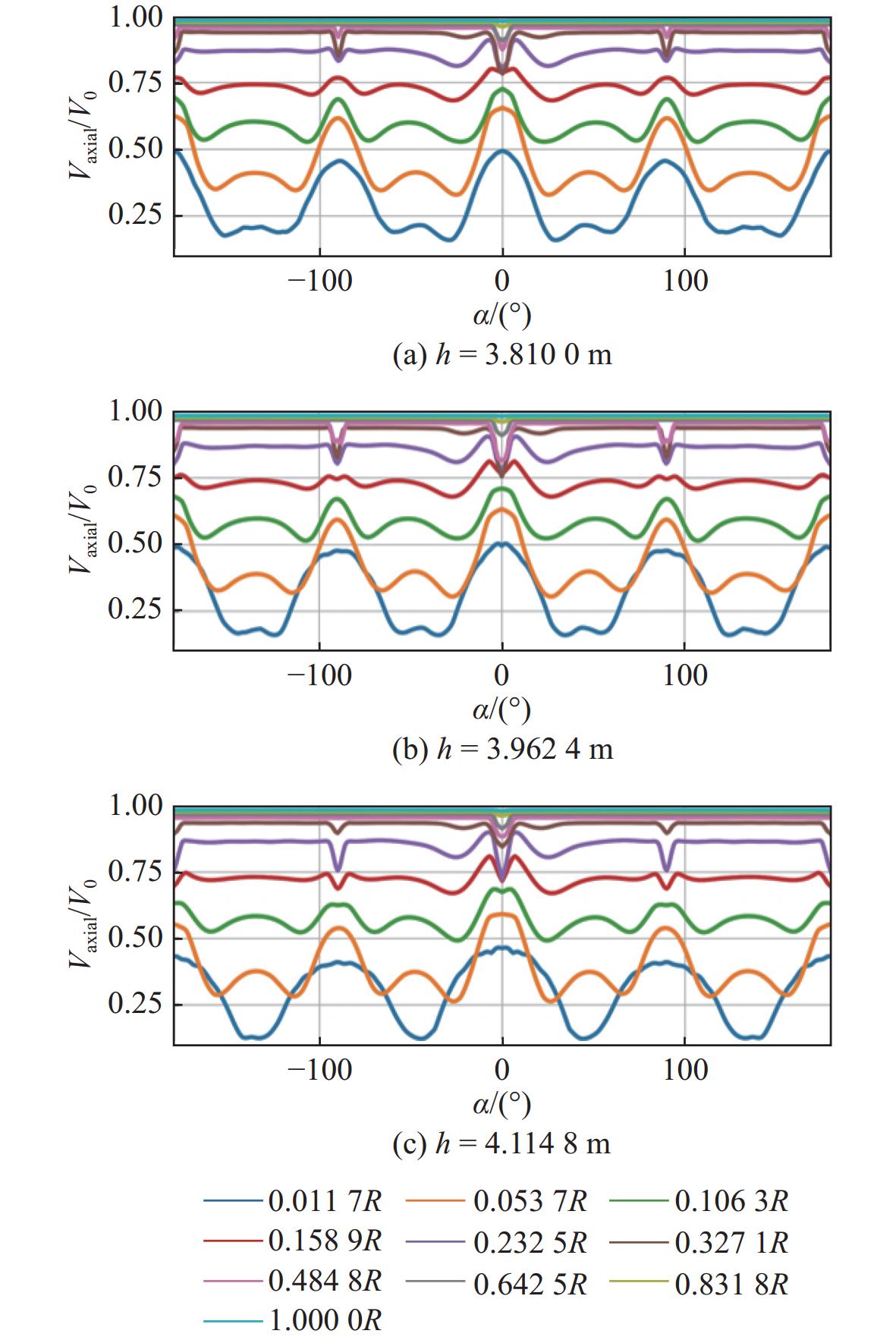
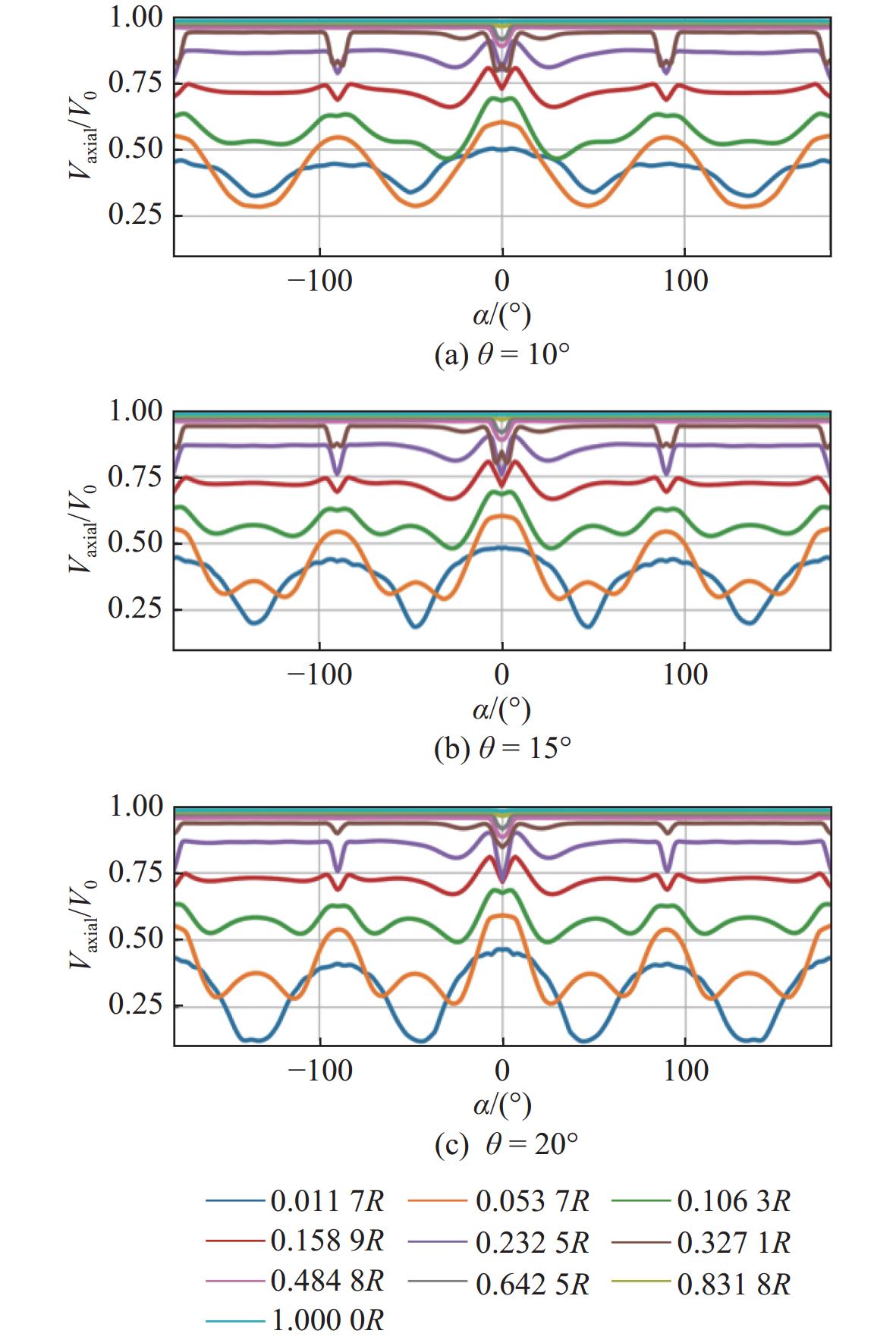
图 11 h = 3.810 0 m时去流角对桨盘面伴流场的影响Figure 11. The influence of the angle of run of the stern on the wake field at the propeller disk under the tail fin axial position h = 3.810 0 m图12所示为h = 3.810 0 m时桨盘面无因次轴向速度变化曲线。从中可以看到，随着去流角的增大，靠近轮毂位置半径处的无因次轴向速度值明显降低，峰谷值则略微降低，速度标准差略有降低，但变化幅度较小，最终使得伴流场均匀性提升。当尾翼位置h = 3.810 0 m时，尾翼高度较大，对主流扰动明显，并且足够的轴向位置使得涡团在输运过程中对流场产生充分的扰动，速度梯度整体较大，WOF值偏大，伴流场不均匀性高。
![]()
图 12 h = 3.810 0 m时去流角对桨盘面无因次轴向速度的影响Figure 12. The influence of the angle of run of the stern on the normalized axial velocity at the propeller disk under the tail fin axial position h = 3.810 0 m图13所示为尾翼轴向位置h = 4.114 8 m时3种Suboff模型尾部去流角对伴流场的影响。与图11不同，随着去流角的增大，桨盘面低速范围明显增大，速度梯度同样增大较明显，在综合作用下，WOF值呈略微增大的趋势，桨盘面伴流场的不均匀程度增大。
![]()
图 13 h = 4.114 8 m时去流角对桨盘面伴流场的影响Figure 13. The influence of the angle of run of the stern on the wake field at the propeller disk under the tail fin axial position h = 4.114 8 m图14所示为h = 4.114 8 m时桨盘面无因次轴向速度变化曲线。从中可以看到，随着去流角的增大，靠近轮毂位置半径处的无因次轴向速度值明显降低，峰谷值逐渐增大，速度标准差增大，最终使得伴流场均匀性降低。
![]()
图 14 h = 4.114 8 m时去流角对桨盘面无因次轴向速度的影响Figure 14. The influence of the angle of run of the stern on the normalized axial velocity at the propeller disk under the tail fin axial position h = 4.114 8 m3. 设计范围内尾部参数对伴流品质的灵敏度分析
3.1 设计范围内尾部几何结构对伴流场品质的响应分析
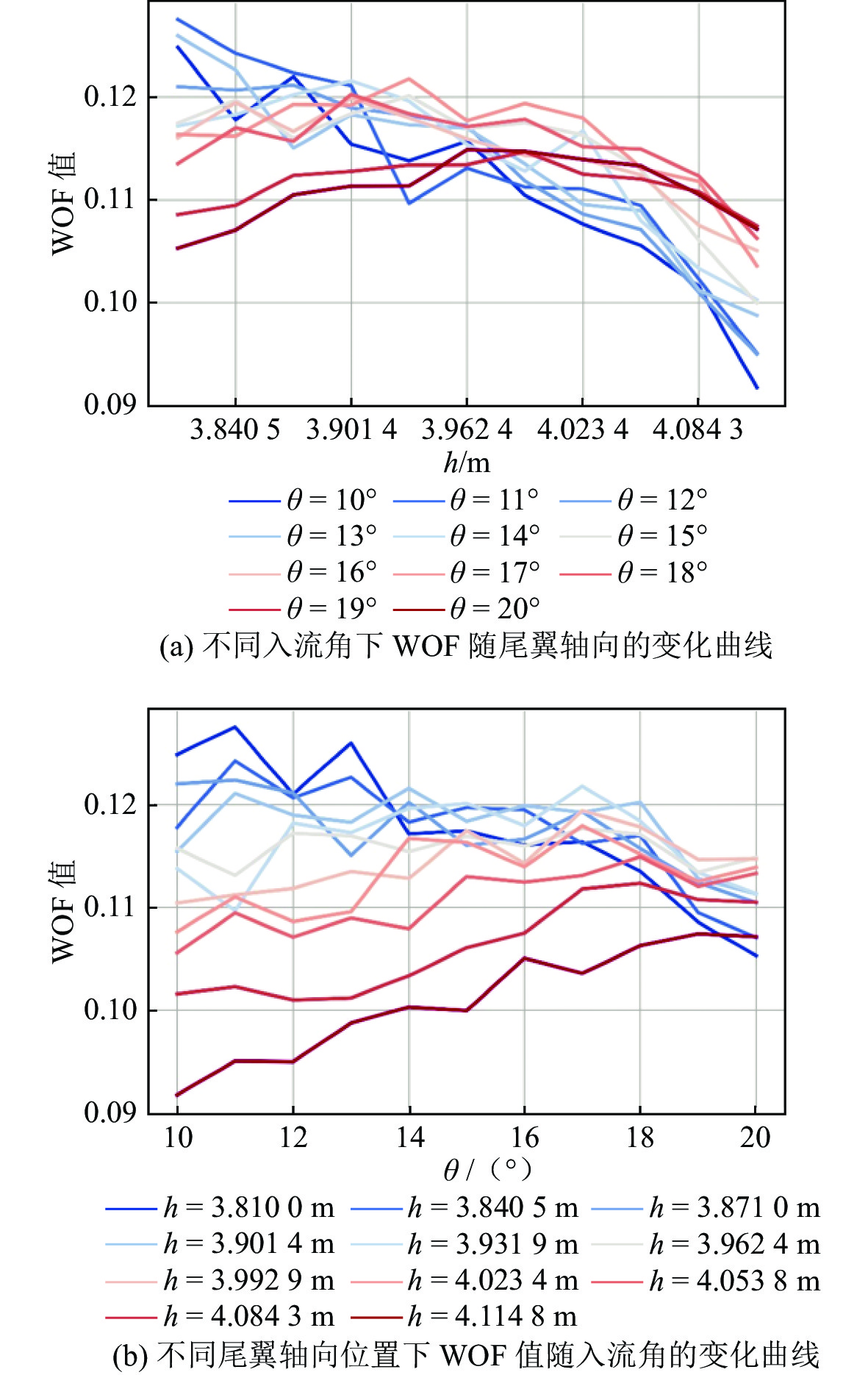
为进一步全面探讨去流角θ和尾翼轴向位置h与伴流场WOF值之间的响应关系，令去流角θ从10°增大到20°，样本间隔为1°，尾翼位置h从3.810 0 m增大到4.114 8 m，样本间隔为0.304 8 m，在设计范围内一共生成121个仿真样本。图15所示为121个样本所对应的不同Suboff模型尾部几何参数的WOF曲线图。
![]()
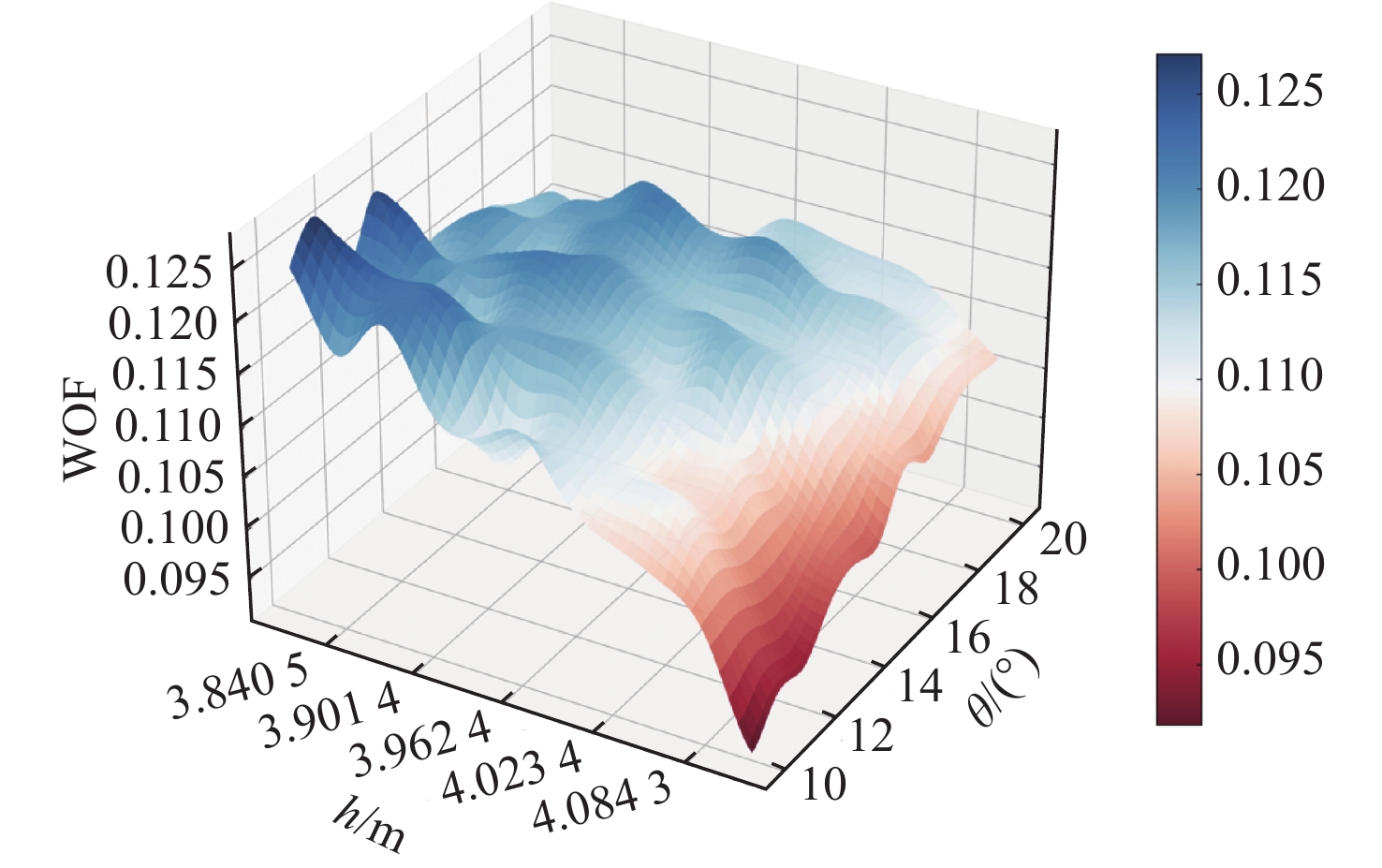
图 15 不同入流角下WOF值随尾翼轴向的变化曲线及不同尾翼轴向位置下WOF值随入流角的变化曲线Figure 15. The WOF variation curves with the tail fin axial position at different angle of run of the stern and the WOF variation curves with the angle of run of the stern at different tail fin axial positions由图15（a）可以看到，在去流角较小时，随着尾翼轴向位置的增大，WOF值呈递减趋势；而当去流角逐渐增大后，该趋势逐渐趋于平缓，最终转变为先递增再递减的变化趋势。此外，WOF最小值对应去流角最小、尾翼轴向位置最大的Suboff模型尾部结构。由图15（b）可以看到，当尾翼轴向位置较小时，随着去流角的增大，WOF值呈递减趋势，而当尾翼轴向位置逐渐增大后，该趋势逐渐趋于平缓，最终转变为递增的变化趋势。此外，较小的去流角对尾翼轴向位置的变化更加敏感。
特别地，将θ = 10°，h = 4.114 8 m时的最优样本与原始Suboff模型的伴流场进行对比，结果如图16所示。由图可见，原始Suboff模型尾翼与桨盘面间的轴向距离较大，尾翼区域涡量Q = 10 s−2的涡核面积更大；同时，相邻尾翼产生的马蹄涡发生融合的位置距桨盘面较远。在红色虚线表示的桨盘面归一化轴向速度场和黑色虚线表示的水平面归一化轴向速度场中可以看到，最优尾部结构的桨盘面涡核区域速度场明显降低，等值线的弯曲程度减弱。最优尾部结构对应的WOF值为0.091 4，相比原始Suboff模型，降低了14.66%，有效提升了桨盘面伴流场的均匀性。
![]()
图 16 原始Suboff模型及最优Suboff模型尾部伴流场云图Figure 16. Wake field contours of the original Suboff model and the optimal Suboff model3.2 基于高斯过程的尾部几何结构对伴流场品质的灵敏度分析
由3.1节可知，Suboff模型尾部结构对伴流场的影响规律并未呈现单调相关性。基于此，将通过构建代理模型来反应设计空间中Suboff模型尾部结构与WOF的响应关系，为Suboff模型尾部结构设计提供参考。本文采用高斯过程（Gaussian process, GP）代理模型描述数据的先验信念和似然分布[26]。通过水下航行体尾部结构数据和伴流场性能指标数据，建立已知点与未知点之间的联系，实现对整个设计空间带不确定性衡量的性能预测。
将121个样本随机划分为109个训练样本和12个测试样本，进行高斯过程预测精度验证。使用决定系数R2和均方根误差RMSE评估模型的拟合精度，其表达式如下：
{R}^{2}=1-\frac{{{\displaystyle {\displaystyle \sum _{i=1}^{p}{({f}_{i}\left(x\right)-{\hat{f}_{i}}\left(x\right))}^{2}}}}}{{{\displaystyle {\displaystyle \sum _{i=1}^{p}{({f}_{i}\left(x\right)-{\bar{f}_{i}}\left(x\right))}^{2}}}}} (9) {RMSE = \sqrt {\frac{1}{p} \sum \limits_{i = 1}^p {{({f_i}\left( x \right) - {{\hat f_i}}\left( x \right))}^2}} } (10) 式中： {{\hat f_i}}\left( x \right) 为测试集上的高斯过程模型预测结果； {{\bar f_i}} \left( x \right)为测试集真实结果{f_i}\left( x \right)的平均值；p为测试集样本个数。最终，在12个测试集上，高斯过程模型的R2 = 0.946 7，均方根误差RMSE = 0.001 577，表明高斯过程模型能够准确反映WOF与尾部去流角和尾翼轴向位置之间的映射关系。
为进一步量化尾部参数对伴流场WOF的敏感性，根据121个样本构建了高斯过程响应面，这样一方面可以更加直观地看到整个设计空间内的WOF分布（图17），另一方面可以基于该响应面度量参数敏感性。
![]()
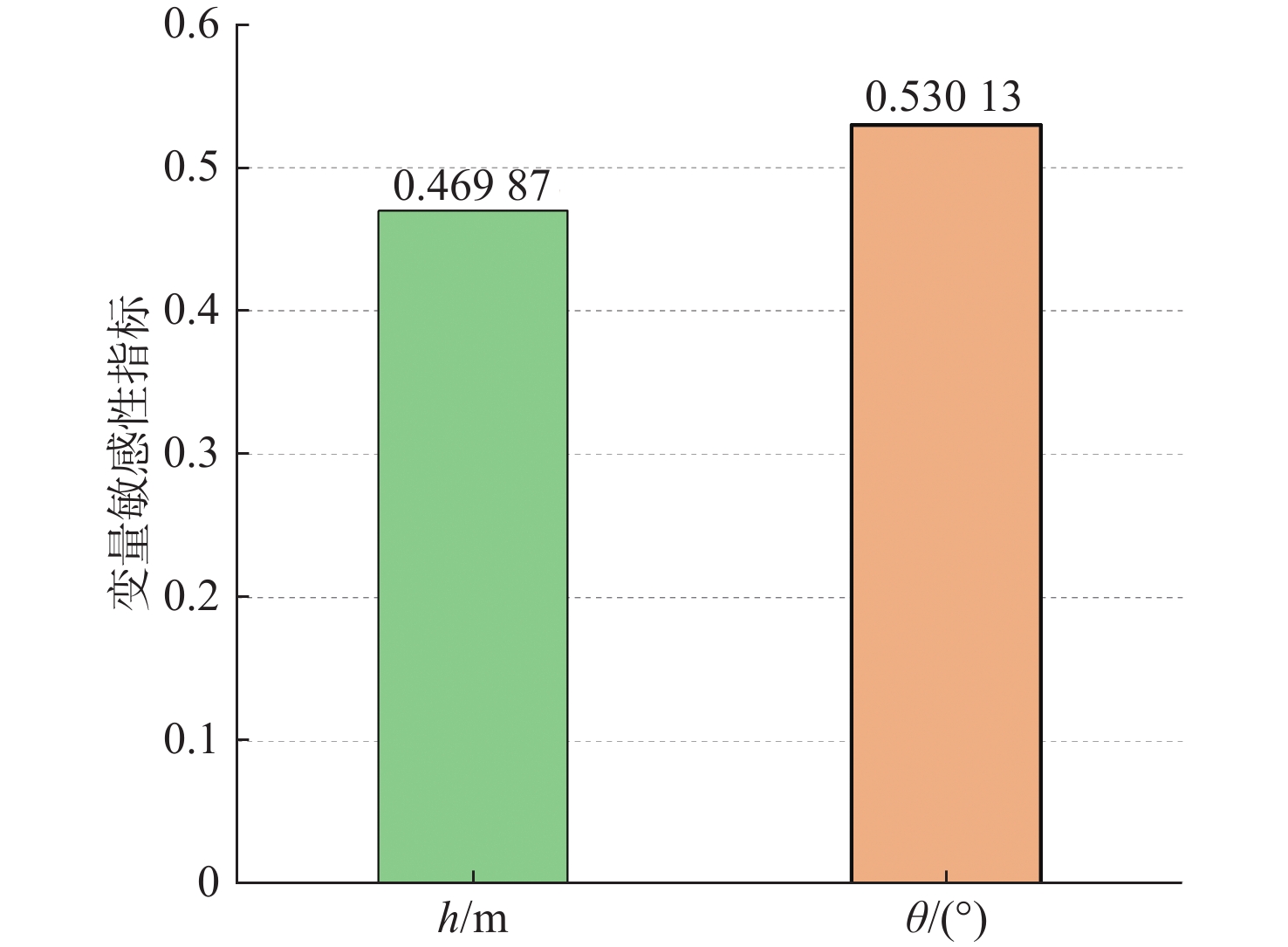
图 17 尾翼轴向位置和尾部去流角与WOF的高斯过程响应面Figure 17. The Gaussian process response surface of WOF with respect to the axial tail fin axial position and the angle of run of the stern首先，对于采用自动相关性确认（automatic relevance determination，ARD）形式核函数的高斯过程模型而言，其核函数沿各输入维度的输入尺度参数li代表了结果响应在该维度方向的变化速度，反映了模型对输入的敏感性。较大的li表示模型对输入的变化不敏感，更关注整体趋势；较小的li则表示模型对输入的变化敏感，更加关注局部细节。将输入尺度参数的倒数归一化 \dfrac{{{1 /{l_i}}}}{{\sum\limits_{i = 1}^k {(1/{l_i})} }} 作为衡量模型对变量的全局敏感性指标，其中k为输入变量维度。如图18所示，尾翼轴向位置归一化全局敏感性指标为0.469 87，尾部去流角的归一化全局敏感性为0.530 13，表明WOF对尾部去流角的变化更加敏感。
![]()
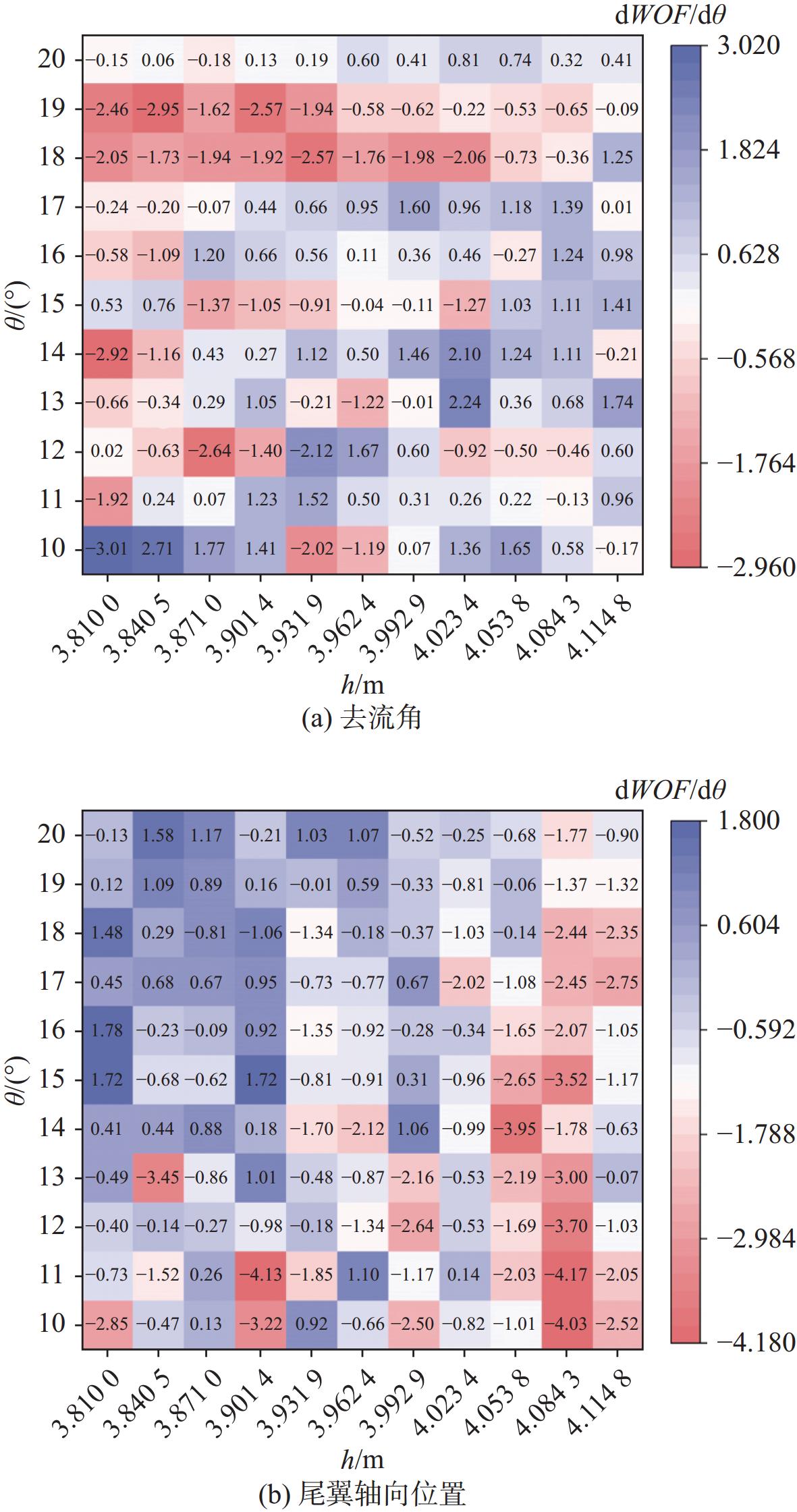
图 18 尾翼轴向位置和尾部去流角的全局敏感性指标Figure 18. The global sensitivity indicators of the axial tail fin axial position and the angle of run of the stern进一步地，通过训练后的高斯过程模型在各个位置的偏导数信息，可以评估WOF对输入变量在特定位置微小摄动的局部敏感程度。偏导数的绝对值较大表示函数对该变量的变动更为敏感，偏导数的绝对值较小则表示函数对该变量的变动不太敏感。如图19（a）所示，对于去流角，WOF在θ = 10°，18°和19°时局部敏感性较大，特别是在轴向位置h = 3.810 0和3.840 5 m位置处。如图19（b）所示，对于尾翼轴向位置，WOF在h = 4.084 3 m时局部敏感性较大，特别是在去流角较小位置处。
![]()
图 19 去流角及尾翼轴向位置局部敏感性分析Figure 19. The local sensitivity of the angle of run of the stern and the tail fin axial position4. 结 论
本文通过对Suboff艇体尾部参数化数值模拟，探究了尾翼迎流面积不变时尾翼轴向位置和尾部去流角对桨盘面伴流场品质的影响规律，主要得到如下结论：
1） 流体经过艇体尾翼会形成明显的涡团，对流场产生扰动，影响流场的轴向速度发展趋势。当去流角θ = 10°时，随着尾翼轴向位置的增大，桨盘面伴流场的WOF值逐渐降低，伴流场不均匀度逐渐减小；但当去流角θ = 20°时，随着尾翼轴向位置的增大，WOF值先降低后增大，伴流场不均匀度先减小再增加。
2） 流体涡团将沿给定去流角的艇尾结构向后发展，形成不均匀的低速尾流。当尾翼轴向位置h = 3.810 0 m时，随着去流角的增大，桨盘面伴流场的WOF值逐渐降低，伴流场不均匀度逐渐减小；但当尾翼轴向位置h = 4.114 8 m时，随着去流角的增大，WOF值逐渐增大，伴流场不均匀度逐渐增加。
3） 构建尾部几何参数与WOF之间的响应关系，进行敏感性分析。其中全局敏感性分析结果表明，设计空间内WOF值对尾部去流角的全局变化更加敏感；局部敏感性分析结果表明，对于去流角，WOF在去流角较大和较小时均比较敏感，特别是在尾翼轴向位置较小处；对于尾翼轴向位置，WOF在轴向位置较大时比较敏感，特别是在去流角较小处。
-
![]()
图 1 Suboff参数化建模及固定尾翼迎流面积时尾部参数变化示意图
Figure 1. Suboff parametric modeling and the variation in tail parameters when the tail fin upwind area is fixed
![]()
图 3 Suboff模型计算域及边界条件
Figure 3. The computational domain and boundary conditions of Suboff model
![]()
图 4 Suboff模型计算域非结构网格
Figure 4. Unstructured grids for the computational domains of Suboff model
![]()
图 6 桨盘面无因次轴向速度对比
Figure 6. Comparison of the normalized axial velocity on the propeller disk surface
![]()
图 7 θ = 10°时尾翼轴向位置对桨盘面伴流场的影响
Figure 7. The influence of tail fin axial position on the wake field at the propeller disk under the angle of run of the stern θ = 10°
![]()
图 8 θ = 10°时尾翼轴向位置对桨盘面无因次轴向速度的影响
Figure 8. The influence of tail fin axial position on the normalized axial velocity at the propeller disk under the angle of run of the stern θ = 10°
![]()
图 9 θ = 20°时尾翼轴向位置对桨盘面伴流场的影响
Figure 9. The influence of tail fin axial position on the wake field at the propeller disk under the angle of run of the stern θ = 20°
![]()
图 10 θ = 20°时尾翼轴向位置对桨盘面无因次轴向速度的影响
Figure 10. The influence of tail fin axial position on the normalized axial velocity at the propeller disk under the angle of run of the stern θ = 20°
![]()
图 11 h = 3.810 0 m时去流角对桨盘面伴流场的影响
Figure 11. The influence of the angle of run of the stern on the wake field at the propeller disk under the tail fin axial position h = 3.810 0 m
![]()
图 12 h = 3.810 0 m时去流角对桨盘面无因次轴向速度的影响
Figure 12. The influence of the angle of run of the stern on the normalized axial velocity at the propeller disk under the tail fin axial position h = 3.810 0 m
![]()
图 13 h = 4.114 8 m时去流角对桨盘面伴流场的影响
Figure 13. The influence of the angle of run of the stern on the wake field at the propeller disk under the tail fin axial position h = 4.114 8 m
![]()
图 14 h = 4.114 8 m时去流角对桨盘面无因次轴向速度的影响
Figure 14. The influence of the angle of run of the stern on the normalized axial velocity at the propeller disk under the tail fin axial position h = 4.114 8 m
![]()
图 15 不同入流角下WOF值随尾翼轴向的变化曲线及不同尾翼轴向位置下WOF值随入流角的变化曲线
Figure 15. The WOF variation curves with the tail fin axial position at different angle of run of the stern and the WOF variation curves with the angle of run of the stern at different tail fin axial positions
![]()
图 16 原始Suboff模型及最优Suboff模型尾部伴流场云图
Figure 16. Wake field contours of the original Suboff model and the optimal Suboff model
![]()
图 17 尾翼轴向位置和尾部去流角与WOF的高斯过程响应面
Figure 17. The Gaussian process response surface of WOF with respect to the axial tail fin axial position and the angle of run of the stern
![]()
图 18 尾翼轴向位置和尾部去流角的全局敏感性指标
Figure 18. The global sensitivity indicators of the axial tail fin axial position and the angle of run of the stern
![]()
图 19 去流角及尾翼轴向位置局部敏感性分析
Figure 19. The local sensitivity of the angle of run of the stern and the tail fin axial position
表 1 Suboff模型阻力及误差
Table 1 The resistance values and errors for the Suboff model
网格数量 阻力/N 相对误差/% 实验 仿真 5.279×106 102.3 95.475 6.672 10.861×106 102.3 99.351 2.882 20.122×106 102.3 101.233 1.043 
下载: 导出CSV
表 2 不同尾翼轴向位置下桨盘面伴流场WOF值
Table 2 The WOF values of wake filed at the propeller disk under different tail fin axial positions
去流角θ/(°) WOF值 h = 3.810 0 m h = 3.962 4 m h = 4.114 8 m 10 0.124 5 0.115 3 0.091 4 20 0.104 9 0.114 5 0.106 8
下载: 导出CSV
表 3 不同去流角下桨盘面伴流场WOF值
Table 3 The WOF values of wake field at the propeller disk under different angle of run of the stern
尾翼位置h/m WOF值 θ = 10° θ = 15° θ = 20° 3.810 0 0.124 5 0.117 1 0.104 9 4.114 8 0.091 4 0.099 6 0.106 8
下载: 导出CSV
-
[1] BENNAYA M, ZHANG W P, HEGAZE M M. Estimation of the induced hydrodynamic periodic forces of marine propeller under non-uniform inflow via CFD[J]. Applied Mechanics and Materials, 2013, 467: 293–299. doi: 10.4028/www.scientific.net/AMM.467.293
[2] LIN Y H, LI X C. The investigation of a sliding mesh model for hydrodynamic analysis of a SUBOFF model in turbulent flow fields[J]. Journal of Marine Science and Engineering, 2020, 8(10): 744. doi: 10.3390/jmse8100744
[3] ASHOK A, VAN BUREN T, SMITS A J. The structure of the wake generated by a submarine model in yaw[J]. Experiments in Fluids, 2015, 56(6): 123. doi: 10.1007/s00348-015-1997-4
[4] HUANG T, LIU H L. Measurements of flows over an axisymmetric body with various appendages in a wind tunnel: the DARPA SUBOFF experimental program[C]//Proceedings of 19th Symposium on Naval Hydrodynamics. Seoul: National Academy Press, 1992: 23-28.
[5] JIMÉNEZ J M, HULTMARK M, SMITS A J. The intermediate wake of a body of revolution at high Reynolds numbers[J]. Journal of Fluid Mechanics, 2010, 659: 516–539. doi: 10.1017/S0022112010002715
[6] JIMÉNEZ J M, REYNOLDS R T, SMITS A J. The effects of fin axials on the intermediate wake of a submarine model[J]. Journal of Fluids Engineering, 2010, 132(3): 031102. doi: 10.1115/1.4001010
[7] 张楠, 沈泓萃, 姚惠之. 潜艇喷流流场数值模拟研究[J]. 船舶力学, 2007, 11(1): 10–21. doi: 10.3969/j.issn.1007-7294.2007.01.002 ZHANG N, SHEN H C, YAO H Z. Numerical simulation of jet flow around submarine[J]. Journal of Ship Mechanics, 2007, 11(1): 10–21 (in Chinese). doi: 10.3969/j.issn.1007-7294.2007.01.002
[8] GUO H, GUO C Y, HU J, et al. Influence of jet flow on the hydrodynamic and noise performance of propeller[J]. Physics of Fluids, 2021, 33(6): 065123. doi: 10.1063/5.0051326
[9] 刘志华, 熊鹰, 王展志, 等. 潜艇新型整流方法的设计与试验研究[J]. 中国造船, 2010, 51(3): 47–55. doi: 10.3969/j.issn.1000-4882.2010.03.006 LIU Z H, XIONG Y, WANG Z Z, et al. Design and experimental study on a new wake control method of submarine[J]. Shipbuilding of China, 2010, 51(3): 47–55 (in Chinese). doi: 10.3969/j.issn.1000-4882.2010.03.006
[10] LIU Z H, XIONG Y, TU C X. Numerical simulation and control of horseshoe vortex around an appendage–body junction[J]. Journal of Fluids and Structures, 2011, 27(1): 23–42. doi: 10.1016/j.jfluidstructs.2010.08.006
[11] 赵鹏伟, 卢晓平, 孙玉明. 基于潜艇模型尾流湍流强度和耗散率的CFD模拟[J]. 中国舰船研究, 2014, 9(3): 43–48, 56. doi: 10.3969/j.issn.1673-3185.2014.03.006 ZHAO P W, LU X P, SUN Y M. CFD simulation of the wake turbulence intensity and the dissipation rating of a submarine model[J]. Chinese Journal of Ship Research, 2014, 9(3): 43–48, 56 (in Chinese). doi: 10.3969/j.issn.1673-3185.2014.03.006
[12] DIVSALAR K. Improving the hydrodynamic performance of the SUBOFF bare hull model: a CFD approach[J]. Acta Mechanica Sinica, 2020, 36(1): 44–56. doi: 10.1007/s10409-019-00913-7
[13] 田畅, 夏林生, 付敏飞, 等. 潜艇伴流场对螺旋桨激振力的影响[J]. 中国舰船研究, 2023, 18(3): 111–121. TIAN C, XIA L S, FU M F, et al. Influence of wake field on propeller exciting force of submarine[J]. Chinese Journal of Ship Research, 2023, 18(3): 111–121 (in Chinese).
[14] 田畅. 水下航行器伴流场对推进器激振力特性的影响研究[D]. 杭州: 浙江大学, 2022. TIAN C. Research on the influence of the wake field of underwater vehicles on propulsor exciting force characteristics[D]. Hangzhou: Zhejiang University, 2022 (in Chinese).
[15] RAHMANI M, JAFARI GAVZAN I, DEHGHAN MANSHADI M. Experimental investigation of the effect of sail geometry on the flow around the SUBOFF submarine model inspired by the dolphin's dorsal fin axial[J]. Ships and Offshore Structures, 2024, 19(6): 769–778. doi: 10.1080/17445302.2023.2208496
[16] 翟朔, 刘志华. 局部等厚度的共翼型舵对潜艇尾流场优化效果研究[J]. 推进技术, 2020, 41(7): 1660–1669. ZHAI S, LIU Z H. Research on optimization effect of modified conformal tail fin axial with a flat part on submarine wake field[J]. Journal of Propulsion Technology, 2020, 41(7): 1660–1669 (in Chinese).
[17] 姜宜辰, 李永坤, 王晴, 等. 附体位置对水下航行体伴流场影响规律研究[J]. 华中科技大学学报(自然科学版), 2021, 49(5): 32–37. JIANG Y C, LI Y K, WANG Q, et al. Research on influence of appendage position on wake field of underwater vehicle[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(5): 32–37 (in Chinese).
[18] BEIGI S M, SHATERI A, MANSHADI M D. Experimental study of the submarine's wake improvement by displacement of stern planes[J]. Ships and Offshore Structures, 2022, 17(9): 2103–2115. doi: 10.1080/17445302.2021.1979723
[19] 陈纪军, 潘子英, 彭超, 等. 十字形和X形艉舵航行体的水动力特性对比[J]. 中国舰船研究, 2020, 15(2): 8-16. CHEN J J, PAN Z Y, PENG C, et al. Comparison of hydrodynamic characteristics of SUBOFF with cruciform and X-form tail fin axial arrangement[J]. Chinese Journal of Ship Research, 2020, 15(2): 8-16 (in both Chinese and English).
[20] XIAO X, LIANG Q F, KE L, et al. Effects of X tail fin axial area on the horizontal mechanical properties and wake flow field of submarines[J]. Journal of Physics: Conference Series, 2021, 2095(1): 012089. doi: 10.1088/1742-6596/2095/1/012089
[21] 李孟捷, 王梦璇, 王力, 等. 水下航行体降噪艉翼填角的数值模拟与试验研究[J]. 船舶力学, 2016, 20(10): 1345–1354. doi: 10.3969/j.issn.1007-7294.2016.10.015 LI M J, WANG M X, WANG L, et al. Experiment and numerical simulation of denoising fillets of stern appendages on underwater vehicle[J]. Journal of Ship Mechanics, 2016, 20(10): 1345–1354 (in Chinese). doi: 10.3969/j.issn.1007-7294.2016.10.015
[22] TOXOPEUS S, KUIN R, KERKVLIET M, et al. Improvement of resistance and wake field of an underwater vehicle by optimising the fin axial-body junction flow with CFD[C]//Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco: ASME, 2014: V002T08A046.
[23] 梁秋凤, 叶金铭, 张露, 等. 潜艇舵翼分离型尾操纵面水动力及尾流场研究[J]. 舰船科学技术, 2021, 43(21): 33–38. LIANG Q F, YE J M, ZHANG L, et al. Research on hydrodynamic performance and wake flow field of submarine tail fin axial wing separated control surface[J]. Ship Science and Technology, 2021, 43(21): 33–38 (in Chinese).
[24] ITTC. ITTC–recommended procedures and guidelines[C]//Proceedings of the 25th International Towing Tank Conference. Fukuoka, Japan: ITTC, 2008.
[25] VAN DER PLOEG A. Object functions for optimizing a ship's aft body[C]//Proceedings of the 11th International Conference on Computer and IT Applications in the Maritime Industries (COMPIT), Liege, Belgium, 2012: 494-507.
[26] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge, MA: The MIT Press, 2006.
计量
- 文章访问数: 133
- HTML全文浏览量: 34
- PDF下载量: 30
