0.   引　言

船体梁崩溃是船舶营运过程中潜在的极为严重的事故，其后果往往包括巨额的财产损失、严重的环境污染，甚至是造成生命不可挽回的悲剧。目前，对船体梁进行总纵极限强度评估已成为确保船舶满足严格的安全标准不可或缺的措施之一。自Caldwell^[1]首次发表有关船体梁极限强度计算的论文以来，有关船体梁极限强度的研究工作得到了持续不断地展开，并积累了各种研究方法^[2-4]和丰富的研究成果^[5-6]。其中，由于计算机技术的迅猛发展和通用有限元软件的深度优化，采用非线性有限元分析方法研究船体梁的极限强度并获得高精度的结果已成为现实^[7-8]。然而，目前的研究多是基于单调递增载荷下的一次性静力极限强度评估理念，即认为船体梁的总体破坏是由于结构的危险截面在单一外部载荷作用下的一次性失效所引起。而事实上，船舶结构在实际营运过程中受到的外部载荷具有明显的循环属性。Liu和Soares^[9]计算发现，船体梁在循环弯矩下的极限强度往往低于单次弯矩下的极限强度；Xu等^[10]在研究中提到，作用于船体梁上的单次极端载荷可能并不会导致船体梁的整体崩溃，但由于局部构件发生屈曲产生的塑性行为，会导致船体梁的承载能力不断受到损伤。针对在单一外部载荷下评估船体梁极限强度时所存在的问题，部分学者认为基于循环载荷视角下考虑弹性安定特性的研究更能准确评估船体梁的极限强度。

安定效应主要用于研究在较大幅值范围的循环载荷下结构的弹塑性行为。Jones^[11]最早将安定理念引入船体梁的极限强度评估中，其研究表明，当考虑循环载荷下船体结构的弹性安定效应时，船体梁的纵向弯矩承载能力始终小于或不超过船体梁的一次性静力极限强度。Zhang等^[12]采用非线性有限元法计算了仅考虑焊接初始变形的某双壳油轮的临界弹性安定弯矩，发现临界弹性弯矩小于单调弯矩下的极限强度，这说明船体梁完全有可能在小于一次性静力极限强度的循环弯矩下发生崩溃。Li和Benson^[13]研究了初始变形对箱梁模型安定极限强度的影响。最近，笔者所在团队从组成船体梁的基本构件出发，在充分考虑结构的焊接初始变形与残余应力影响的基础上，研究了船体板^[14]、船体加筋板^[15]在循环载荷下的弹性安定特性，并结合非线性有限元法给出了面内循环载荷下基于弹性安定临界状态的船体加筋板极限强度预测公式^[16]。

以上关于循环弯矩下考虑弹性安定特性的船体结构极限强度研究工作非常有益于对船体结构极限强度的高精度评估，但所做工作依然不够充分，还有待进一步的探讨。针对目前研究中存在的不足，如考虑弹性安定特性的船体梁极限强度研究仍比较缺乏、通过非线性有限元法开展船体结构极限强度研究时普遍采用理想弹塑性材料模型而忽略了材料的塑性强化影响、常常忽略焊接残余应力的影响以及部分研究甚至完全不考虑焊接初始缺陷等，为了更准确地评估循环弯矩下船体梁的极限强度，获取其循环载荷的安全范围，拟对某双底散货船体梁开展循环弯矩下考虑弹性安定特性的极限强度数值模拟，并讨论不同材料模型、焊接初始变形与残余应力对循环弯矩下船体梁安定区间与极限强度的影响。

1.   非线性有限元模型

1.1   模型和材料参数

计算模型为某双底散货船体梁，具体的模型剖面形式参见文献[17]。通过非线性有限元软件ABAQUS进行建模分析，模型跨长取为5 220 mm。对散货船的船体梁进行单次加载计算时，选用理想弹性材料本构关系。当进行循环加载时，为了考虑结构在循环载荷作用下材料的包辛格效应，采用Chaboche模型^[18]，具体的材料参数如表1所示。表中，C₁～C₃和γ₁～γ₃为随动强化参数，$Q_{\infty}$为屈服面尺寸的最大变化，B为屈服面尺寸随塑性应变发展而变化的速率。计算时，取弹性模量E = 210 000 MPa，泊松比υ = 0.3，材料屈服强度${\sigma _{\text{Y}}}$= 315 MPa。

表  1  Chaboche模型材料参数^[18]

Table  1.  Material parameters of Chaboche model^[18]

参数	数值		参数	数值
E/MPa	210 000		C2/MPa	4 240
υ	0.3		γ2	52
σY/MPa	315		C3/MPa	1573
C1/MPa	13 921		γ3	14
γ1	765		Q∞/MPa	25.6

下载: 导出CSV 

| 显示表格

1.2   边界条件与加载

船体梁边界条件示意图如图1所示。边界条件采用船体梁非线性有限元数值模拟中经常使用的边界条件^[5]，即选取两端面的形心作为主节点A和主节点B，并将散货船船体梁两端面所有节点分别耦合到主节点（图中B节点的耦合未标出）。通过对两主节点施加绕x轴转动的强制转角，模拟船体梁受到的弯矩载荷。图中，U表示线位移，R表示转角位移，x指船体梁横向宽度方向，y指船体梁高度方向，z指船体梁纵向长度方向。

图  1  船体梁边界条件

Figure  1.  Boundary conditions of the bulk carrier

下载: 全尺寸图片 幻灯片

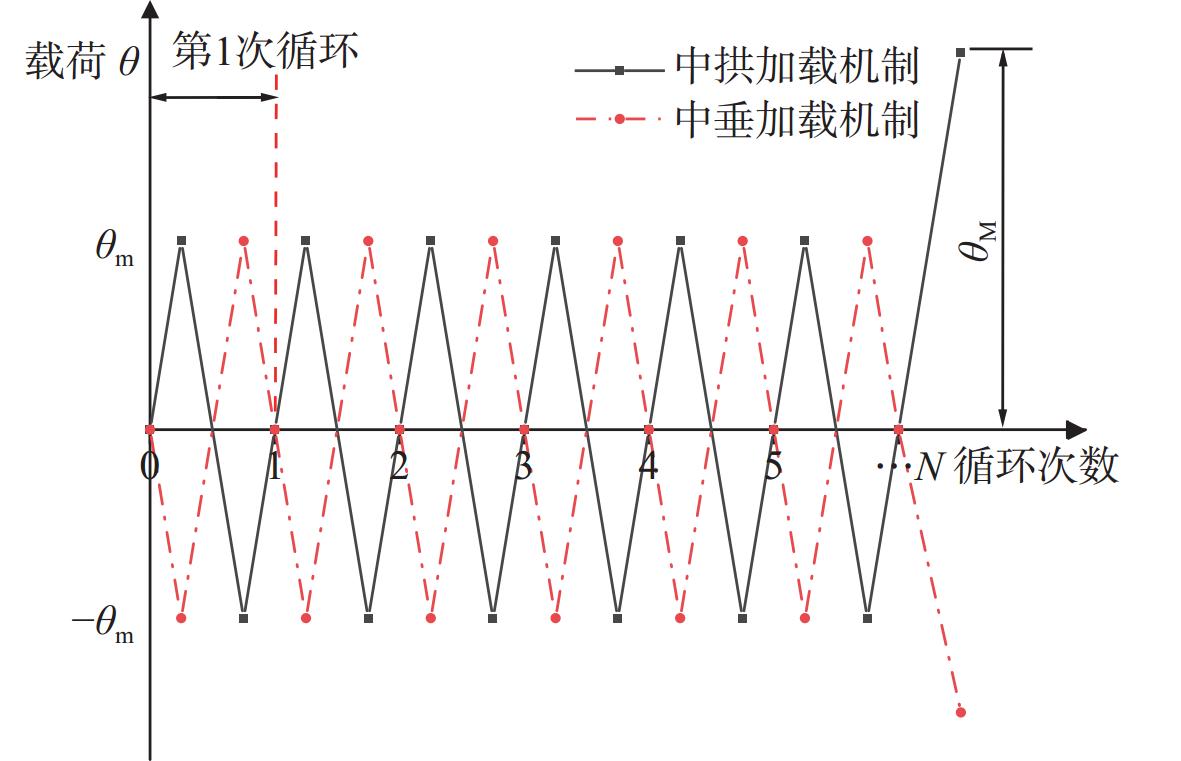
船舶在实际营运过程中，波浪载荷是最常见的外界载荷，由其引起的持续中拱和中垂弯矩对船舶剩余极限强度有着极其重要的影响。为了研究散货船船体梁在循环载荷下的弹性安定特性，示出了作用于散货船船体梁循环载荷的加载机制，如图2所示。首先，对散货船船体梁施加等幅循环弯矩载荷，船体梁产生了一定程度的塑性变形。随后，在最后一次循环时对其施加较大幅值的载荷，船体梁完全崩溃。图2中，${\theta _{\text{m}}}$为等幅循环载荷幅值，${\theta _{\text{M}}}$为最后一次较大载荷的幅值。

图  2  循环载荷示意图

Figure  2.  Schematic diagram of cyclic loading

下载: 全尺寸图片 幻灯片

1.3   焊接初始缺陷

船体梁的焊接初始缺陷主要包括焊接初始形变和残余应力。为了更准确地评估散货船的极限强度，对焊接初始形变和残余应力进行了综合考虑。

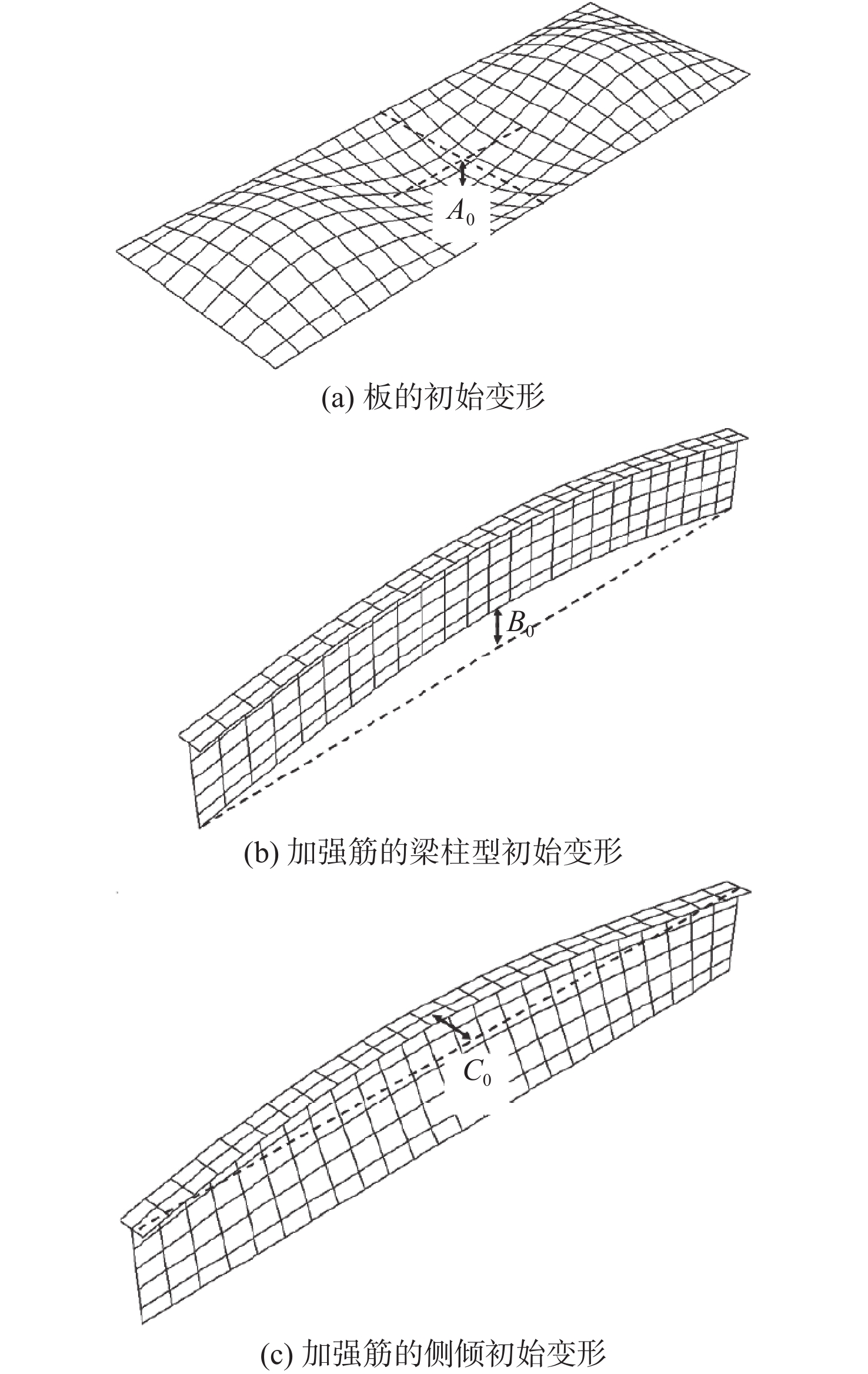
本文从板、加强筋的梁柱型以及加强筋侧倾的初始变形这3个方面考虑了船体加筋板的初始变形^[19]，变形示意图如图3所示。

图  3  焊接初始变形示意图

Figure  3.  Schematic diagram of welding initial deformation

下载: 全尺寸图片 幻灯片

板的整体初始变形：

加强筋的梁柱型初始变形：

加强筋的侧倾初始变形：

式中：$A_{0}$，$B_{0}$和$C_{0}$分别为3种初始变形的幅值；$a$为模型跨长；$b$为相邻纵骨间距；$B$为加筋板总宽；h为加强筋高度；m为板的纵向屈曲半波数，其值为满足不等式$a / b \leq \sqrt{m(m+1)}$的最小整数。对初始变形幅值取平均级别：$A_{0}=0.1 \beta^{2} t_{\mathrm{p}}$，B₀ = C₀ = 0.001 5a，其中$\beta$为柔度系数，$\beta=\left(b / t_{\mathrm{p}}\right) \sqrt{\sigma_{\mathrm{Y}} / E}$，$t_{\mathrm{p}}$为板厚。

目前，已有多种关于加筋板焊接残余应力的分布形式，本文选取较为简化的矩形分布形式，同时，对焊接残余拉压应力采用平均级别。详细的焊接残余应力区以及焊接残余拉压应力计算公式参见文献[20]。含有焊接初始变形与残余应力的散货船船体梁有限元模型如图4所示。

图  4  含有焊接初始缺陷的船体梁有限元模型

Figure  4.  Finite element model for the hull girder with welding initial imperfections

下载: 全尺寸图片 幻灯片

1.4   网格策略与有限元方法验证

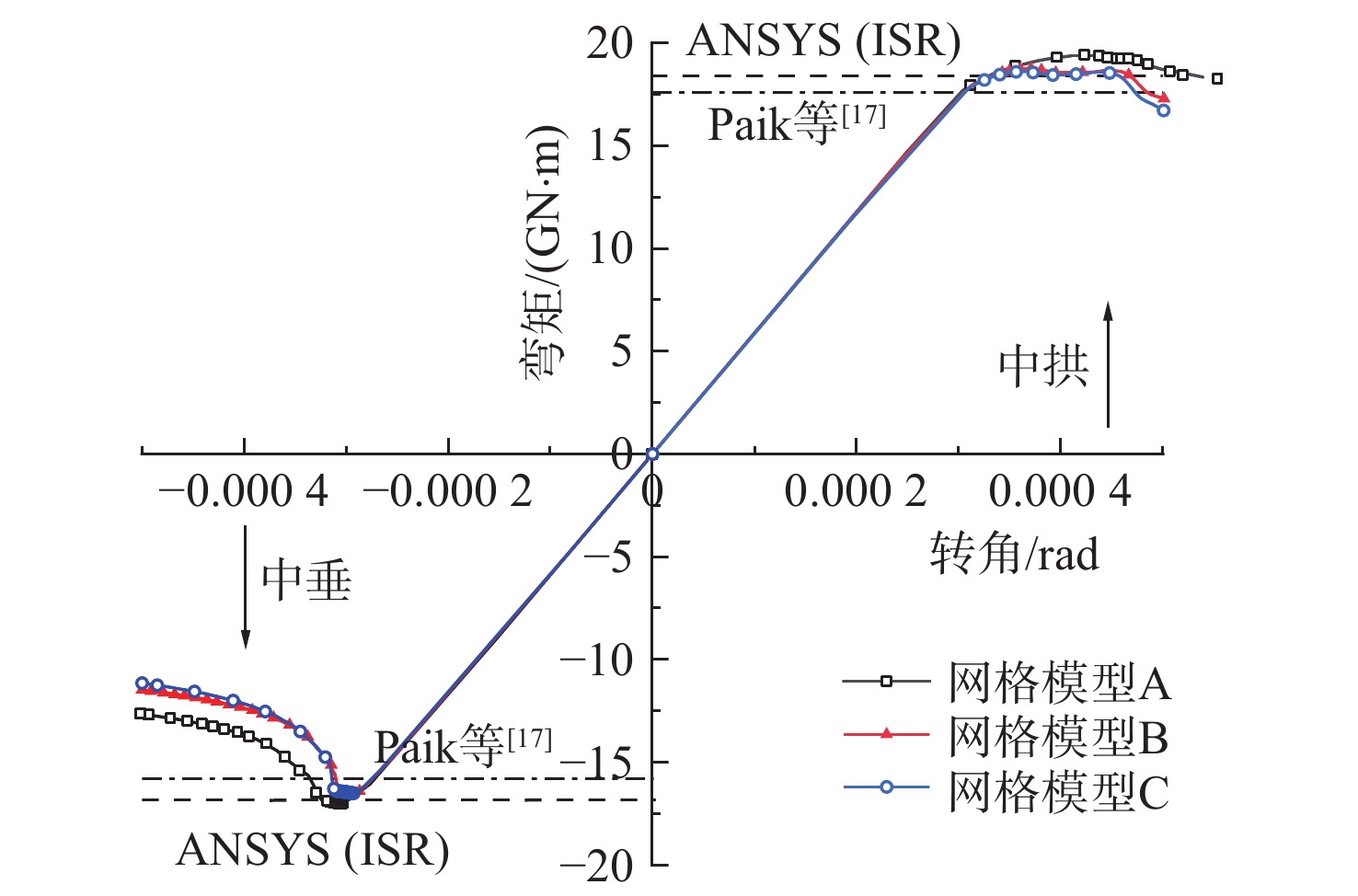
本文选用3种不同的网格模型对散货船船体梁进行网格收敛性分析，具体的网格划分策略如表2所示。通过与印度船级社（Indian register of shipping，ISR）的已有结果的对比，验证了本文计算结果的准确性（图5）。在中拱弯矩下，通过网格模型B得到的船体梁极限强度相比网格模型A提升了3.41%，而由网格模型C得到的极限强度相比网格模型B只提升了0.74%。在中垂弯矩下也得到了类似的结果。由于网格模型C在计算中会消耗大量的时间，而其对计算结果精度的提升效果并不明显，故本文选用网格模型B开展后续的计算。

表  2  网格收敛性分析

Table  2.  Grid convergence analysis

网格模型	网格数量			散货船船体梁模型单元总数	弯矩(本文计算值)/(GN∙m)			提升效果/%
	相邻加强筋之间	加强筋腹板	板纵长方向		中拱	中垂		中拱	中垂
A	7	3	35	97 020	19.402	17.015
B	9	5	49	182 182	18.741	16.578		3.41	2.57
C	11	6	63	285 768	18.603	16.504		0.74	0.45

下载: 导出CSV 

| 显示表格

图  5  不同网格策略下的船体梁弯矩-转角曲线

Figure  5.  Bending moment-rotation curves of hull girder under different grid strategies

下载: 全尺寸图片 幻灯片

1.5   循环载荷下船体结构响应

图6所示为船体梁在不同载荷幅值下的结构响应示意图。由图可见，在完全弹性阶段，作用于船体梁结构的循环载荷幅值较小，故结构中尚未出现塑性变形；随着循环载荷幅值的增大，结构会在循环载荷下产生塑性变形；经历一定次数的循环后，船体结构的整体塑性变形不再增加，船体梁会达到弹性安定状态；随着循环载荷幅值的进一步增加，结构会在循环载荷作用下发生塑性累积破坏。图中：θ₁，θ₂分别为弹性安定下限与上限对应的转角；M₁，M₂分别为达到弹性安定下限与上限时对应的弯矩值；${\theta _{\text{U}}}$为船体梁极限强度对应的转角；${M_{\text{U}}}$为船体梁极限强度。

图  6  不同载荷幅值下的船体梁结构响应示意图

Figure  6.  Response of the hull girder structural under different load amplitudes

下载: 全尺寸图片 幻灯片

2.   计算结果

2.1   散货船船体梁弹性安定上、下限

本文对散货船船体梁施加了8次双向等幅循环载荷，并在最后一次循环卸载后进行了反向加载用以获取其剩余极限强度。双底散货船体梁为上下非对称结构，当其处于中拱与中垂状态时，受载情况不同。当船体梁第1次加载，所受载荷为中拱弯矩时，认为经过图2所示的循环加载后求出的是双底散货船体梁中拱状态下的弹性安定特性；当船体梁第1次加载，所受载荷为中垂弯矩时，认为经过图2所示的循环加载后求出的是双底散货船体梁在中垂状态下的弹性安定特性。可通过改变循环载荷幅值${\theta _{\text{m}}}$的大小，获取船体梁在每个循环卸载后的船体梁端面剩余转角变化，来确定散货船船体梁的弹性安定上限。近似界定散货船船体梁达到弹性安定状态如下：本文散货船船体梁经历预设的8次等幅循环弯矩后，因塑性变形的产生，各次循环卸载后船体梁端面将出现剩余转角；当第8次循环卸载后，船体梁端面的剩余转角较之前的循环未显著增加而是趋于稳定。不考虑焊接初始缺陷、仅考虑焊接初始变形，以及考虑焊接初始变形与残余应力的散货船船体梁在每次循环卸载后的剩余转角变化如图7所示。

图  7  散货船船体梁卸载后的剩余转角变化

Figure  7.  Variation of residual rotation angle of bulk carrier's hull girder after unloading

下载: 全尺寸图片 幻灯片

图7（a）显示，当施加的载荷幅值低于2.90×10⁻⁴ rad时，散货船船体梁在各个循环下卸载后的剩余转角保持不变；当施加的载荷幅值高于2.90×10⁻⁴ rad时，散货船船体梁的剩余转角突破了弹性安定上限；由于塑性不断累积，在超过弹性安定上限幅值2.90×10⁻⁴ rad的循环弯矩作用下，散货船船体梁的剩余转角逐步增加。图7（c）和图7（d）与图7（a）同理。图7（b）显示，散货船船体梁在一个完整循环周期内是先经历中垂弯矩，然后经历中拱弯矩；在载荷幅值较低（低于2.90×10⁻⁴ rad）的水平下，散货船船体梁在各个循环下卸载后的剩余转角保持不变，达到弹性安定；当载荷幅值较高（2.95×10⁻⁴，3.0×10⁻⁴ rad）时，散货船船体梁在第1次循环卸载后将遗留部分中拱弯矩卸载后的转角，即剩余转角为负值；从第2次循环载荷卸载开始，由于在后续加载过程中塑性累积不断增加，剩余转角会因中垂弯矩的作用使得后续循环卸载后的剩余转角不断增加且变化为正值。由于焊接残余应力的存在会降低散货船船体梁的抗弯刚度，在材料延性足够的前提下，如图7（e）和图7（f）所示，施加的载荷幅值越大，散货船船体梁卸载后的剩余转角可能越小。

通过观察散货船船体梁在第1个加载循环周期内最先出现的塑性变形时刻云图，确定散货船船体梁的弹性安定下限。以只考虑焊接初始变形模型为例，散货船船体梁在不同加载机制下最先出现塑性应变时的塑性分布如图8所示，该时刻所对应的加载转角即为散货船船体梁的弹性安定下限。考虑不同焊接初始缺陷的散货船船体梁的弹性安定上、下限如表3所示，从中可以发现，焊接初始缺陷的存在明显影响散货船船体梁的弹性安定下限，焊接初始缺陷考虑越完整，散货船船体梁的弹性安定下限越低。

图  8  散货船船体梁首次出现塑性应变时的塑性分布（只考虑焊接初始变形）

Figure  8.  The plastic distribution of bulk carrier's hull girder when plastic strain appears for the first time (only consider the initial welding deformation)

下载: 全尺寸图片 幻灯片

表  3  散货船船体梁弹性安定上、下限的载荷幅值

Table  3.  Load amplitudes of the upper and lower limits for the elastic shakedown of bulk carrier's hull girder

散货船船体梁	受载状态	载荷幅值/rad
		安定下限	安定上限
不考虑焊接初始缺陷	中拱	2.005×10−4	2.90×10−4
	中垂	1.982×10−4	2.90×10−4
仅考虑焊接初始变形	中拱	1.573×10−4	2.80×10−4
	中垂	1.652×10−4	2.85×10−4
考虑焊接初始变形与残余应力	中拱	0.702×10−4	2.70×10−4
	中垂	0.773×10−4	2.85×10−4

下载: 导出CSV 

| 显示表格

2.2   散货船船体梁弹性安定区间

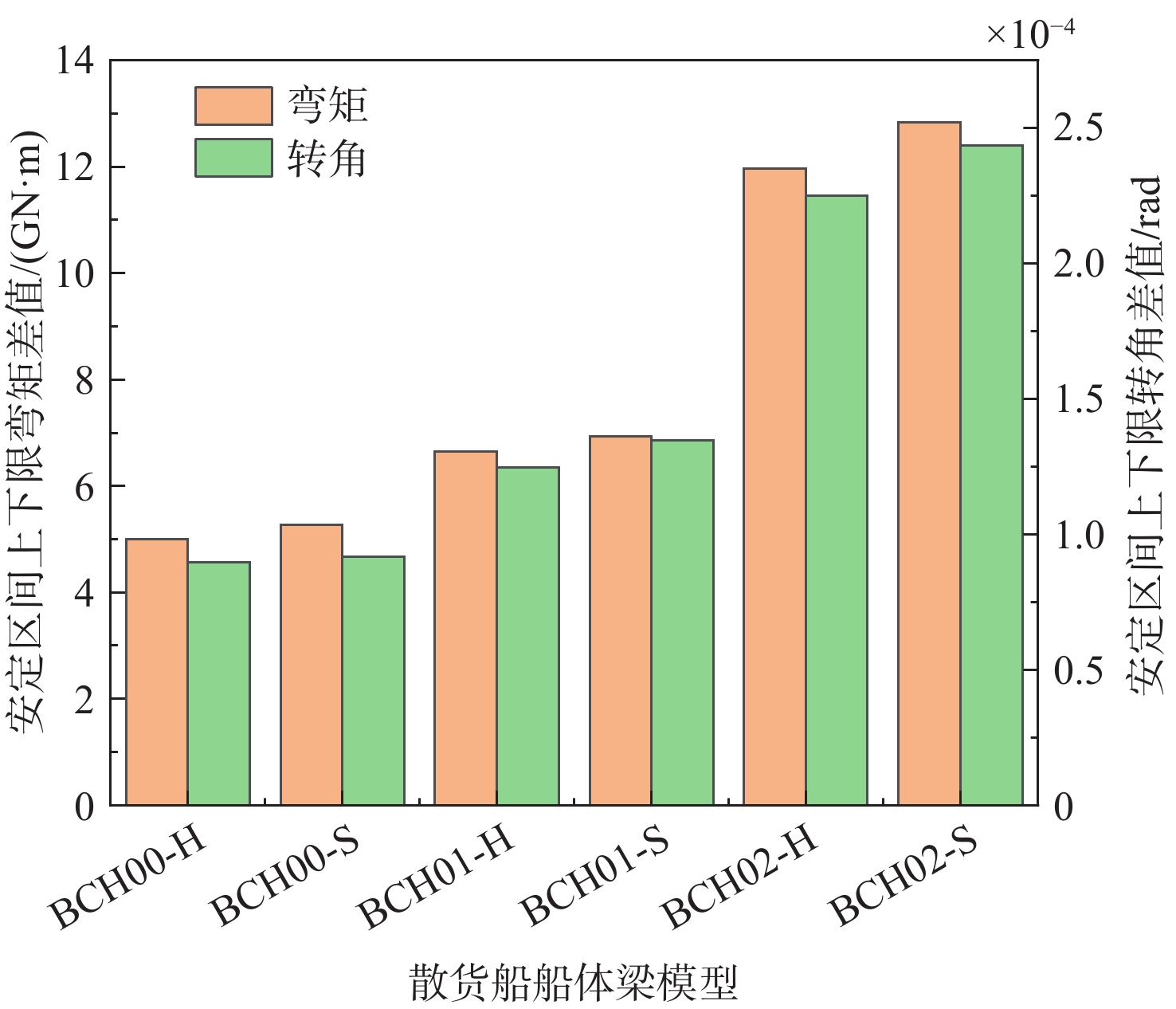
考虑不同焊接初始缺陷的散货船船体梁弹性安定区间分布如图9所示，其中M_H和M_S分别为船体梁中拱、中垂时的弯矩。散货船船体梁不同状态时刻的极限强度值如表4所示。散货船船体梁的弹性安定区间长度如图10所示，其中BCH表示散货船船体梁；00，01和02分别表示不考虑焊接初始缺陷、只考虑初始变形、考虑初始变形与残余应力的散货船船体梁模型；H表示中拱；S表示中垂。由图10可以发现，对焊接初始缺陷考虑得越全面，散货船船体梁在中拱及中垂状态下的弹性安定区间范围越大。结合表4，说明考虑焊接初始变形与残余应力的散货船船体梁模型在经受较小的循环载荷时，结构会更早地发生塑性变形。

图  9  散货船船体梁弹性安定区间分布

Figure  9.  Distribution of the elastic shakedown interval of bulk carrier's hull girder

下载: 全尺寸图片 幻灯片

表  4  散货船船体梁弹性安定上、下限的极限强度

Table  4.  The ultimate strength of upper and lower limits of elastic shakedown of bulk carrier's hull girder

散货船船体梁	受载状态	极限强度/(GN∙m)
		M1	M2	MU
不考虑焊接初始缺陷	中拱	11.781	16.789	19.340
	中垂	11.568	16.836	17.074
仅考虑焊接初始变形	中拱	8.726	15.259	18.952
	中垂	9.246	15.359	15.938
考虑初始变形与残余应力	中拱	3.837	14.428	18.747
	中垂	4.374	15.194	14.864

下载: 导出CSV 

| 显示表格

图  10  散货船船体梁安定区间长度

Figure  10.  Elastic shakedown length of bulk carrier's hull girder

下载: 全尺寸图片 幻灯片

2.3   弹性安定状态下散货船船体梁极限强度

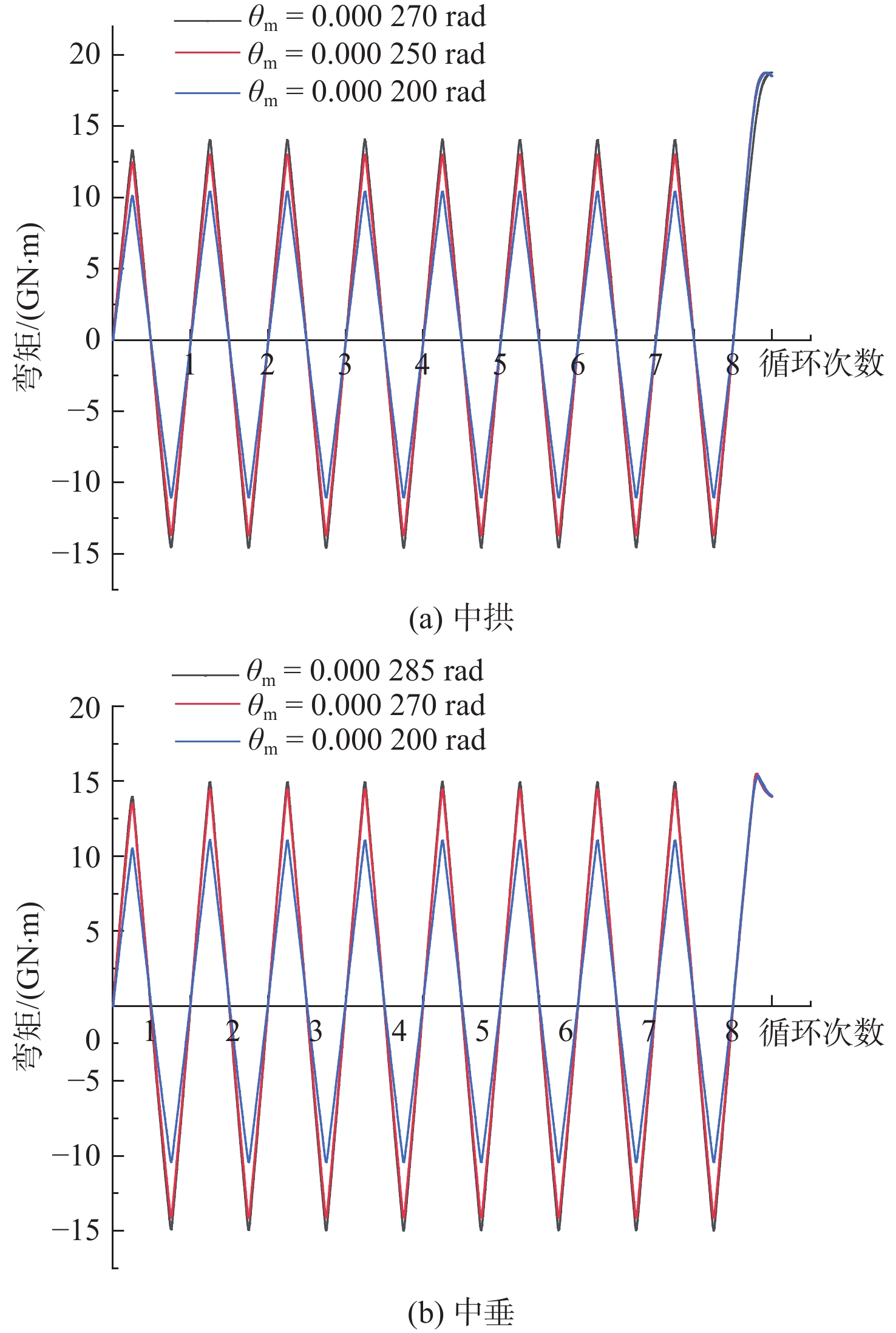
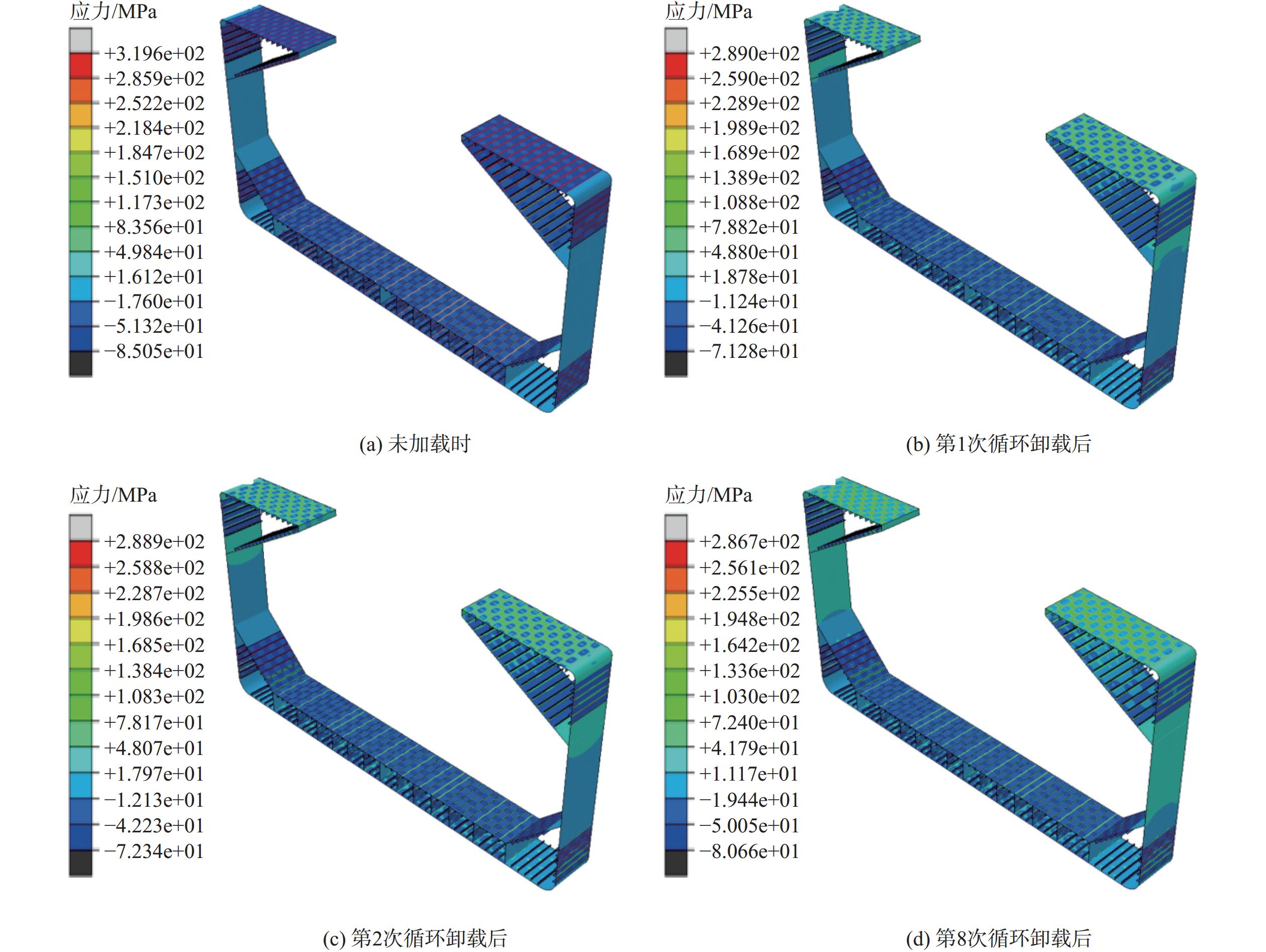
考虑焊接初始变形与残余应力的散货船船体梁在不同循环载荷幅值下的弯矩变化如图11所示，其在未加载以及第1，2，8次循环卸载后的轴向应力云图如图12所示。从中可以发现，散货船船体梁在第1次达到中拱或中垂时的弯矩值均低于后续循环过程中达到中拱或中垂时的弯矩值。这说明经过第1次循环后焊接残余应力得到了较大程度的释放，使得在后续循环过程散货船船体梁的中拱或中垂弯矩值得到了提高。同时，随着循环载荷幅值的增大，散货船船体梁在第1次达到中拱或中垂时的弯矩值与后续循环过程中的弯矩值相差越大，这说明在弹性安定区间内，循环载荷幅值越大，散货船船体梁的焊接残余应力越能够得到释放。

图  11  散货船船体梁循环过程中弯矩的变化

Figure  11.  Variation of the bending moment of bulk carrier's hull girder during cyclic process

下载: 全尺寸图片 幻灯片

图  12  散货船船体梁轴向应力云图

Figure  12.  Axial von Mises stress contours of bulk carrier's hull girder

下载: 全尺寸图片 幻灯片

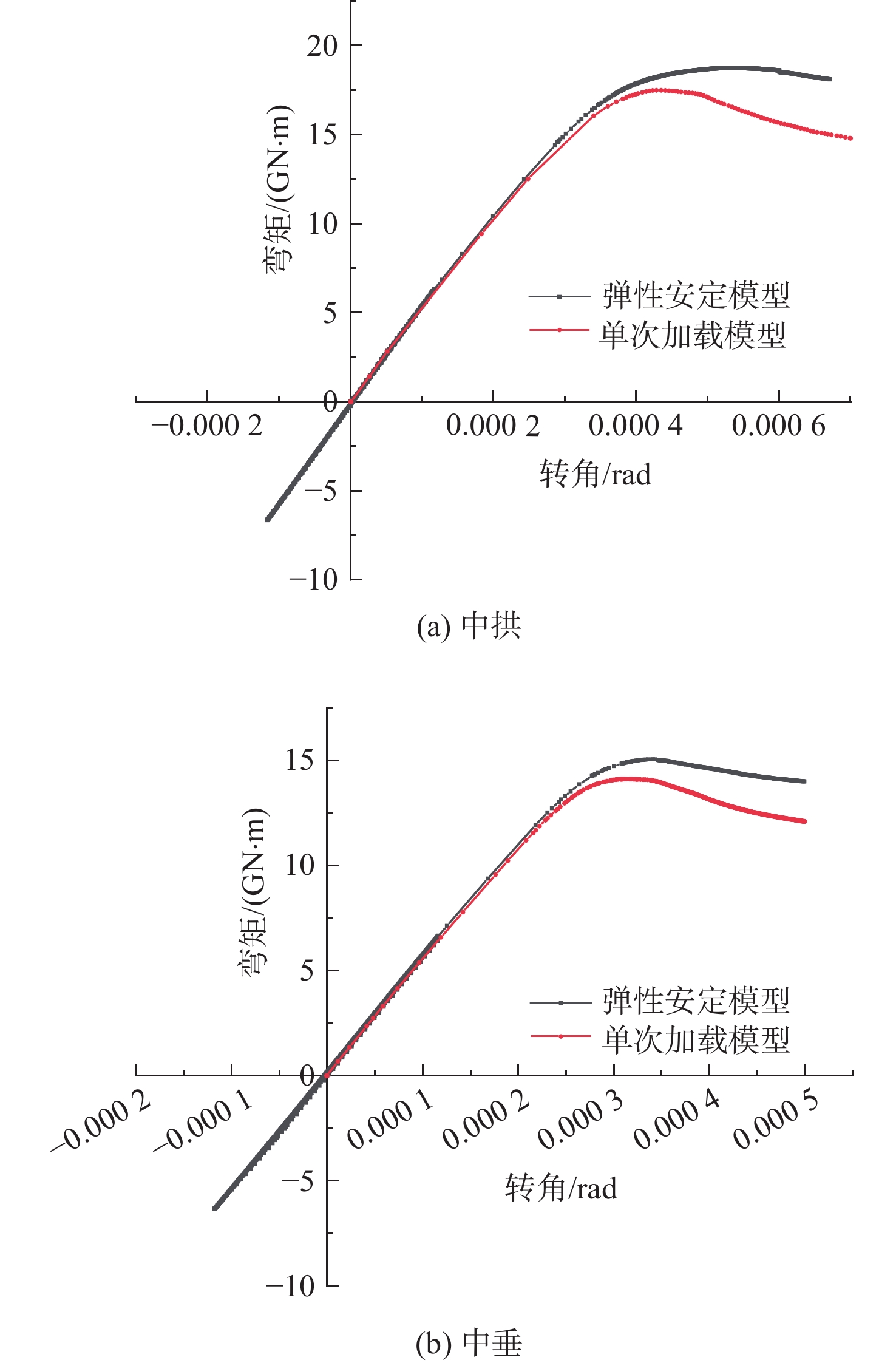
在弹性安定区间内取值，取${\theta _{\text{m}}}$= 0.000 12 rad时循环8次计算得到的处于弹性安定状态下考虑完整焊接初始缺陷的散货船船体梁的弯矩-转角曲线与单次加载时的弯矩-转角曲线的对比如图13所示。由图可发现，在循环加载过程中，由于焊接残余应力释放与塑性累积的耦合影响，处于弹性安定状态下的散货船船体梁的极限强度高于单次加载时的，其在中拱、中垂状态下分别提升了7.15%和5.68%。

图  13  弯矩-转角曲线

Figure  13.  Bending moment-rotation curves

下载: 全尺寸图片 幻灯片

3.   结　论

本文在循环弯矩下对某散货船船体梁进行了弹性安定特性研究，并在研究中考虑了结构在反向加载时材料的包辛格效应、焊接初始变形与残余应力的影响，主要得到如下结论：

1）焊接初始缺陷对散货船船体梁弹性安定区间有明显影响。焊接初始变形与残余应力均会使散货船船体梁的弹性安定上、下限降低，当完整考虑焊接初始变形与残余应力时，散货船船体梁的弹性安定下限下降最明显，其弹性安定区间范围最大。

2）在散货船船体梁的循环加载过程中，焊接残余应力主要在一次循环中得到释放，在达到弹性安定状态后趋于稳定，且循环载荷幅值越大，散货船船体梁的焊接残余应力越能得到释放。

3）对于考虑焊接初始变形与残余应力的散货船船体梁，在循环加载过程中，在焊接残余应力释放与塑性累积的耦合影响下，处于弹性安定状态下的散货船船体梁的极限强度高于单次加载时的极限强度，其在中拱、中垂状态下分别提升了7.15%和5.68%。