Data-driven unmanned surface vehicles trajectory tracking adaptive control
-
摘要:目的
针对具有参数不确定性的无人船系统,提出一种基于数据驱动的无人船轨迹跟踪控制策略。
方法首先,运用反步法设计无人船运动学子系统的虚拟控制信号,确保系统轨迹跟踪的准确性;其次,通过数据驱动的方法设计无人船动力学子系统的控制器,减轻未知扰动等不确定性因素带来的影响,降低控制器设计的复杂程度。
结果采用递归原理,通过分析系统伪雅可比矩阵、动力学和运动学跟踪误差收敛,证明了系统的稳定性。
结论仿真结果表明,所提控制策略可以对无人船期望轨迹进行有效跟踪,验证了控制方案的有效性。
Abstract:ObjectivesA data-driven trajectory tracking control scheme is proposed for unmanned surface vehicles (USVs) with uncertain parameters.
MethodsFirst, the USV kinematics subsystem is processed by the backstepping, and we can obtain the virtual control signal of the kinematics subsystem which ensure the accuracy of the system trajectory tracking. Secondly, the data-driven is used to deal with the USV dynamics subsystem to get the controller which reduces the impact of uncertainties such as unknown disturbances and reduce the complexity of controller design.
ResultsThe stability of the system is proved by analyzing the pseudo Jacobian matrix and the convergence of the tracking error of dynamics and kinematics.
ConclusionsSimulation results show that the control strategy proposed in this paper can track the expected trajectory effectively, and the effectiveness of the control scheme is verified.
-
Keywords:
- unmanned vehicles /
- trajectory tracking /
- backstepping control /
- data-driven /
- motion control
-
0. 引 言
无人船(unmanned surface vehicle, USV)是一种水面航行机器人。随着我国“海洋强国”战略的推进,无人船控制技术的重要性日益凸显,并在海洋运输、资源探测、安防救援、水域清洁等领域得到广泛应用。
无人船的轨迹跟踪控制是实现其附加功能的基础。轨迹跟踪控制是指在控制系统作用下,无人船从初始位置驶入预规划航线,并沿期望轨迹抵达目的地,同时保持稳定。近年来,无人船轨迹跟踪系统研究不断深入,学者们提出了许多理论方法,例如比例−积分−微分(PID)控制、反步法、神经网络控制、模型预测控制等[1-2]。反步法作为一种非线性系统控制器设计框架,因便捷、有效而被广泛采用。例如,关海滨等[3]基于反步法提出了一种稳定性及实用性较好的跟踪方法。张凯等[4]、Yang等[5]针对无人船系统存在的不确定扰动问题,引入扰动观测器,通过估计未知扰动前馈补偿,提高系统跟踪性能。张昕[6]、邢道奇等[7]、Chen等[8]依据滑模控制对系统不确定扰动的鲁棒性,在反步法基础上引入动态滑模技术,增强系统抗干扰能力。冯鑫等[9]将积分滑膜控制与模型预测控制相结合,提出基于滑膜预测控制的轨迹跟踪控制器。在确保系统鲁棒性的同时,提高控制系统跟踪性能。然而,由于实际被控系统存在模型参数不确定性等问题,上述方法所设计的控制器难以保证高跟踪精度。
当被控系统准确模型难以建立时,数据驱动控制成为合适选择。数据驱动控制[10]是指控制器设计不显含受控过程的数学模型信息,仅利用受控系统在线或离线I/O数据及数据处理得到的知识设计控制器。利用数据驱动方法处理无人船系统中模型参数不确定的非线性方程,可使控制系统摆脱对复杂时变数学模型的依赖,优化设计过程。
目前,数据驱动方法在无人船轨迹跟踪系统中应用广泛。廖煜雷等[11]针对无人船存在模型不确定、外部干扰问题,提出一种无模型自适应艏向控制方法。李诗杰等[12]将数据驱动方法应用于无人船自抗扰控制器设计,依据数据驱动方法建立的实际舵角与期望航向角间的非线性关系,设计自抗扰无模型控制器,有效跟踪系统实时状态,实现稳定航迹控制。
Weng等[13]提出一种数据驱动鲁棒跟踪控制方案,通过设计新的数据驱动滑模曲面,保证系统强鲁棒性,提高系统的跟踪性能。Wang等[14]提出基于数据驱动的强化学习控制方案,在提高系统跟踪精度的同时追求控制最优性。因此,数据驱动方法在无人船轨迹跟踪系统中的应用,可有效降低系统未知参数及不确定扰动对跟踪效果的影响,实现对期望轨迹的有效跟踪。但是实际系统模型中部分参数已知且可利用,单纯使用数据驱动方法无法有效利用模型已知条件,不利于无人船系统稳定跟踪。
综上所述,本文拟针对无人船轨迹跟踪问题,提出一种反步法与数据驱动控制(基于紧格式动态线性化(CFDL))相结合的轨迹跟踪控制策略。同时,进行基于数据驱动无人船轨迹跟踪控制的仿真分析,验证所提控制算法的有效性。
1. 无人船数学模型
无人船的运动学和动力学模型可通过下列状态方程描述:
\left\{ \begin{gathered} {\boldsymbol{\dot \eta }} = {\boldsymbol{R}}(\varphi ){\boldsymbol{\nu }} \\ {\boldsymbol{M\dot \nu }} = {\boldsymbol{\tau }} - {\boldsymbol{C}}({\boldsymbol{\nu }}){\boldsymbol{\nu }} - {\boldsymbol{D}}({\boldsymbol{\nu }}){\boldsymbol{\nu }} + {\boldsymbol{d}} \\ \end{gathered} \right. (1) 式中: {\boldsymbol{\eta }} = {\left[ {x,y,\varphi } \right]^{\rm{T}}} ,为实际运行轨迹,其中x和y为无人船位置坐标,\varphi 为航向角; {\boldsymbol{\nu}} = {\left[ {u,v ,r } \right]^{\rm{T}}} ,为无人船速度向量; {\boldsymbol{d}} = {[{d _x}, {d _ y}, {d _{\varphi} }]^{\rm{T}}} ,为外界未知的扰动因素; {\boldsymbol{\tau }} = {[{\tau _1},{\tau _2},{\tau _3}]^{\rm{T}}} ,为系统的控制器输入; {\boldsymbol{M}} \in {{\bf{R}}^{3 \times 3}} ,为无人船质量以及船体附加质量组成的惯性矩阵; {\boldsymbol{R}}(\varphi ) \in {{\bf{R}}^{3 \times 3}} ,为无人船体坐标系与大地坐标系之间的坐标变换矩阵,满足 {{\boldsymbol{R}}^{ - 1}}(\varphi ) = {{\boldsymbol{R}}^{\rm{T}}}(\varphi ) ; {\boldsymbol{C}}({\boldsymbol{v}}) \in {{\bf{R}}^{3 \times 3}} ,为科里奥利向心力矩阵; {\boldsymbol{D}}({\boldsymbol{v}}) \in {{\bf{R}}^{3 \times 3}} ,为水面阻尼矩阵。其中,
\begin{split} & \quad\; \boldsymbol{M}=\left[\begin{matrix}m_{11} & 0 & 0 \\ 0 & m_{22} & 0 \\ 0 & 0 & m_{33}\end{matrix}\right] \\ & \boldsymbol{R}(\varphi)=\left[\begin{matrix}\cos(\varphi) & -\sin(\varphi) & 0 \\ \sin(\varphi) & \cos(\varphi) & 0 \\ 0 & 0 & 1\end{matrix}\right]\end{split} {\boldsymbol{C}}({\boldsymbol{\nu }}) = \left[ \begin{matrix} 0&0&{{c_{13}}} \\ 0&0&{{c_{23}}} \\ { - {c_{13}}}&{ - {c_{23}}}&0 \end{matrix} \right] ,\quad {\boldsymbol{D}}({\boldsymbol{\nu }}) = \left[ \begin{matrix} {{d _{11}}}&0&0 \\ 0&{{d _{22}}}&0 \\ 0&0&{{d _{33}}} \end{matrix} \right] 式中: {m_{11}} , {m_{22}} 和 {m_{33}} 为水面无人船系统自身质量及各种附加质量在内的惯性参数; {d _{11}} , {d _{22}} 和 {d _{33}} 为水动力阻尼系数; {c_{13}} = - {m_{22}}v ; {c_{23}} = {m_{11}}u 。
2. 无人船轨迹跟踪控制器设计
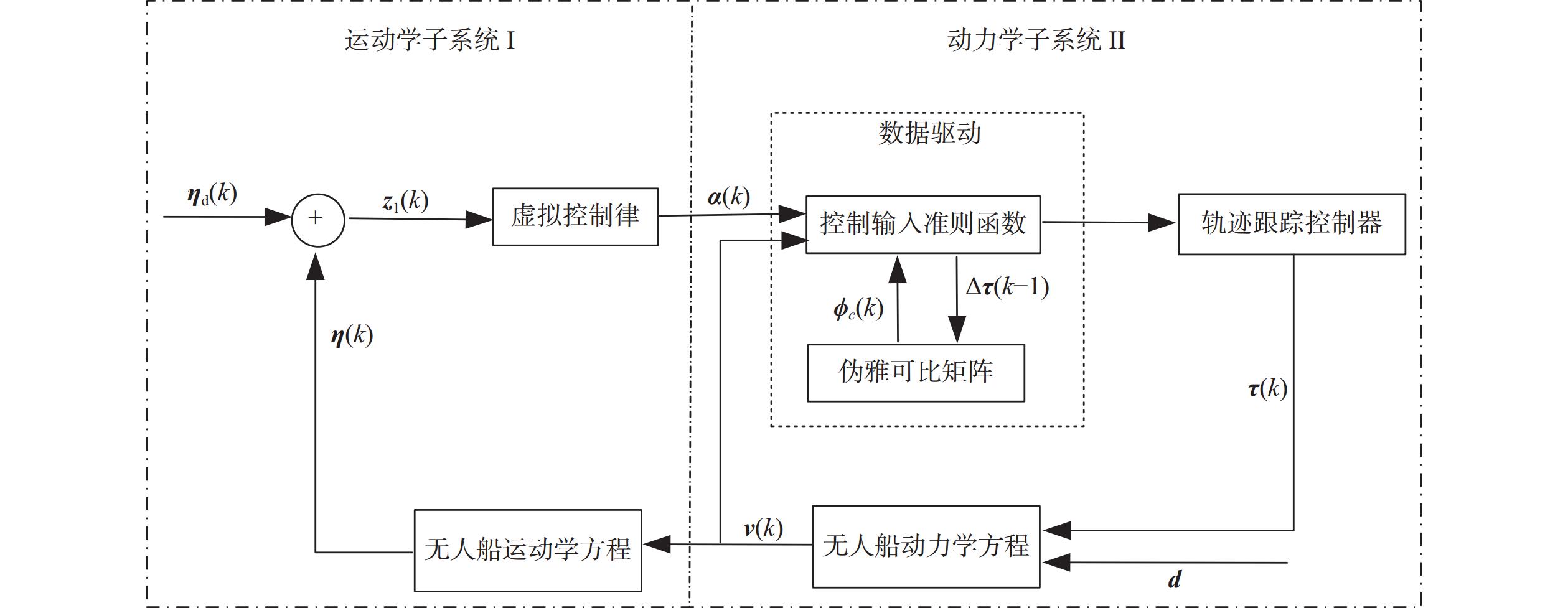
控制器设计的主要思路为:针对运动学子系统I中的 {\boldsymbol{\dot \eta }} = {\boldsymbol{R}}(\varphi ){\boldsymbol{\nu }} ,应用反步设计方法获取虚拟控制量 {\boldsymbol{\alpha}} (k) ,并将 {\boldsymbol{\alpha}} (k) 作为动力学子系统II中的期望输出,进而实现对控制器输入 {\boldsymbol{\tau}} (k) 的求解。
基于数据驱动的无人船轨迹跟踪控制器设计原理框图如图1所示。其中,{{\boldsymbol{\eta }}_{\rm{d}}(k)} 为期望运行轨迹;z1(k)为运动学模型跟踪误差;{{\boldsymbol{\phi }}_{{c}} }({k}) 为伪雅可比矩阵(pseudo Jacobian matrix, PJM);∆τ(k−1)为上一时刻的输入增量。
2.1 模型离散化
假设采样时间为 T ,对式(1)进行离散化,可得
\left\{ \begin{aligned} & {{{\boldsymbol{x}}_1}({k} + 1) = {{\boldsymbol{x}}_1}({k}) + T{\boldsymbol{R}}({\varphi _{k}}){{\boldsymbol{x}}_2}({k}){\text{ }}} \\ & {{\boldsymbol{x}}_2}({k} + 1) = ({\boldsymbol{I}} - T{{\boldsymbol{M}}_{{n}}}){{\boldsymbol{x}}_2}({k}) + T{{\boldsymbol{C}}_n}({{\boldsymbol{v}}_{{k}}}) + T{{\boldsymbol{d}}_{{n}}} + T{\boldsymbol{N\tau }}({k}) \end{aligned}\right. (2) 式中:I为单位矩阵; {{\boldsymbol{x}}_1}({k}) = {\boldsymbol{\eta }}({k}) , {{\boldsymbol{x}}_2}({k}) = {\boldsymbol{v}}({k}) ,
\boldsymbol{M}_n=\left[\begin{matrix}\dfrac{d_{11}}{m_{11}} & 0 & 0 \\0 & \dfrac{d_{22}}{m_{22}} & 0 \\0 & 0 & \dfrac{d_{33}}{m_{33}}\end{matrix}\right] \boldsymbol{C}_n(\boldsymbol{\nu}_k)\text{ = }\left[\begin{matrix}\dfrac{m_{22}}{m_{11}}v(k)r(k) \\-\dfrac{m_{11}}{m_{22}}u(k)r(k) \\\dfrac{m_{11}-m_{22}}{m_{33}}u(k)v(k)\end{matrix}\right] {{\boldsymbol{d}}_{{n}}} = \left[ \begin{matrix} {\dfrac{{{d _{{x}}}}}{{{m_{11}}}}} \\ {\dfrac{{{d _{{y}}}}}{{{m_{22}}}}} \\ {\dfrac{{{d _{\varphi} }}}{{{m_{33}}}}} \end{matrix} \right] ,\;\;\; {\boldsymbol{N}} = \left[ \begin{matrix} {\dfrac{1}{{{m_{11}}}}}&0&0 \\ 0&{\dfrac{1}{{{m_{22}}}}}&0 \\ 0&0&{\dfrac{1}{{{m_{33}}}}} \end{matrix}\right] 2.2 控制器设计
2.2.1 运动学模型控制系统I
定义参考向量 {{\boldsymbol{x}}_{\rm{d}}} ,则运动学模型跟踪误差 {{\boldsymbol{z}}_1} 表示为
{{\boldsymbol{z}}_1}({k}) = {{\boldsymbol{x}}_1}({k}) - {{\boldsymbol{x}}_{\rm{d}} }({k}) (3) 可得
\begin{split} & {{\boldsymbol{z}}_1}({k} + 1) = {{\boldsymbol{x}}_1}({k} + 1) - {{\boldsymbol{x}}_{\rm{d}}}({k} + 1) =\\&\;\;\; {{\boldsymbol{x}}_1}({k}) + T{\boldsymbol{R}}({\varphi _{k}}){{\boldsymbol{x}}_2}({k}) - {{\boldsymbol{x}}_{\rm{d}}}({k} + 1) \end{split} (4) 取Lyapunov函数
{{\boldsymbol{V}}_1}({k}) = \frac{1}{2}{{\boldsymbol{z}}_1}^{\rm{T}}({k}){{\boldsymbol{z}}_1}({k}) (5) 可得
\begin{split} & \qquad\Delta {V}_{1}=\frac{1}{2}{\boldsymbol{z}}_{1}^{\rm{T}}( k+1){\boldsymbol{z}}_{1}( k+1)-\frac{1}{2}{\boldsymbol{z}}_{1}^{\rm{T}}(k){\boldsymbol{z}}_{1}(k) =\\& \frac{1}{2}[{\boldsymbol{x}}_{1}(k)+T{\boldsymbol{R}}(\varphi _{k}){\boldsymbol{x}}_{2}(k)-{\boldsymbol{x}}_{\mathrm{d}}(k+1)]^{2}-\frac{1}{2}{\boldsymbol{z}}_{1}^{\mathrm{T}}(k){\boldsymbol{z}}_{1}(k) \end{split} (6) 选取虚拟控制函数 {\boldsymbol{\alpha }}({k}) 为
{\boldsymbol{\alpha}} (k)=[T{\boldsymbol{R}}(\varphi _{k}){]}^{-1}[-{\boldsymbol{x}}_{1}(k)+{\boldsymbol{x}}_{\rm{d}}(k+1)] (7) 2.2.2 动力学模型控制系统Ⅱ
后续设计的控制器基于多输入多输出(MIMO)非线性紧格式无模型自适应控制方法。在此介绍相关理论。
一般MIMO非线性离散时间系统可表示为
{\boldsymbol{y}}(k+1)={\boldsymbol{f}}({\boldsymbol{u}}(k),\ldots ,{\boldsymbol{u}}(k-n_u),{\boldsymbol{y}}(k),\ldots ,{\boldsymbol{y}}(k-n_{y})) (8) 式中: {\boldsymbol{u}}({k}),{\boldsymbol{y}}({k}) \in {{\bf{R}}^m} ,分别表示系统的输入和输出; \boldsymbol{f} 为未知的非线性向量函数; {n_u} 和 n{_y} 分别为系统未知阶次。
假设1:函数\boldsymbol{f} 对于控制输入 {\boldsymbol{u}}({k}) 的偏导数是连续的。
假设2:对于一般MIMO非线性离散时间控制系统,给定有界期望输出 {{\boldsymbol{y}}^*}({k} + 1) ,必定存在有界控制输入 {\boldsymbol{u}}({k}) 与其对应,系统在控制输入 {\boldsymbol{u}}({k}) 驱动下输出等于期望输出 {{\boldsymbol{y}}^*}({k} + 1) 。
假设3:系统符合广义Lipschitz条件,即对任意时刻 {k} 和 \left\| {\Delta {\boldsymbol{u}}({k})} \right\| \ne 0 ,有
\left\| {\Delta {\boldsymbol{y}}({k} + 1)} \right\| \leqslant {\zeta }\left\| {\Delta {\boldsymbol{u}}({k})} \right\| (9) 式中: \Delta {\boldsymbol{y}}({k} + 1) = {\boldsymbol{y}}({k} + 1) - {\boldsymbol{y}}({k}) ,为两个相邻时刻系统的输出变化; \Delta {\boldsymbol{u}}({k}) = {\boldsymbol{u}}({k}) - {\boldsymbol{u}}({k} - 1) ,为两个相邻时刻的控制输入变化; {\zeta } 为大于0的常数。
定理1[15]:当非线性系统满足上述假设,且对所有时刻 {k} 都有 \left\| {\Delta {\boldsymbol{u}}({k})} \right\| \ne 0 ,则此非线性系统可等价地表示为CFDL数据模型:
{\boldsymbol{y}}({k} + 1) = {\boldsymbol{y}}({k}) + {{\boldsymbol{\phi}} _{{c}} }({k})\Delta {\boldsymbol{u}}({k}) (10) 其中,伪雅可比矩阵 {{\boldsymbol{\phi }}_{{c}} }({k}) 对任意时刻 {k} 有界,且在三自由度的系统中有
{{\boldsymbol{\phi }}_{{c}}}({k}) = \left[ \begin{matrix} {{{\phi }_{11}}({k})}&{{{\phi }_{12}}({k})}&{{{\phi }_{13}}({k})} \\ {{{\phi }_{21}}({k})}&{{{\phi }_{22}}({k})}&{{{\phi }_{23}}({k})} \\ {{{\phi }_{31}}({k})}&{{{\phi }_{32}}({k})}&{{{\phi }_{33}}({k})} \end{matrix} \right] (11) 假设4:伪雅可比矩阵 {{\boldsymbol{\phi }}_{{c}}}({k}) 应满足如下的对角占优矩阵条件:
\left\{ \begin{gathered} \left| {{\phi _{ij}}({k})} \right| \leqslant {\gamma _1} \\ {\gamma _2} \leqslant \left| {{\phi _{ii }}({k})} \right| \leqslant \chi {\gamma _2} \\ \end{gathered} \right. (12) 式中: \chi \ge 1,{\gamma }_{2}>2{\gamma }_{1}(2\chi +1) , i = 1,2,3,j = 1,2,3,i \ne j ; {\gamma _1},{\gamma _2} 为大于0的常数。
由上述可知,无人船离散系统中的动力学模型满足对一般MIMO非线性离散时间系统的假设,可写成CFDL数据模型,有
{{\boldsymbol{x}}_2}({k} + 1) = {{\boldsymbol{x}}_2}({k}) + {{\boldsymbol{\phi }}_{{c}} }({k})\Delta {\boldsymbol{\tau}} ({k}) (13) 设 {{\boldsymbol{y}}^*}({k} + 1) = {\boldsymbol{\alpha }}({k}) ,由控制系统Ⅰ容易得到 {{\boldsymbol{y}}^*}({k}) 为期望的有界函数。
对子系统Ⅱ定义如下控制输入准则函数:
{\boldsymbol{J}}({\boldsymbol{\tau}} ({k})) = {\left\| {{{\boldsymbol{y}}^*}({k} + 1) - {{\boldsymbol{x}}_2}({k} + 1)} \right\|^2} + \lambda {\left\| {{\boldsymbol{\tau }}({k}) - {\boldsymbol{\tau }}({k} - 1)} \right\|^2} (14) 式中, \lambda 为输入量的权重因子,用于限制输入变化量。
将式(13)代入式(14),并对 {\boldsymbol{\tau }}({k}) 求导,令其为0,可得控制器
{\boldsymbol{\tau }}({k}) = {\boldsymbol{\tau }}({k} - 1) + \frac{{\rho {{\boldsymbol{\phi }}_{{c}} }^{\rm{T}}({k})}}{{\lambda + {{\left\| {{{\boldsymbol{\phi }}_{{c}} }({k})} \right\|}^2}}}({\boldsymbol{\alpha}} ({k}) - {{\boldsymbol{x}}_2}({k})) (15) 式中, \rho \in (0,1] ,为控制量变化的步长因子。
注1[16]: {{\boldsymbol{\phi }}_{{c}} }({k}) 的精确值难以获取,因此由其估计算法来近似替代,设估计准则函数为
\begin{split} & {\boldsymbol{J}}({{\boldsymbol{\phi }}_{{c}} }({k})) = {\left\| {\Delta {{\boldsymbol{x}}_2}({k}) - {{\boldsymbol{\phi }}_{{c}} }({k})\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|^2} + \\&\qquad\qquad \mu {\left\| {{{\boldsymbol{\phi }}_{{c}} }({k}) - {{\hat {\boldsymbol{\phi}} }_{{c}} }({k} - 1)} \right\|^2} \end{split} (16) 对 {{\boldsymbol{\phi }}_{{c}} }({k}) 求导,令其等于0,可得PJM更新率为
\begin{split} & \qquad\qquad {{\hat {\boldsymbol{\phi}} }_{{c}} }({k}) = {{\hat {\boldsymbol{\phi}} }_{{c}} }({k} - 1) + \\& \frac{{\sigma (\Delta {{\boldsymbol{x}}_2}({k}) - {{\hat {\boldsymbol{\phi}} }_{{c}}}({k} - 1)\Delta {\boldsymbol{\tau}} ({k} - 1))\Delta {\tau ^{\rm{T}}}({k} - 1)}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau}} ({k} - 1)} \right\|}^2}}} \end{split} (17) 式中: \sigma \in (0,2] 为PJM更新的步长因子; \mu 为PJM更新的权重因子。
初值设定(重置算法)如下:
当 {\rm{sign}}({\hat {\boldsymbol{\phi }}_{ii}}({k})) \ne {\rm{sign}}({\hat {\boldsymbol{\phi }}_{ii}}(1)) ,或者 \left| {{{\hat {\boldsymbol{\phi}} }_{ii}}({k})} \right| < {\gamma _2} 或者 \left| {{{\hat {\boldsymbol{\phi}} }_{ii}}({k})} \right| >\chi {\gamma _2} , i = 1,2,3 时, {\hat {\boldsymbol{\phi }}_{ii}}({k}) = {\hat {\boldsymbol{\phi }}_{ii}}(1) ;
当 {\rm{sign}}({\hat {\boldsymbol{\phi }}_{ij}}({k})) \ne {\rm{sign}}({\hat {\boldsymbol{\phi }}_{ij}}(1)) ,或者 \left| {{{\hat {\boldsymbol{\phi}} }_{ij}}({k})} \right| > {{\gamma }_1} , i,j = 1, 2,3 且 i \ne j 时, {\hat {\boldsymbol{\phi }}_{ij}}({k}) = {\hat {\boldsymbol{\phi }}_{ij}}(1) 。
3. 稳定性分析
3.1 伪雅可比矩阵有界性证明
定义PJM误差:
{\tilde {\boldsymbol{\phi }}_{{c}} }({k}) = {\hat {\boldsymbol{\phi }}_{{c}} }({k}) - {{\boldsymbol{\phi }}_{{c}} }({k}) (18) 令 {\hat {\boldsymbol{\phi }}_c }({k}) = \left[ \begin{matrix} {{{\hat {\boldsymbol{\phi}} }_1}^{\rm{T}}({k})}&{{{\hat {\boldsymbol{\phi}} }_2}^{\rm{T}}({k})}&{{{\hat {\boldsymbol{\phi}} }_3}^{\rm{T}}({k})} \end{matrix} \right] ,其中 {\hat {\boldsymbol{\phi }}_i }({k}) = \left[ \begin{matrix} {{{{\hat {\boldsymbol{\phi}} }}_{i 1}}({k})}&{{{{\hat {\boldsymbol{\phi}} }}_{i 2}}({k})}&{{{{\hat {\boldsymbol{\phi}} }}_{i 3}}({k})} \end{matrix} \right],i = 1,2,3 ,c为常数。则式(17)可写为
\begin{split} & \qquad\qquad\quad{{\hat {\boldsymbol{\phi}} }_i }({k}) = {{\hat {\boldsymbol{\phi}} }_i }({k} - 1) + \\& \frac{{\sigma (\Delta {{\boldsymbol{x}}_{2,i }}({k}) - {{\hat {\boldsymbol{\phi}} }_i }({k} - 1)\Delta {\boldsymbol{\tau}} ({k} - 1))\Delta {\tau ^{\rm{T}}}({k} - 1)}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau}} ({k} - 1)} \right\|}^2}}} \end{split} (19) 式中, \Delta {{\boldsymbol{x}}_{2,i }}({k}) = {{\boldsymbol{\phi }}_i }({k} - 1)\Delta {\boldsymbol{\tau }}({k} - 1) 。将式(19)两端同时减去 {\hat {\boldsymbol{\phi }}_{\mathrm{c}} }({k}) ,可得
\begin{split} & {{\tilde {\boldsymbol{\phi}} }_i }({k}) = {{\tilde {\boldsymbol{\phi}} }_i }({k} - 1) + {{\boldsymbol{\phi }}_i }({k} - 1) - {{\boldsymbol{\phi }}_i }({k}) -\\&\;\;\; \frac{{\sigma {{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)\Delta {\boldsymbol{\tau }}({k} - 1)\Delta {{\boldsymbol{\tau }}^{\rm{T}}}({k} - 1)}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}} \end{split} (20) 由定义知, {{\boldsymbol{\phi }}_{\mathrm{c}} }({k}) 对任意时刻 {k} 有界,即存在常数 c 使得 \left\| {{{\boldsymbol{\phi }}_{{c}} }({k})} \right\| \leqslant c ,故可得
\left\| {{{\boldsymbol{\phi }}_i }({k} - 1) - {{\boldsymbol{\phi }}_i }({k})} \right\| \leqslant 2c (21) 式(20)两边取范数,并将式(21))代入,可得
\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k})} \right\| \leqslant \left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)\left( {{\boldsymbol{I}} - \frac{{\sigma \Delta {\boldsymbol{\tau }}({k} - 1)\Delta {{\boldsymbol{\tau }}^{\rm{T}}}({k} - 1)}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}} \right)} \right\| + 2c (22) 对式(22)右端第1项取平方,可得
\begin{split} & {\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)\left( {{\boldsymbol{I}} - \frac{{\sigma \Delta {\boldsymbol{\tau }}({k} - 1)\Delta {{\boldsymbol{\tau }}^{\rm{T}}}({k} - 1)}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}} \right)} \right\|^2} = {\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)} \right\|^2} + \\&\quad\;\; \left( { - 2 + \frac{{\sigma {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}} \right)\frac{{\sigma {{\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}} \end{split} (23) 当 \sigma \in (0,2] , \mu > 0 时,有
- 2 + \frac{{\sigma {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}} < 0 (24) 由式(23)和式(24)可知,因存在 0 < {d _1} < 1 ,故有
\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)\left( {{\boldsymbol{I}} - \frac{{\sigma \Delta {\boldsymbol{\tau }}({k} - 1)\Delta {{\boldsymbol{\tau }}^{\rm{T}}}({k} - 1)}}{{\mu + {{\left\| {\Delta {\boldsymbol{\tau }}({k} - 1)} \right\|}^2}}}} \right)} \right\| \leqslant {d _1}\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)} \right\| (25) 将式(25)代入式(22),可得
\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k})} \right\| \leqslant {d _1}\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)} \right\| + 2c (26) 即通过递归,可得
\begin{split} & \left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k})} \right\| \leqslant {d _1}\left\| {{{\tilde {\boldsymbol{\phi}} }_i }({k} - 1)} \right\| + 2c \leqslant \cdots \leqslant\\&\qquad {d _1}^{k - 1}\left\| {{{\tilde {\boldsymbol{\phi}} }_i }(1)} \right\| + \frac{{2c (1 - {d _1}^{{k} - 1})}}{{1 - {d _1}}} \end{split} (27) 由式(27),可知 {\tilde {\boldsymbol{\phi }}_i }({k}) 有界即 {\tilde {\boldsymbol{\phi }}_{{c}}}({k}) 有界。结合式(18),可以得到 {\hat {\boldsymbol{\phi }}_{{c}} }({k}) 有界。
3.2 动力学模型跟踪误差收敛性分析
在证明动力学模型跟踪误差 {{\boldsymbol{z}}_2}({k}) 的收敛性时,需要用到如下引理。
引理1[14]:令 {\boldsymbol{A}} = ({a_{ij}}) \in {{\bf{C}}^{n \times n}} ,定义Gerschgorin圆盘如下:
{D_i } = \left\{ {z\left| {\left| {z - {a_{ii}}} \right|} \right. \leqslant \sum\nolimits_{{\text{j = }}1,j \ne i }^n {\left| {{a_{ij}}} \right|} } \right\},{\boldsymbol{z}} \in {\bf{C}},1 \leqslant i \leqslant n (28) 则矩阵A的所有特征根都满足 {z_i } \in {D_A} = \bigcup\limits_{i = 1}^n {{D_i }} 。
在动力学模型满足假设1~假设4的条件下,定义跟踪误差为
{{\boldsymbol{z}}_2}({k}) = {{\boldsymbol{y}}^*}({k}) - {{\boldsymbol{x}}_2}({k}) (29) 则可得
\begin{split} & \quad\qquad{{\boldsymbol{z}}_2}({k} + 1) = {{\boldsymbol{y}}^*}({k} + 1) - {{\boldsymbol{x}}_2}({k} + 1) =\\& {{\boldsymbol{y}}^*}({k} + 1) - {{\boldsymbol{y}}^*}({k}) + {{\boldsymbol{y}}^*}({k}) - {{\boldsymbol{x}}_2}({k}) - {{\boldsymbol{\phi }}_{{c}} }({k})\Delta {\boldsymbol{\tau }}({k}) = \\&\qquad\quad \Delta {{\boldsymbol{y}}^*}({k} + 1) + {{\boldsymbol{z}}_2}({k}) - {{\boldsymbol{\phi }}_{{c }}}({k})\Delta {\boldsymbol{\tau }}({k}) \end{split} (30) 将式(15)和式(29)代入式(30),可得
{{\boldsymbol{z}}_2}({k} + 1) = \left( {{{\boldsymbol{z}}_2}({k}) + \Delta {{\boldsymbol{y}}^*}({k} + 1)} \right)\left( {{\boldsymbol{I}} - \frac{{\rho {{\boldsymbol{\phi }}_{{c}} }({k}){{\hat {\boldsymbol{\phi}} }_{{c}} }^{\rm{T}}({k})}}{{\lambda + {{\left\| {{{\hat {\boldsymbol{\phi}} }_{{c}} }({k})} \right\|}^2}}}} \right) (31) 由引理1,可得
\begin{gathered} {D_j } = \\ \left\{ {z\left| z \right. \leqslant \displaystyle\sum\limits_{l = 1,l \ne j }^3 {\frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{li}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{\mathrm{c}} }({k})} \right\|}^2}}} + \left| {1 - \frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{ji}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{\mathrm{c}} }({k})} \right\|}^2}}}} \right|} } \right\} \end{gathered} (32) 式中: {{z}} 为矩阵 {\boldsymbol{I}} - \dfrac{{\rho {{\boldsymbol{\phi }}_c }({k}){{\hat {\boldsymbol{\phi}} }_c }^{\rm{T}}({k})}}{{\lambda + {{\left\| {{{\hat {\boldsymbol{\phi}} }_c }({k})} \right\|}^2}}} 的特征根; {D_j } 为Gerschgorin圆盘。
由重置算法,知 {\gamma _2} \leqslant \left| {{{\hat {\boldsymbol{\phi}} }_{ii}}({k})} \right| \leqslant \chi {\gamma _2} , \left| {{{\hat {\boldsymbol{\phi}} }_{ij}}({k})} \right| \leqslant {\gamma _1} 。又由假设4,知 {\gamma _2} \leqslant \left| {{{\boldsymbol{\phi }}_{ii}}({k})} \right| \leqslant \chi {\gamma _2} 和 \left| {{{\boldsymbol{\phi }}_{ij}}({k})} \right| \leqslant {\gamma _1} 。
因此,下面2个不等式成立:
1 - \frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{li}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_c }({k})} \right\|}^2}}} \leqslant 1 - \frac{{\rho {\gamma _2}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_c }({k})} \right\|}^2}}} (33) \sum\limits_{l = 1,l \ne j }^3 {\frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{li}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_c }({k})} \right\|}^2}}}} \leqslant \rho \frac{{4\chi {\gamma _1}{\gamma _2} + 2{\gamma _1}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_c }({k})} \right\|}^2}}} (34) 由假设4可知: {\gamma _2} > 2{\gamma _1}(2\chi + 1) ,将式(33)和式(34)相加,可得
\begin{split} & 1 - \frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{li}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} + \sum\limits_{h = 1,l \ne j }^3 {\frac{{{\rho }\displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{hi}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}}} <\\&\qquad\qquad\;\; 1 - \rho \frac{{8\chi {\gamma _1}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} \end{split} (35) 由重置算法和假设4知: {\hat {\boldsymbol{\phi }}_{ji}}({k}){\hat {\boldsymbol{\phi }}_{ji}}({k}) > 0 。因此存在一个 {\lambda _{\min }} > 0 使得 \lambda > {\lambda _{\min }} ,下式成立。
\begin{split} & \frac{{\displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{ji}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} = \frac{{\displaystyle\sum\limits_{i = 1}^3 {\left| {{{\boldsymbol{\phi }}_{ji}}({k})} \right|\left| {{{\hat {\boldsymbol{\phi}} }_{ji}}({k})} \right|} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} \leqslant\\&\;\;\;\;\;\; \frac{{{\chi ^2}{\gamma _2}^2 + 2{\gamma _1}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} < \frac{{{\chi ^2}{\gamma _2}^2 + 2{\gamma _1}^2}}{{{\lambda _{\min }} + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} < 1 \end{split} (36) 对于式(36),可以选择 0 < \rho \le 1和\lambda > \lambda_{\mathrm{min}} ,使得
\left| {1 - \frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{ji}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}}} \right| = 1 - \frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {\left| {{{\boldsymbol{\phi }}_{ji}}({k})} \right|\left| {{{\hat {\boldsymbol{\phi}} }_{ji}}({k})} \right|} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} (37) 对于任意 \lambda > {\lambda _{\min }} ,有
\begin{split} & 0 < {M_1} \leqslant \frac{{8\chi {\gamma _1}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} < \frac{{{\gamma _2}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} \leqslant \\&\quad \frac{{{\chi ^2}{\gamma _2}^2 + 2{\gamma _1}^2}}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} < \frac{{{\chi ^2}{\gamma _2}^2 + 2{\gamma _1}^2}}{{{\lambda _{\min }} + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}} < 1 \end{split} (38) 由式(35)、式(37)和式(38),可知
\begin{split} & \left| {1 - \frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{ji}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}}} \right| + \sum\limits_{l = 1,l \ne j }^{{m}} {\left| {\frac{{\rho \displaystyle\sum\limits_{i = 1}^3 {{{\boldsymbol{\phi }}_{ji}}({k}){{\hat {\boldsymbol{\phi}} }_{li}}({k})} }}{{\lambda + {{\left\| {{{{\hat {\boldsymbol{\phi}} }}_{{c}} }({k})} \right\|}^2}}}} \right|} < \\&\qquad\qquad\qquad 1 - \rho {M_1} < 1 \end{split} (39) 由式(32)和式(39),可知
s \left( {{\boldsymbol{I}} - \frac{{\rho \cdot {{\boldsymbol{\phi }}_c}({k}) \cdot {{\hat {\boldsymbol{\phi}} }_{{c}}}^{\rm{T}}({k})}}{{\lambda + {{\left| {{{\hat {\boldsymbol{\phi}} }_{{c}}}({k})} \right|}^2}}}} \right) < 1 - \rho {M_1} (40) 式中, s \left( {\boldsymbol{U}} \right) 为矩阵U的谱半径,即 s \left( {\boldsymbol{U}} \right) = \mathop {\max }\limits_{i \in \left\{ {1,2, \ldots ,m} \right\}} \left| {{z_i }} \right| {z_i }, i = 1, 2, \ldots ,m ,为矩阵特征值。
由谱半径的结论,可知存在任意小数 \varepsilon ,使得
\begin{split} & {\left\| {{\boldsymbol{I}} - \frac{{\rho \cdot {{\boldsymbol{\phi }}_c }({k}) \cdot {{\hat {\boldsymbol{\phi}} }_c }^{\rm{T}}({k})}}{{\lambda + {{\left| {{{\hat {\boldsymbol{\phi}} }_c }({k})} \right|}^2}}}} \right\|_{v}} < s \left( {{\boldsymbol{I}} - \frac{{\rho \cdot {{\boldsymbol{\phi }}_c }({k}) \cdot {{\hat {\boldsymbol{\phi}} }_c }^{\rm{T}}({k})}}{{\lambda + {{\left| {{{\hat {\boldsymbol{\phi}} }_c }({k})} \right|}^2}}}} \right) \leqslant \\&\qquad\qquad\quad 1 - \rho {M_1} + \varepsilon < 1 \end{split} (41) 式中, {\left\| {\boldsymbol{U}} \right\|_{v}} 为矩阵{\boldsymbol{U}} 的相容范数。
因 {{\boldsymbol{y}}^*}({k}) 为期望的有界函数,故存在正数 {d _2} ,使得 \left\| {\Delta {{\boldsymbol{y}}^*}({k} + 1)} \right\| < {d _2} 。
令 {d _3} = 1 - \rho {M_1} + \varepsilon < 1 ,并对式(31)取范数,可得
\begin{gathered} {\left\| {{{\boldsymbol{z}}_2}({k} + 1)} \right\|_{v}} \leqslant \\ \left( {{{\left\| {{{\boldsymbol{z}}_2}({k})} \right\|}_{v}} + {{\left\| {\Delta {{\boldsymbol{y}}^*}({k} + 1)} \right\|}_{v}}} \right){\left\| {I - \frac{{\rho {{\boldsymbol{\phi }}_{{c}} }({k}){{\hat {\boldsymbol{\phi}} }_{{c }}}^{\rm{T}}({k})}}{{\lambda + {{\left\| {{{\hat {\boldsymbol{\phi}} }_{{c}} }({k})} \right\|}^2}}}} \right\|_{v}} \leqslant \\ {d _3}{\left\| {{{\boldsymbol{z}}_2}({k})} \right\|_{v}} + {d _2}{d _3} \leqslant \cdots \leqslant {d _3}^{k}{\left\| {{{\boldsymbol{z}}_2}(1)} \right\|_{v}} + \frac{{{d _2}{d _3} - {d _2}{d _3}^{k}}}{{1 - {d _3}}} \end{gathered} (42) 并得到
\mathop {\lim }\limits_{{k} \to \infty } {\left\| {{{\boldsymbol{z}}_2}({k} + 1)} \right\|_{v}} = \frac{{{d _2}{d _3}}}{{1 - {d _3}}} (43) 即 {{\boldsymbol{z}}_2}({k}) 收敛。
3.3 运动学模型跟踪误差收敛性分析
由式(2)和式(18),可得
\begin{split} & \quad{{\boldsymbol{z}}_1}({k} + 1) = {{\boldsymbol{x}}_1}({k} + 1) - {{\boldsymbol{x}}_{\rm{d}}}({k} + 1) =\\&\quad {{\boldsymbol{x}}_1}({k}) + T{\boldsymbol{R}}({\varphi _{k}}){{\boldsymbol{x}}_2}({k}) - {{\boldsymbol{x}}_{\rm{d}}}({k} + 1) = \\& {{\boldsymbol{x}}_1}({k}) - {{\boldsymbol{x}}_{\rm{d}}}({k} + 1) + T{\boldsymbol{R}}({\varphi _{k}})({{\boldsymbol{y}}^*}({k}) - {{\boldsymbol{z}}_2}({k})) \end{split} (44) 代入式(7),可得
{{\boldsymbol{z}}_1}({k} + 1) = T{\boldsymbol{R}}({\varphi _{k}})({{\boldsymbol{y}}^*}({k}) - {{\boldsymbol{y}}^*}({k} + 1) - {{\boldsymbol{z}}_2}({k})) (45) 两边取模,可得
\begin{gathered} \left\| {{{\boldsymbol{z}}_1}({k} + 1)} \right\| \leqslant \left\| {T{\boldsymbol{R}}({\varphi _{k}})} \right\| \cdot \left\| {{{\boldsymbol{y}}^*}({k}) - {{\boldsymbol{y}}^*}({k} + 1) - {{\boldsymbol{z}}_2}({k})} \right\| \leqslant\\ \left\| {T{\boldsymbol{R}}({\varphi _{k}})} \right\| \cdot \left\{ {\left\| {{{\boldsymbol{y}}^*}({k}) - {{\boldsymbol{y}}^*}({k} + 1)} \right\| + \left\| {{{\boldsymbol{z}}_2}({k})} \right\|} \right\} \end{gathered} (46) 又因 \left\| {T{\boldsymbol{R}}({\varphi _{k}})} \right\| \leqslant 1 , \left\| {\Delta {{\boldsymbol{y}}^*}({k} + 1)} \right\| < {d _2} 且 \left\| {{{\boldsymbol{z}}_2}({k})} \right\| 收敛,故由函数收敛判定准则知 {{\boldsymbol{z}}_1}({k}) 收敛。
4. 仿真验证
基于数据驱动的无人船轨迹跟踪控制仿真,验证所提控制算法的有效性。
系统仿真参数如表1 [17] 所示。表中:ρ为控制量变化的步长因子;λ为输入量的权重因子,用来限制输入变化量; σ为PJM更新的步长因子;μ为PJM更新的权重因子。
取采样时间 T = 0.01{\text{ s}} 。根据一般性,设无人船的时变扰动如下:
{\boldsymbol{d}} = \left[ \begin{matrix} {2.3 + 3\sin (0.1{{t}}) + 4\sin(0.02{{t}})} \\ { - 1.9 + 4\sin (0.02{{t}} - {{\text{π}} }/6) + 3\sin(0.3{{t}})} \\ { - 4\sin (0.01{{t}}) - \sin(0.09{{t}} + {{\text{π}} }/3)} \end{matrix} \right] (47) 为提升仿真实验的代表性,期望轨迹选取折线轨迹与圆形轨迹开展仿真。
4.1 折线期望轨迹仿真
取无人船折线期望轨迹:
\left\{ \begin{aligned} & {{\boldsymbol{x}}_{\rm{d}} } = {{\left[ \begin{matrix} {\dfrac{t}{{80}}}&{\dfrac{t}{{80}}}&{\dfrac{{\text{π }}}{4}} \end{matrix} \right]}^{\rm{T}}},&& t < 400{\text{ s }} \\ & {{\boldsymbol{x}}_{\rm{d}} } = {{\left[ \begin{matrix} {\dfrac{t}{{80}}}&{13 - \dfrac{t}{{50}}}&{ - \dfrac{{\text{π }}}{4}} \end{matrix} \right]}^{\rm{T}}},&& 400{\text{ s}} < t < 800{\text{ s}} \end{aligned} \right. (48) 无人船初始位置和速度分别选择为:
{{\boldsymbol{x}}_1}(0) = {\left[ \begin{matrix} 3&1&0 \end{matrix} \right]^{\rm{T}}} , \;\;{{\boldsymbol{x}}_2}(0) = {\left[ \begin{matrix} 0&0&0 \end{matrix} \right]^{\rm{T}}} (49) 4.2 圆形期望轨迹仿真
期望轨迹采用Wang等[18]在无人船轨迹跟踪研究中的期望轨迹:
\begin{split} & {\boldsymbol{x}}_{\rm{d}} =\left[{6} - 5\cos\left(\frac{{\text{π}}t}{{180}}\right)\;\; - {0}.5+2\sin\left(\frac{{\text{π}}t}{{180}}\right)\;\; \frac{{\text{π}}}{{2}}\cos\left(\frac{{\text{π}}t}{{180}}\right)\right]^{\rm{T}}\\[-10pt]&\; \end{split} (50) 无人船初始位置和速度分别选择为:
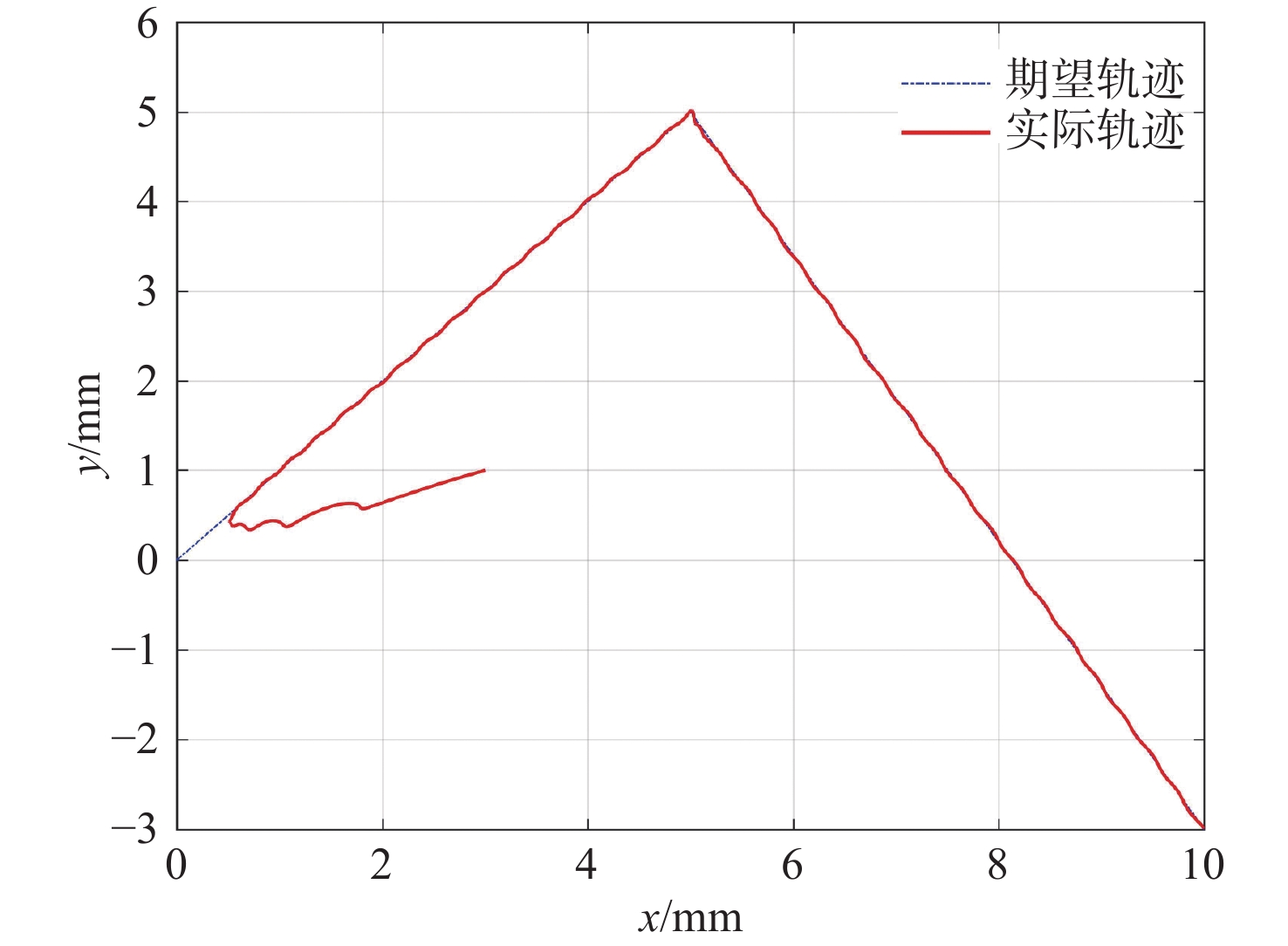
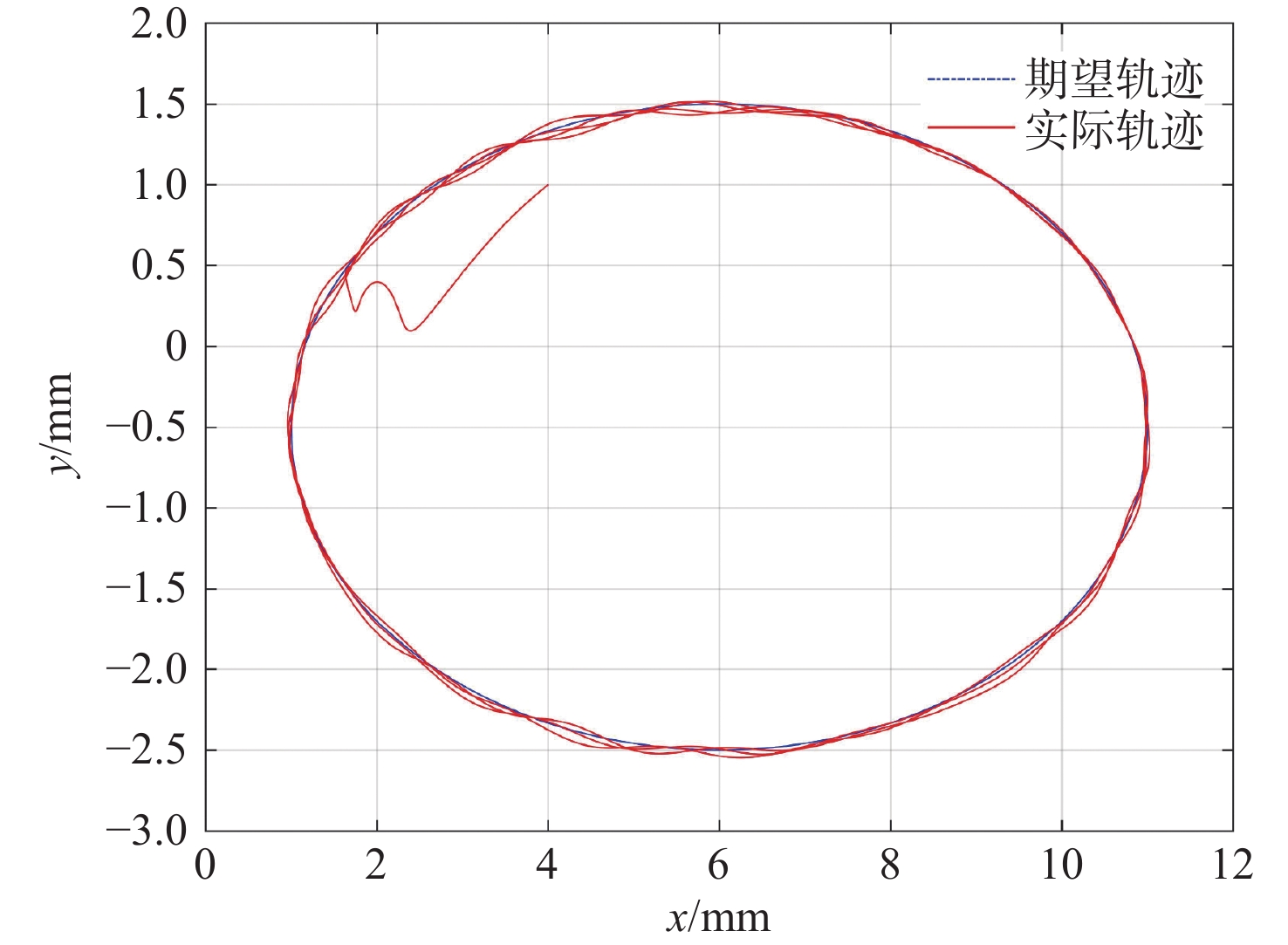
{{\boldsymbol{x}}_1}(0) = {\left[ \begin{matrix} 4&1&0 \end{matrix} \right]^{\rm{T}}} ,\;\; {{\boldsymbol{x}}_2}(0) = {\left[ \begin{matrix} 0&0&0 \end{matrix} \right]^{\rm{T}}} (51) 图2和图7所示为无人船在二维平面下的运动轨迹曲线,可以看出无人船从初始位置出发后,能够以较小的误差沿期望轨迹行驶。
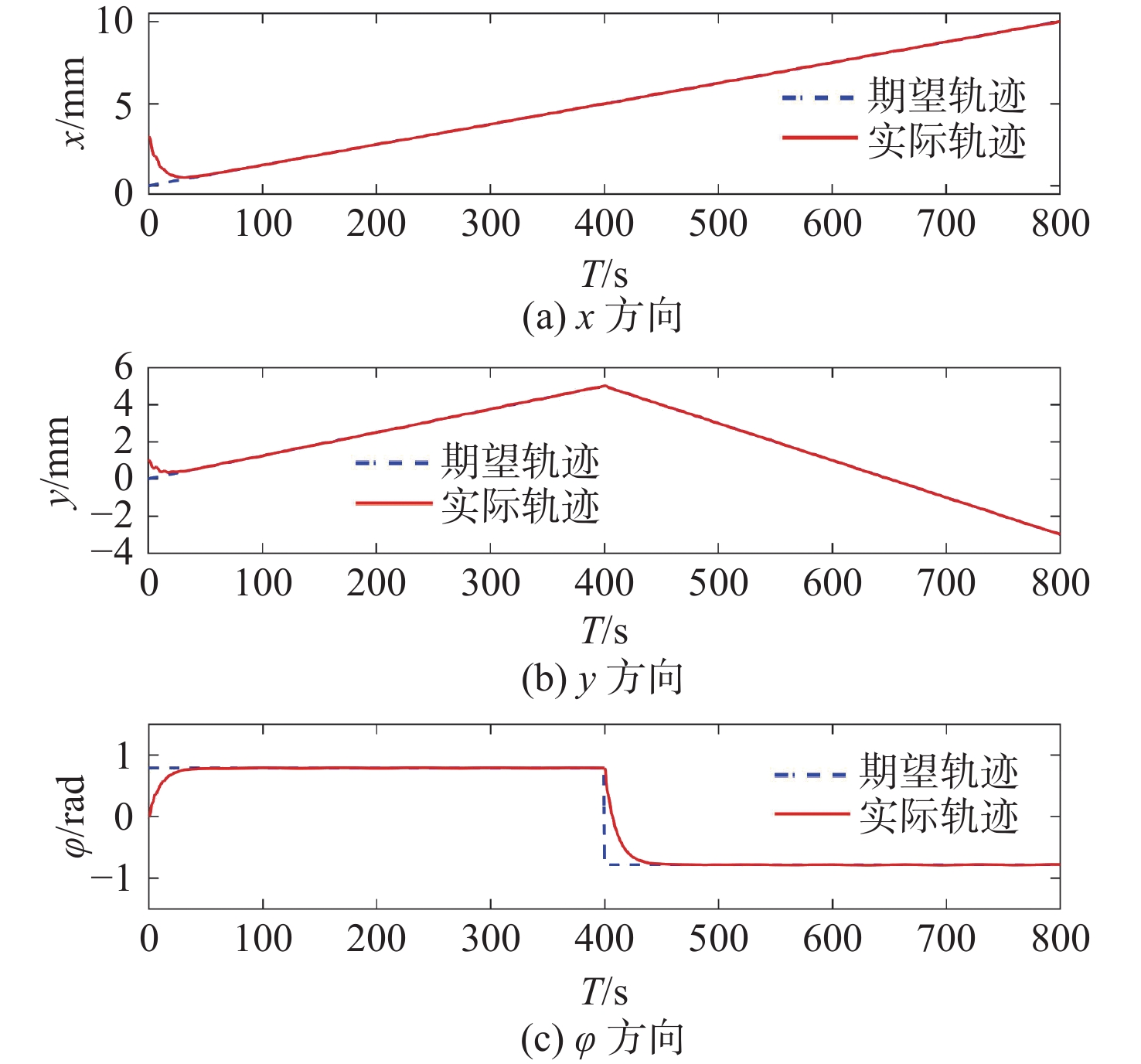
图3和图8所示为控制系统在各个方向的轨迹跟踪情况,经过控制系统调节后,系统的各个方向的曲线逐渐与期望曲线重合,轨迹平滑,可以较好地实现轨迹跟踪。
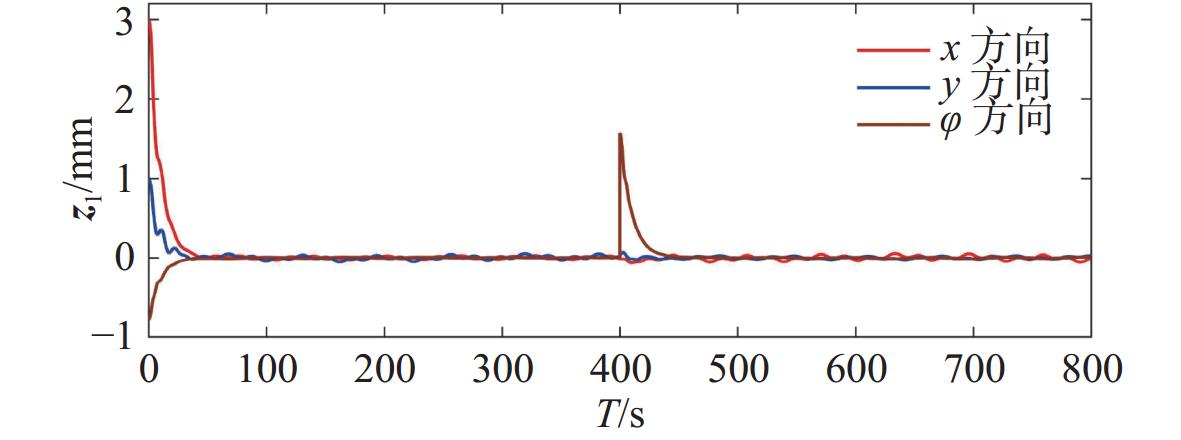
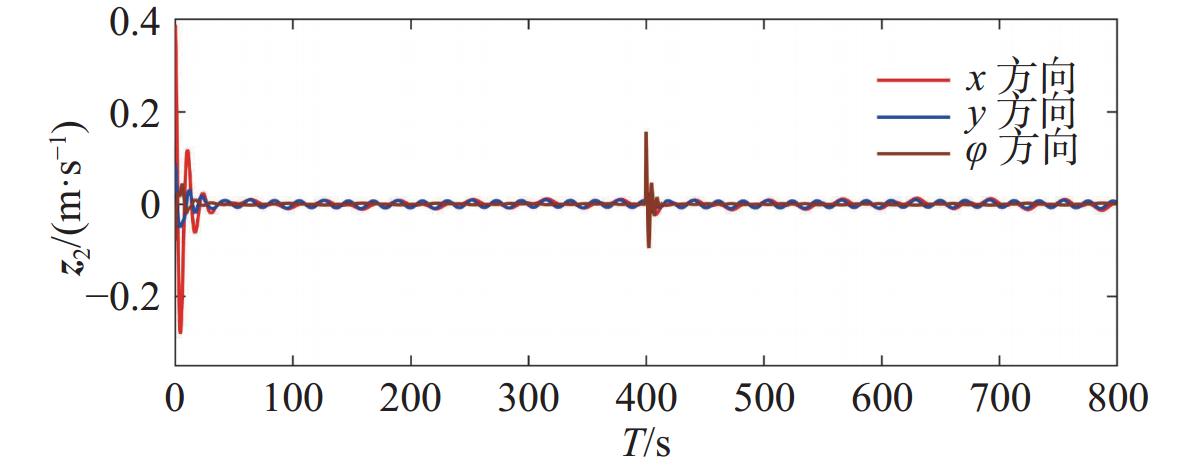
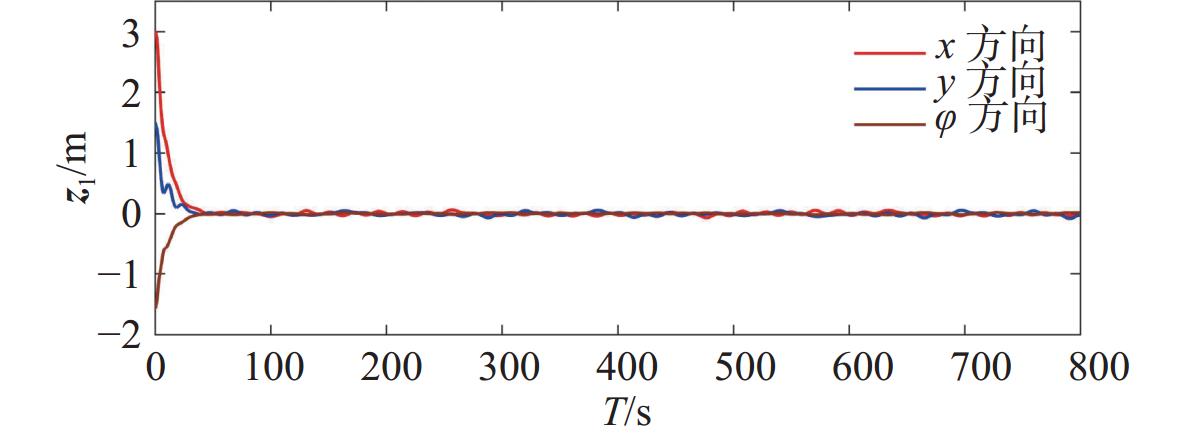
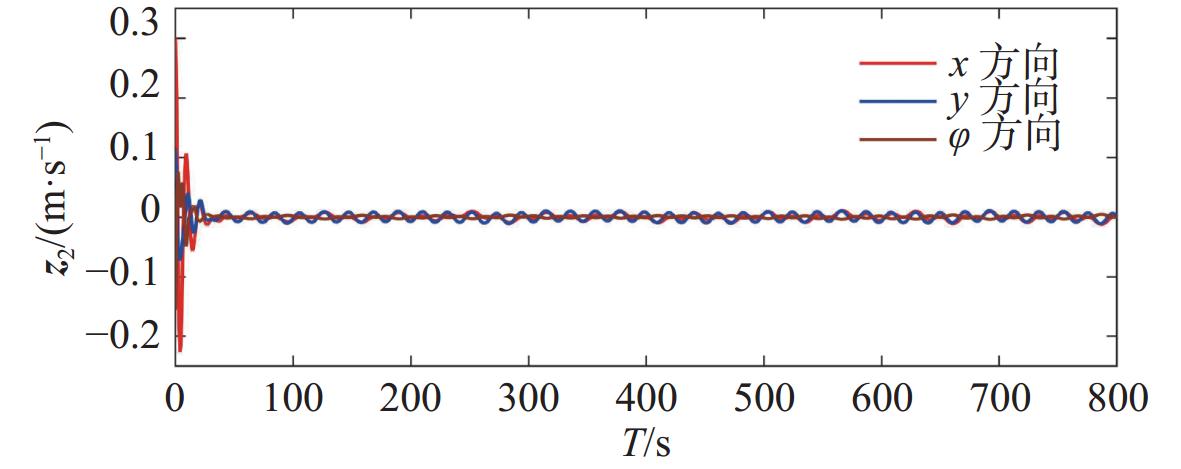
图4和图9所示为运动学子系统Ⅰ的轨迹跟踪误差,即无人船期望轨迹与实际轨迹的误差。图中,运动学子系统的调整时间为30 s,稳态误差为[−0.01 m,0.01 m]。图5和图10所示为动力学子系统Ⅱ的跟踪误差,即无人船期望速度与实际速度的误差。图中,动力学子系统的调整时间为45 s,稳态误差为[−0.05 m,0.05 m]。可以看出,子系统Ⅰ和Ⅱ中三自由度的跟踪误差均能较快收敛且跟踪效果较好。
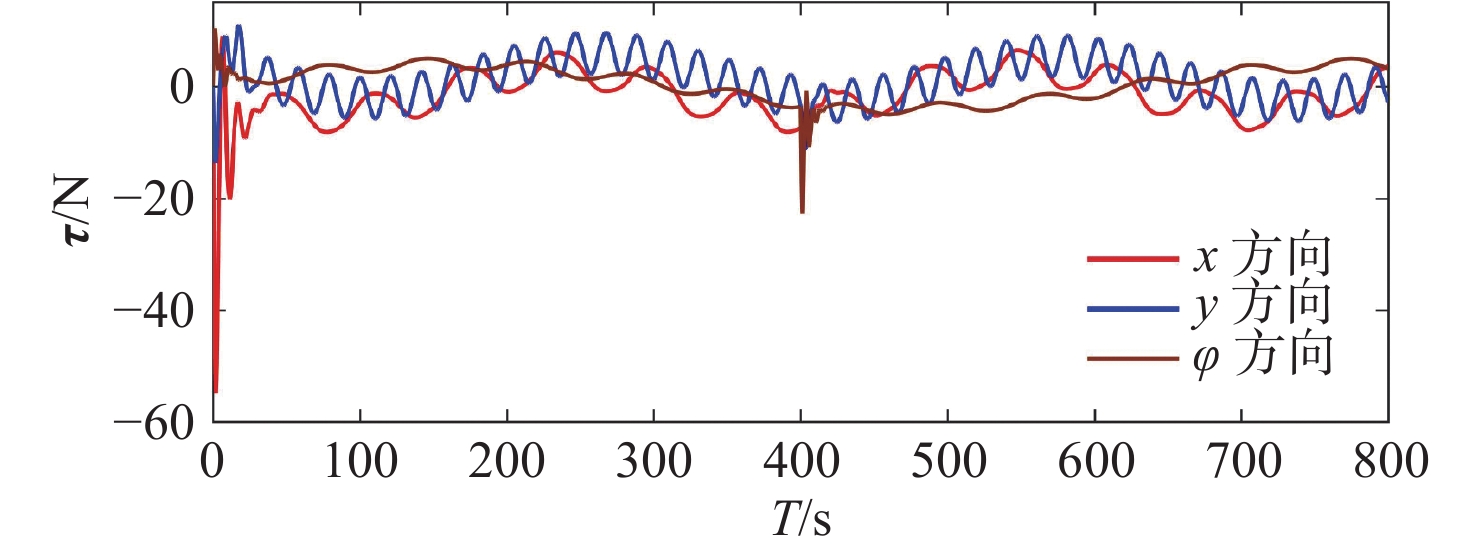
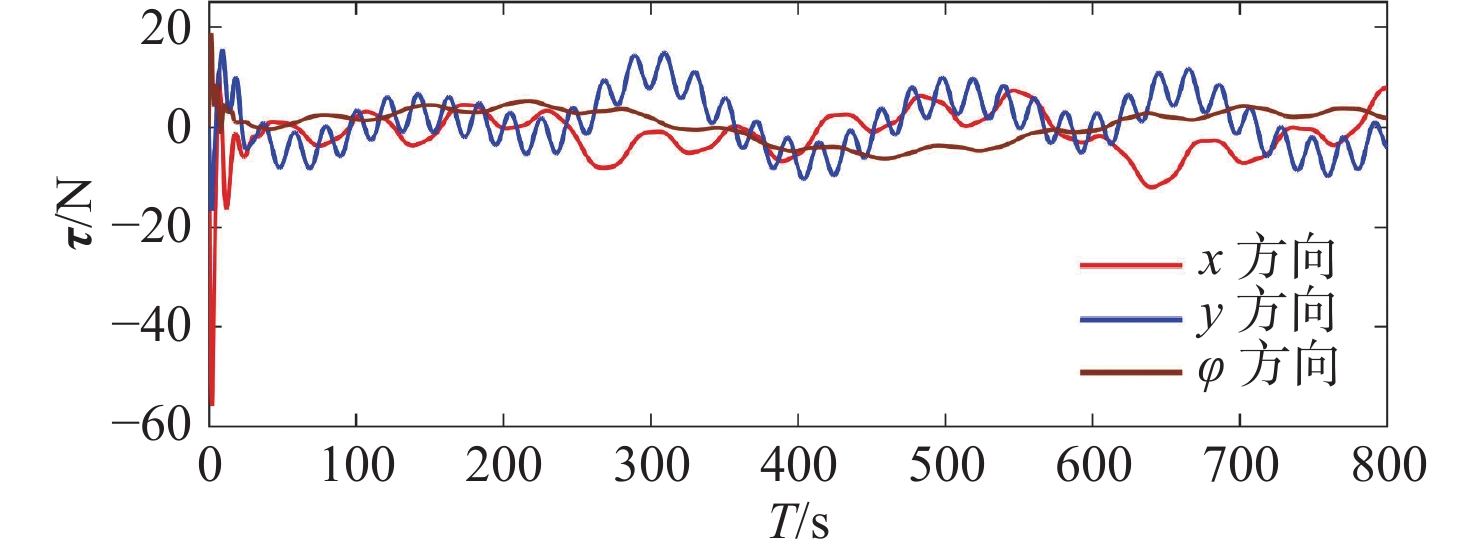
图6和图11为系统的控制器输入曲线。由于前期无人船的实际初始位置与期望轨迹的初始位置有所偏移,轨迹跟踪系统需要输入足够的力矩使得无人船回归期望轨线航行,因此系统控制输入变化较大。无人船航行稳定后,控制输入逐步转变为有界平稳的控制曲线。结合无人船运动轨迹可知,控制输入曲线符合实际情况。
5. 结 论
本文基于反步法提出了一种数据驱动无人船轨迹跟踪控制策略。利用反步法设计无人船运动学模型虚拟控制律,充分利用无人船已有的结构信息,提高系统的跟踪性能,进而采用数据驱动紧格式线性化方法处理无人船动力学模型,降低系统未知参数及时变扰动的影响,实现轨迹跟踪控制器设计。稳定性分析表明,基于数据驱动的无人船轨迹跟踪控制策略可以保证闭环系统的稳定性。仿真结果表明,该控制策略可有效实现系统输出对给定信号的跟踪。此策略主要优点如下:
1) 与传统的无人船反步跟踪策略相比,本文引入基于紧格式动态线性方法,可以有效降低系统中未知模型参数、不确定扰动所造成的影响,具有良好的鲁棒性。
2) 与数据驱动跟踪控制相比,本文控制方案有效利用了无人船模型的结构特点,在简化控制器设计过程的同时保证了系统稳定性。
-
[1] 裴志远, 戴永寿, 李立刚, 等. 无人船运动控制方法综述[J]. 海洋科学, 2020, 44(3): 153–162. doi: 10.11759/hykx20190611004 PEI Z Y, DAI Y S, LI L G, et al. Overview of unmanned surface vehicle motion control methods[J]. Marine Sciences, 2020, 44(3): 153–162 (in Chinese). doi: 10.11759/hykx20190611004
[2] 郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策, 2009, 24(3): 321–329. doi: 10.3321/j.issn:1001-0920.2009.03.001 GUO C, WANG Y, SUN F C, et al. Survey for motion control of underactuated surface vessels[J]. Control and Decision, 2009, 24(3): 321–329 (in Chinese). doi: 10.3321/j.issn:1001-0920.2009.03.001
[3] 关海滨, 艾矫燕. Backstepping法在欠驱动无人船轨迹跟踪上的仿真研究[J]. 中国科技信息, 2018(12): 107–111. doi: 10.3969/j.issn.1001-8972.2018.12.038 GUAN H B, AI J Y. Backstepping control for tracking of unmanned surface vehicle[J]. China Science and Technology Information, 2018(12): 107–111 (in Chinese). doi: 10.3969/j.issn.1001-8972.2018.12.038
[4] 张凯, 王玉龙, 刘兆清. 带扰动观测器的欠驱动水面无人船轨迹跟踪控制[J]. 舰船科学技术, 2019, 41(12): 128–132, 139. doi: 10.3404/j.issn.1672-7649.2019.12.026 ZHANG K, WANG Y L, LIU Z Q. Trajectory tracking control of underactuated unmanned surface vehicles with disturbance observer[J]. Ship Science and Technology, 2019, 41(12): 128–132, 139 (in Chinese). doi: 10.3404/j.issn.1672-7649.2019.12.026
[5] YANG Y, DU J L, LIU H B, et al. A trajectory tracking robust controller of surface vessels with disturbance uncertainties[J]. IEEE Transactions on Control Systems Technology, 2014, 22(4): 1511–1518. doi: 10.1109/TCST.2013.2281936
[6] 张昕. 欠驱动水面无人艇轨迹跟踪的反步滑模控制[J]. 数字技术与应用, 2020, 38(1): 170–173. doi: 10.19695/j.cnki.cn12-1369.2020.01.89 ZHANG X. Backstepping sliding mode control for trajectory tracking of underactuated USV[J]. Digital Technology & Application, 2020, 38(1): 170–173 (in Chinese). doi: 10.19695/j.cnki.cn12-1369.2020.01.89
[7] 邢道奇, 张良欣. 船舶航迹跟踪的滑模控制[J]. 船舶, 2011, 22(5): 10–14. doi: 10.3969/j.issn.1001-9855.2011.05.003 XING D Q, ZHANG L X. Sliding-model control for trajectory tracking of surface vessels[J]. Ship & Boat, 2011, 22(5): 10–14 (in Chinese). doi: 10.3969/j.issn.1001-9855.2011.05.003
[8] CHEN J H, ZHANG Q Y, QI Y, et al. Trajectory tracking based on backstepping sliding mode control for underactuated USV[C]//2021 36th Youth Academic Annual Conference of Chinese Association of Automation (YAC). Nanchang: IEEE, 2021: 294−299.
[9] 冯鑫, 于双和. 基于滑模预测控制的水面无人船轨迹跟踪研究[J]. 电光与控制, 2023, 30(9): 92–98. doi: 10.3969/j.issn.1671-637X.2023.09.016 FENG X, YU S H. Trajectory tracking of unmanned surface vessels based on sliding mode predictive control[J]. Electronics Optics & Control, 2023, 30(9): 92–98 (in Chinese). doi: 10.3969/j.issn.1671-637X.2023.09.016
[10] HOU Z S, WANG Z. From model-based control to data-driven control: survey, classification and perspective[J]. Information Sciences, 2013, 235: 3–35. doi: 10.1016/j.ins.2012.07.014
[11] 廖煜雷, 陈聪聪, 杜廷朋, 等. 变输出无模型自适应无人艇艏向控制方法分析[J]. 中国舰船研究, 2024, 19(1): 75–83. doi: 10.19693/j.issn.1673-3185.02989 LIAO Y L, CHEN C C, DU T P, et al. The research of variable output model-free adaptive heading control method of unmanned surface vehicle[J]. Chinese Journal of Ship Research, 2024, 19(1): 75–83 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.02989
[12] 李诗杰, 徐诚祺, 刘佳仑, 等. 船舶自抗扰无模型自适应航迹控制[J]. 中国舰船研究, 2024, 19(1): 280–289. doi: 10.19693/j.issn.1673-3185.03226 LI S J, XU C Q, LIU J L, et al. Tracking control of ships based on ADRC-MFAC[J]. Chinese Journal of Ship Research, 2024, 19(1): 280–289 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.03226
[13] WENG Y P, WANG N. Data-driven robust backstepping control of unmanned surface vehicles[J]. International Journal of Robust and Nonlinear Control, 2020, 30(9): 3624–3638. doi: 10.1002/rnc.4956
[14] WANG N, GAO Y, ZHANG X F. Data-driven performance-prescribed reinforcement learning control of an unmanned surface vehicle[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12): 5456–5467. doi: 10.1109/TNNLS.2021.3056444
[15] 侯忠生, 金尚泰. 无模型自适应控制: 理论与应用[M]. 北京: 科学出版社, 2013: 92−95. HOU Z S, JIN S T. Model-free adaptive control: theory and applications[M]. Beijing: Science Press, 2013: 92−95 (in Chinese).
[16] HOU Z S, JIN S T. Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems[J]. IEEE Transactions on Neural Networks, 2011, 22(12): 2173–2188. doi: 10.1109/TNN.2011.2176141
[17] 王昱棋, 李铁山. 欠驱动水面船舶的有限时间航迹跟踪控制[J]. 哈尔滨工程大学学报, 2017, 38(5): 684–689. doi: 10.11990/jheu.201512069 WANG Y Q, LI T S. Finite-time trajectory tracking control of under-actuated surface vessel[J]. Journal of Harbin Engineering University, 2017, 38(5): 684–689 (in Chinese). doi: 10.11990/jheu.201512069
[18] WANG N, SUN J C, ER M J, et al. A novel extreme learning control framework of unmanned surface vehicles[J]. IEEE Transactions on Cybernetics, 2016, 46(5): 1106–1117. doi: 10.1109/TCYB.2015.2423635



 下载:
下载: