Experimental and numerical study on water-entry impact of aluminum-plated structure
-
摘要:目的
旨在研究铝合金结构的入水砰击弹塑性响应问题。
方法根据实船底部结构设计一套铝制加筋板缩比模型，通过开展不同高度的结构水平入水砰击试验，分析铝制加筋结构在入水冲击过程中的砰击压力和结构弹塑性动力响应。采用基于任意拉格朗日−欧拉（ALE）算法的显式有限元技术对入水冲击试验模型进行数值模拟。
结果结果表明，平底加筋板砰击时也存在饱和冲量现象，其最终变形量与入水高度之间近似为线性关系，且砰击压力在结构表面具有较好的均匀分布特性。数值预测结果与试验测量结果吻合较好，
结论研究证明了ALE耦合算法对铝制加筋结构入水冲击问题研究的可行性。
Abstract:ObjectiveThis paper aims to study the slamming-induced elasto-plastic response of aluminum structures.
MethodsIn this paper, an aluminum scale model based on the hull structure of a real ship is designed, then drop tests of aluminum stiffened plates with a deadrise angle of 0° are conducted from different drop heights to investigate the slamming pressure and structural dynamic elastoplastic response.Finally, the slamming drop tests are validated by adopting explicit finite element technology based on the Arbitrary Lagrangian-Euler (ALE) algorithm.
ResultsThe test results show that the saturated impulse phenomenon exists, and the final deformation of the stiffened plate is approximately linearly related to the drop height. The slamming pressure acting on the plate can be regarded as uniformly distributed. The numerical predictions are in good agreement with the experimental results.
ConclusionThe study provides experimental data on the aluminum stiffened plate structure design for high-speed aluminum ships and underwater vehicles.
-
0. 引 言
船舶在恶劣海况下航行船体结构不可避免地会受到波浪产生的巨大冲击压力作用。此外，鱼雷空投入水以及水上飞机起降等行为都存在结构高速入水的冲击问题。因此，合理预报入水冲击载荷对海洋航行器结构设计和船舶航行安全至关重要。船首砰击通常发生在航速较高的船舶上，且随着速度的增加，艏部砰击也愈加剧烈；对于大型船舶，在压载条件和极端海况下更容易出现底部砰击，且底部砰击工况下的载荷峰值较大，对局部结构的强度要求更高[1]。因此，针对砰击载荷以及船体局部结构弹塑性动力响应问题的研究得到了国内外学者的广泛关注。Chuang[2-3]分别针对平底板和加筋板结构开展了大量的入水砰击试验，通过分析砰击压力结果发现压力峰值与结构入水冲击速度的平方近似呈线性关系，并总结了砰击压力幅值的预测公式；此外，Chuang[3]首次在平底板入水冲击试验中发现了压缩空气的现象，且由于空气垫的影响导致压力在平底面上近似呈均匀分布特性。Zhu等[4]针对小水线面双体船特征模型进行了一系列入水砰击试验，试验中测量了不同测点处的砰击压力和应变响应，分析显示当冲击角度不为零时砰击压力存在移动现象，并基于有限差分法对结构响应进行了预测。Wang等[5]针对化学品船在不规则波浪中的砰击问题开展了系列模型试验，主要分析波浪中的船舶运动和砰击概率问题，研究砰击压力与冲击速度及波浪参数的关系，最后采用任意拉格朗日−欧拉（ALE）耦合算法对波浪砰击问题进行了数值模拟。针对三维船体艏部砰击载荷问题，于鹏垚等[6]结合耐波性理论和概率分析方法推导了船首外飘设计砰击速度的计算方法，并结合三维落体试验结果分析了规范方法存在的不足。根据现有的研究结果可以发现，当入水角度较小时空气对砰击载荷的影响较大[3, 7]。针对砰击压力及其移动特性等问题缺乏系统的试验或数值研究的现状，Duan等[8]开展了系列的楔形结构落体砰击试验，系统地研究了入水冲击速度、斜升角和结构刚度对砰击压力和压力移动特性的影响，在精确控制了斜升角的前提下得到的结果表明，当斜升角为0°时作用在结构表面的砰击压力近似呈均匀分布，当斜升角大于0.2°时压力存在明显的迁移特性。
为研究砰击载荷作用下船体结构的弹塑性动力响应问题，Jones[9]最早提出一种能够用于预测船体底板砰击损伤的理论计算方法，并与已有的试验结果进行对比，取得了较好的一致性。Faltinsen等[10-11]基于水平梁模型的波浪砰击试验研究了船体湿甲板的入水冲击问题，试验中采集了砰击压力和结构弹性响应结果，并与建立的局部水弹性响应理论预测结果进行了对比验证。Wang等[12]对砰击载荷作用下矩形板的水弹性响应进行了分析。其中，水动力载荷通过Wagner理论模型进行求解，结构的变形基于模态叠加法进行求解，并与有限元数值计算结果吻合较好。任慧龙等[13]将设计砰击脉冲载荷施加在船首有限元模型上，并利用中心差分法对结构动力响应问题进行了数值计算。Zhu等[14]基于模态叠加法建立了移动砰击压力作用下船体板弹性动力响应的理论预测模型，通过将砰击压力简化为矩形脉冲、线性衰减脉冲和指数衰减脉冲载荷形式，研究了脉冲载荷形状和压力迁移速度对船体板动力响应的影响。田阿利等[15]基于非线性有限单元法分析了外飘砰击载荷下SPS（放电等离子烧结）覆层船艏的结构吸能和应力等力学行为，并与传统钢质结构的吸能特性进行了对比分析。结果表明，SPS覆层船首的总体吸能比钢质结构提升了18.2%。
近年来，由于铝合金材料具有比重和弹性模量小、耐腐蚀、易加工和低温性能好等优点，其在高速舰艇和水下航行器中的应用越来越广泛。Mori[16]针对高速船底部铝合金加筋板开展系列的入水冲击试验，分析了加筋平板不同位置处的冲击压力和变形响应结果，并采用理论方法预测了加筋板结构动力响应，与试验结果吻合性较好。骆寒冰等[17]设计铝制楔形体弹性模型，开展了不同落体高度的入水冲击模型试验，得到了不同入水速度下铝制加筋楔形体模型的冲击压力与结构应变响应结果，并基于ALE方法针对试验模型进行了数值仿真计算，所得结果与实验结果吻合较好。Zhu等[18]试验研究了铝合金平板和低碳钢板入水砰击过程中的塑性大变形响应问题，通过对比分析平底板中心点处的砰击压力和应变结果揭示了结构入水冲击过程中的饱和冲量现象，这与前期提出的板在脉冲压力作用下的饱和冲量理论预测一致[19-21]，并指出对砰击载荷作用下船体板的变形预测中考虑饱和冲量的影响将更加合理和准确。随着轻质夹层结构在船体结构设计中的广泛运用，赵飞等[22]利用LS-DYNA软件对夹层板结构在不同入水冲击速度下的砰击压力和塑性动力响应进行了模拟，结果表明，芯层相对密度对砰击压力和结构的变形响应影响最大。Liu等[23]开展了蜂窝铝夹芯板的落体砰击试验，分析了不同位置处的砰击压力时程结果，以及上下面板的塑性变形响应，通过与平板试验结果对比分析，表明蜂窝铝夹层板的抗冲击载荷性能较好。
根据上述文献以及相关研究可以发现，大多数试验研究关注的是砰击载荷幅值与冲击速度的关系以及结构的弹性响应，然而对于砰击载荷下加筋板结构的塑性动力响应研究较少。本文将基于典型实船底部结构设计一套铝制加筋板缩比模型，并开展不同高度的入水砰击试验，基于试验结果分析不同测点处的砰击压力与结构塑性动力响应的关系。最后，基于ALE耦合方法对不同落体高度工况下加筋板入水冲击问题进行数值模拟，并与砰击试验结果进行对比分析。
1. 试验模型及装置
1.1 试验装置及采集仪器
试验采用自主设计建造的落体砰击试验装置，在38 m×3.8 m×1.8 m（长×宽×深）的水池中完成。该试验装置为不锈钢制桁架结构，桁架底部固定于池底，装置内测安装有4根不锈钢圆柱导轨，安装过程中保证导轨垂直向下，试验模型与水平箱体一起固定在装有轴套的滑动装置上，通过轴套沿着导轨下落。试验过程中，通过装置顶部电动卷扬机将试验模型拉升至指定高度，通过关闭电磁铁释放，试验模型连同水平箱体一同自由下落直至入水。试验前可以通过滑动框架上的角度调节装置配合测角仪调节试验模型入水角度，从而保证试验模型能够实现水平入水冲击，试验装置布置如图1所示。
试验中，采用压电石英动态压力测量传感器（PCB）对砰击压力进行测量，传感器量程为690 kPa，压力上升时间≤1 μs；采用振动冲击采集分析系统（M+P）采集冲击压力；采样频率设置为102.4 kHz；使用中航电测仪器股份有限公司120 Ω电阻应变计测量试验板应变数据，应变单元的采集范围为±20 000 με，采集频率为10 kHz。整个试验过程通过DV设备录制。
1.2 铝制加筋平板模型
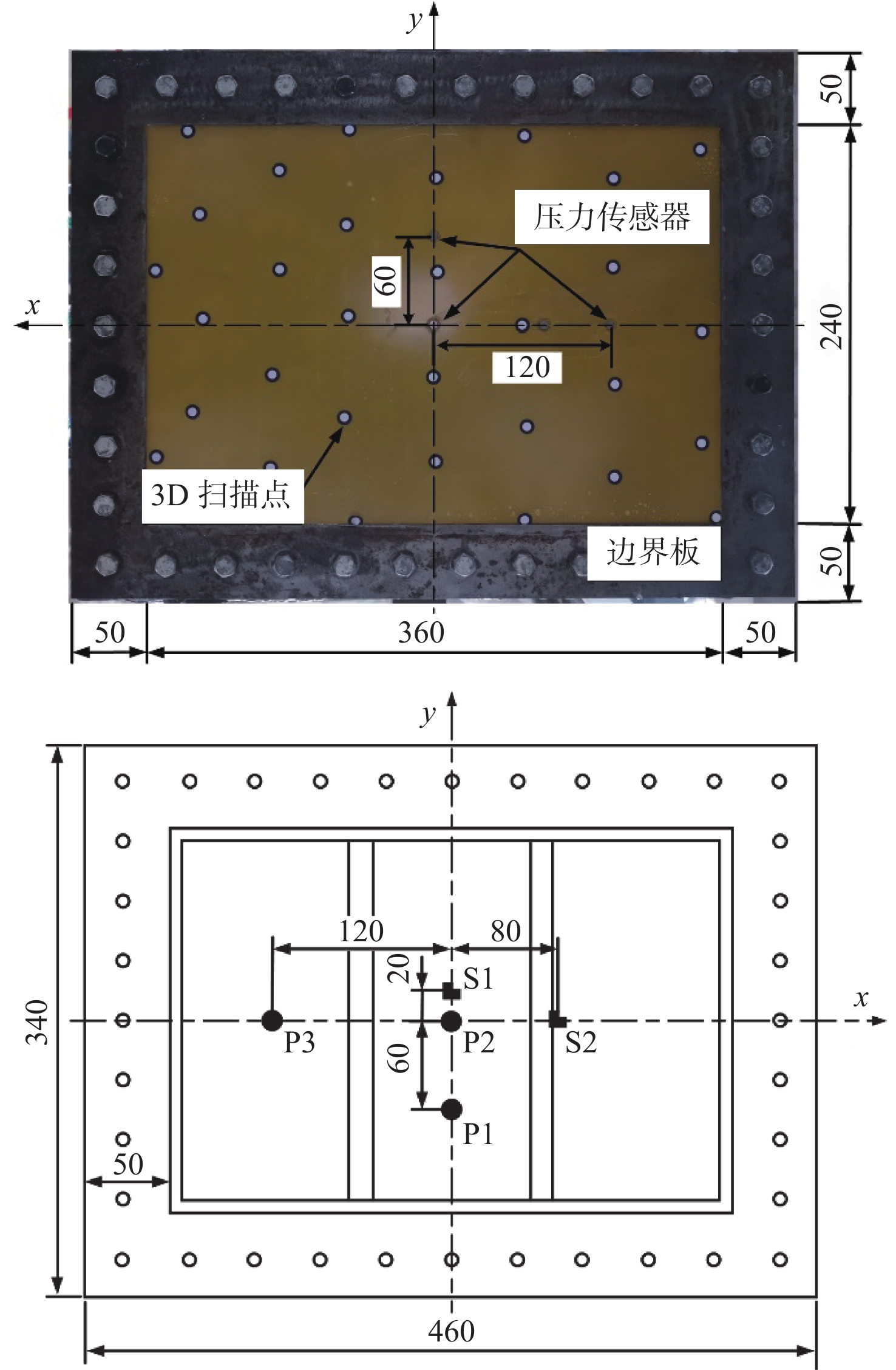
针对实际尺寸为1.8 m×1.2 m的船体底部加筋板架结构，船底板厚度为10.0 mm，基于弗劳德相似准则，缩比得到一组铝合金加筋平板结构模型，结构的柔度系数（β=B/t√σy/E）约为2.96，其中缩尺比取为9。加筋平板模型尺寸为460 mm×340 mm，板厚为2 mm，材料选用5052铝合金，加筋平板模型有效入水冲击区域尺寸为360 mm×240 mm，长宽比3∶2，加强筋尺寸为25 mm×15 mm×2 mm，间距为120 mm。模型分为两个区域，边界固定区域与入水冲击区域。固定区域宽50 mm，在区域内设置间距为40 mm的均布螺栓孔，试验加筋平板与冲击箱体采用螺栓进行装配，并用厚度为2 mm的低碳钢边界板对固定区域进行压紧，以限制试验板的边界沿着螺栓孔向内滑移。加强筋两端焊接在平板有效面积区域的围板侧面，用于模拟加筋两侧的固支边界条件。模型铝合金板采用激光焊接，对板材采用合理的焊接顺序和工艺，以减少焊接变形增强焊接质量，如图2所示。
![]()
图 2 试验加筋平板模型尺寸及测点布置Figure 2. Sizes and measuring points arrangement of testing reinforced flat plate model试验主要测量加筋平板结构入水冲击过程中的入水速度、触水面冲击压力、背水面动态应变以及平板中心最终变形值。由于模型的对称性，压力测点布置在加筋平板左下方四分之一区域，其中P1测点沿y向布置，距中心点60 mm；P2测点布置在加筋平板中心位置；P3测点沿x方向布置，距中心点120 mm。应变测点布置在平板右上方四分之一区域，S1测点沿y方向布置，距中心点20 mm，测量平板中心应变；S2测点沿x方向布置在距中心点80 mm处，测量加强筋焊接处应变，具体布置情况如图2所示。图中数值单位为mm。
2. 试验结果
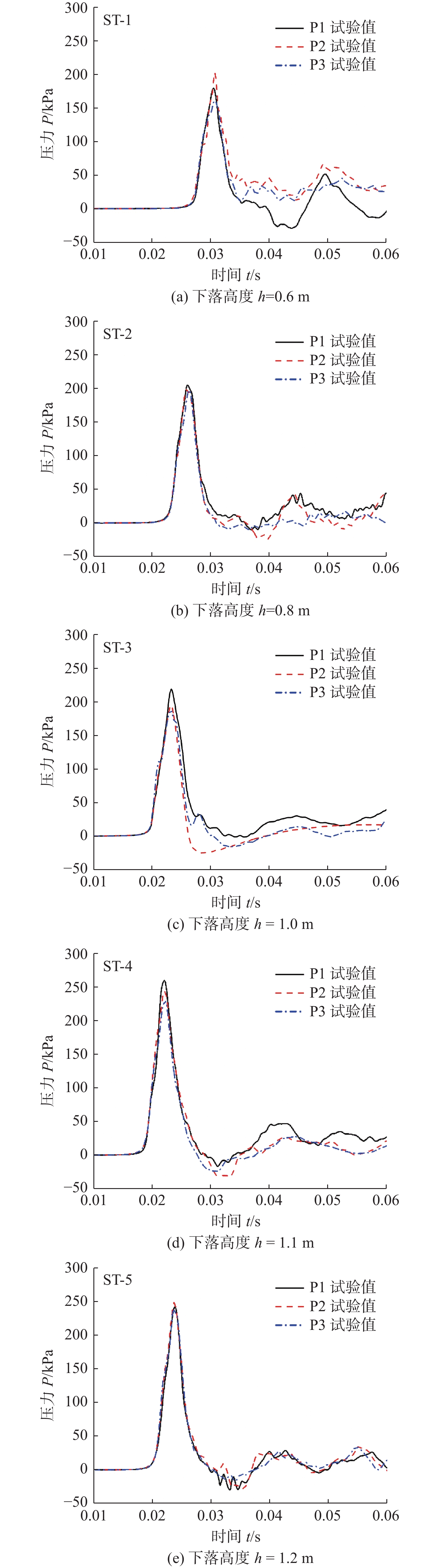
试验包含5个落体高度。为保证测量试验数据的准确性，针对落体高度为0.6 和1.2 m的工况选用4块相同的加筋平板进行了重复试验，试验工况详见表1。此外，表1中给出了不同落体高度工况下结构入水冲击速度的理论计算结果与试验测量结果，可以发现两者的误差很小，表明了本试验装置对入水冲击速度的控制精度较高。每块试验平板均仅进行单次入水冲击试验，试验结束后更换试验板，对模型和传感器等进行检查标定，待水面彻底平静后再进行下一组试验。图3为落体高度为1.2 m时，铝合金加筋平板入水冲击过程，试验中能明显观测到冲击射流现象。
表 1 试验工况表Table 1. Test condition工况
序号下落
高度/m理论入水
速度/(m·s−1)实测入水
速度/(m·s−1)试验
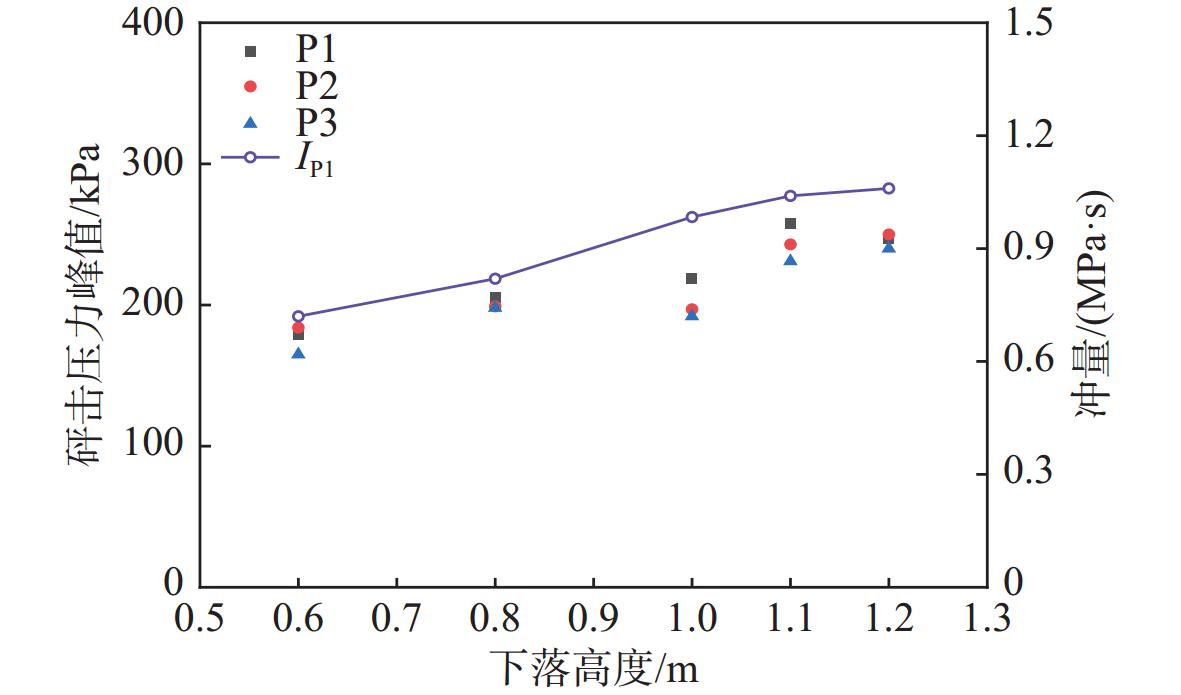
次数ST-1 0.6 3.43 3.36 4 ST-2 0.8 3.96 3.89 1 ST-3 1.0 4.43 4.31 1 ST-4 1.1 4.65 4.54 1 ST-5 1.2 4.85 4.75 4 图4展示了不同下落高度工况下铝合金加筋平板各测点典型入水冲击压力测量曲线。对于不同试验工况，均以试验板下落至水面上方0.1 m时刻为起始时刻。各测点之间冲击压力曲线吻合较好，压力峰值曲线没有出现明显的时间间隔，入水瞬间试验加筋平板未发生倾斜。总体来说，不同测点的压力峰值比较接近，这与Chuang[3]的试验结论较为吻合，这是由于空气垫的影响使得作用在平底结构上砰击压力趋于均匀分布。然而，对于给定的落体高度，可以发现P1，P2和P3测点的压力峰值存在较小的差异，这与板不同测点处的刚度特性以及流固耦合作用都会相关。图5中给出了不同压力测点处的砰击压力峰值随落体高度的变化结果，可以发现，随着落体高度的增加，不同测点处的砰击压力峰值总体上线性上升。此外，图5中还给出了P1测点处的压力冲量IP1随落体高度的变化关系，结果表明，压力冲量结果随着落体高度的增加而增加，其中冲量为图4中压力时程曲线的首个正脉冲积分结果。
![]()
图 4 铝合金加筋平板冲击压力分布Figure 4. Impact pressure distribution of aluminum alloy stiffened plate![]()
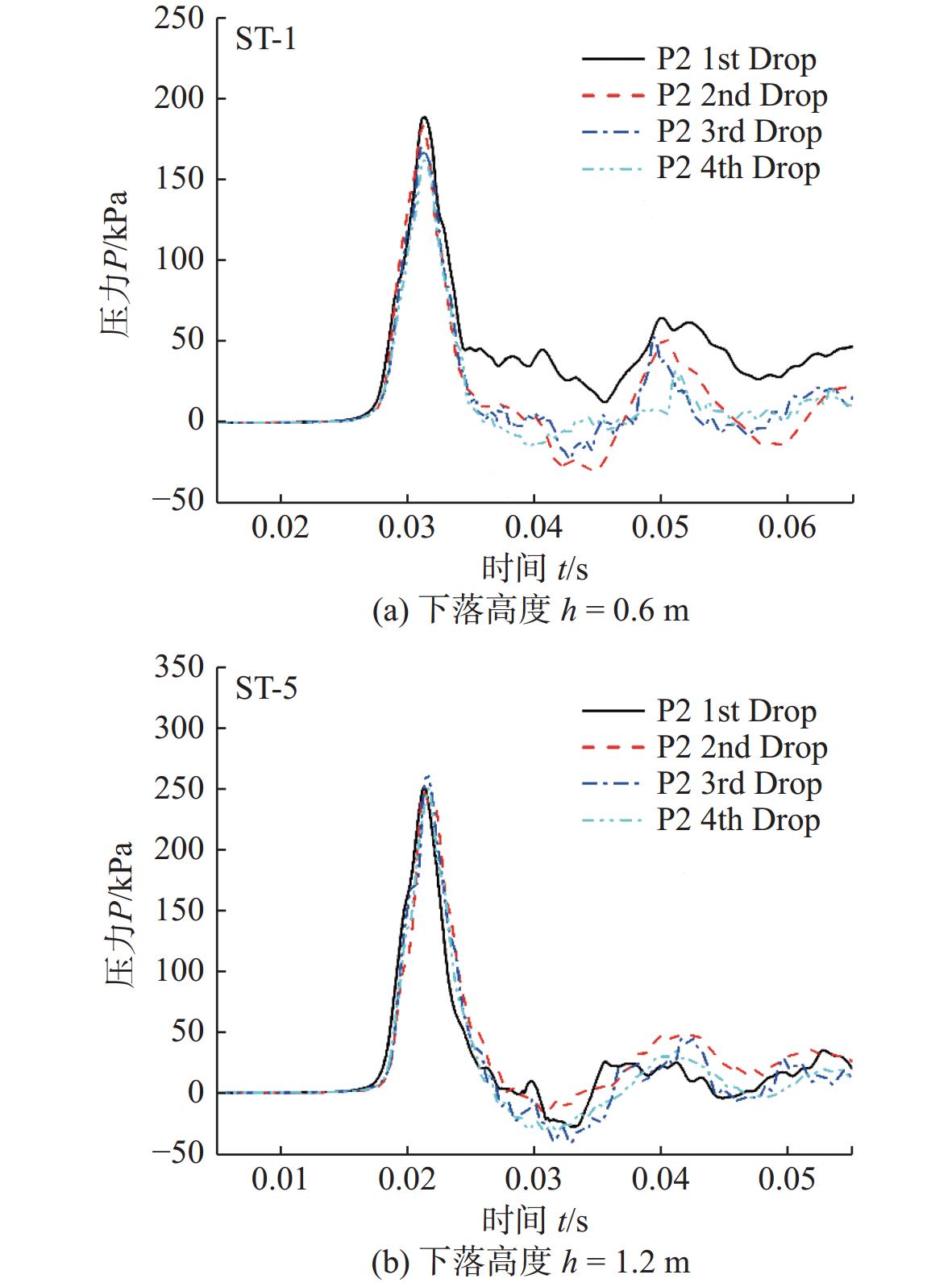
图 5 不同测点处的砰击压力峰值以及P1测点处的压力冲量随落体高度的变化关系Figure 5. Variation of peak slamming pressure at different measuring points and impulse at P1 mearuring point with drop heights of falling body图6为试验模型中心测点P2在0.6 和 1.2 m落体高度下重复试验测量得到的压力峰值曲线数据。可以看出，在相同落体高度下，除少数压力峰值曲线末期出现较大随机性跳跃以外，其他不同加筋平板在同一落体高度下测得的加筋平板冲击压力峰值重复性较好，压力时程曲线吻合度较高，证明了入水冲击实验装置和测量数据的有效性。
![]()
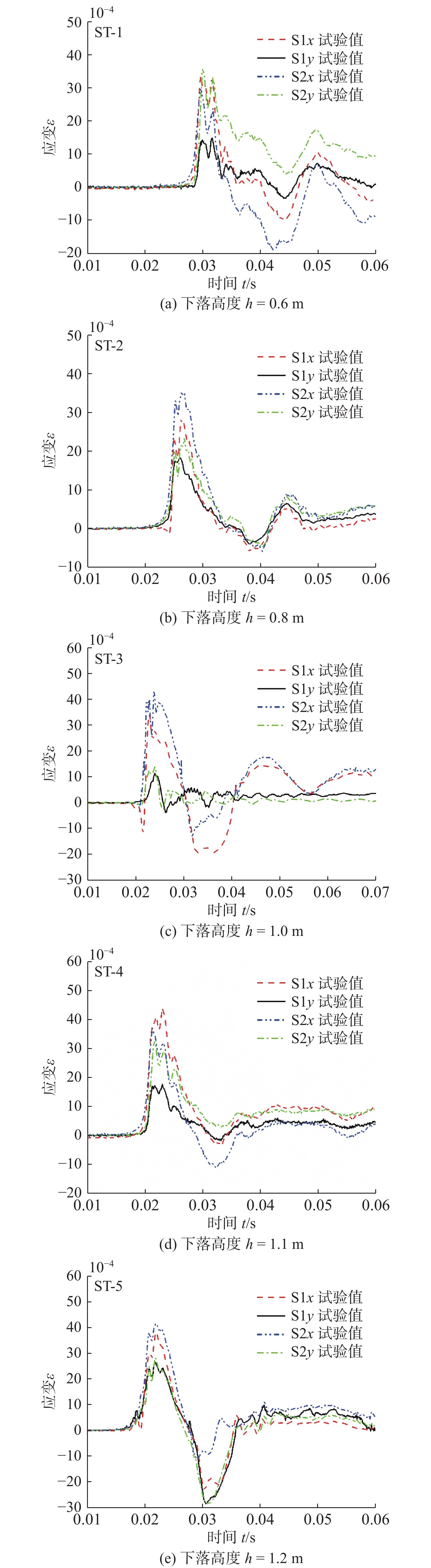
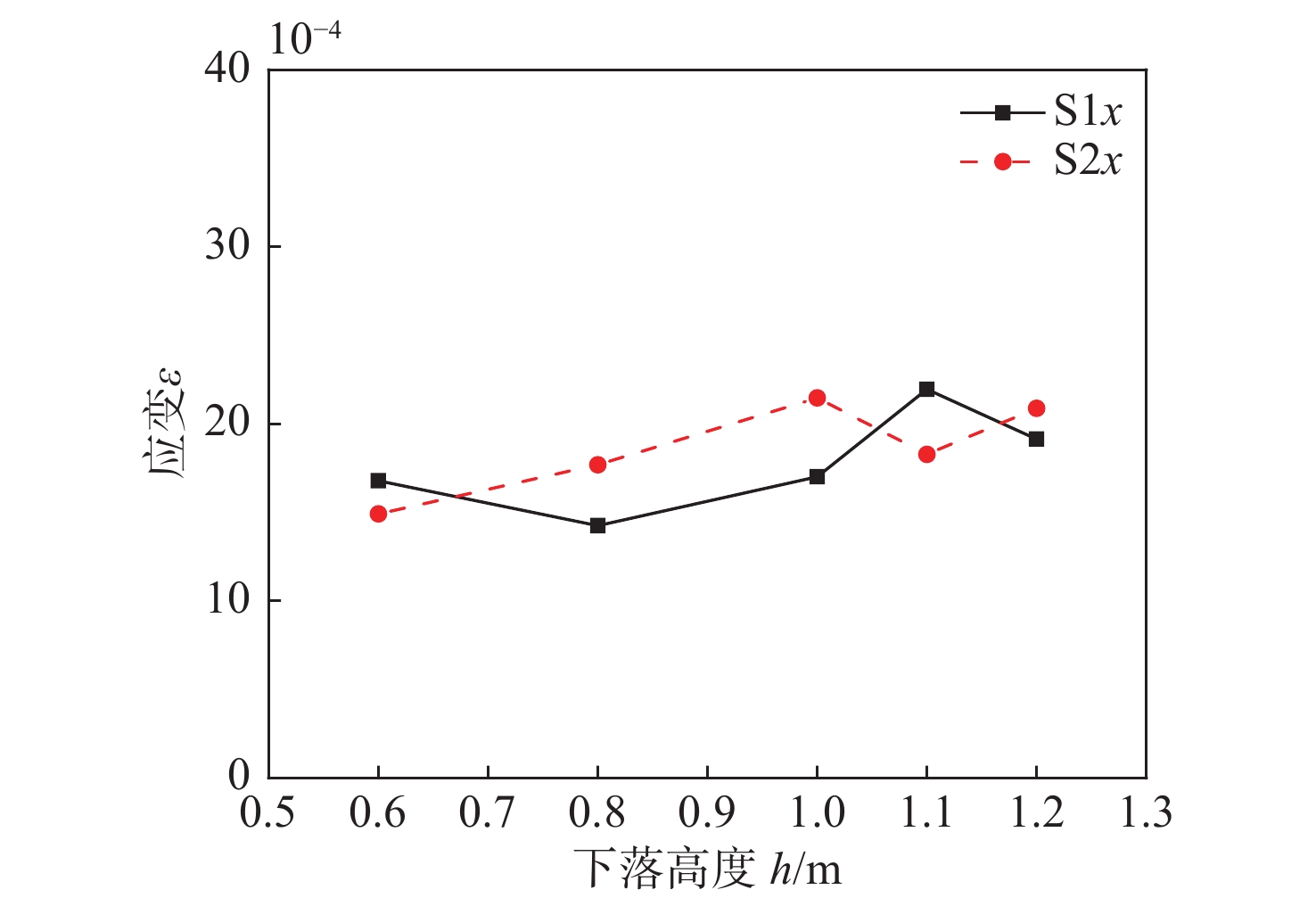
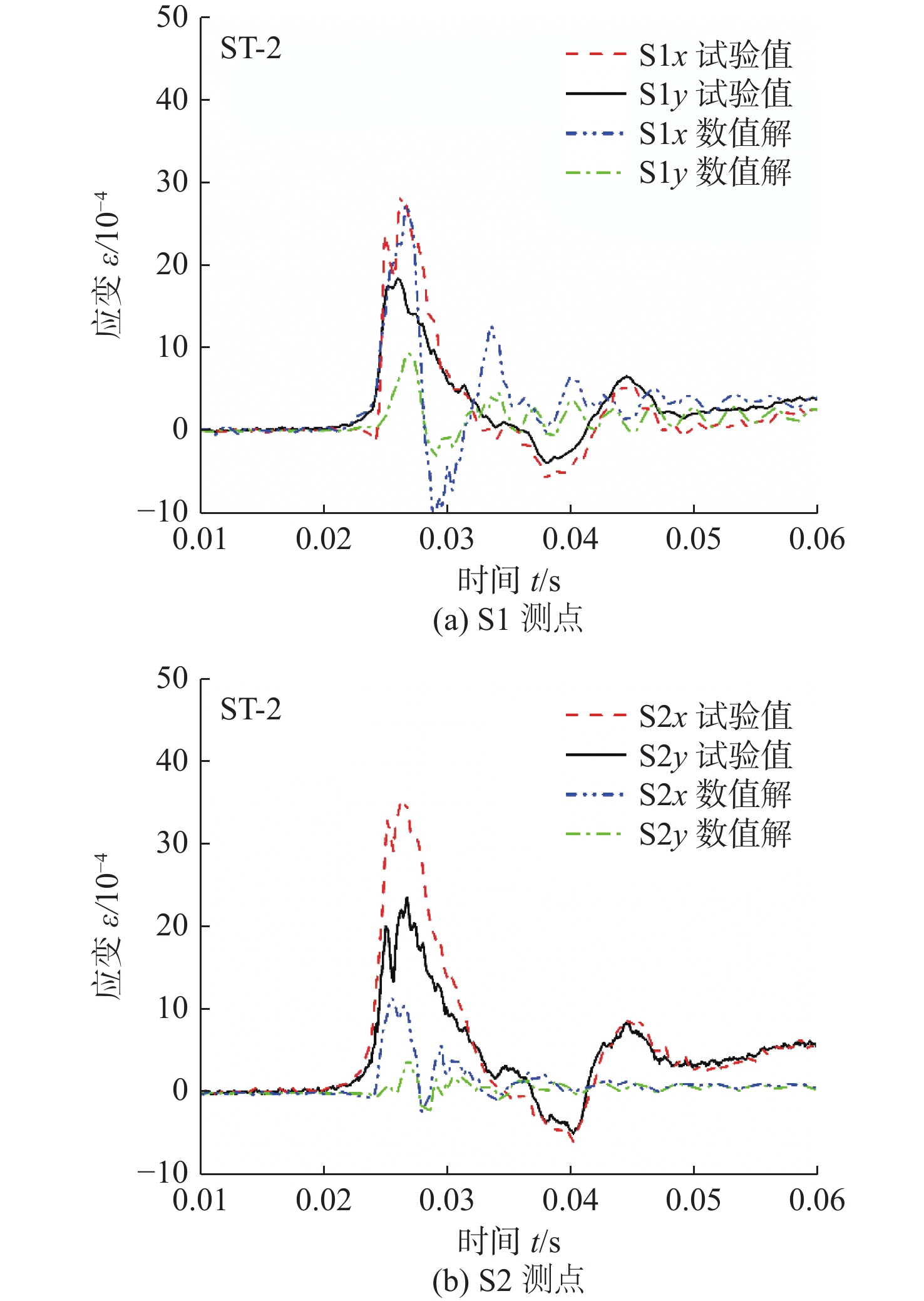
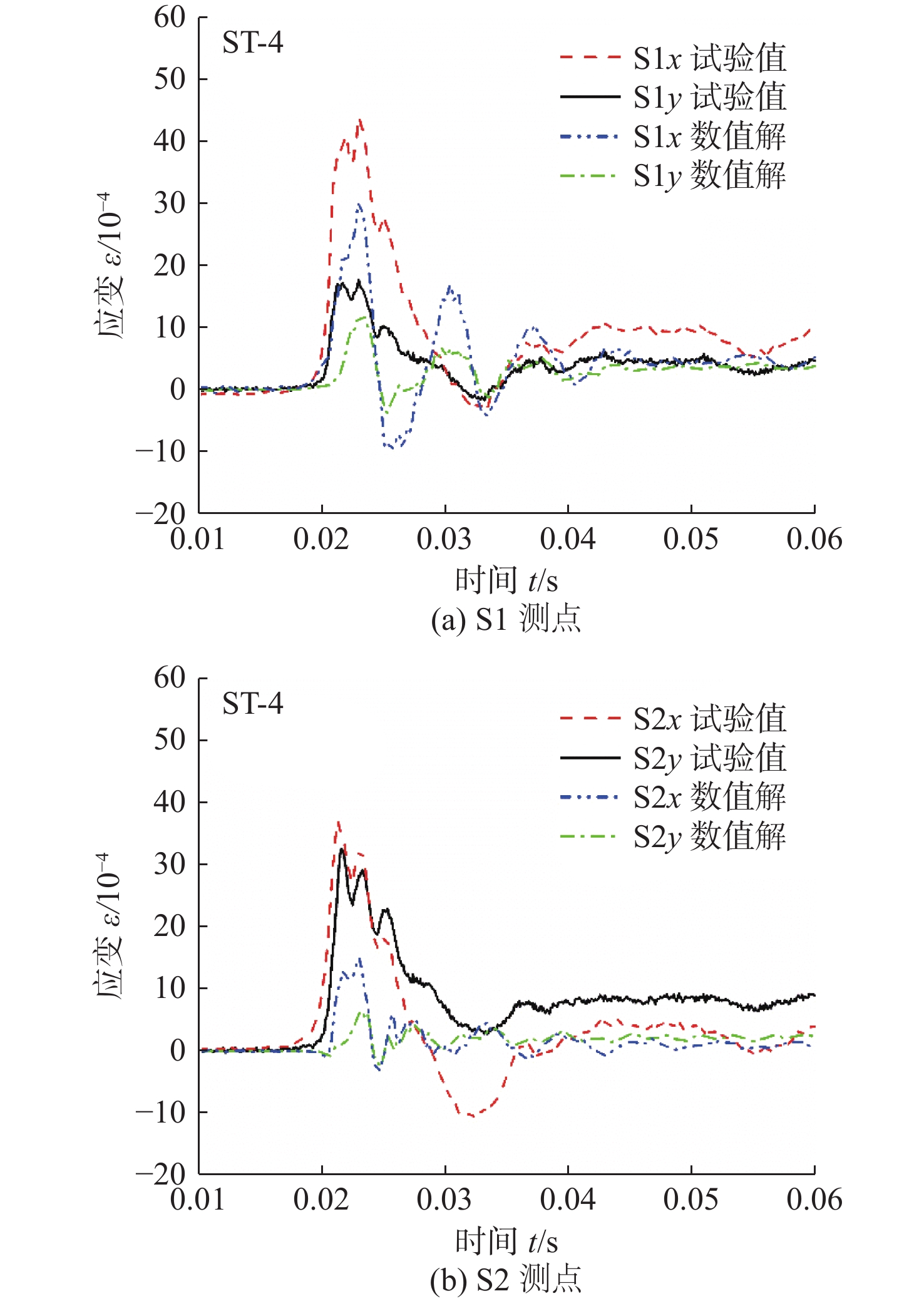
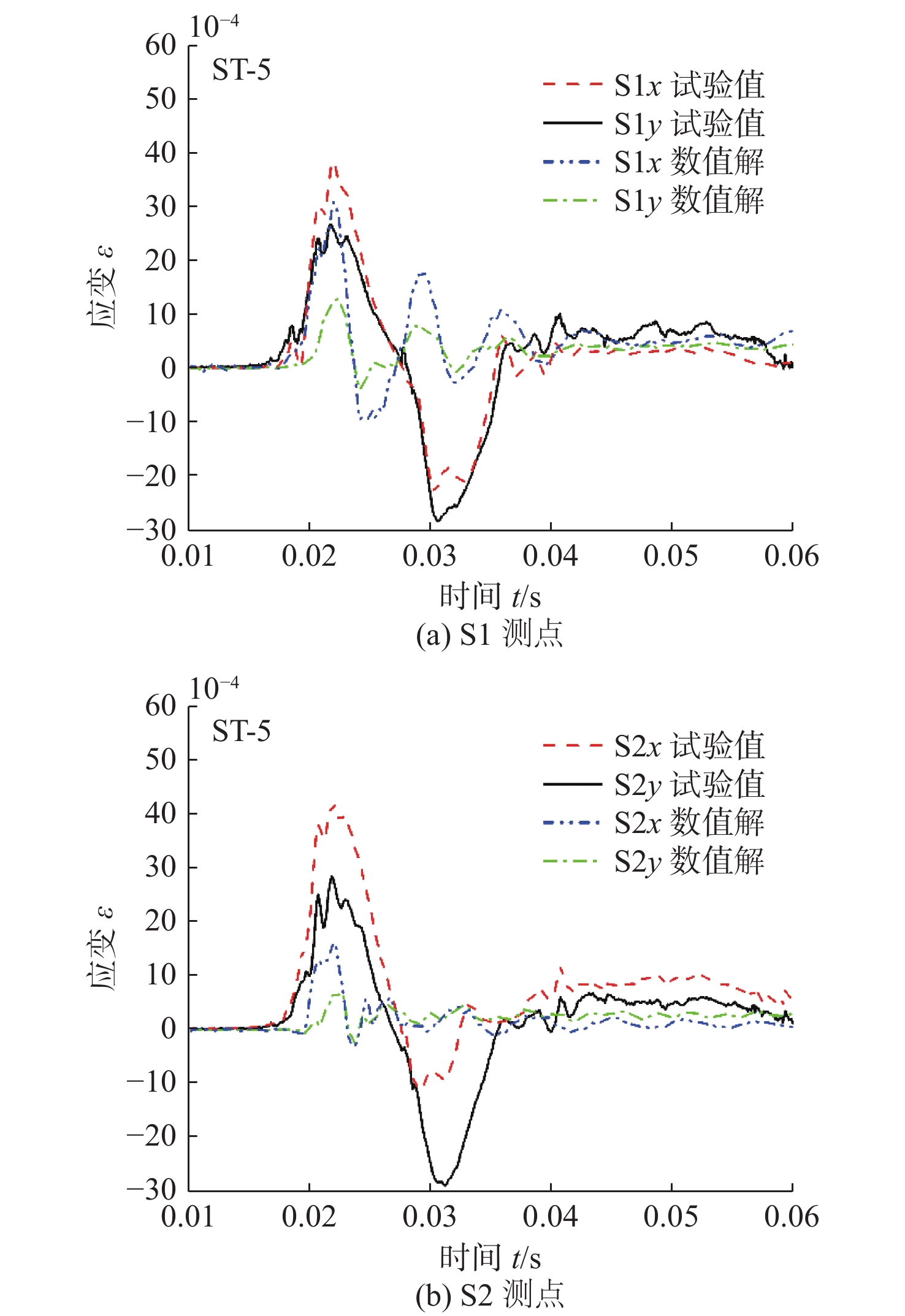
图 6 加筋平板中心压力测点在典型落体高度下的重复测量数据Figure 6. Repeated measurement data of pressure measuring point at the cetnter of reinforced flat plate for typical drop heights图7为不同高度下加筋平板试验模型各测点应变，图8为不同试验高度下S1x和S2x测点的应变峰值随落体高度的变化关系。初始时刻与冲击压力曲线相同，取试验模型下落至距水面0.1时刻。从图7中可以看出，应变上升时间与冲击压力上升时间基本相同，且随着下落高度的增加，应变峰值逐渐增大，应变曲线末期越快趋于平稳。其中，应变测点x向表示垂直加强筋方向，y向表示沿加强筋方向。可以看出，除1.1 m高度工况外，加强筋底部S2测点应变曲线在变化趋势和峰值大小均大于加筋平板中心S1测点测量应变值，这可能是因为在变形较小时S2测点处有较大的弯曲应变，而S1测点处的弯曲和中面应力都较小。图8中给出了S1x和S2x测点处的应变峰值随落体高度的变化关系。可以发现，总体上S1测点的应变结果较S2测点要小，但整体的应变峰值基本随着落体高度的增加而增大。
![]()
图 8 S1x和S2x测点的应变峰值随落体高度的变化关系Figure 8. Variation of peak strain with drop height for measuring points S1x and S2x.同时，对比图4压力曲线和图7应变时程曲线。可以发现，应变峰值往往出现在冲击压力峰值后期，即压力衰减阶段，这表明在冲击压力持续加载过程中，加筋平板变形达到某一特定值后不再增加，只有前一部分压力脉冲载荷对结构的最大变形起作用的，说明试验板在整个入水冲击过程中，横向变形会达到饱和，这在Zhu等[18]的船体单板砰击试验中发现了饱和冲量现象相呼应，本文在加筋板的砰击试验中也发现了饱和冲量现象。饱和冲量现象的研究表明，仅有饱和时间之前的脉冲对结构响应有影响，而其他的加载脉冲将不会对结构最大塑性变形做出贡献。因此，在结构设计压力等效过程中可对冲量进行适当折减。
3. 数值仿真模型
试验模型四周固定区域用低碳钢板压紧，因此在试验过程中认为该区域是刚性的，冲击只发生在围板以内的冲击区域，可以将模型简化为有效冲击区域的加筋平板和刚性支撑边界两部分。本节采用基于ALE耦合算法的ANSYS/LS-DYNA软件对所有的试验工况进行数值模拟。
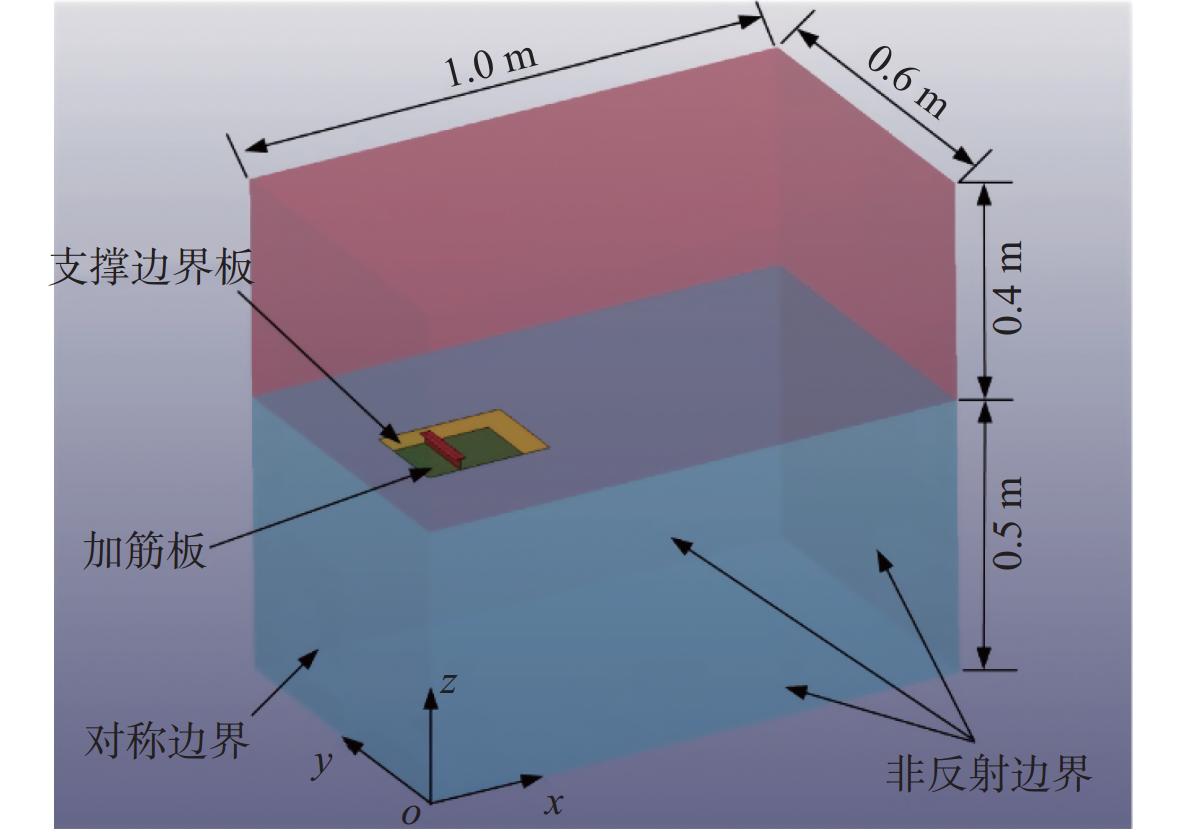
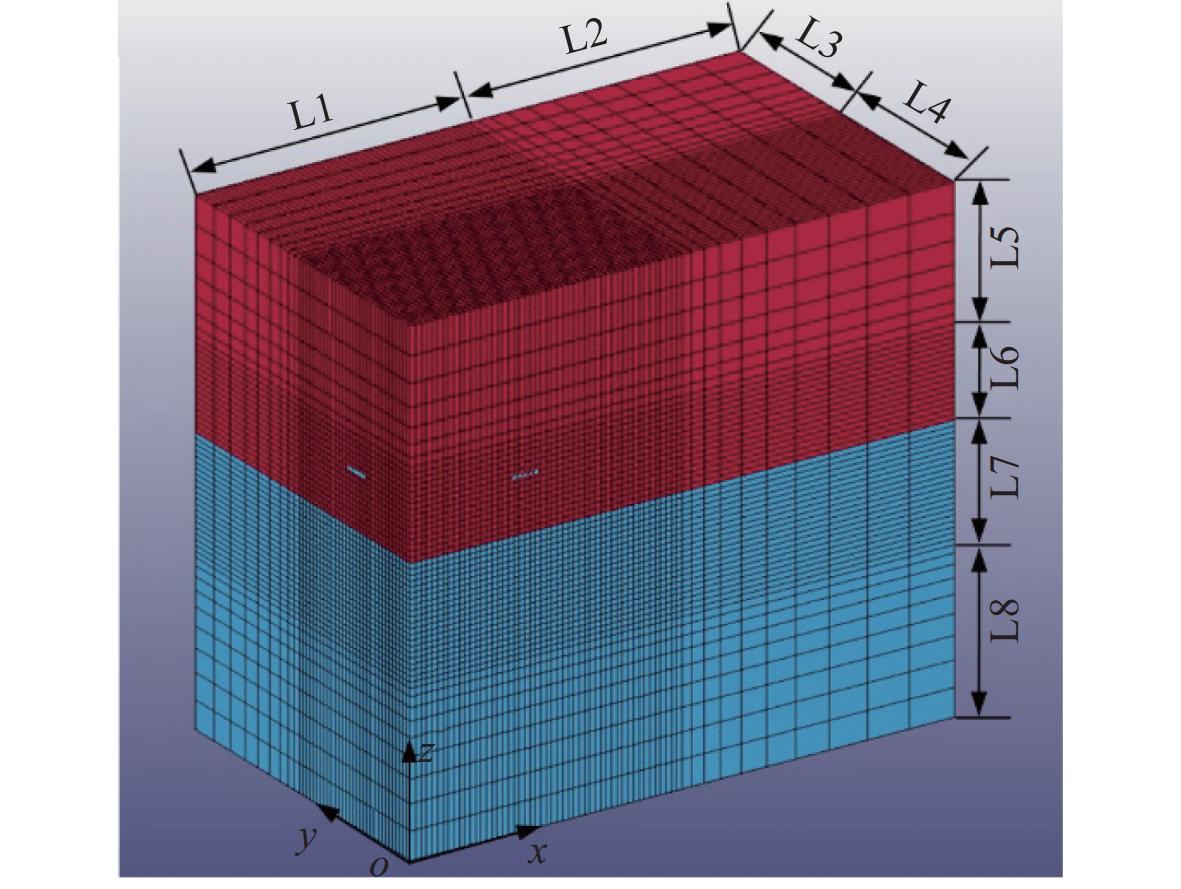
模型由流体（空气和水）和试验模型（加筋平板和刚性支撑边界）两部分组成。由于试验模型具有对称性，为了减少计算量，节约计算时间，取1/4试验模型进行计算分析，xoz平面和yoz平面在软件中被设置为对称边界。如图9所示，流体域尺寸大于模型尺寸3倍，满足ABS规范非反射边界条件要求，为避免边界波浪反射对数值计算结果的影响，除对称面xoz平面和yoz平面，其他边界均设置为非反射边界，以模拟无限水域。入水冲击区域（水和空气交界处）的流体的网格尺寸需要精细和均匀，对于远离冲击影响的区域，网格尺寸则沿着边界方向进行适度扩展，可以显著减少计算时间，流体区域网格划分形式如图10所示，具体尺寸参考表2。此外，根据已有的数值研究表明[24]，针对主要砰击区域，结构与流体的网格尺寸建议保持一致。因此，本文数值模型中的主要砰击区域内(L1×L4×(L6+L7))结构与流体的网格尺寸均设置为10 mm。
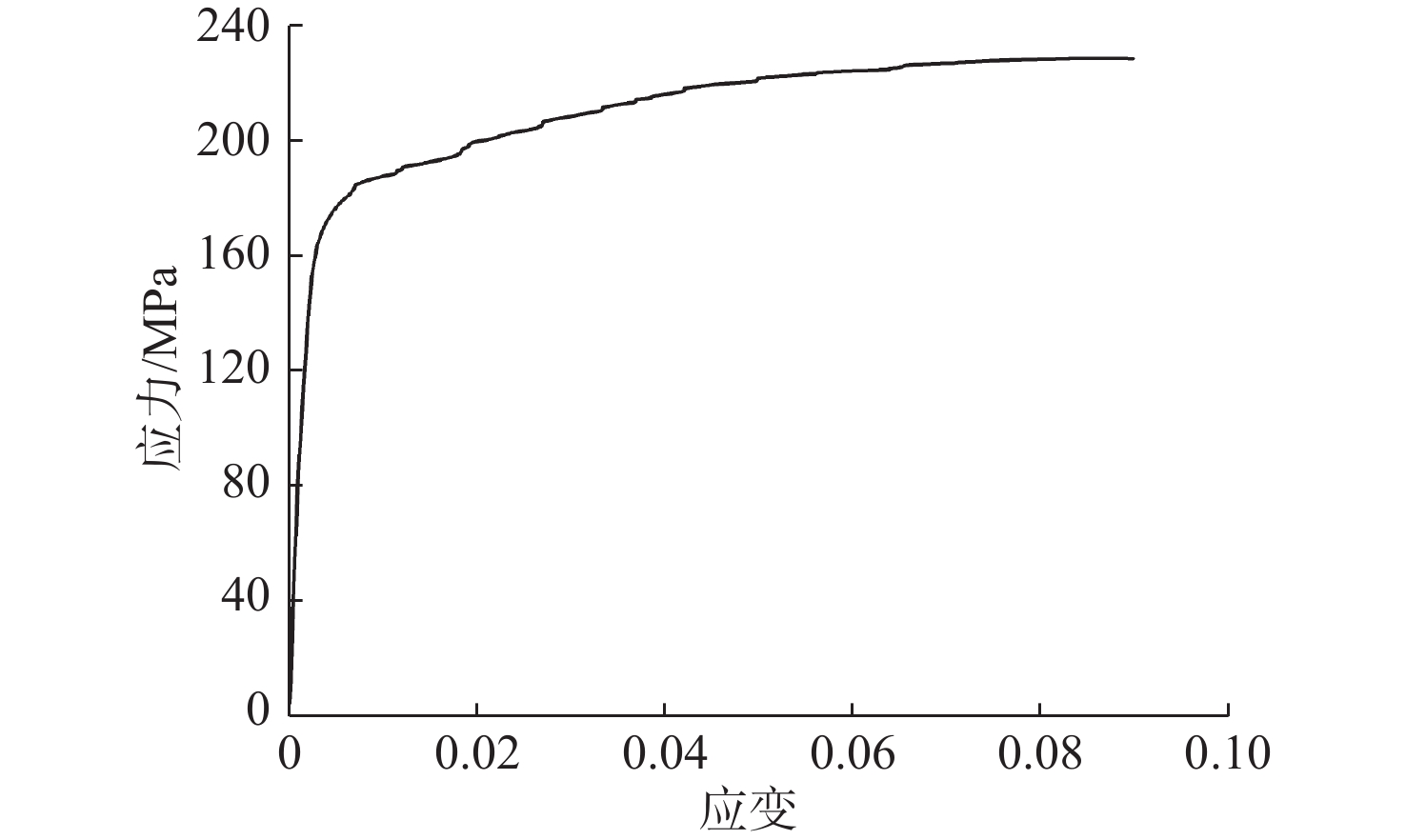
表 2 仿真模型流体区域尺寸Table 2. Simulation model fluid region size区域 L1 L2 L3 L4 L5 L6 L7 L8 尺寸/ m 0.5 0.5 0.3 0.3 0.25 0.15 0.2 0.3 数值模型中空气域和水域采用Solid164单元、材料模型为*009-MAT_NULL，这种材料属性不计算偏应力，也称为空属性材料，通常与状态方程配合使用，来模拟流体内部的压力。试验板和刚性支撑边界采用Shell163单元，其中加筋平板材料模型为*024-PIECEWISE_LINEAR_PLASTICITY，并输入铝合金拉伸试验测得的真实应力−应变曲线结果，如图11所示。为模拟实际试验中的刚性支撑边界，采用了*001-MAT-ELASTIC材料模型，保证数值模拟中边界处仅产生弹性响应。材料参数如下：杨氏模量210 GPa，屈服极限235 MPa，密度7 850 kg/m³，泊松比0.3。此外，支撑边界的边缘添加质量点单元Mass166，质量数值为1/4试验箱体和滑动平台质量，以便与试验模型质量对应。为节约计算时间，模型在水面上方0.1 m高度处释放，通过考虑结构的重力加速度，可以计算出试验模型自由下落至静水面时刻的冲击速度。
4. 数值结果分析
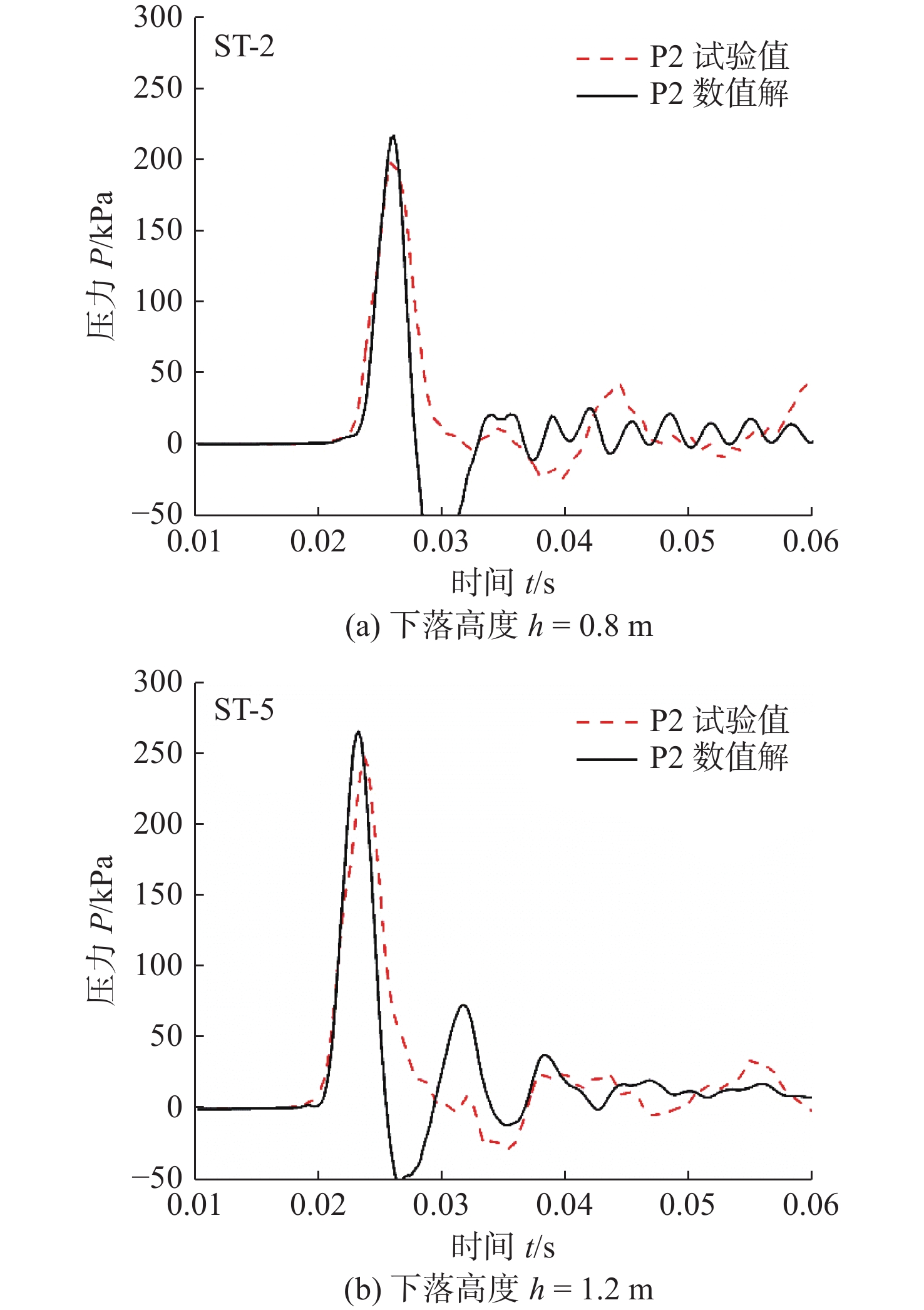
图4中压力曲线数据已经证明了平底结构入水冲击压力具有良好的均布特性，因此本节仅对试验模型中心测点（P2测点）压力进行分析讨论。图12为高度工况0.8 和1.2 m时加筋平板中心压力对比结果。从图中可以看出，仿真计算的冲击压力峰值比试验值略大，压力曲线末期数值振动稍大，但变化趋势十分吻合。数值计算压力峰值持续时间要略小于试验测量值，但载荷上升段持续时间十分接近。
![]()
图 12 加筋平板中心处冲击压力的试验值和数值解Figure 12. Testing values and numerical solutions of impact pressure at the center of a reinforced flat plate图13～图15为落体高度为0.8 ，1.1和1.2 m工况下不同位置应变时程曲线的试验值与数值解的对比情况。从图中可以看出，除了0.8 m工况S1应变测点外，其他高度工况各测点应变响应数值解均小于试验值，可能是因为数值模型是较为理想的，数值模型中结构的边界条件被简化为完全刚性固定。S1测点沿y方向的应变响应数值解与试验值在应变变化趋势和峰值大小上吻合度均较好，但数值解的衰减周期小于试验值。另外，在加工焊接过程中，高温会降低焊接部位的结构强度，也可能会对结果造成一定的影响。
![]()
图 13 结构应变的试验值和数值解（h=0.8 m）Figure 13. Testing values and numerical solutions of structural strains (h=0.8 m)![]()
图 14 结构应变的试验值和数值解（h=1.1 m）Figure 14. Testing values and numerical solutions of structural strains（h=1.1 m）![]()
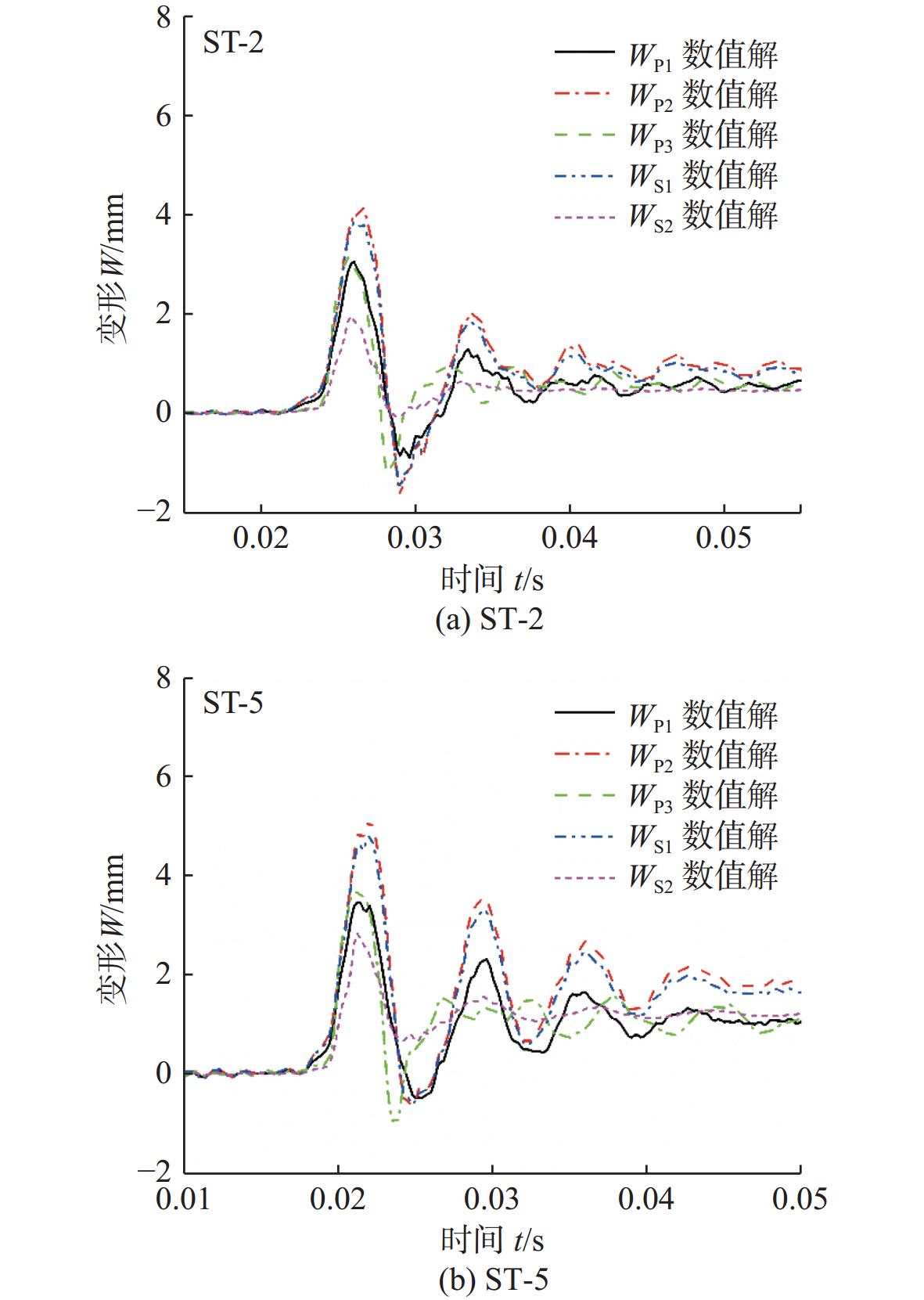
图 15 结构应变的试验值和数值解（h=1.2 m）Figure 15. Testing values and numerical solutions of structural strains (h=1.2 m)为研究不同位置结构变形情况，图16展示了试验模型入水冲击后不同测点位置变形情况的数值解。图例中，WP1表示加筋平板P1测点处横向变形值，其他依此类推。从图中可以看出，结构最大变形值出现在加筋平板中心位置，且越远离平板中心位置结构横向变形值越小，但加强筋底部S1测点位置变形小于P3测点位置变形值，这也与S2测点应变小于S1测点应变结果相关。
![]()
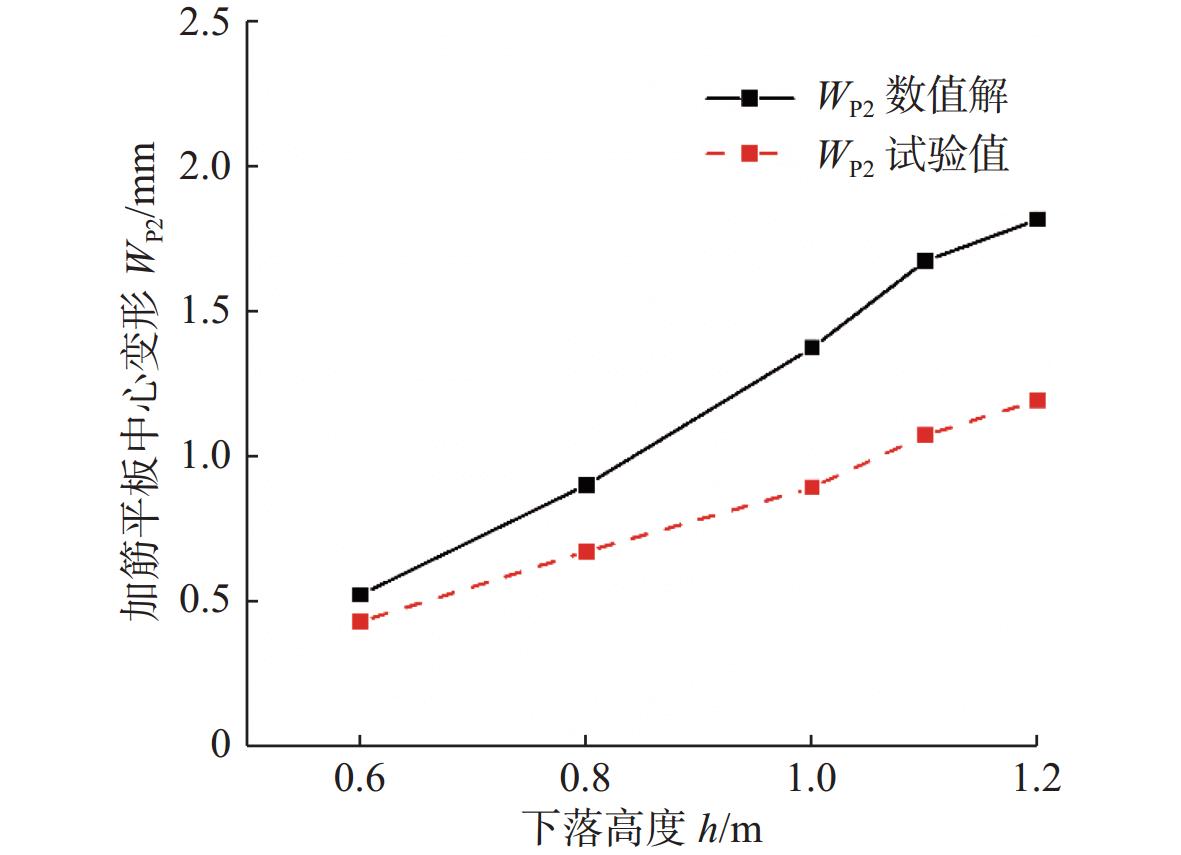
图 16 加筋平板不同位置变形值Figure 16. Deformation values of stiffened slab plate at different locations图17比较了通过3D扫描相机得到的试验加筋平板中心变形值与数值仿真计算WP2变形结果。其中试验值取3D扫描相机4次重复试验测量变形的均值，数值仿真变形取曲线衰减直平稳后第一个波峰与波谷的均值。平板中心变形的数值解和试验测量值在变化趋势上比较吻合，但随着落体高度的增加，变形值差距逐渐增大。这是因为与结构响应一样，相同的落体高度、相同的入水角度条件下，试验测量的变形值也有一定的差异，这与冲击的离散型有直接关系。
![]()
图 17 不同落体高度下加筋平板中心变形值Figure 17. Central deformation values of stiffened slab plate under different drop heights5. 结 论
针对铝制高速舰艇冲击问题，本文设计了一组铝合金加筋平板模型，开展了不同高度的平底结构落体冲击实验，并于数值模拟结果进行对比，对试验模型入水过程中的冲击压力、结构响应以及最终变形进行了研究分析，所得结论对铝制船舶冲击结构设计及理论推导具有一定参考意义。本文研究结果总结如下：
1） 试验和仿真结果表明，平底结构入水冲击过程中，各测点冲击压力峰值发生时刻几乎相同，冲击压力具有均布特性，在计算平底结构冲击载荷作用下船体结构响应可将冲击载荷简化为均布脉冲载荷。
2） 加强筋对其周围结构刚度有着促进作用，随着刚度的增加，结构应力响应和变形在靠近加强筋的位置显著降低，但冲击压力峰值无较大改变，说明结构刚度对冲击压力峰值的影响远小于对结构响应的影响，且最大残余变形出现在加筋板中心位置。
3） 冲击发生后，结构应变峰值和最大变形值往往出现在冲击压力峰值后某一时刻，即压力衰减阶段，这表明加筋板结构在砰击压力持续加载过程中也存在“饱和冲量”现象。因此，加筋板入水砰击过程中仅有饱和时间之前的压力脉冲对结构的最大变形做出贡献，在结构设计压力等效过程中应考虑结构的饱和冲量现象。
-
![]()
图 2 试验加筋平板模型尺寸及测点布置
Figure 2. Sizes and measuring points arrangement of testing reinforced flat plate model
![]()
图 4 铝合金加筋平板冲击压力分布
Figure 4. Impact pressure distribution of aluminum alloy stiffened plate
![]()
图 5 不同测点处的砰击压力峰值以及P1测点处的压力冲量随落体高度的变化关系
Figure 5. Variation of peak slamming pressure at different measuring points and impulse at P1 mearuring point with drop heights of falling body
![]()
图 6 加筋平板中心压力测点在典型落体高度下的重复测量数据
Figure 6. Repeated measurement data of pressure measuring point at the cetnter of reinforced flat plate for typical drop heights
![]()
图 8 S1x和S2x测点的应变峰值随落体高度的变化关系
Figure 8. Variation of peak strain with drop height for measuring points S1x and S2x.
![]()
图 12 加筋平板中心处冲击压力的试验值和数值解
Figure 12. Testing values and numerical solutions of impact pressure at the center of a reinforced flat plate
![]()
图 13 结构应变的试验值和数值解（h=0.8 m）
Figure 13. Testing values and numerical solutions of structural strains (h=0.8 m)
![]()
图 14 结构应变的试验值和数值解（h=1.1 m）
Figure 14. Testing values and numerical solutions of structural strains（h=1.1 m）
![]()
图 15 结构应变的试验值和数值解（h=1.2 m）
Figure 15. Testing values and numerical solutions of structural strains (h=1.2 m)
![]()
图 16 加筋平板不同位置变形值
Figure 16. Deformation values of stiffened slab plate at different locations
![]()
图 17 不同落体高度下加筋平板中心变形值
Figure 17. Central deformation values of stiffened slab plate under different drop heights
表 1 试验工况表
Table 1 Test condition
工况
序号下落
高度/m理论入水
速度/(m·s−1)实测入水
速度/(m·s−1)试验
次数ST-1 0.6 3.43 3.36 4 ST-2 0.8 3.96 3.89 1 ST-3 1.0 4.43 4.31 1 ST-4 1.1 4.65 4.54 1 ST-5 1.2 4.85 4.75 4 
下载: 导出CSV
表 2 仿真模型流体区域尺寸
Table 2 Simulation model fluid region size
区域 L1 L2 L3 L4 L5 L6 L7 L8 尺寸/ m 0.5 0.5 0.3 0.3 0.25 0.15 0.2 0.3
下载: 导出CSV
-
[1] WANG S, GUEDES SOARES C. Review of ship slamming loads and responses[J]. Journal of Marine Science and Application, 2017, 16(4): 427–445. doi: 10.1007/s11804-017-1437-3
[2] CHUANG S L. Experiments on flat-bottom slamming[J]. Journal of Ship Research, 1966, 10(1): 10–17. doi: 10.5957/jsr.1966.10.1.10
[3] CHUANG S L. Investigation of impact of rigid and elastic bodies with water: No. 3248[R]. Washington D.C: Department of the Navy; 1970.
[4] ZHU L, FAULKNER D. Design pressure for the wet-deck structure of twin-hull ships[C]//Proceedings of the 3rd International Conference on Fast Sea Transportation. Germany: Schiffbautechnische Gesellschaft, 1995.
[5] WANG S, GUEDES SOARES C. Experimental and numerical study of the slamming load on the bow of a chemical tanker in irregular waves[J]. Ocean Engineering, 2016, 111: 369–383. doi: 10.1016/j.oceaneng.2015.11.012
[6] 于鹏垚, 王天霖, 任慧龙, 等. 船首外飘砰击设计载荷影响因素研究[J]. 中国造船, 2019, 60(1): 60–68. YU P Y, WANG T L, REN H L, et al. Research on influence factors of bow-flared slamming loads under design condition[J]. Shipbuilding of China, 2019, 60(1): 60–68 (in Chinese).
[7] 姜宜辰, 孙振东, 宗智, 等. 气垫效应对三体船连接桥砰击载荷的影响[J]. 中国舰船研究, 2021, 16(5): 197–205. doi: 10.19693/j.issn.1673-3185.01919 JIANG Y C, SUN Z D, ZONG Z, et al. Effects of air cushion on slamming load of trimaran cross-deck structure[J]. Chinese Journal of Ship Research, 2021, 16(5): 197–205 (in Chinese). doi: 10.19693/j.issn.1673-3185.01919
[8] DUAN L L, ZHU L, CHEN M S, et al. Experimental study on the propagation characteristics of the slamming pressures[J]. Ocean Engineering, 2020, 217: 107868. doi: 10.1016/j.oceaneng.2020.107868
[9] JONES N. Slamming damage[J]. Journal of Ship Research, 1973, 17(2): 80–86. doi: 10.5957/jsr.1973.17.2.80
[10] FALTINSEN O M, KVÅLSVOLD J, AARSNES J V. Wave impact on a horizontal elastic plate[J]. Journal of Marine Science and Technology, 1997, 2(2): 87–100. doi: 10.1007/BF02491523
[11] FALTINSEN O M. The effect of hydroelasticity on ship slamming[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1997, 355(1724): 575–591. doi: 10.1098/rsta.1997.0026
[12] WANG S, GUEDES SOARES C. Hydroelastic analysis of a rectangular plate subjected to slamming loads[J]. Journal of Marine Science and Application, 2017, 16(4): 405–416. doi: 10.1007/s11804-017-1434-6
[13] 任慧龙, 翟帅帅, 于鹏垚, 等. 砰击载荷作用下船艏结构瞬态响应研究[J]. 中国舰船研究, 2013, 8(6): 14–19. doi: 10.3969/j.issn.1673-3185.2013.06.003 REN H L, ZHAI S S, YU P Y, et al. Transient response of the bow structure under slamming loads[J]. Chinese Journal of Ship Research, 2013, 8(6): 14–19 (in Chinese). doi: 10.3969/j.issn.1673-3185.2013.06.003
[14] ZHU L, DUAN L L, CHEN M S, et al. Equivalent design pressure for ship plates subjected to moving slamming impact loads[J]. Marine Structures, 2020, 71: 102741. doi: 10.1016/j.marstruc.2020.102741
[15] 田阿利, 姚鹏, 傅梓轩, 等. SPS覆层船艏局部加强结构的抗砰击性能仿真分析[J]. 中国舰船研究, 2020, 15(4): 59–65. doi: 10.19693/j.issn.1673-3185.01631 TIAN A L, YAO P, FU Z X, et al. Simulation analysis on slamming mechanical properties of SPS-clad partially strengthened bow[J]. Chinese Journal of Ship Research, 2020, 15(4): 59–65 (in Chinese). doi: 10.19693/j.issn.1673-3185.01631
[16] MORI K. Response of the bottom plate of high speed crafts under impulsive water pressure[J]. Journal of the Society of Naval Architects of Japan, 1977, 1977(142): 297–305.
[17] 骆寒冰, 刘鑫, 董德龙, 等. 铝制加筋板楔形体入水砰击模型实验研究[J]. 水动力学研究与进展, 2014, 29(4): 460–468. LUO H B, LIU X, DONG D L, et al. Experimental investigation of water impact of one free-drop wedge with stiffened aluminum panels[J]. Chinese Journal of Hydrodynamics, 2014, 29(4): 460–468 (in Chinese).
[18] ZHU L, ZHU Z K, YU T X, et al. An experimental study of the saturated impulse for metal plates under slamming[J]. International Journal of Impact Engineering, 2023, 178: 104601. doi: 10.1016/j.ijimpeng.2023.104601
[19] ZHAO Y P, YU T X, FANG J. Large dynamic plastic deflection of a simply supported beam subjected to rectangular pressure pulse[J]. Archive of Applied Mechanics, 1994, 64(3): 223–232. doi: 10.1007/BF00806819
[20] ZHU L, BAI X Y, YU T X. The saturated impulse of fully clamped square plates subjected to linearly decaying pressure pulse[J]. International Journal of Impact Engineering, 2017, 110: 198–207. doi: 10.1016/j.ijimpeng.2016.12.012
[21] BAI X Y, ZHU L, YU T X. Saturated impulse for fully clamped square plates under blast loading[J]. International Journal of Mechanical Sciences, 2018, 146-147: 417–431. doi: 10.1016/j.ijmecsci.2017.08.047
[22] 赵飞, 程远胜, 刘均, 等. 入水砰击下金字塔点阵夹层板塑性动力响应分析[J]. 船海工程, 2013, 42(3): 13–16. ZHAO F, CHENG Y S, LIU J, et al. Dynamic plastic responses of light weight pyramidal sandwich plate structures subjected to water-entry impact[J]. Ship & Ocean Engineering, 2013, 42(3): 13–16 (in Chinese).
[23] LIU D, ZHU L, GUO K L, et al. Dynamic responses of aluminum honeycomb sandwich plate under slamming loadings[C]//Proceedings of the 32nd International Ocean and Polar Engineering Conference. Shanghai, China: [s. n. ], 2022.
[24] TRUONG D D, JANG B S, JU H B, et al. Prediction of slamming pressure considering fluid-structure interaction. Part I: numerical simulations[J]. Ships and Offshore Structures, 2022, 17(1): 7–28. doi: 10.1080/17445302.2020.1816732
计量
- 文章访问数: 146
- HTML全文浏览量: 21
- PDF下载量: 30
