Research on dynamic performance and heave suppression of FDPSO vessel based on model tests: a comprehensive analysis of influence of heave plate arrangements
-
摘要:目的
研究新型深水八角浮式钻井生产储卸油轮（FDPSO）在不同垂荡板布置下的动力性能，为我国南海 FDPSO 设计提供指导。
方法采用1:60 缩尺比制作模型，设置单层垂荡板、不同间距双层垂荡板，开展自由衰减测试、白噪声测试、一年一遇和百年一遇风浪流联合作用测试，测量 FDPSO 重心处六自由度运动、系泊系统载荷、典型位置加速度等。
结果结果表明，单层垂荡板浮体运动固有周期最小，垂荡无因次阻尼比最大；双层垂荡板综合考虑增阻效果和垂荡板出水问题，最佳无量纲间距选定为λ = 0.5；λ = 0.5的双层垂荡板的幅频响应算子（RAO）峰值大于单层垂荡板；百年一遇海况下双层垂荡板有出水和上浪现象，单层垂荡板运动抑制效果更好，浮体运动、系缆力、典型位置加速度均小于双层垂荡板；一年一遇海况不同垂荡板设置锚链力相差不大，百年一遇海况下单层垂荡板锚链力明显小于双层垂荡板。
结论综合各项测试，单层垂荡板在运动抑制方面表现更优，实际设计可考虑采用单层垂荡板布置形式，但双层垂荡板间距确定还需更详细的试验分析。
Abstract:ObjectiveThis paper studies the dynamic performance of a new deep-water octagonal floating drilling production storage and offloading (FDPSO) unit under different heave plate arrangements to provide guidance for the design of an FDPSO in the South China Sea.
MethodModels are made with a scale ratio of 1:60. Single-layer and double-layer heave plates with different spacings are set up. Free decay tests, white noise tests, and combined wind-wave-current tests for one-year and one-hundred-year return periods are carried out. The six-degree-of-freedom motion at the center of gravity of the FDPSO, mooring system loads, acceleration at typical positions, etc. are measured.
ResultsThe results show that the single-layer heave plate has the smallest natural period of floating body motion and the largest dimensionless damping ratio for heave. Considering the drag-increasing effect and the problem of heave plate emergence, the optimal non-dimensional spacing for the double-layer heave plate is selected as λ = 0.5. The peak response amplitude operator (RAO) of the double-layer heave plate with λ = 0.5 is greater than that of the single-layer heave plate. Under the one-hundred-year return period sea state, the double-layer heave plate shows emergence and wave climbing phenomena, while the single-layer heave plate has a better motion suppression effect with smaller floating body motion, mooring force, and acceleration at typical positions than those of the double-layer heave plate. In the one-year return period sea state, the difference in anchor chain forces for different heave plate arrangements is not significant, and in the one-hundred-year return period sea state, the anchor chain force of the single-layer heave plate is significantly smaller than that of the double-layer heave plate.
ConclusionBased on various tests, the single-layer heave plate has better motion suppression performance. In actual design, the single-layer heave plate arrangement can be considered, but a more detailed experimental analysis is required to determine the spacing of the double-layer heave plate.
-
0. 引 言
浮式钻井生产储卸油轮（FDPSO）是具备油矿钻探、原油生产、储备以及外输等多种功能的海洋工程船舶，其在浮式生产储卸油装置（FPSO）基础上增加钻井功能，能在钻井的同时进行生产，具有较好的应用前景[1]。目前，世界上已经建成的FDPSO总共有3艘：大连中远船务建造的船型FDPSO(MPF-
1000 )，是世界首艘浮式钻井生产储油平台，2008年12月完工；新加坡吉宝船厂建造的船型FDPSO（Azurite），2009年8月在刚果共和国海域的 Azurite 油田正式投产，由一艘超大型油轮（VLCC）改造而成；南通中远船务建造的Sevan Driller，是世界首座圆筒形FDPSO，2009年6月建成。FDPSO因排水量大、所处环境条件恶劣，其运动稳定性至关重要，增加垂荡板可以有效减小浮体的垂荡运动[2]，国内外学者对FPDSO及其垂荡板的水动力、运动等性能进行了研究。刘利琴等[3]在Sevan型FPSO基础上改变垂荡板结构，对不同海况下垂荡板倾角变化和阻尼特性减摇效果进行研究，结果表明小锥角垂荡板对浮体的垂荡运动的抑制效果好。黄孟丽等[4]对高海况条件下的新型圆通FDPSO垂荡运动进行数值模拟计算，主要研究不同减动结构宽度高度对浮体垂荡运动的影响。姚宇鑫等[5]在对各类深水浮式平台进行深入分析和总结的基础上提出沙漏型浮式结构的概念，并初步对此新型FDPSO的外形进行设计优化。晏柳等[6]探究锚链预张力与FDPSO运动相应之间的关系，发现浮体纵荡、横荡和横摇的运动受锚链预张力的影响比较显著。Philip等[7]研究了圆形垂荡板对单柱式（SPAR）储油平台动力性能的影响，对无垂荡板、一个垂荡板、两个垂荡板等情况进行模型实验与数值模拟，研究表明垂荡板可以明显增大结构阻尼系数及附加质量参数，而双层垂荡板比单层效果更加显著，运动响应最小。Concalves等[8]研究带有圆形月池的圆通型浮体，得出浮体的垂荡固有周期受垂荡板的影响较大。Li等[9]在FDPSO平台的基础上，增加一个扩张圆柱体及其新的阻尼结构，提出一种圆柱形FDPSO平台。针对两种特殊的系泊系统，结合南海环境，采用时域耦合分析方法，对平台−系泊系统的动力学性能进行数值模拟。结果表明，采用“链−聚酯−链”式系泊系统能满足平台运动响应和规范要求。Romain等[10]采用CFD数值模型研究垂荡阻尼板在受迫垂向运动中的流固耦合过程，其CFD结果很好地预测了大的振荡周期和升沉运动的各种幅度等。Shen等[11]对浮体垂荡运动受垂荡板不同外边缘形式的影响进行研究，结果表明，在一定范围内垂荡板的边缘越薄，其垂荡运动性能越好。Naciri等[12]研究多点系泊FPSO的水动力性能，再结合模型实验和数值分析对浮体的作业情况进行了预报。
针对南海海域，中海油研究总院提出八角形FDPSO设计方案。王世圣等[13]研究垂荡板对八角形FDPSO垂荡抑制性能，证明双层垂荡板的抑制效果优于单层垂荡板。于晨芳等[14]研究不同垂荡板数量、吃水深度、垂荡板宽度和垂荡板间距对深水八角形FDPSO垂荡运动的影响，结果表明，垂荡板的增设可以有效提升浮体的运动性能，增加垂荡板尺寸可以增大浮体垂荡固有周期，增加板距可以优化浮体垂荡运动性能。但是，以上工作均基于数值模拟展开，缺乏全面的试验验证。因此，本文将针对中海油研究总院设计的深水八角形FDPSO，基于模型试验来研究其动力性能，分析垂荡板设置对浮体垂荡运动的抑制效果，为我国南海FDPSO的设计提供指导。
1. FDPSO参数及试验过程
1.1 试验准则和测试设备
模型试验在上海交通大学海洋深水试验池开展。海洋深水试验池由水池主体和一个深井组成，可以模拟风、浪、流等各种海洋环境。水池的主体有效尺寸为50 m长、40 m宽，最大的工作水深为10 m。水深可在0～10 m范围内任意调节。水池深井最大工作水深40 m、直径5 m。主要设备有：造波系统、消波系统、造流系统、造风系统、水深调节系统、深井假底、拖车系统、数据采集系统，以及各种用以测量风、浪、流、力及海洋工程结构物模型运动的仪器设备。
模型试验保持实体与模型之间的傅汝德数和斯托哈尔数相等，即满足两者的重力相似和惯性相似，因此：
Vm√gLm=Vs√gLs (1) VmTmLm=VsTsLs (2) 式中V，L，T分别为速度、特征线尺度及主要周期，下标m及s分别表示模型和实体。根据上述相似法则，模型与实际平台主要物理量之间的转换关系见参考文献[15]。
1.2 FDPSO模型及参数
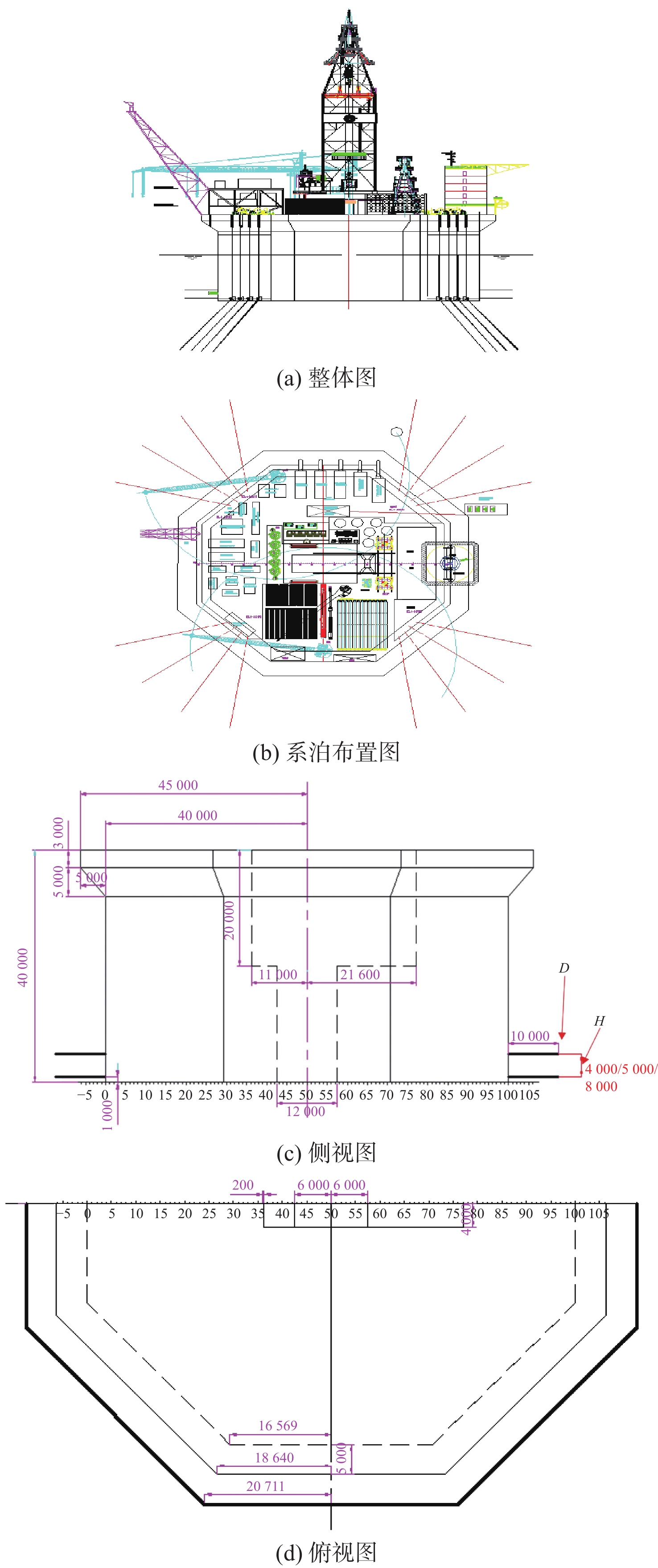
试验按照1:60缩尺比制作模型，针对满载工况进行测试分析。FDPSO船体主要尺度参数及模型参数如表1所示。船体型线如图1所示。总布置如图2（a）所示，系泊系统布置如图2（b）所示。垂荡板间距采用无因次参数λ表示，λ= H / D，其中D=10 m表示垂荡板圆环宽度，H为双层垂荡板的间距，具体如图2（b）所示。
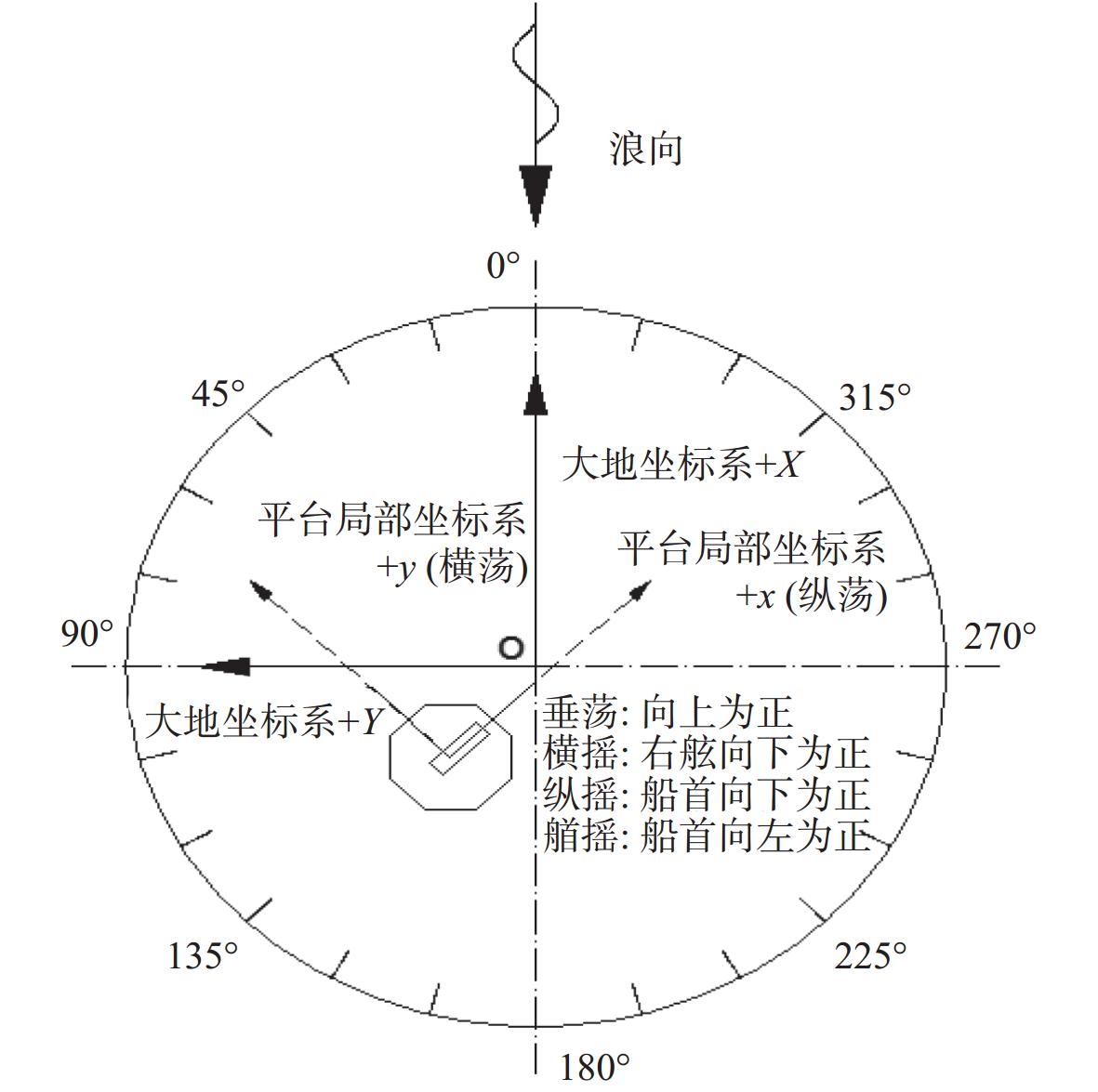
表 1 FDPSO船体主尺度参数Table 1. The main scale parameters of the FDPSO hull设计参数 符号 实体 模型 总长/m Loa 100 1.667 型宽/m B 100 1.667 型深/m D 40 0.667 吃水/m d 21.4 0.357 排水量/t Δ 107 520 0.544 重心纵向位置/m XG −0.17 −0.003 重心横向位置/m YG 0.37 0.006 重心垂向位置/m KG 24.07 0.401 横摇回转半径/m Rxx 29.52 0.492 纵摇回转半径/m Ryy 29.57 0.493 艏摇回转半径/m Rzz 35.05 0.584 模型试验中应用的大地坐标系O−XYZ和随体坐标系G−xyz，以及六自由度运动的方向定义，如图3所示。随体坐标系的原点在平台重心处。
1.3 试验工况及测试物理量
1） 自由衰减测试。
考虑不同的垂荡板间距和个数，针对满载工况开展FDPSO静水衰减试验，测试浮体垂荡、横摇、纵摇衰减曲线，测量获得FDPSO船体以及船体和锚泊系统耦合的固有运动周期和线性阻尼系数等，从而获得系统的固有属性。通过对不同垂荡板间距下试验结果的比较分析，确定最佳垂荡板间距值，具体的试验工况如表2所示。
表 2 自由衰减测试工况Table 2. Free decay test conditions试验序号 垂荡板间距λ 系泊方式 试验内容 15～17 0.4 / 横摇、纵摇、垂荡衰减 18～20 0.5 / 横摇、纵摇、垂荡衰减 21～23 0.8 / 横摇、纵摇、垂荡衰减 24～26 单层垂荡板 / 横摇、纵摇、垂荡衰减 27～28 0.5 4×4 纵荡、横荡衰减 2） 白噪声测试。
白噪声试验的目的是测量FDPSO船体在波浪作用下的幅频响应算子（RAO），从而获得FDPSO船体的水动力性能。在试验时通过水平系泊的方式将FDPSO船体在水池中定位，水平系泊模型参数为长40 m、刚度48 cm/kg、预张力1 kg。白噪声试验包括180°和150°两个角度，在单层垂荡板及双层垂荡板最佳间距下分别开展试验，工况如表3所示。
表 3 FDPSO系统RAO试验工况Table 3. FDPSO system RAO test conditions试验序号 垂荡板设置 角度/(°) 113 最佳垂荡板间距 180 114 最佳垂荡板间距 150 115 单层垂荡板 180 116 单层垂荡板 150 3） 风浪流联合作用测试。
风、浪、流试验的目的主要是全面测试在我国南海海域的环境条件下，该FDPSO生存和作业状态下的水动力性能，包括FDPSO船体的运动性能、加速度性能、系泊系统载荷等关键参数，为FDPSO方案设计和理论计算提供参考依据。仪器采样频率为20 Hz，风、浪、流试验的采样时间大于24 min，对应实际时间3 h，采样点数大于28 800点。风、浪、流试验包括风、浪、流同向和不同向，不规则波浪采用 JONSWAP 谱，考虑了一年一遇作业海况和百年一遇生存海况，双层垂荡板最佳间距和单层垂荡板等，工况表如表4所示，环境参数如表5所示。
表 4 风、浪、流试验工况Table 4. Wind, wave and current test conditions序号 模拟海况 垂荡板 风浪流角度 117 一年一遇 双层，最佳间距 风、浪、流同向180° 118 一年一遇 双层，最佳间距 风、浪135°，流180° 119 一年一遇 双层，最佳间距 风、浪、流同向150° 120 百年一遇 双层，最佳间距 风、浪、流同向180° 121 百年一遇 双层，最佳间距 风、浪135°，流180° 122 百年一遇 双层，最佳间距 风、浪、流同向150° 123 一年一遇 单层 风、浪、流同向150° 124 百年一遇 单层 风、浪、流同向150° 表 5 环境参数Table 5. Environmental parameters海况 有义波高/m 谱峰周期/s 风速/(m·s−1) 流速(m·s−1) 一年一遇 6.2 11.1 19.3 1.05 百年一遇 15 18 49.5 1.95 4） 测试物理量。
试验中主要对FDPSO重心处的六自由度运动、系泊系统载荷、典型位置的运动加速度等进行测试（均为惯性坐标系的结果），如表6所示。测试之前对试验环境条件和测试仪器进行充分的标定，确保测试结果正确。
表 6 多点系泊FDPSO波浪试验中测量的物理量Table 6. Physical quantities measured in multi-point moored FDPSO wave tests测试量 单位 通道说明 Surge, Sway, Heave
Roll, Pitch, Yawm
(°)FDPSO重心处的纵荡运动 F1～ F16 kN #1锚链所受的轴向载荷 Acc.X1, Acc.Y1, Acc.Z1 m/s2 船体舯部位置纵向、
横向、垂向运动加速度Acc.X2 , Acc.Y2, Acc.Z2 m/s2 船体一侧纵向、
横向、垂向运动加速度W1 m 水池模型前方波浪波面升高 W2 m 水池模型一侧波浪波面升高 2. 试验结果及分析
2.1 自由衰减测试
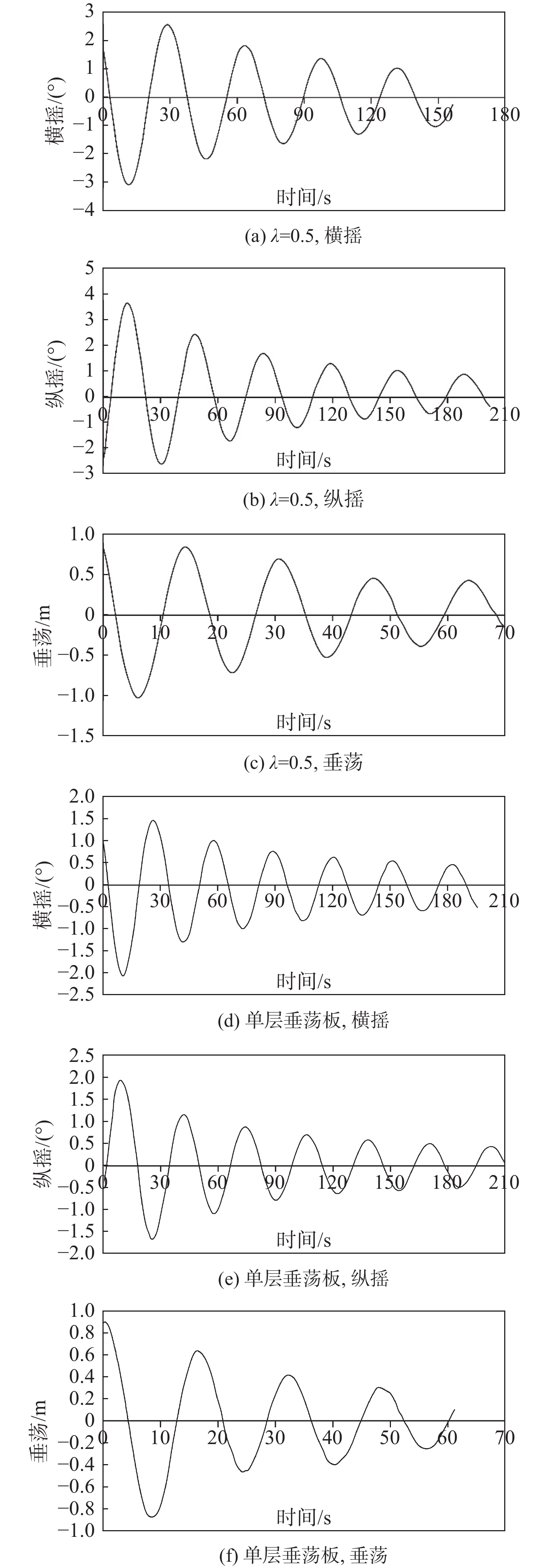
当垂荡板间距λ取0.4，0.5，0.8及为单层垂荡板时，分别对浮体进行垂荡、横摇和纵摇单自由度静水衰减试验，根据测试结果得到最佳的垂荡板间距。针对最佳垂荡板间距，进一步进行浮体与系泊系统整体的纵荡和横荡静水衰减试验，测量得到整体系统的运动固有周期和无因次阻尼比（阻尼与临界阻尼的比值）。由于数据较多，只展示λ=0.5时的自由衰减曲线，如图4所示，测试结果统计如表7所示。
表 7 FDPSO静水衰减试验结果Table 7. FDPSO hydrostatic decay test results试验
序号垂荡板间距λ 试验内容 固有周期/s 无因次
阻尼比15 0.4 横摇衰减 33.509 0.026 8 16 0.4 纵摇衰减 34.694 0.031 6 17 0.4 垂荡衰减 15.771 0.035 18 0.5 横摇衰减 33.687 0.027 1 19 0.5 纵摇衰减 35.043 0.048 8 20 0.5 垂荡衰减 16.414 0.046 2 21 0.8 横摇衰减 33.982 0.044 5 22 0.8 纵摇衰减 35.074 0.051 4 23 0.8 垂荡衰减 16.538 0.044 6 24 单层垂荡板 横摇衰减 31.278 0.035 5 25 单层垂荡板 纵摇衰减 32.239 0.036 9 26 单层垂荡板 垂荡衰减 15.856 0.058 1 27 0.5 纵荡衰减 224.478 0.084 3 28 0.5 横荡衰减 217.871 0.045 9 试验结果表明，固有周期及无因次阻尼比随垂荡板间距的增加而增大，均远离正常波浪作用的频率范围。单层垂荡板三自由度运动的固有周期最小，其纵摇和横摇无因次阻尼比与垂荡板间距λ=0.4时结果相近，垂荡无因次阻尼比要大于双层垂荡板设置时垂荡的情况。究其原因，在垂荡板间距过小时，板与板之间的遮蔽作用过大，绕流效果不理想。同时垂荡板间距过大也会面临垂荡板出水的问题，所以双层垂荡板设置时，最佳间距定为λ=0.5，后续的水动力测试和运动响应测试均针对垂荡板间距λ=0.5展开测量。
2.2 白噪声测试结果
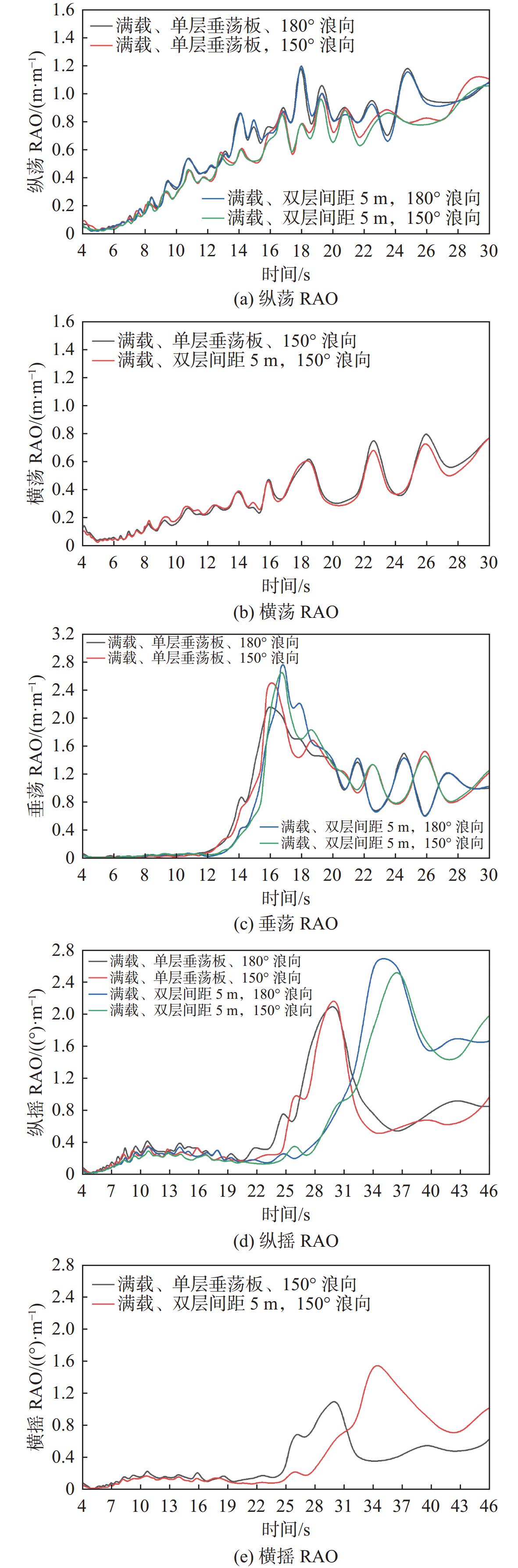
白噪声试验对FDPSO浮体的六自由度时历数据进行实时数据采集与记录，在此基础上进行相关谱分析，即获得所需要的运动响应RAO（为单位幅值规则波作用下的运动响应幅值），结果如图5所示。
可以看出，单层垂荡板， FDPSO垂荡、横摇和纵摇峰值周期分别为15.795 s，30.253 s和32.088 s；双层垂荡板间距λ=0.5，FDPSO垂荡、横摇和纵摇峰值周期分别为16.414 s，33.687 s和35.043 s，这和静水衰减周期基本一致。此外，双层垂荡板这3个自由度的固有周期均大于单层垂荡板情况，同时三自由度响应峰值也均大于单层垂荡板情况。这是由于双层垂荡板引起更大的附连水质量，致使平台三自由度运动周期增大。
2.3 FDPSO系统运动响应
以我国南海海域的环境条件为背景，测试风浪流联合作用下FDPSO动力响应，包括船体运动、系缆力、典型位置的加速度，对比分析了单层垂荡板和λ=0.5双层垂荡板的差异，结果如下所示。
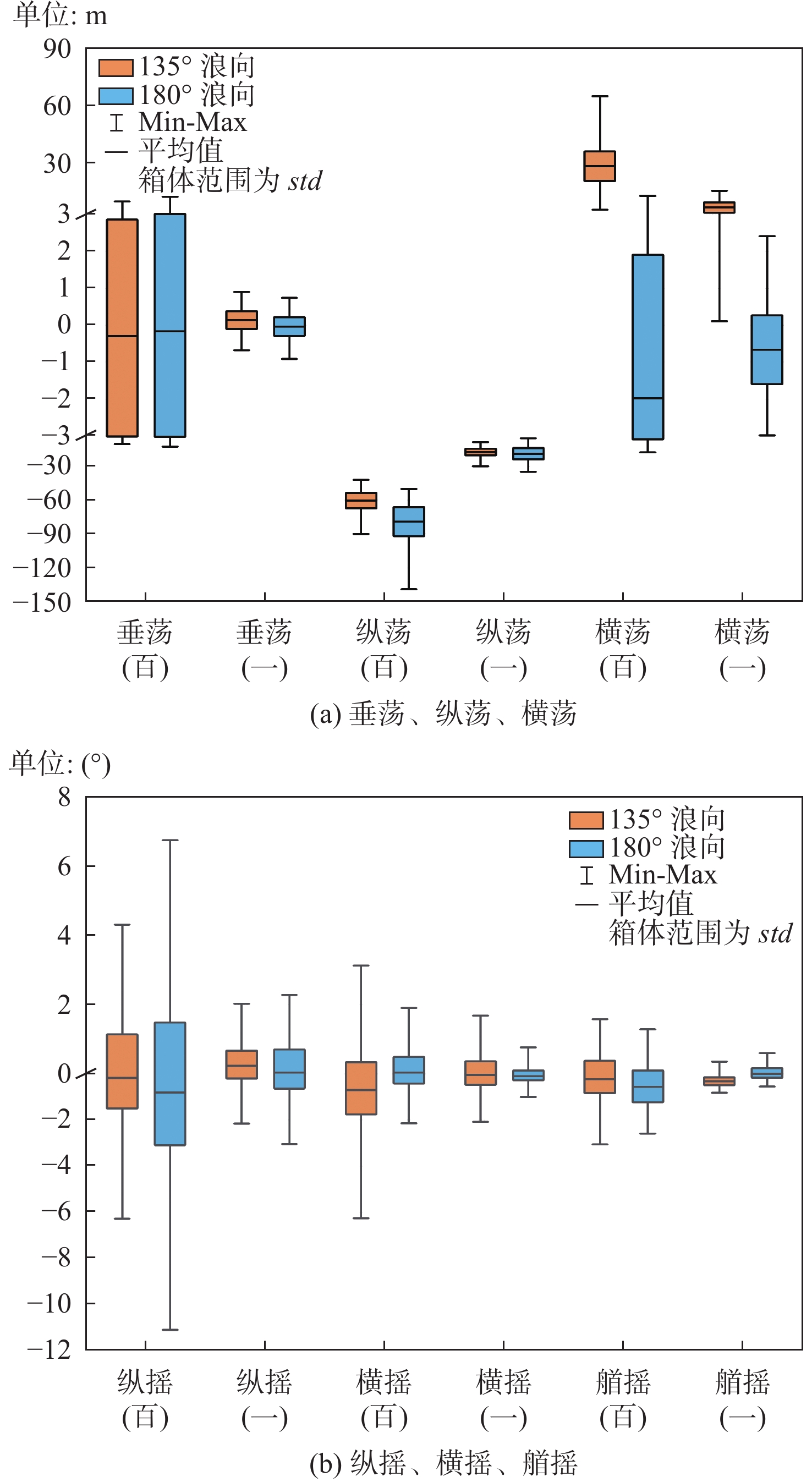
由图6和图7可以看出：双层垂荡板，一年一遇海况，不同的浪向角条件下，船体最大水平漂移距离为29.691 ～34.665 m，垂荡运动极值为0.954 m，纵摇运动极值为3.030°；百年一遇海况，船体出现的最大水平漂移距离为89.814 ～ 138.810 m，垂荡运动极值为12.502 m，纵摇运动极值为12.235°，此时浮体迎浪一侧出现上浪现象运动非常剧烈。对于单层垂荡板，一年一遇海况，船体最大水平漂移距离为32.361 m，垂荡运动极值为0.978 m，纵摇运动极值为2.802°；百年一遇海况，船体出现最大水平漂移距离113.640 m，垂荡运动极值为10.852 m，纵摇运动极值为9.364°。同等环境条件，单层垂荡板船体运动极值接近或小于双层垂荡板船体运动极值，具体如图7所示。
![]()
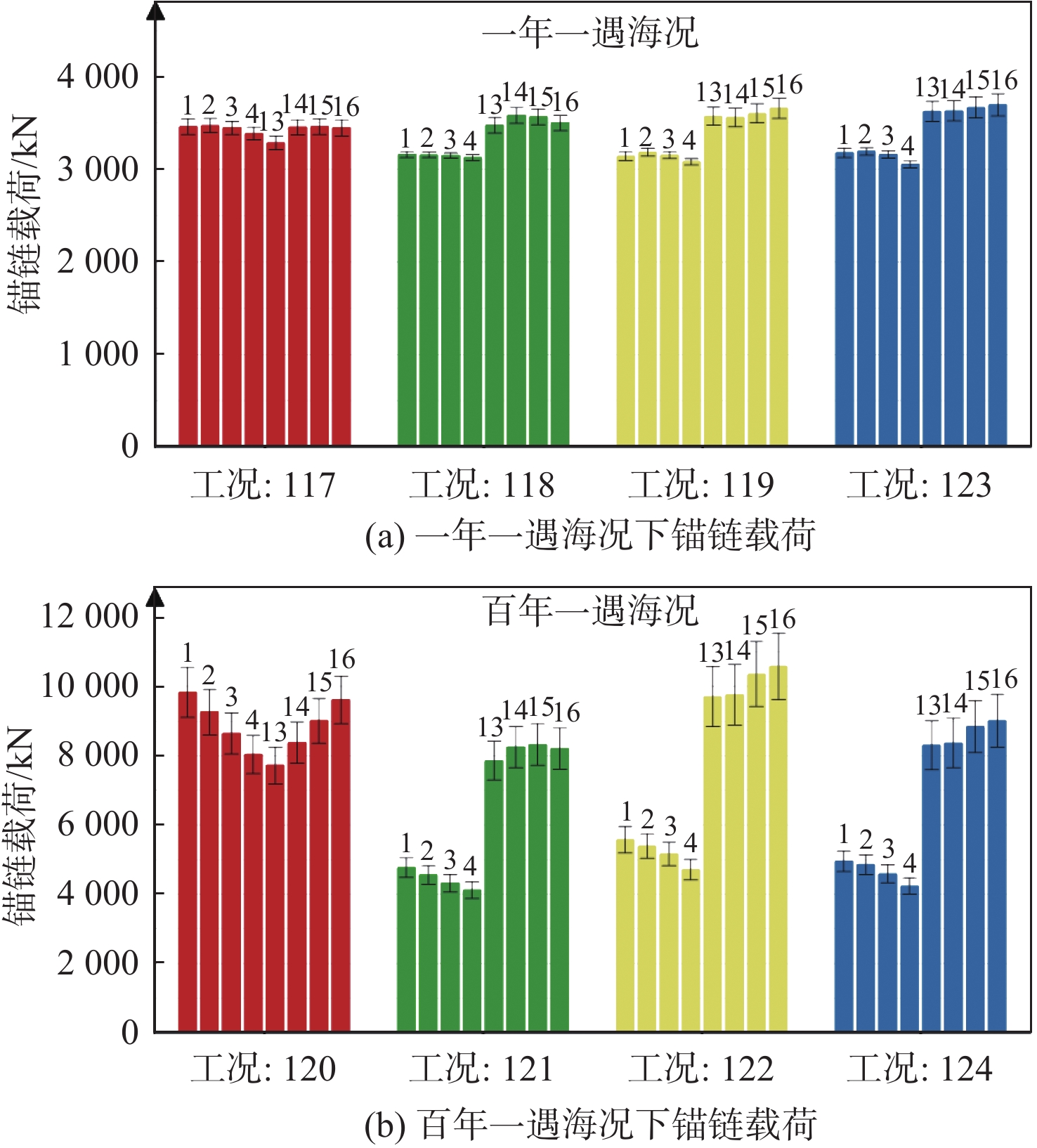
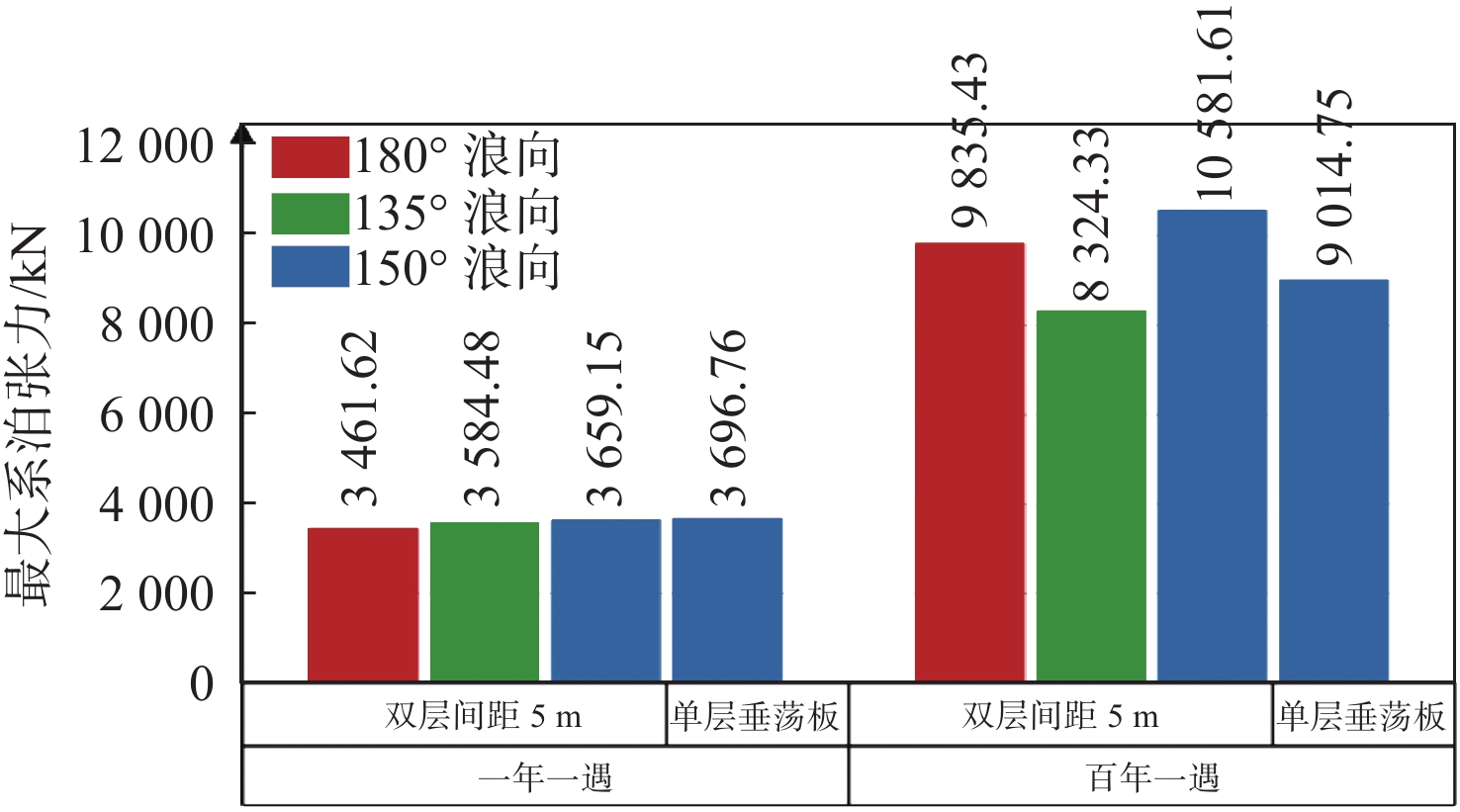
图 7 不同的板设置浮体运动响应（150°浪向）Figure 7. Motion responses of the floats with different plate settings (150° waves)图8和图9统计了FDPSO系缆载荷情况。结果表明，系泊载荷极值出现在150°浪向角、第16号锚链。一年一遇海况，双层垂荡板设置时的系缆载荷极值为3 659.15 kN，单层垂荡板设置时的系缆载荷极值为3 696.76 kN。百年一遇海况，双层垂荡板设置时系缆载荷极值为10 581.61 kN，单层垂荡板设置时的系缆极值为9 014.75 kN，小于双层垂荡板情况。
![]()
图 8 不同海况下各工况锚链载荷Figure 8. Anchor chain loads for each condition in different sea states![]()
图 9 各工况下FDPSO多点系泊系统最大系泊缆张力Figure 9. Maximum mooring cable tension of FDPSO multi-point mooring system under various operating conditions表8统计了FDPSO分别在单层垂荡板和λ=0.5 间距双层垂荡板下，一年一遇和百年一遇海况时，船体运动加速度的统计值，其中Ae表示极值，std表示标准差。测试表明，一年一遇海况船体三自由度加速度远小于百年一遇海况结果；百年一遇海况， FDPSO船体所出现的纵向加速度极值出现在180°浪向、浮体一侧位置，为2.589 m/s2，垂向加速度极值出现在180°浪向、浮体一侧位置，为2.129 m/s2。风浪流同向150°，双层垂荡板纵向加速度极值为3.696 m/s2，单层垂荡板设置时为1.527 m /s2；双层垂荡板垂向加速度极值为2.705 m/s2，单层垂荡板设置时为1.843 m/s2。因此，相同海浪条件下，单层垂荡板时船体的加速度要明显小于双层垂荡板时船体相同位置的加速度。
表 8 加速度测试结果统计Table 8. Acceleration test results一年一遇 百年一遇 运动加速度/(m·s2) Ae std Ae std 垂荡板间距λ=0.5
（180°，风浪流同向）Acc.X1 0.508 0.121 2.589 0.485 Acc.Y1 0.174 0.038 0.609 0.103 Acc.Z1 0.519 0.1 2.129 0.509 Acc.X2 0.544 0.127 2.076 0.412 Acc.Y2 0.158 0.035 0.541 0.112 Acc.Z2 0.23 0.049 1.842 0.449 垂荡板间距λ=0.5
（135°，风浪流不同向）Acc.X1 0.408 0.077 1.726 0.352 Acc.Y1 0.368 0.076 1.26 0.196 Acc.Z1 0.323 0.071 1.828 0.472 Acc.X2 0.435 0.084 1.204 0.242 Acc.Y2 0.353 0.077 1.138 0.183 Acc.Z2 0.174 0.044 1.397 0.389 垂荡板间距λ=0.5
（150°，风浪流同向）Acc.X1 0.47 0.105 3.696 0.657 Acc.Y1 0.361 0.077 4.01 0.431 Acc.Z1 0.371 0.087 2.705 0.485 Acc.X2 0.502 0.108 2.145 0.364 Acc.Y2 0.34 0.071 1.041 0.216 Acc.Z2 0.2 0.049 1.797 0.461 单层垂荡板
（150°，风浪流同向）Acc.X1 0.465 0.092 1.527 0.268 Acc.Y1 0.369 0.067 0.919 0.18 Acc.Z1 0.327 0.074 1.843 0.443 Acc.X2 0.52 0.109 1.456 0.258 Acc.Y2 0.374 0.066 0.913 0.16 Acc.Z2 0.193 0.056 1.559 0.409 3. 结 论
本文采用模型试验测试了FDPSO浮体动力性能。通过自由衰减试验测试不同垂荡板布置时浮体的运动；通过白噪声试验和不规则波试验测试浮体的运动性能。具体工作和结论如下：
1） 单自由度静水衰减试验结果表明，浮体固有周期及无因次阻尼比随垂荡板间距的增加而增大。单层垂荡板浮体运动的固有周期最小，其垂荡无因次阻尼比最大。对于双层垂荡板情况，在垂荡板间距过小时板与板之间的遮蔽作用过大，运动抑制效果不理想；垂荡板间距过大有垂荡板出水问题，所以双层垂荡板的最佳间距定为λ=0.5。
2） 在水平系泊条件下，针对FDPSO分别设置单层垂荡板及λ=0.5间距双层垂荡板的情况，开展不同浪向的白噪声波浪试验，获得FDPSO浮体的RAO。结果表明，λ=0.5间距双层垂荡板下的响应峰值大于单层垂荡板运动响应峰值。
3） 针对λ=0.5 间距双层垂荡板及单层垂荡板浮体开展风浪流联合作用下的运动测试。结果表明，百年一遇海况下浮体垂荡运动剧烈，双层垂荡板有出水情况和上浪现象发生；整体而言单层垂荡板具有更好的运动抑制效果，浮体的运动小于双层垂荡板情况。
4） 一年一遇海况下锚链受力值较小，不同垂荡板设置结果相差不大。百年一遇海况下不同风浪流组合的锚链力差别较大，双层垂荡板情况最大值出现在风浪流同向150°，为10 581.61 kN；单层垂荡板锚链最大锚链力为9 014.75 kN，明显小于双层垂荡板同海况下的最大锚链力。相同海况下，浮体一侧位置的加速度要大于浮体中部位置的加速度；对于风浪流同向150°，单层垂荡板时船体的加速度要明显小于双层垂荡板时船体相同位置的加速度。
本文对于双层垂荡板间距的确定只开展了自由衰减测试，后续还可以进行更详细的试验和分析。
-
![]()
图 7 不同的板设置浮体运动响应（150°浪向）
Figure 7. Motion responses of the floats with different plate settings (150° waves)
![]()
图 8 不同海况下各工况锚链载荷
Figure 8. Anchor chain loads for each condition in different sea states
![]()
图 9 各工况下FDPSO多点系泊系统最大系泊缆张力
Figure 9. Maximum mooring cable tension of FDPSO multi-point mooring system under various operating conditions
表 1 FDPSO船体主尺度参数
Table 1 The main scale parameters of the FDPSO hull
设计参数 符号 实体 模型 总长/m Loa 100 1.667 型宽/m B 100 1.667 型深/m D 40 0.667 吃水/m d 21.4 0.357 排水量/t Δ 107 520 0.544 重心纵向位置/m XG −0.17 −0.003 重心横向位置/m YG 0.37 0.006 重心垂向位置/m KG 24.07 0.401 横摇回转半径/m Rxx 29.52 0.492 纵摇回转半径/m Ryy 29.57 0.493 艏摇回转半径/m Rzz 35.05 0.584 
下载: 导出CSV
表 2 自由衰减测试工况
Table 2 Free decay test conditions
试验序号 垂荡板间距λ 系泊方式 试验内容 15～17 0.4 / 横摇、纵摇、垂荡衰减 18～20 0.5 / 横摇、纵摇、垂荡衰减 21～23 0.8 / 横摇、纵摇、垂荡衰减 24～26 单层垂荡板 / 横摇、纵摇、垂荡衰减 27～28 0.5 4×4 纵荡、横荡衰减
下载: 导出CSV
表 3 FDPSO系统RAO试验工况
Table 3 FDPSO system RAO test conditions
试验序号 垂荡板设置 角度/(°) 113 最佳垂荡板间距 180 114 最佳垂荡板间距 150 115 单层垂荡板 180 116 单层垂荡板 150
下载: 导出CSV
表 4 风、浪、流试验工况
Table 4 Wind, wave and current test conditions
序号 模拟海况 垂荡板 风浪流角度 117 一年一遇 双层，最佳间距 风、浪、流同向180° 118 一年一遇 双层，最佳间距 风、浪135°，流180° 119 一年一遇 双层，最佳间距 风、浪、流同向150° 120 百年一遇 双层，最佳间距 风、浪、流同向180° 121 百年一遇 双层，最佳间距 风、浪135°，流180° 122 百年一遇 双层，最佳间距 风、浪、流同向150° 123 一年一遇 单层 风、浪、流同向150° 124 百年一遇 单层 风、浪、流同向150°
下载: 导出CSV
表 5 环境参数
Table 5 Environmental parameters
海况 有义波高/m 谱峰周期/s 风速/(m·s−1) 流速(m·s−1) 一年一遇 6.2 11.1 19.3 1.05 百年一遇 15 18 49.5 1.95
下载: 导出CSV
表 6 多点系泊FDPSO波浪试验中测量的物理量
Table 6 Physical quantities measured in multi-point moored FDPSO wave tests
测试量 单位 通道说明 Surge, Sway, Heave
Roll, Pitch, Yawm
(°)FDPSO重心处的纵荡运动 F1～ F16 kN #1锚链所受的轴向载荷 Acc.X1, Acc.Y1, Acc.Z1 m/s2 船体舯部位置纵向、
横向、垂向运动加速度Acc.X2 , Acc.Y2, Acc.Z2 m/s2 船体一侧纵向、
横向、垂向运动加速度W1 m 水池模型前方波浪波面升高 W2 m 水池模型一侧波浪波面升高
下载: 导出CSV
表 7 FDPSO静水衰减试验结果
Table 7 FDPSO hydrostatic decay test results
试验
序号垂荡板间距λ 试验内容 固有周期/s 无因次
阻尼比15 0.4 横摇衰减 33.509 0.026 8 16 0.4 纵摇衰减 34.694 0.031 6 17 0.4 垂荡衰减 15.771 0.035 18 0.5 横摇衰减 33.687 0.027 1 19 0.5 纵摇衰减 35.043 0.048 8 20 0.5 垂荡衰减 16.414 0.046 2 21 0.8 横摇衰减 33.982 0.044 5 22 0.8 纵摇衰减 35.074 0.051 4 23 0.8 垂荡衰减 16.538 0.044 6 24 单层垂荡板 横摇衰减 31.278 0.035 5 25 单层垂荡板 纵摇衰减 32.239 0.036 9 26 单层垂荡板 垂荡衰减 15.856 0.058 1 27 0.5 纵荡衰减 224.478 0.084 3 28 0.5 横荡衰减 217.871 0.045 9
下载: 导出CSV
表 8 加速度测试结果统计
Table 8 Acceleration test results
一年一遇 百年一遇 运动加速度/(m·s2) Ae std Ae std 垂荡板间距λ=0.5
（180°，风浪流同向）Acc.X1 0.508 0.121 2.589 0.485 Acc.Y1 0.174 0.038 0.609 0.103 Acc.Z1 0.519 0.1 2.129 0.509 Acc.X2 0.544 0.127 2.076 0.412 Acc.Y2 0.158 0.035 0.541 0.112 Acc.Z2 0.23 0.049 1.842 0.449 垂荡板间距λ=0.5
（135°，风浪流不同向）Acc.X1 0.408 0.077 1.726 0.352 Acc.Y1 0.368 0.076 1.26 0.196 Acc.Z1 0.323 0.071 1.828 0.472 Acc.X2 0.435 0.084 1.204 0.242 Acc.Y2 0.353 0.077 1.138 0.183 Acc.Z2 0.174 0.044 1.397 0.389 垂荡板间距λ=0.5
（150°，风浪流同向）Acc.X1 0.47 0.105 3.696 0.657 Acc.Y1 0.361 0.077 4.01 0.431 Acc.Z1 0.371 0.087 2.705 0.485 Acc.X2 0.502 0.108 2.145 0.364 Acc.Y2 0.34 0.071 1.041 0.216 Acc.Z2 0.2 0.049 1.797 0.461 单层垂荡板
（150°，风浪流同向）Acc.X1 0.465 0.092 1.527 0.268 Acc.Y1 0.369 0.067 0.919 0.18 Acc.Z1 0.327 0.074 1.843 0.443 Acc.X2 0.52 0.109 1.456 0.258 Acc.Y2 0.374 0.066 0.913 0.16 Acc.Z2 0.193 0.056 1.559 0.409
下载: 导出CSV
-
[1] 李焱, 唐友刚, 赵志娟, 等. 新型多筒式FDPSO概念设计及其系泊系统分析[J]. 中国舰船研究, 2013, 8(5): 97–103. doi: 10.3969/j.issn.1673-3185.2013.05.017 LI Y, TANG Y G, ZHAO Z J, et al. Concept design and analysis of the mooring system for the new type of multi-tubular FDPSO[J]. Chinese Journal of Ship Research, 2013, 8(5): 97–103. doi: 10.3969/j.issn.1673-3185.2013.05.017
[2] 蔡晓雄, 芦树平, 秦珩, 等. 第2代Spar平台桁架结构方案设计及优化[J]. 中国舰船研究, 2019, 14(S1): 73–81. doi: 10.19693/j.issn.1673-3185.01575 CAI X X, LU S P, QIN H, et al. Design and optimization of truss structure for the second generation Spar platform[J]. Chinese Journal of Ship Research, 2019, 14(S1): 73–81 (in Chinese). doi: 10.19693/j.issn.1673-3185.01575
[3] 刘利琴, 张晓蕊, 唐友刚, 等. 基于CFD方法的FDPSO锥型垂荡板阻尼特性[J]. 中国海洋平台, 2019, 34(3): 25–31. LIU L Q, ZHANG X R, TANG Y G, et al. Damping characteristics of cone heave plate on FDPSO based on CFD[J]. China Offshore Platform, 2019, 34(3): 25–31 (in Chinese).
[4] 黄孟丽, 李清, 张博, 等. 高海况下浮式生产装置减动结构尺度敏感性分析[J]. 舰船科学技术, 2023, 45(13): 89–95. doi: 10.3404/j.issn.1672-7649.2023.13.018 HUANG M L, LI Q, ZHANG B, et al. Scale-sensitivity analysis for floating production system with anti-motion structure under high sea conditions[J]. Ship Science and Technology, 2023, 45(13): 89–95 (in Chinese). doi: 10.3404/j.issn.1672-7649.2023.13.018
[5] 姚宇鑫. 新概念沙漏型FDPSO主浮体和系泊系统设计方法研究[D]. 大连: 大连理工大学, 2015. YAO Y X. Design and analysis on floating body and mooring system of an innovative sandgla FDPSO[D]. Dalian: Dalian University of Technology, 2015 (in Chinese).
[6] 晏柳, 任慧龙, 孙艳龙, 等. 锚链预张力对FDPSO运动响应的影响[J]. 舰船科学技术, 2017, 39(3): 23–28. doi: 10.3404/j.issn.1672-7619.2017.03.005 YAN L, REN H L, SUN Y L, et al. The effect of mooring line pre-tension on FDPSO's motion[J]. Ship Science and Technology, 2017, 39(3): 23–28 (in Chinese). doi: 10.3404/j.issn.1672-7619.2017.03.005
[7] PHILIP N T, NALLAYARASU S, BHATTACHARYYA S K. Experimental investigation and CFD simulation of heave damping effects due to circular plates attached to spar hull[J]. Ships and Offshore Structures, 2019, 14(4): 396–411. doi: 10.1080/17445302.2013.835146
[8] GONÇALVES R T, MATSUMOTO F T, MALTA E B, et al. Conceptual design of monocolumn production and storage with dry tree capability[J]. Journal of Offshore Mechanics and Arctic Engineering, 2010, 132(4): 041301. doi: 10.1115/1.4001429
[9] LI Y, LI Y L, ZHAO Z M, et al. Dynamic responses of the cylindrical floating drilling production storage and offloading system with annular anti-motion structures under the survival sea scenario[J]. Journal of Marine Science and Engineering, 2023, 11(1): 218. doi: 10.3390/jmse11010218
[10] PINGUET R, BENOIT M, MOLIN B, et al. CFD analysis of added mass, damping and induced flow of isolated and cylinder-mounted heave plates at various submergence depths using an overset mesh method[J]. Journal of Fluids and Structures, 2022, 109: 103442. doi: 10.1016/j.jfluidstructs.2021.103442
[11] SHEN W J, TANG Y G, LIU L Q. Research on the hydrodynamic characteristics of heave plate structure with different form edges of a spar platform[J]. China Ocean Engineering, 2012, 26(1): 177–184. doi: 10.1007/s13344-012-0013-5
[12] NACIRI M. Model test philosophy for FPSO’s in deep Brazilian waters[J]. Marine Systems & Ocean Technology, 2010, 5(2): 91–101. doi: 10.1007/BF03449248
[13] 王世圣, 赵晶瑞, 谢彬, 等. 深水八角形FDPSO总体性能分析[J]. 船海工程, 2014, 43(3): 183–186,189. doi: 10.3963/j.issn.1671-7953.2014.03.045 WANG S S, ZHAO J R, XIE B, et al. Global performance analysis for deep water octagon FDPSO[J]. Ship & Ocean Engineering, 2014, 43(3): 183–186,189. doi: 10.3963/j.issn.1671-7953.2014.03.045
[14] 于晨芳, 胡志强, 王晋. 深水八角形FDPSO垂荡性能数值分析[J]. 中国海洋平台, 2016, 31(1): 23–28. YU C F, HU Z Q, WANG J. Numerical analysis of heave performance for deep water octagon FDPSO[J]. China Offshore Platform, 2016, 31(1): 23–28 (in Chinese).
[15] DENG W R, GUO Y, LIU L Q, et al. Dynamic response analysis of a floating vertical axis wind turbine with helical blades based on the model test[J]. Ocean Engineering, 2023, 273: 113930. doi: 10.1016/j.oceaneng.2023.113930
计量
- 文章访问数: 48
- HTML全文浏览量: 17
- PDF下载量: 0
