0.   引　言

2023年以来，乌克兰频繁使用自杀式无人艇对俄罗斯的舰船、港口、桥梁等重要设施发动突袭，削弱俄罗斯海上防卫力量，并有效牵制了俄军在乌克兰战场的行动。在此背景下，以多无人艇协同目标围捕为代表的柔性对抗技术为海上安全防卫提供了新方向和新范式^[1]。围捕问题本质上是多无人艇协同搜索和发现威胁目标，并以尽可能少的代价（航行距离或能耗）对静态或动态目标实现小于预定距离的包围过程^[2]。

目前，该问题的求解思路主要分为非学习类方法与学习类方法两种^[3]。非学习类协同围捕的研究主要集中在仿生学和博弈论领域，前者启发于自然界动物合作狩猎行为，后者将围捕问题转换为微分对策问题。Fang等^[4]针对开放区域内协同围捕问题，提出基于行为的分布式围捕方法，并根据对抗双方的初始空间分布及速度比推导出捕获条件。刘彦昊等^[5]提出基于狼群优化的围捕策略，通过划分围捕任务给出多个指标的适应度函数，实现对目标的协同围捕。Chen等^[6]利用博弈论研究围捕问题，根据无人艇可达集计算有效围堵点位，基于任务和机动选择建立双层博弈模型，成功围堵高机动目标。Sun等^[7]针对动态环境下的围捕问题，建立基于可达性方法的微分博弈模型，通过求解水平集获得围捕逃跑的前向可达集，得到时间最优轨迹和最优围捕策略。然而，基于仿生学的协同围捕方法适应性不强且通用性受限，同时基于微分博弈理论的协同围捕方法所需要的规则和假设也较多，从而增加了求解最优围捕策略的难度。

学习类协同围捕的研究主要利用多智能体深度强化学习技术，如深度确定性策略梯度、近端策略优化等，通过训练策略网络得到最优的协同围捕行为^[8]。Du等^[9]针对有限区域内协同围捕问题，利用改进的多智能体强化学习进行求解，通过参数共享实现围捕者之间的观测和策略共享。Ma等^[10]提出分布式多智能体强化学习围捕方法，智能体均具有独立的训练网络和执行策略，实现对动态目标的环绕捕获。Kouzeghar等^[11]针对部分可观测的围捕问题，采用集中训练−分布执行强化学习框架，通过全局状态和动作来集中评价围捕性能，依据局部观测分布执行围捕动作。Xia等^[12]设计具有伸缩性与排列不变性的强化学习状态空间，有效缓解系统输入特征维度动态变化的问题。Nantogma等^[13]根据专家知识生成导航子目标集，并利用启发式模型选择目标，通过近端优化策略训练无人艇接近并包围目标。Qu等^[14]为提升多智能体强化学习的围捕效率，利用课程学习设计难度等级不同的任务，由易到难地训练围捕策略。林泽阳等^[15]根据围捕任务的学习难度划分训练数据集，通过逐渐增加样本数据的难度来提高策略训练效率。然而，上述基于多智能体深度强化学习的围捕研究大部分忽略了围捕策略与时间序列的相关性，导致其在动态场景中的适应性不强。此外，上述基于由易到难的课程学习技术虽能够提高训练效率，但其受限于对训练数据或训练场景的划分，难以避免“惰性围捕者”的出现。

在上述问题的推动下，本文拟利用多智能体深度强化学习，提出一种基于阶段诱导学习的多无人艇协同目标围捕策略，旨在实现针对海上目标无人艇智能逃逸的围捕。首先，根据实际应用背景给出多无人艇协同围捕成功的判定条件；其次，将长短时记忆网络（long short-term memory，LSTM）引入Actor及Critic网络，搭建基于多智能体柔性行动−评判（multi-agent soft actor-critic，MASAC）的协同目标围捕训练框架；再次，将围捕过程划分为搜索、围困、捕获这3个阶段，构造基于阶段诱导的围捕奖励，以实现多围捕艇对目标艇的高效围捕。最后，将开展针对3围1的案例对比仿真，验证所提协同目标围捕策略的有效性和优越性。

1.   围捕问题描述

1.1   无人艇运动模型

根据文献[16]，水平面内无人艇的三自由度运动模型可表示为

其中，

式中：$i = 1,2, ... ,n$，表示群体系统中无人艇的序号；${{\boldsymbol{\eta}} _i} = {[{x_i},{y_i},{\psi _i}]^{\mathrm{T}}}$，为大地坐标系下无人艇位置与航向角；${{\boldsymbol{\nu}} _i} = {[{u_i},{v_i},{r_i}]^{\mathrm{T}}}$，为船体坐标系下无人艇纵向速度、横向速度和艏摇角速度；${{\boldsymbol{\tau }}_i} = {[{\tau _{{u}}}_i,0,{\tau _{{{r}}i}}]^{\mathrm{T}}}$，为无人艇控制输入，包括纵向推力和转艏力矩；${{\boldsymbol{\tau}} _{{{{{w}}}}i}} = {[{\tau _{{{{{w}}u}}i}},{\tau _{{{{{{{w}}vi}}}}}},{\tau _{{{{{w}}r}}i}}]^{\mathrm{T}}}$，表示作用在无人艇上的时变环境干扰；${\boldsymbol{R}}({{\boldsymbol{\eta}} _i})$为船体坐标系到大地坐标系的转换矩阵；${\boldsymbol{M}} = {\mathrm{diag}}\left( {{m_{{{u}}i}},{m_{{{v}}i}},{m_{{{r}}i}}} \right)$，为惯性矩阵；标称动力学$\boldsymbol{f}(\boldsymbol{\nu}_i)=[\boldsymbol{f}_{{u}i},\boldsymbol{f}_{{v}i},\boldsymbol{f}_{{r}i}]\mathrm{^{\mathrm{T}}}$。其中，${{\boldsymbol{f}}_{{{u}}i}} = {m_{{{v}}i}}{v_i}{r_i} - {d_{{{u}}i}}{u_i}$，${{\boldsymbol{f}}_{vi}} = - {m_{{{u}}i}}{u_i}{r_i} - {d_{{{v}}i}}{v_i}$，${{\boldsymbol{f}}_{{{r}}i}} = \left( {{m_{{{u}}i}} - {m_{{{v}}i}}} \right){u_i}{v_i} - {d_{{{r}}i}}{r_i}$，其中的${d_{{{u}}i}}$，${d_{{{v}}i}}$和${d_{{{r}}i}}$表示流体阻尼；${m_{{{u}}i}}$，${m_{{{v}}i}}$和${m_{{{r}}i}}$表示3个自由度上的惯性分量^[17]。

1.2   马尔科夫博弈

在协同围捕过程中，可用马尔科夫博弈来描述系统中所有无人艇的强化学习过程^[18]。该博弈过程可用元组$\{ n,S,{A_1},...,{A_n},P,\gamma ,{R_1},...,{R_n}\}$描述，这里的S表示系统状态空间；${A_i}$表示第i艘无人艇的动作空间；P为状态转移概率分布，表示在状态${S_t}$时采取联合动作$[{a_1},...,{a_n}]$后状态转移到${S_{t + 1}}$时的概率；${R_i}$表示第i艘无人艇在状态${S_t}$时采取联合动作后转变为${S_{t + 1}}$得到的奖励。多无人艇协同系统在时刻t时的累积回报为

式中，$\gamma \in [0,1]$为折扣系数。

根据式（1）运动模型可知，每艘无人艇的动作空间均是二维的，则第i艘无人艇在时刻t时的动作可定义为$a_t^i = [{\tau _{{{u}}i}},{\tau _{ri}}]$，所有无人艇的联合动作可表示为$[{\tau _{{{u}}1}},{\tau _{{{r}}1}},...,{\tau _{{{u}}n}},{\tau _{{{r}}n}}]$。无人艇的状态空间需考虑自身、临近艇以及目标艇信息，可通过GPS、陀螺仪和距离传感器获得，则第i艘围捕艇的状态为$s_t^i = [{x_1},...,{x_n},{y_1},...,{y_n},{u_i},{\psi _i},{x_{\rm{T}}},{y_{\rm{T}}},{d_{{\rm{T}}i}}]$，其中，${x_{\rm{T}}}$和${y_{\rm{T}}}$分别表示目标艇的纵向和横向位置，${d_{{\rm{T}}i}}$表示第i艘围捕艇与目标艇之间的相对距离。

1.3   围捕成功判定

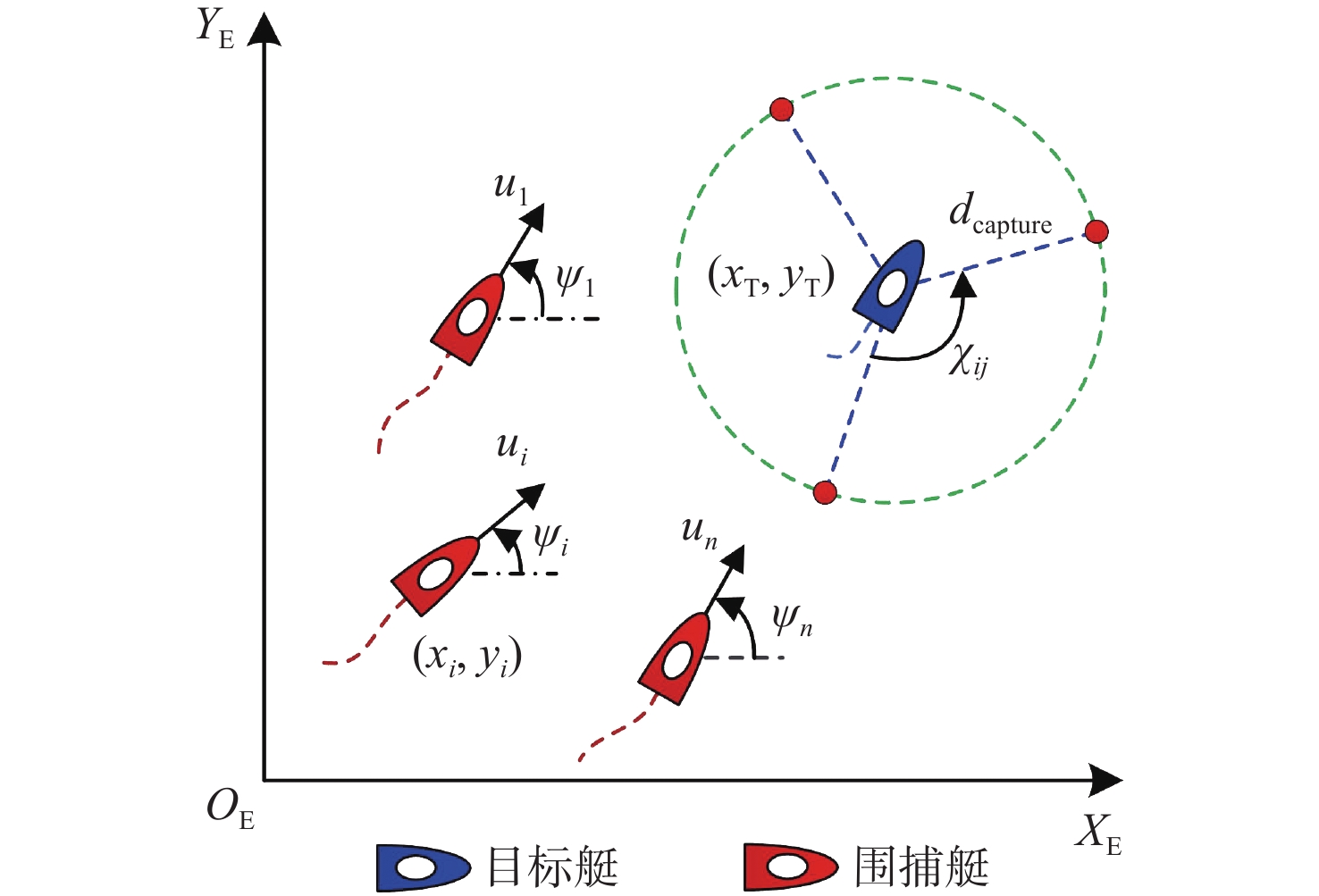
多无人艇协同目标围捕如图1所示，围捕艇在一定区域内执行围捕任务，目标艇具有一定的环境感知和危险规避能力，可根据探测范围内围捕艇位置实现理性逃逸。其中，$({x_i},{y_i})$表示围捕艇位置，${d_{\rm{capture}}}$表示围捕半径，${\chi _{ij}}$表示相邻围捕艇与目标艇连线所形成的围捕角，$i,j \in n$且$i \ne j$。

图  1  多无人艇协同目标围捕示意图

Figure  1.  Cooperative target hunting diagram of multi-USVs

下载: 全尺寸图片 幻灯片

由围捕临界条件可知，理想的围捕包围圈是n艘围捕艇尽可能均匀地分布在目标艇周围。因此，基于距离和角度约束的协同目标围捕成功判定条件可设定为

式中：${d_{\rm{safe}}}$表示安全距离；${\chi _0}$为较小的正常数。

需要注意的是，考虑到无人艇的欠驱动操纵特性及海上复杂干扰影响，在运动过程中形成完全理想的围捕包围圈概率较小。根据文献[8]和文献[12]，围捕角允许存在一定的偏差，即${\chi _0} = {{\text{π}} / {12}}$。此外，目标艇从给定起点匀速运动至给定终点，若在运动过程中感知到围捕艇靠近，则采用人工势场法实现理性规避和逃逸，该逃逸策略可表示为

式中：${{\boldsymbol{v}}_{\rm{T}}}$为目标艇速度向量，且该逃逸速度最大值小于围捕艇速度最大值；${{\boldsymbol{p}}_{\rm{T}}}$和${{\boldsymbol{p}}_i}$分别为目标艇位置和围捕艇位置。

2.   基于阶段诱导的多智能体柔性行动−评判围捕学习

2.1   多智能体柔性行动−评判设计

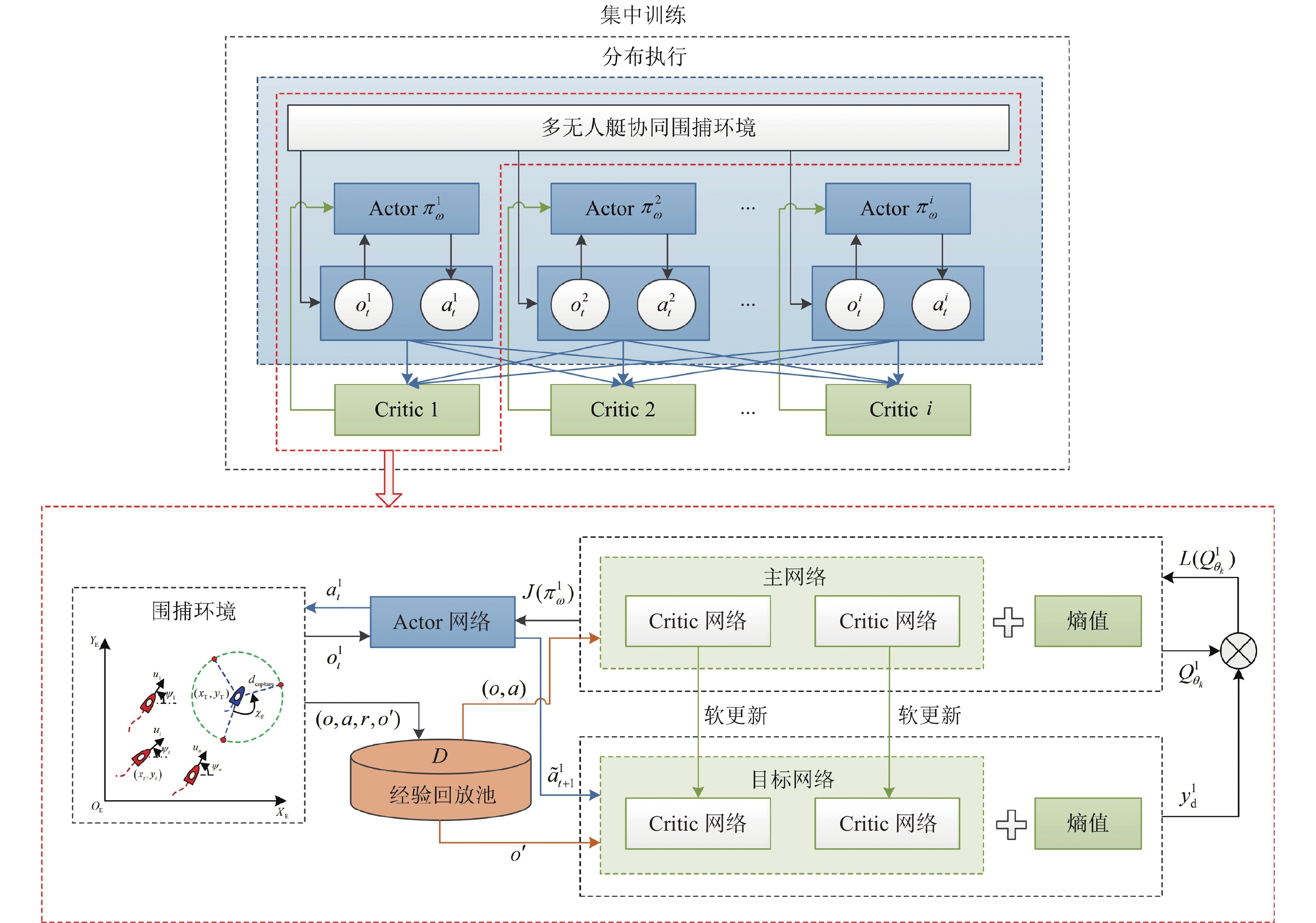
面向多无人艇协同目标围捕任务，考虑每艘无人艇策略变化导致训练不稳定的问题，利用最大熵机制和集中式训练−分布式执行学习框架，设计基于多智能体柔性行动−评判的协同目标围捕策略，实现高维连续动作空间下多围捕艇同时训练，如图2所示。在集中式训练中，每艘无人艇的Critic网络能够获取所有无人艇的状态值和动作值，其输出是对全局围捕态势的评估，避免个体非完全观测导致的群体协调能力不足。在分布式执行中，无需Critic网络，每艘无人艇的Actor网络根据局部观测信息执行各自的策略，保证协同目标围捕策略的可扩展性。

图  2  基于多智能体柔性行动−评判的协同目标围捕训练框架

Figure  2.  Training framework for cooperative target hunting based on multi-agent soft actor-critic

下载: 全尺寸图片 幻灯片

首先，设计第i艘围捕艇的Actor网络$\pi _\omega ^i$，其输出为高斯分布的均值和标准差，通过重参数化形成策略函数${{\boldsymbol{f}}_{{\omega ^i}}}(o_t^i,\chi )$，利用采样获得动作值

式中：$\xi$表示高斯噪声；${\omega ^i}$为第i艘围捕艇的Actor网络参数；${\theta _{{\omega ^i}}}(o_t^i)$表示均值；${\delta _{{\omega ^i}}}(o_t^i)$表示方差。

多智能体柔性行动−评判的目标是寻找随机策略，引导无人艇在尽可能大的范围内探索，避免陷入局部最优，最大化累积回报以及策略的熵。基于此，Actor网络参数更新的目标函数表示为

式中：熵值$H(\pi _\omega ^i( \cdot |o_t^i)) = - {\mathbb{E}_D}\log (\pi _\omega ^i(a_t^i|o_t^i))$，其中，$o_t^i$表示第i艘围捕艇在t时刻的观测信息，且该时刻所有围捕艇观测信息的集合为$o = \{ o_t^1,o_t^2, ...,o_t^i\}$，以及动作集合为$a = \{ a_t^1,a_t^2,...,a_t^i\}$；$\mathop {\min }\limits_{k = 1,2} Q_{{\theta _k}}^i(o,a)$表示围捕艇主网络中两个Critic网络产生动作价值中的较小值，其中${\theta _k}(k = 1,{\text{ }}2)$表示Critic的网络参数；D表示经验回放池，每组经验数据均以元组$\left\{ {o,a,r,o'} \right\}$的形式储存，其中，$r = \{ r_t^1,r_t^2,...,r_t^i\}$表示该时刻下每艘围捕艇的奖励集合，$o'$为下一时刻的观测信息集合；${\alpha _i} > 0$，表示正则化系数，通过最小化损失函数更新为

式中，${H_{\rm{d}}}$为设定的熵阈值。

接着，设计第i艘围捕艇的Critic网络。该网络通过全局的观测信息和动作信息评估当前的围捕态势，其网络参数通过最小化损失函数更新为

式中，$y_{\rm{d}}^i$表示目标值，可以写为

式中：$\mathop {\min }\limits_{k = 1,2} Q_{{{\bar \theta }_k}}^i(o',\tilde a')$表示两个目标Critic网络产生动作价值中的较小值；${\bar \theta _k}(k = 1,{\text{ }}2)$为目标Critic网络参数；$\tilde a' = \{ \tilde a_{t + 1}^1,\tilde a_{t + 1}^2 ,...,\tilde a_{t + 1}^i\}$，其中动作值${\tilde a^i}_{t + 1}$是由策略在$t + 1$时刻采样获得，即$\tilde a_{t + 1}^i \sim \pi _\omega ^i( \cdot |o_{t + 1}^i)$，而非来自经验回放池。

为保证高效和稳定的围捕学习，采用软更新方式更新第i艘围捕艇的目标网络，则有

式中，$\sigma$表示目标网络更新率。

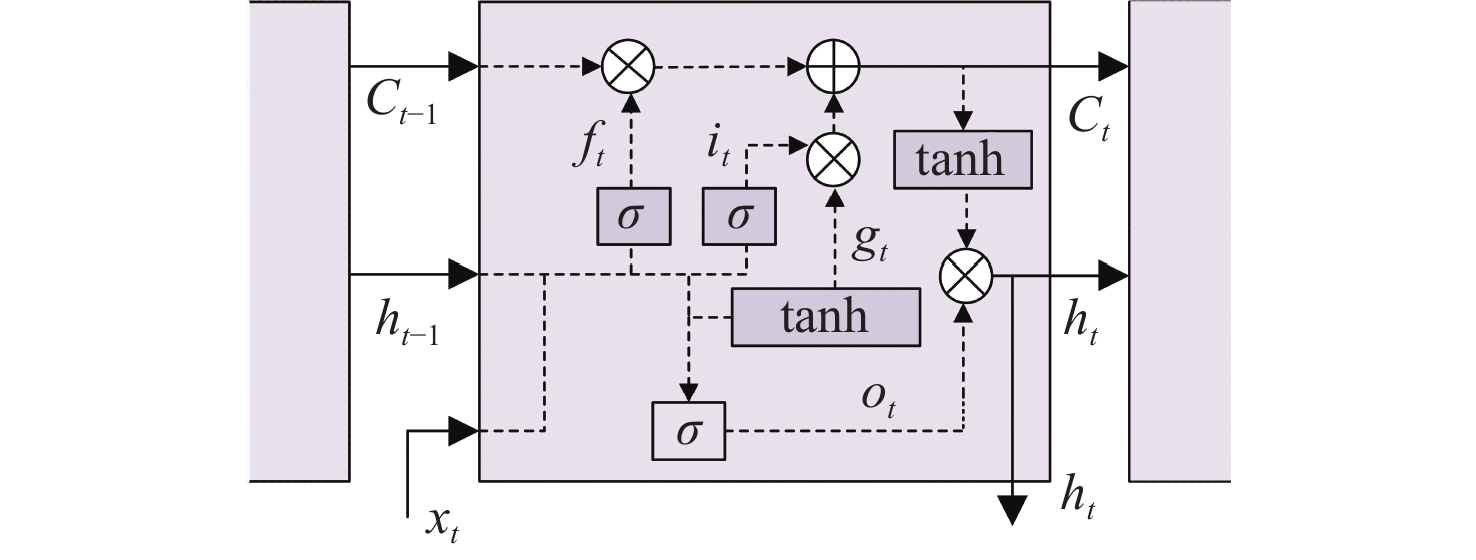
最后，考虑多无人艇协同目标围捕历史状态信息对训练性能的影响，利用具有“记忆”功能的LSTM网络改善神经网络结构，以高效处理状态序列信息并做出更稳健的决策。LSTM网络结构如图3所示，${{\boldsymbol{x}}_t}$，${{\boldsymbol{h}}_t}$和${{\boldsymbol{C}}_t}$分别为当前时刻的输入状态、单元输出和单元状态；${{\boldsymbol{f}}_t}$，${{\boldsymbol{i}}_t}$和${{\boldsymbol{o}}_t}$分别为遗忘门输出、输入门输出和输出门输出，其更新过程表示为

图  3  LSTM网络结构图

Figure  3.  Architecture diagram of LSTM network

下载: 全尺寸图片 幻灯片

式中：$\rm{sig}$表示sigmoid函数；tanh表示双曲正切函数；$\odot$表示哈达玛积运算；${{\boldsymbol{W}}_i}(i = 1,2,...,8)$为权重矩阵；${{\boldsymbol{b}}_j}(j = 1,2,...,4)$为偏置项。

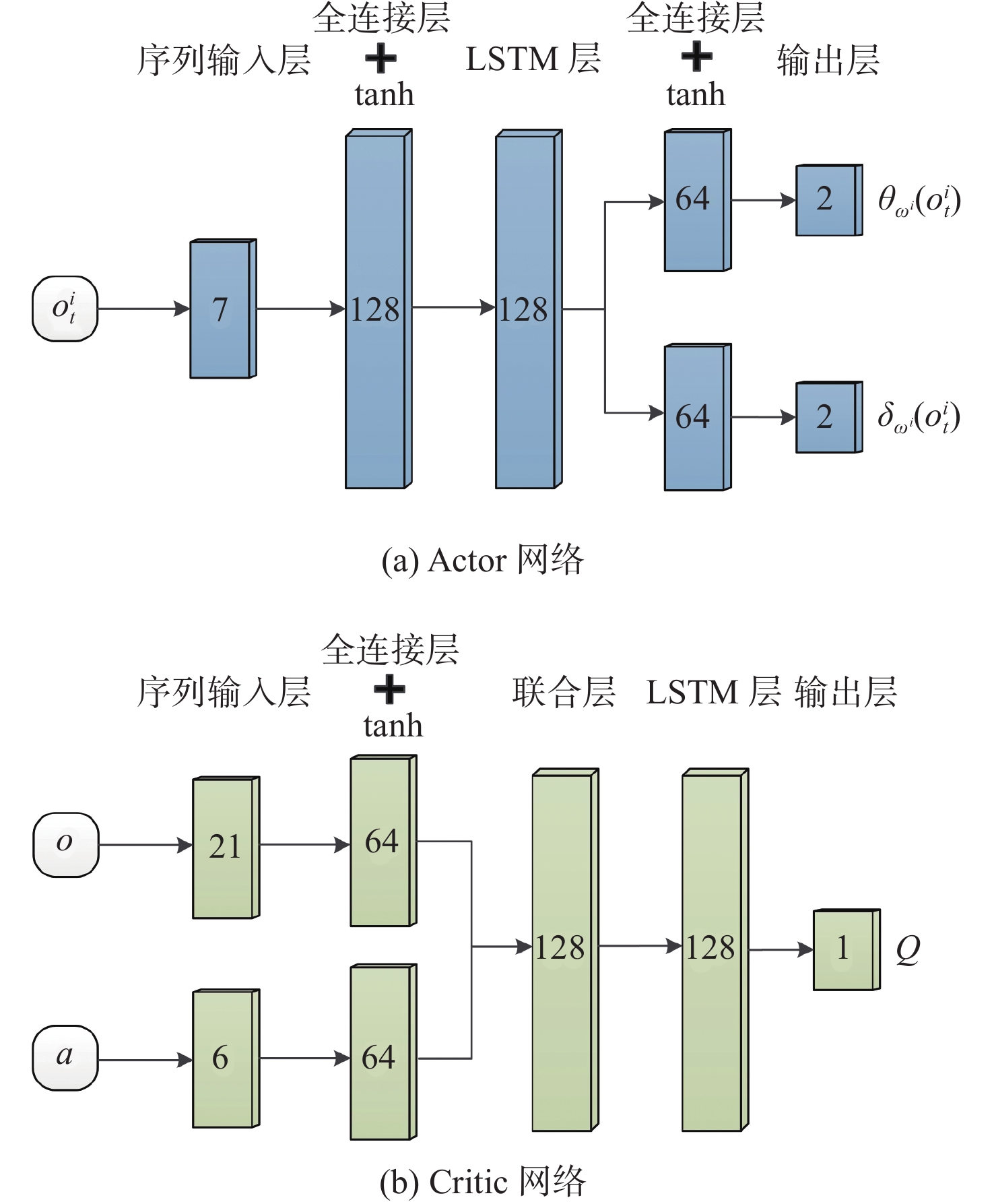
在此基础上，构建基于LSTM的Actor网络和Critic网络，其网络结构如图4所示。Actor网络根据输入的局部观测信息产生均值和方差，Critic网络根据输入的全局观测与动作信息产生动作价值函数值。

图  4  神经网络结构图

Figure  4.  Neural network architecture diagram

下载: 全尺寸图片 幻灯片

基于多智能体柔性行动−评判的协同目标围捕训练流程如下所示，其中的${\lambda _ * }$表示学习率，满足$0 < {\lambda _ * } < 1$。

2.2   阶段诱导围捕奖励设计

由1.3节的围捕目标和判定条件可知，多无人艇协同目标围捕问题包括群体围捕目标和个体行为操纵两个子问题，故需要两类奖励函数来评估围捕艇的当前状态，即协同围捕奖励与个体操纵奖励。

首先，针对协同目标围捕，利用由易到难的课程学习范式，设计一种多阶段诱导的奖励函数，通过双方当前状态来优化围捕训练进程，避免“惰性无人艇”的出现并提高围捕成功率。根据围捕艇和目标艇的位置关系，将协同围捕任务划分为3个阶段，其判定条件如图5所示。第1阶段为搜索阶段，围捕艇学会迅速靠近目标；第2阶段为围困阶段，围捕艇学会对目标形成初步的围捕态势；第3阶段为捕获阶段，围捕艇均处于围捕半径内，并均匀地分布在目标周围。

图  5  阶段诱导围捕奖励判定

Figure  5.  Stage-induced hunting reward determination

下载: 全尺寸图片 幻灯片

搜索阶段的判定条件为

式中，${S_{( * )}}$表示由无人艇位置点围成区域的面积。基于此，设计搜索阶段诱导的围捕奖励为

式中，${k_0} > 0$。

围困阶段的判定条件为：

式中：$0 < {k_1} < 1$；${d_{ij}}$表示第i艘围捕艇与第j艘围捕艇之间的相对距离。为保证目标位于由围捕艇围成的多边形区域内，设计围困阶段诱导的围捕奖励为

式中：${k_2} > 0$；${k_3} > 0$；$j = i + 1$。

捕获阶段的判定条件为：

式中，max表示最大值。为保证围捕艇均位于围捕半径内，以及尽可能地均匀分布在目标艇周围，设计捕获阶段诱导的围捕奖励为

式中：${k_4} > 0$；${\varphi _i} = \arctan 2\left( {\left( {{y_i} - {y_{\rm{T}}}} \right),\left( {{x_i} - {x_{\rm{T}}}} \right)} \right)$。

结合式（14）、 式（16）以及式（18）的奖励，针对协同目标围捕的阶段诱导围捕奖励可以写为

接着，针对协同围捕过程中的个体行为操纵，考虑无人艇之间的碰撞和系统控制输入约束，当${d_{{\rm{T}}i}} < {d_{\rm{safe}}}$或${d_{ij}} < {d_{\rm{safe}}}$时，设计碰撞奖励为

式中：$\min$表示最小值；${k_5} > 0$；${k_6} > 0$；${d_{\rm{safe}}}$表示无人艇之间的安全距离。

此外，为缓解无人艇前后时刻控制输入差值过大引起的系统抖振现象，设计输入约束奖励为

在此背景下，第i艘围捕艇在t时刻的协同目标围捕奖励可写为

需要注意的是，通过阶段诱导围捕奖励开展多智能体强化学习，可以避免“惰性无人艇”的出现，即群体中的个别无人艇一旦学习到较好的策略并完成围捕任务时，其他无人艇不需要执行策略就可以获得“虚假奖励”。

值得一提的是，当无人艇个数$n = 3$时，捕获阶段诱导围捕奖励中的$g({\varphi _i})$可写为

结果表明，当围捕角越接近${{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. } 3}$，所获得的奖励越大，即满足围捕成功判定式（4）中的第2个条件。

3.   仿真验证

为验证所提围捕策略的有效性和优越性，开展针对无人艇Cybership Ⅱ的3围1仿真，当满足式（4）条件时判定围捕成功，其中无人艇对应式（1）的运动模型参数见文献[19]。仿真环境为Windows11，搭载CPU为Intel(R) Core(TM) i7-14700KF，显卡为NVIDIA GeForce RTX 4070 SUPER，基于Python 3.9.18搭建二维围捕空间，同时使用Pytorch 2.4.0深度学习框架进行协同目标的围捕训练。

在给定范围内随机初始化围捕艇的位置和航向角，${x_i} \in [ - 110, - 30]$，${y_i} \in [ - 70,10]$，${\psi _i} \in [0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}]$，$i = 1,{\text{ }}2,{\text{ }}3$。目标艇从起点（0，120）匀速运动至终点（125，−90），速度大小恒为1；若在运动过程中感知到围捕艇靠近，即$\min {d_{{\rm{T}}i}} \leqslant 25$时，则采用式（5）的逃逸策略进行理性规避，且最大逃逸速度为1.5。围捕半径${d_{\rm{capture}}} = 15$，安全距离${d_{\rm{safe}}} = 5$，围捕艇的速度最大值为2.3。阶段诱导围捕系数${k_0} = 0.01$，${k_1} = 0.8$，${k_2} = 0.1$，${k_3} = 5$，${k_4} = 10$，${k_5} = 100$，${k_6} = 100$。参考文献[20]对训练主要超参数进行设置，具体数值如表1所示。

表  1  训练主要超参数设定

Table  1.  Main hyper-parameter settings for training

参数	数值
折扣系数$\gamma$	0.99
最大训练轮次F	5 000
每轮次训练最大步数K	1 000
仿真步长/s	0.5
Critic网络学习率$\lambda\mathrm{_{cr}}$	0.000 3
Actor网络学习率$\lambda\mathrm{_{ac}}$	0.000 2
熵学习率$\lambda_{\mathrm{en}}$	0.000 5
目标网络更新率$\sigma$	0.000 2
熵阈值${H_{\rm{d}}}$	−2
优化器	Adam
mini-batch数量N	256
序列长度	20
经验回放池大小	1 000 000

下载: 导出CSV 

| 显示表格

不失一般性，采用一阶马尔科夫过程来模拟时变环境干扰，其形式为

式中：${\alpha _{ * i}}$为正常数；${w_{ * i}}$表示高斯白噪声过程，*表示u，v，r；$G(s) = {{0.255s} / {\left( {{s^2} + 0.485s + {{0.8}^2}} \right)}}$表示传递函数。

分别使用MASAC^[21]，MASAC结合LSTM网络^[22]（MASAC+LSTM），MASAC结合阶段诱导奖励（MASAC+SI)，MASAC结合LSTM网络和阶段诱导奖励（MASAC+LSTM+SI）训练多无人艇协同目标围捕策略，最大训练轮次为5 000次。不同策略下的训练过程曲线如图6所示，包括多无人艇协同围捕奖励、各无人艇围捕奖励，以及围捕成功率。

图  6  不同策略下协同目标围捕性能对比

Figure  6.  Performance comparisons of cooperative target hunting under different strategies

下载: 全尺寸图片 幻灯片

图6（a）和图6（b）中实线表示滑动平均奖励值，滑动窗口大小为100，阴影部分则表示每轮训练的实际奖励。由图6（a）可知，在围捕艇协同探索环境的过程中，4种策略的奖励曲线在训练前期均趋于上升趋势，且在2 300轮次之后处于收敛状态。但是，在0～2 300轮次之间，本文提出的围捕策略奖励获取效率明显高于其他3种策略，且收敛后的平均奖励值相较MASAC+SI提升约9.5%，相较MASAC+LSTM提升约19.4%，相较MASAC提升约90.7%。由图6（b）可知，在本文所提出的MASAC+LSTM+SI策略下，各艘围捕艇的奖励曲线在训练前期呈上升趋势，且最终全部完成收敛，并未出现“虚假奖励”现象。围捕成功率曲线如图6（c）所示，在达到最大训练轮次时，４种策略的围捕成功率分别为94.6%，91.3%，88.5%和70.2%，本文策略相比MASAC+SI增加3.3%，相比MASAC+LSTM增加6.1%，相比MASAC增加24.4%。特别地，在0～1 500轮次，MASAC+LSTM与MASAC的平均奖励和成功率之间差异较小，而1 500轮次之后前者收敛速度和终值明显优于后者。这是因为引入LSTM网络，增强围捕艇利用历史信息的能力，进而提升了策略性能。

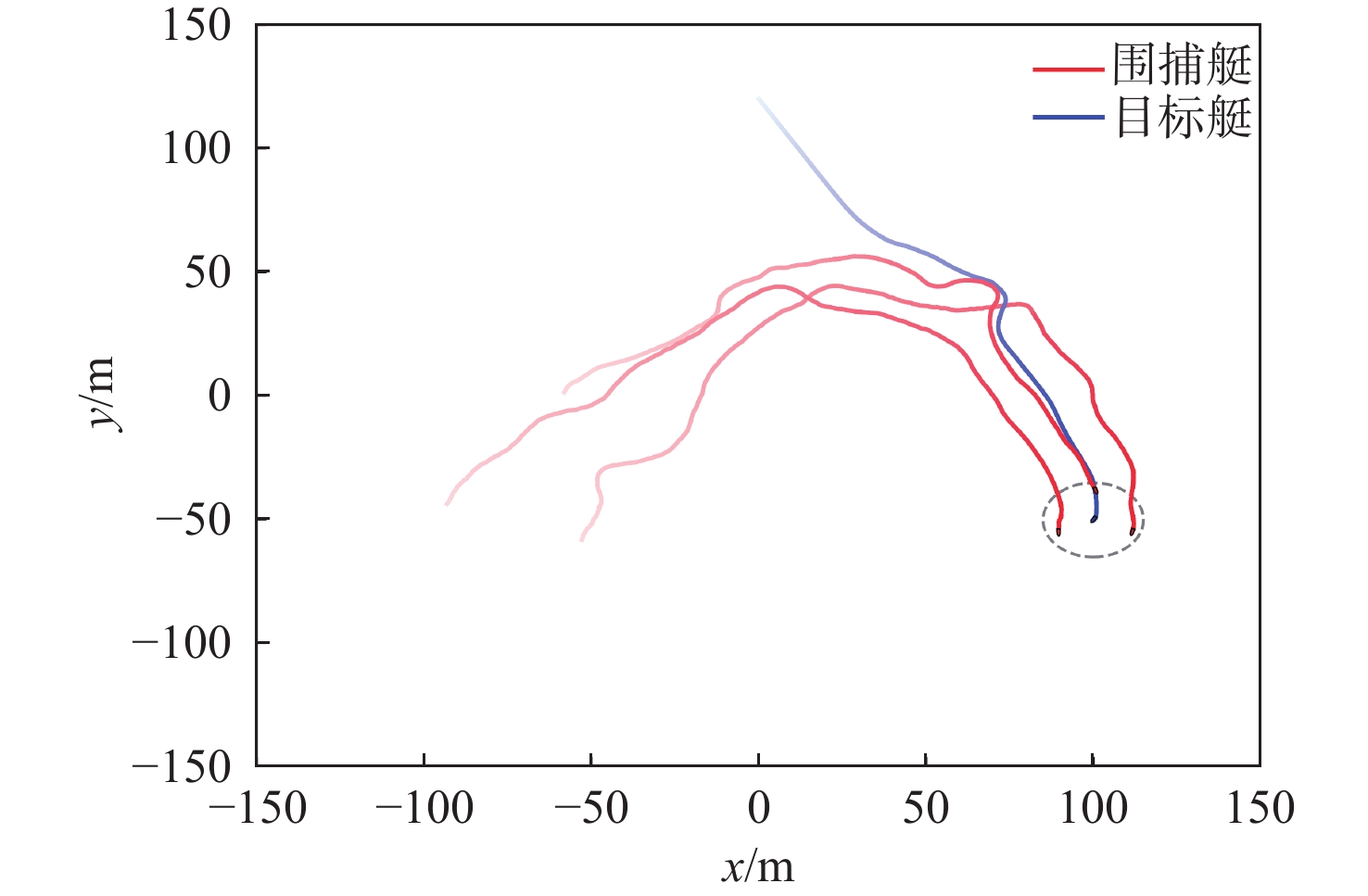
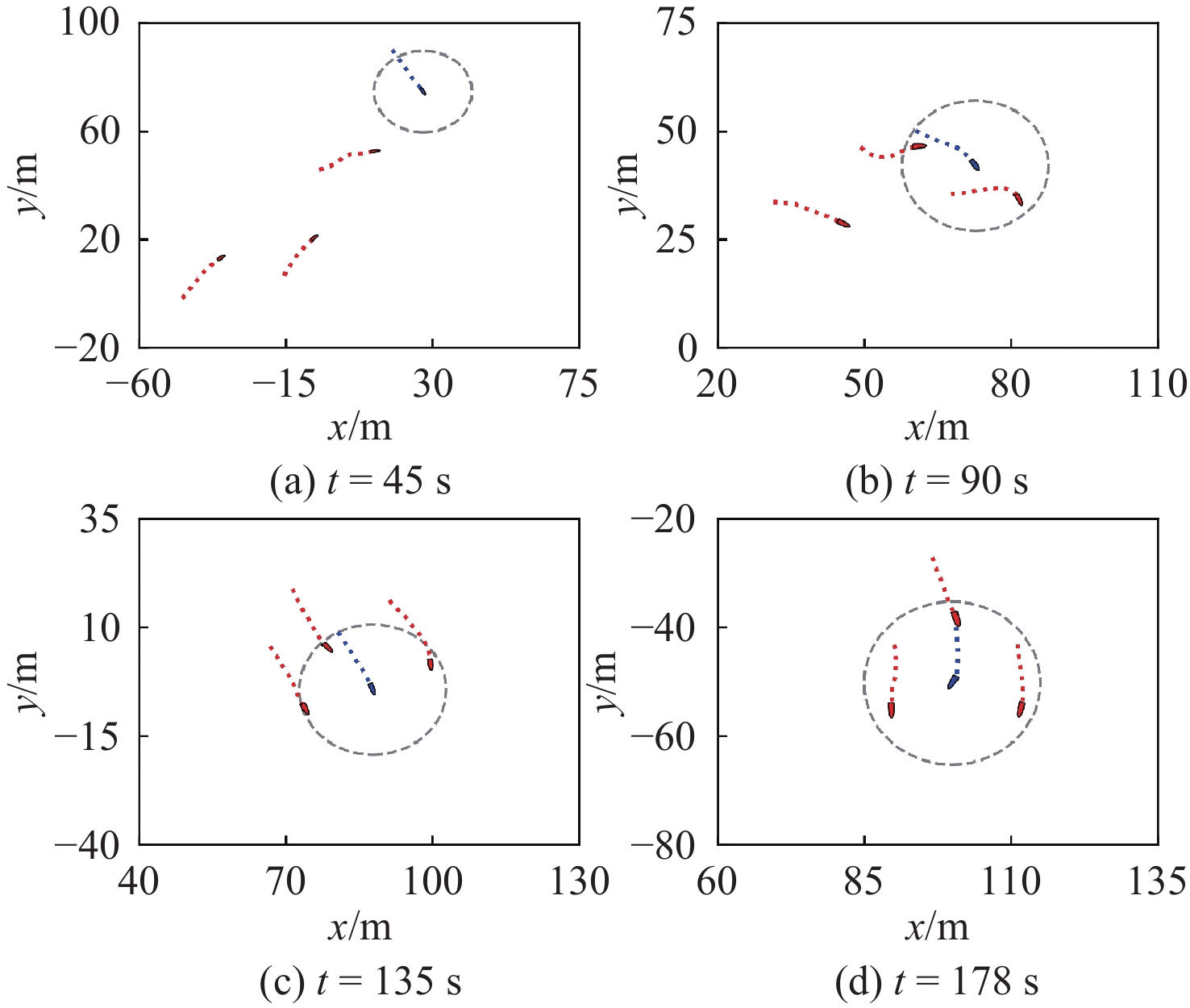
训练完成后，保存围捕成功的Actor网络参数，采用本文策略进行围捕测试。测试环境与训练环境相同。图7和图8分别给出多无人艇协同目标围捕行为和不同时刻的轨迹。从图中可以看出，在t = 45 s时刻，围捕艇搜索并逐渐靠近目标，此时的目标行为不受围捕艇影响。在t = 90 s和t = 135 s时刻，围捕艇对目标进行追击、围堵和拦截，形成初步围捕态势，而目标艇采取式（5）的策略进行逃逸。在t = 178 s时刻，围捕艇以“夹击”态势成功捕获目标。

图  7  多无人艇协同目标围捕行为

Figure  7.  Cooperative target hunting performance of multi-USVs

下载: 全尺寸图片 幻灯片

图  8  不同时刻的围捕−逃逸轨迹

Figure  8.  Hunting and escaping trajectories at different times

下载: 全尺寸图片 幻灯片

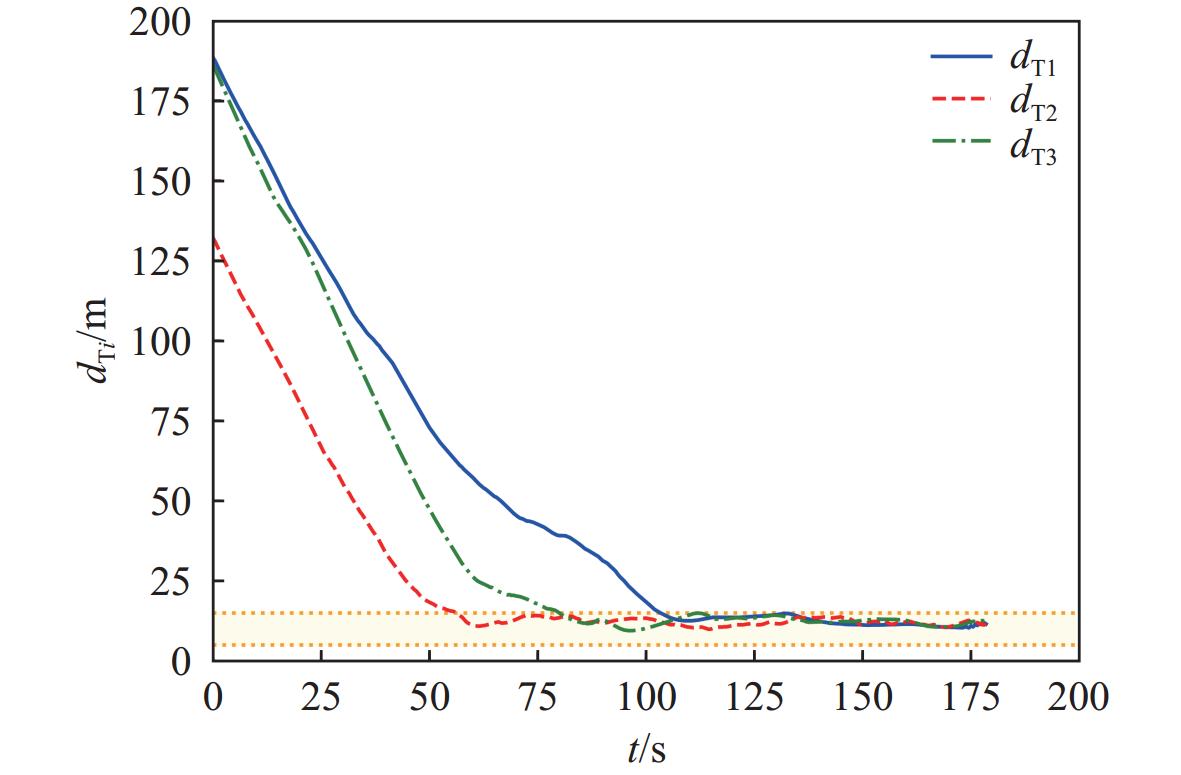
图9给出围捕艇和目标艇的相对距离，阴影部分表示双方距离满足${d_{\rm{safe}}} \leqslant {d_{{\rm{T}}i}} \leqslant {d_{\rm{capture}}}$。3艘围捕艇分别在t = 56 s，t = 80 s和t = 103 s时刻先后进入到此围捕区域内，之后便维持在该范围内。在满足围捕成功判定条件中的距离约束后，围捕艇开始尝试对目标进行捕获。

图  9  围捕艇和目标艇的相对距离

Figure  9.  Distances between hunting USVs and the target

下载: 全尺寸图片 幻灯片

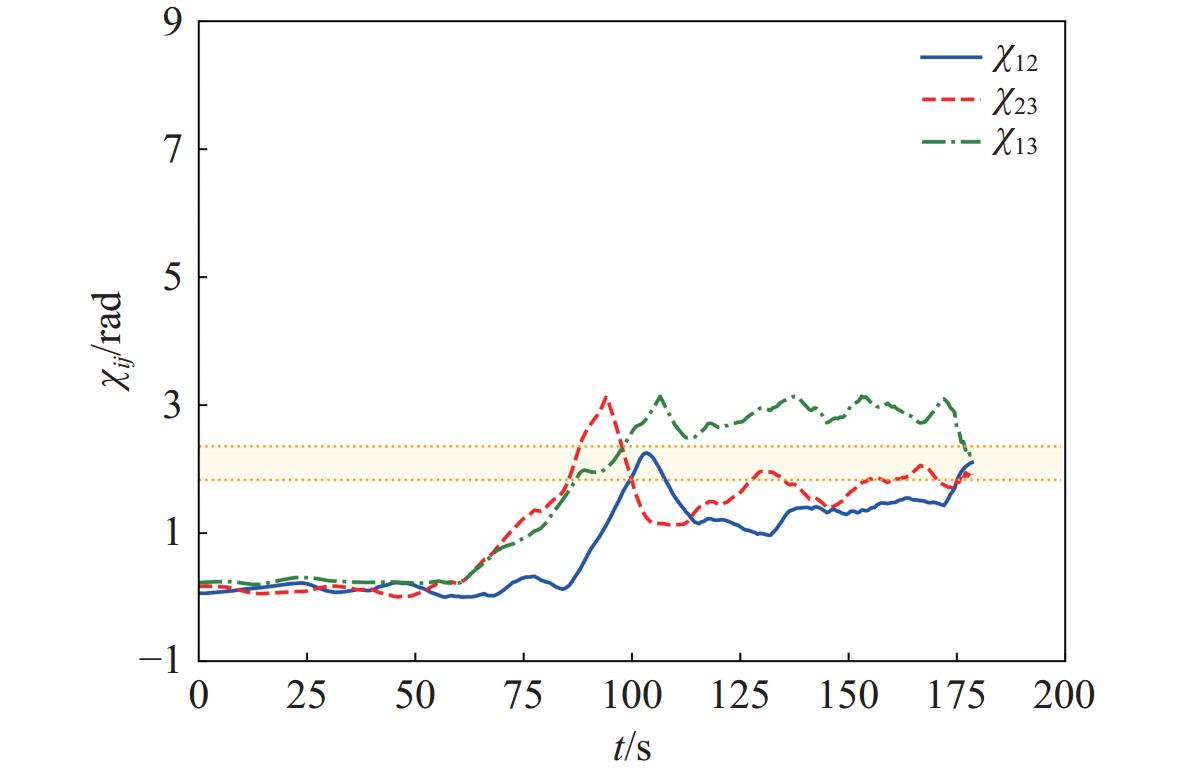
图10所示为临近围捕艇的围捕角，阴影部分表示围捕角满足${\chi _{ij}} \in [{{2{\text{π}} } \mathord{\left/ {\vphantom {{2{\text{π}} } 3}} \right. } 3} - {\chi _0},{{2{\text{π}} } \mathord{\left/ {\vphantom {{2{\text{π}} } 3}} \right. } 3} + {\chi _0}]$，围捕艇在保持围捕距离的前提下自组织调整围捕角，在t = 178 s时刻满足围捕成功判定中的角度约束，成功捕获目标。

图  10  临近围捕艇间的围捕角

Figure  10.  Hunting angles between adjacent hunting USVs

下载: 全尺寸图片 幻灯片

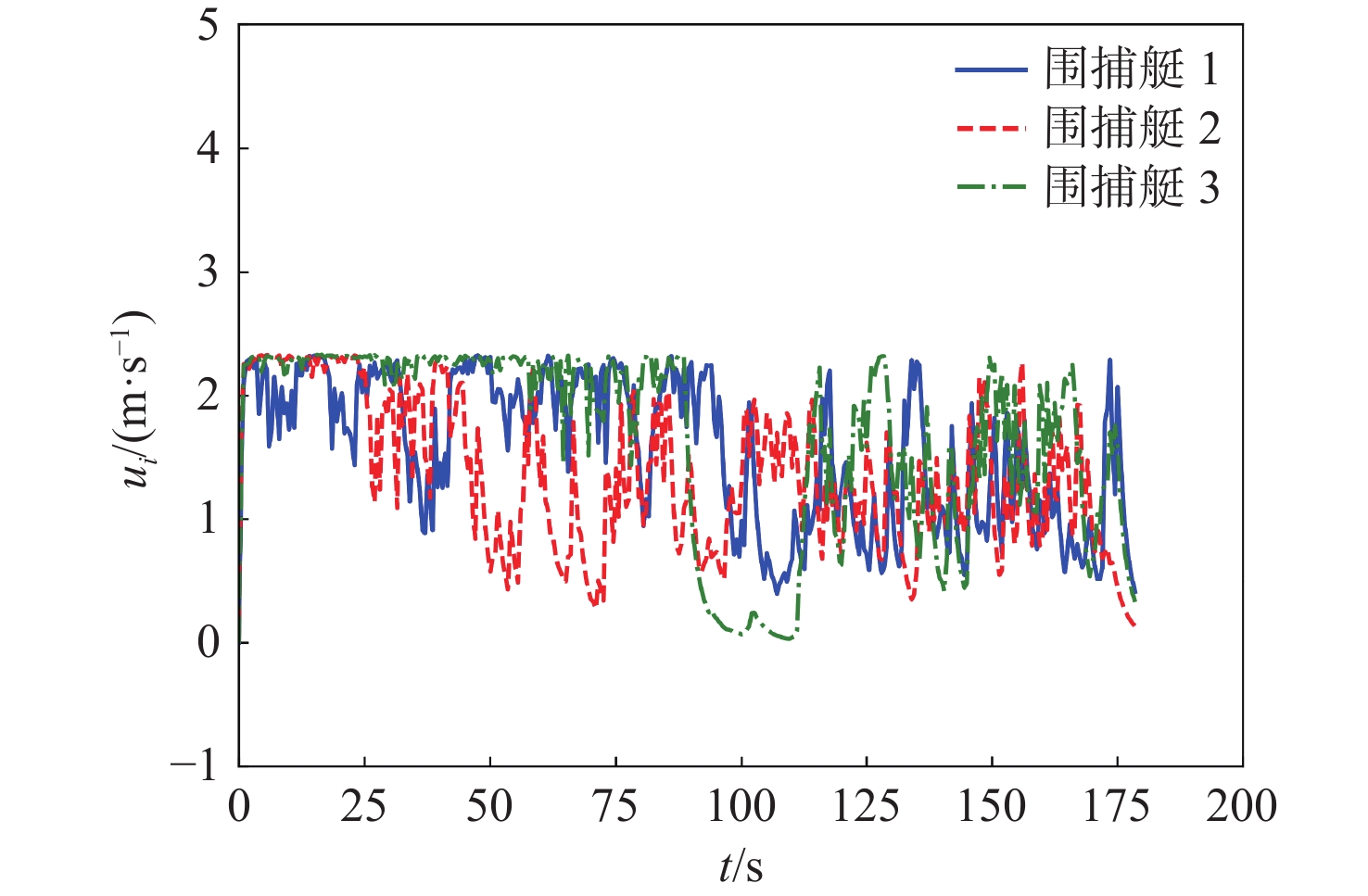
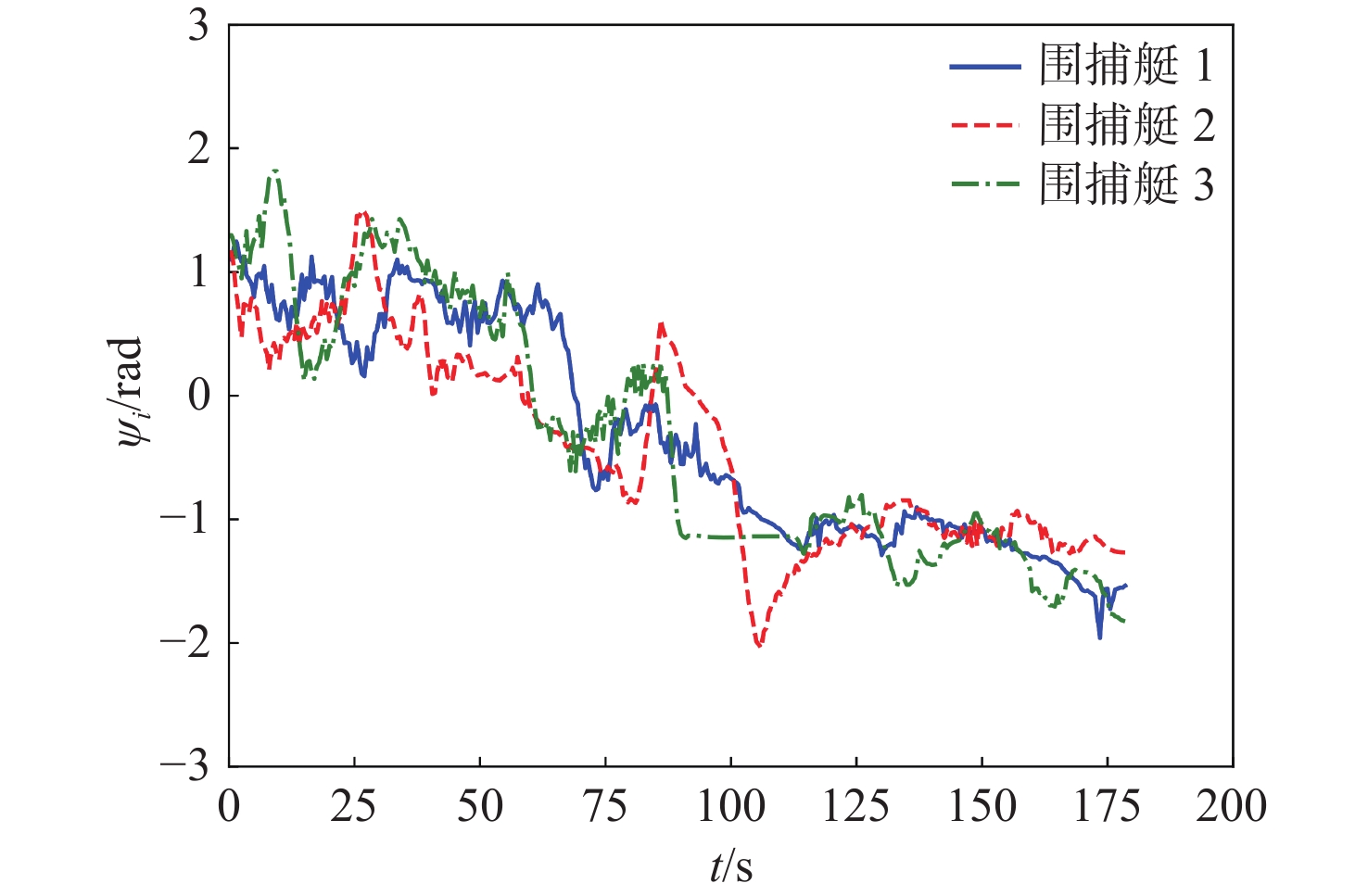
图11和图12分别给出各围捕艇的速度和航向角，可以看出，围捕艇从初始位置加速靠近目标，并不断调整自身的速度和角度，实现搜索、围困、捕获等行为。

图  11  各围捕艇的速度

Figure  11.  Velocities of hunting USVs

下载: 全尺寸图片 幻灯片

图  12  各围捕艇的航向角

Figure  12.  Heading angles of hunting USVs

下载: 全尺寸图片 幻灯片

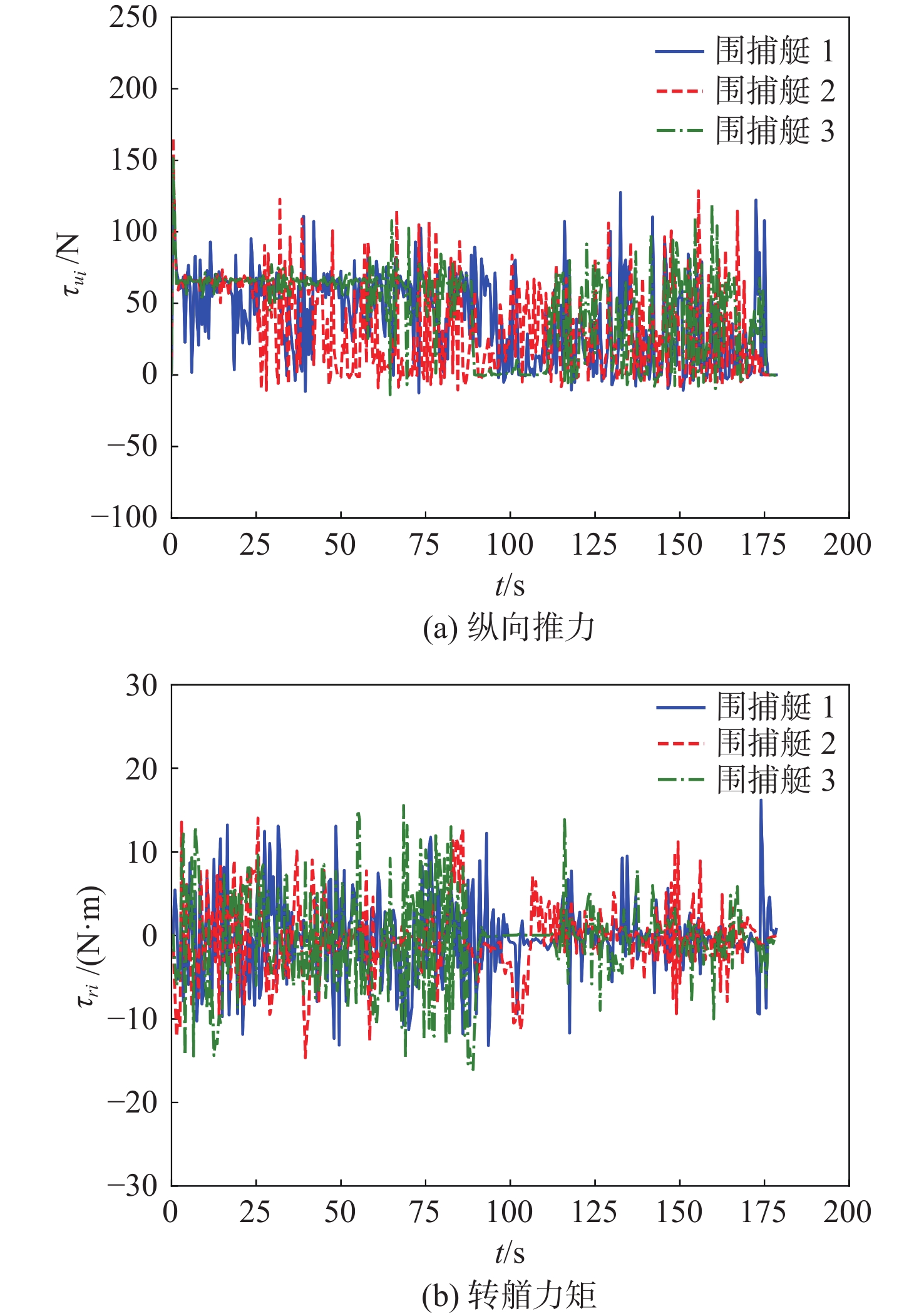
图13所示为系统控制输入，包括纵向推力和转艏力矩。可以看出，当围捕行为发生变化时，各围捕艇的控制输入会在奖励的约束下变化，以满足目标围捕需求。

图  13  各围捕艇的控制输入

Figure  13.  Control inputs of the hunting USVs

下载: 全尺寸图片 幻灯片

4.   结　语

考虑到现有多智能体强化学习的协同围捕成功率不高，本文提出一种基于阶段诱导学习的多无人艇协同目标围捕策略。首先，给出基于距离和角度的围捕成功判定条件，并据此将整个协同围捕过程划分为搜索、围困及捕获这３个阶段；接着，将LSTM引入Actor及Critic网络，搭建基于多智能体柔性行动−评判的协同目标围捕训练框架；最后，构建基于阶段诱导的协同围捕奖励机制，通过双方当前状态来优化训练进程，有效引导无人艇由易到难地实现目标围捕任务。基于三围一的仿真结果验证了该围捕策略的有效性。仿真对比结果表明，本文所提策略的围捕成功率相比MASAC+SI策略增加3.3%，MASAC+LSTM策略提升6.1%，相比MASAC策略提升24.4%。