基于Middlebrook的舰船电力电子化推进系统的稳定性分析和控制器参数优化方法

徐成虎; 李维波; 张浩; 彭智明; 方华亮

doi:10.19693/j.issn.1673-3185.03812

基于Middlebrook的舰船电力电子化推进系统的稳定性分析和控制器参数优化方法

徐成虎^1,,
李维波^{1, 2, ,},
张浩¹,
彭智明¹,
方华亮³

1.
武汉理工大学自动化学院，湖北武汉 430070
2.
西北民族大学电气工程学院，甘肃兰州 730124
3.
武汉大学电气与自动化学院，湖北武汉 430072

基金项目: 国家重点研发计划项目（2020YFB1506802）；国家自然科学基金面上项目（51977164）

详细信息

作者简介:
徐成虎，男，2000年生，硕士生。研究方向：电子信息。E-mail：3269180036@qq.com

李维波，男，1973年生，博士，教授，博士生导师。研究方向：电力电子技术在能源系统中的应用。E-mail：liweibo@whut.edu.cn

通讯作者:
李维波

中图分类号: U665.14
计量
- 文章访问数: 87
- HTML全文浏览量: 44
- PDF下载量: 20
出版历程
- 收稿日期: 2024-03-06
- 修回日期: 2024-03-25
- 网络出版日期: 2024-03-31

Stability analysis and controller parameter optimization method for ship power electronic propulsion system based on Middlebrook criterion

1.
School of Automation, Wuhan University of Technology, Wuhan 430070, China
2.
College of Electrical Engineering, Northwest Minzu University, Lanzhou 730124, China
3.
School of Electrical Engineering and Automation, Wuhan University, Wuhan 430070, China

基于Middlebrook的舰船电力电子化推进系统的稳定性分析和控制器参数优化方法徐成虎，采用知识共享署名4.0国际许可协议进行许可。

摘要

摘要:
目的
针对电力电子化装置占比严重的舰船直流推进系统的稳定性问题，提出基于Middlebrook的稳定性分析和控制器参数优化方法。
方法
首先，基于Middlebrook阻抗比稳定性判据，通过系统模型简化、非线性系统的线性化处理以及三相交流系统dq变换等，推演建立直流母线小信号输出阻抗、逆变器与电机的小信号输入阻抗模型；然后，通过粒子群算法优化控制器参数，在确保系统稳定的条件下最大限度地降低支撑电容取值；最后，搭建舰船直流推进系统仿真模型，开展支撑电容与直流母线的等效电阻和等效电感对系统稳定性影响的仿真分析。
结果
仿真结果表明：通过粒子群算法优化控制器参数之后，明显提高了系统稳定裕度，进而降低了支撑电容取值，这将有利于缩减舰船直流推进系统变流器整体尺寸。
结论
研究成果可为电力电子化占比严重的综合电力系统电压振荡及其抑制研究提供参考。
- 电力电子化装置 /
- 舰船直流推进 /
- 稳定性分析 /
- Middlebrook判据 /
- 小信号模型 /
- 支撑电容 /
- 粒子群算法
Abstract:
Objectives
Aiming at the stability problem of naval DC propulsion systems with a significant proportion of power electronic devices, a stability analysis and controller parameter optimization method based on the Middlebrook impedance ratio stability criterion is proposed.
Methods
First, the small-signal output impedance of the DC bus and small-signal input impedance of the inverter and motor are deduced and established through the simplification of the system model, linearization of the nonlinear system, dq transformation of the three-phase AC system, etc. The controller parameters are then optimized using a particle swarm algorithm to minimize the value of support capacitance on the condition of ensuring system stability. Finally, a simulation model of the DC propulsion system is constructed to simulate and analyze the influence of the support capacitance and equivalent resistance and inductance of the DC bus on the stability of the system.
Results
The simulation results show that the system's stability margin is obviously improved after the controller parameters are optimized by the particle swarm algorithm, which in turn lowers the value of support capacitance and reduces the overall size of the DC propulsion system's converter.
Conclusions
The findings of this study can provide useful references for research on voltage oscillations and their suppression in integr-ated power systems with a significant proportion of power electronic devices.
- power electronics device /
- ship DC propulsion /
- stability analysis /
- Middlebrook criterion /
- small signal model /
- support capacitor /
- particle swarm optimization

HTML全文

0. 引　言

从20世纪50年代开始，电力半导体技术得到了长足的发展，大量的电力电子器件在电力系统中得以应用，其中高压大容量电力电子器件在舰船电力系统中的应用尤为广泛^[1]。通过电力电子器件和计算机控制与通信技术集成一体的电力电子化装置，可以实现特定的电能转换功能^[2]，例如AC-DC变换器、DC-AC变换器和DC-DC变换器等，目前已大量列装于舰船直流推进系统、舰船直流组网系统等。研究表明，当电力电子化装置接入舰船直流推进系统之后，其闭环控制引起的负阻抗特性将削弱系统的阻尼效果，如果系统参数不匹配或受到外界干扰，极易导致系统不稳定，因此，有必要深入开展相关研究。

早期的船舶电力系统与动力系统相互独立，关联性不强^[3]；随着船舶电力系统和动力系统的多次改革发展，自80年代以来，船舶综合电力系统（integrated power system，IPS）应运而生，亦被称为船舶动力的第三次革命。该系统通过船舶综合电站为全船设备提供电能，实现了电力系统与动力系统的融合，从而提升了船舶性能和效率^[4]。

目前，针对电力系统的稳定性存在多种定义与分类，其中主流观点将稳定性分为小扰动下的静态稳定性和大扰动下的暂态稳定性^[5]：小扰动下的静态稳定性主要是指电力系统在受到微小扰动后，可以自我调整并回到原始的稳定状态的能力^[6]，即系统在小扰动下能够保持稳定；大扰动下的暂态稳定性是指在大扰动下可以迅速适应并恢复稳定，常用的静态稳定性分析方法包括频域阻抗分析法^[7]和特征值分析法^[8]。直流母线电压对电力变换装置的控制性能和系统运行的稳定性起着决定性作用，尤其对于船舶电力系统而言。为此，杨继沛等^[9]提出了一种新型的直流母线电压振荡抑制器，其采用有源电容作为关键组件，并与直流母线并联连接；该振荡抑制器可以直接与直流母线进行能量交互，并通过储能电容有效存储伴随电压振荡而产生的瞬变能量。该方案虽然可以降低电压振荡的幅值，但其电压振荡抑制器中的有源电容期望幅值需高于母线电压才能正常工作；否则，一旦母线发生故障，将极易造成过压而损坏IGBT器件。

鉴于直流母线电压对舰船直流推进系统的重要性，如何分析其稳定性就至关重要。早在上世纪70年代，美国加里福尼亚理工学院的Middlebrook教授提出了可用于判定级联直流变换器稳定性的Middlebrook判据^[10]，引入了复平面上的稳定禁区概念，该禁区要求最小环路增益的奈奎斯特曲线必须位于单位圆内，以确保交互系统的稳定性。Middlebrook方法为研究交互系统的阻抗稳定性奠定了基础，已成为行业内的标准方法；然而，该方法也存在一定的局限性，其无法直接求取非线性系统的阻抗模型，需首先对系统进行线性化处理。刘胜等^[11]利用Middlebrook判据，首先建立发电系统的非线性常微分方程模型来描述系统的动态行为，然后基于该模型来确定发电系统的小信号模型，进而通过小信号模型来分析系统特征值轨迹以评估发电系统的稳定性，最终解决了发电系统在恒功率负载下的电压不稳定问题，从而为发电系统的稳定性研究提供了一种有效工具。

电力电子化装置的控制器参数对系统稳定性的影响很大，因此，如何优化控制器参数来提升系统稳定性至关重要。Jiang等^[12]提出了一种有源阻尼控制器，并将其补充到电压源换流器（voltage source converter，VSC）的控制中，从而扩展了电流控制参数的稳定边界。VSC可以在更宽的参数选择范围内稳定运行，并在不削弱VSC动态控制能力的前提下有效抑制振荡。该方法通过新增一种有源阻尼控制器而扩展了电流控制参数的稳定边界，但同时也扩大了系统的整体成本。储天舒等^[13]提出了一种基于子空间模型的控制器参数优化方法，虽然可以得到最优的控制器参数，但算法复杂、计算量大，难以实现工程应用。

为此，本文拟针对舰船直流推进系统接入电力电子化装置后的稳定性问题，利用Middlebrook稳定性判据开展研究，考虑应用对象的局限性和本文研究对象的复杂程度，通过假定恒功率负载简化系统模型、求取传递函数及线性化处理，以建立小信号输入/输出阻抗模型，进而分析影响该系统稳定性的关键性参数及其对稳定性的影响规律；在此基础上，将通过粒子群算法来优化电流控制器的参数，从而在确保系统稳定的条件下降低支撑电容取值，以有效缩减舰船直流推进系统的总体尺寸。

1. 电力电子化舰船的直流推进系统模型

1.1 舰船直流推进系统的总体架构

以某型舰船直流推进系统为例，其总体架构如图1所示，发电机组输出的三相交流电经24脉波不控整流装置滤波之后输送给直流母线（DC-link），直流母线电压经过逆变器装置转换为交流电之后供给推进电机。由此可见，直流母线电压借助其他的电力电子化变换装置，可以转换为不同等级的交流电或直流电，进而供给相应负载。

图 1 舰船直流推进系统的总体架构

Figure 1. Topology of ship DC propulsion system

下载: 全尺寸图片幻灯片

1.2 系统简化模型

电力变换装置通常采用反馈输出电压、电流、功率等方式实现闭环控制，从而满足系统的控制需求。在控制器响应速度足够快和不考虑功率损耗的条件下，电力变换装置的瞬时输入功率保持不变，因此可以将其视为恒功率负载^[14]，这意味着无论输入电压如何波动，电力变换装置都将自适应地调整输出电流和电压，以保持恒定的输入功率。

恒功率负载的小信号输入阻抗 ${Z_{{\text{cpl}}}}$ 恒小于零，其绝对值等于负载稳态工况下的等效阻抗，该特性即为恒功率负载的负阻抗特性^[15]，其表达式为

$\left| {{Z_{{\text{cpl}}}}} \right| = \left| { - \dfrac{{{{(U_{{\text{dc}}}^{\text{0}})}^2}}}{{P_{{\text{cpl}}}^{\text{0}}}}} \right|$

(1)

式中， $U_{{\text{dc}}}^{\text{0}}$ ， $P_{{\text{cpl}}}^{\text{0}}$ 分别为系统稳态运行工况下的直流母线侧输出电压以及负载功率。

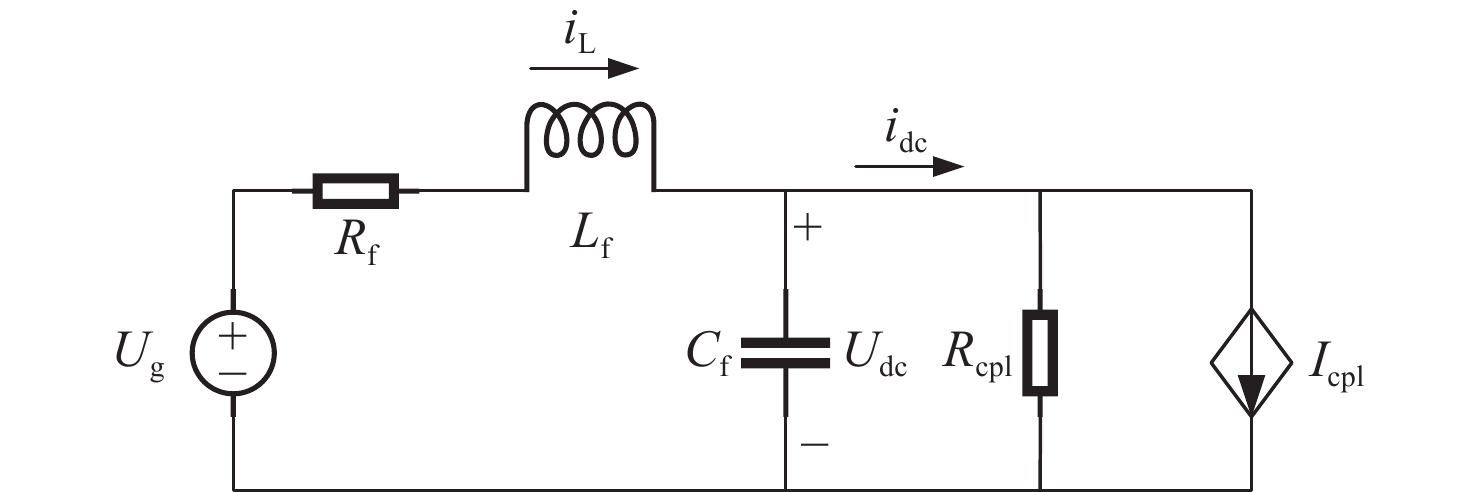
为了便于分析直流母线电压的稳定性，一般将交流源和整流器整体简化为一个由理想直流源、电感、电容和电阻组成的联合电路；由于恒功率负载具有负阻抗特性，因此可以将逆变器–电机整体简化为一个由负电阻R_cpl和恒流源I_cpl组成的并联系统。通过这样的简化，即可得到如图2所示的舰船直流推进系统的简化模型，其中：U_g为理想的直流源电压；U_dc为直流母线电压（DC-link）；R_f，C_f，L_f分别为直流母线的电阻、电容和电感；i_L为电感电流；i_dc为直流母线电流。

图 2 舰船直流推进系统的简化模型

Figure 2. Simplified model of ship DC propulsion system

下载: 全尺寸图片幻灯片

2. 电力电子化舰船直流推进系统的稳定性机理分析

2.1 直流母线的振荡机理分析

现有研究表明，当舰船直流推进系统接入电力电子化装置之后，其系统稳定性必将受到明显影响。作为链接枢纽，直流母线是否振荡失稳非常关键，因此，有必要开展直流母线的振荡机理研究^[16]。

根据图2的简化模型和基尔霍夫定律，直流源电压U_g和电感电流i_L为

$\left\{ \begin{aligned} & {{U_{\text{g}}} = {R_{\text{f}}}{i_{\text{L}}} + {L_{\text{f}}}\dfrac{{{\text{d}}{i_{\text{L}}}}}{{{\text{d}}t}} + {U_{{\text{dc}}}}} \\ & {{i_{\text{L}}} = {C_{\text{f}}}\dfrac{{{\text{d}}{U_{{\text{dc}}}}}}{{{\text{d}}t}} + \dfrac{{{U_{{\text{dc}}}}}}{{{R_{{\text{cpl}}}}}}} \end{aligned} \right.$

(2)

式中，t为时间变量。将式(1)进行拉氏变换，则系统的传递函数为

$\dfrac{{{U_{{\text{dc}}}}(s)}}{{{U_{\text{g}}}(s)}} = \dfrac{1}{{{L_{\text{f}}}{C_{\text{f}}}{s^2} + \left({R_{\text{f}}}{C_{\text{f}}} + \dfrac{{{L_{\text{f}}}}}{{{R_{{\text{cpl}}}}}}\right)s + \left(1 + \dfrac{{{R_{\text{f}}}}}{{{R_{{\text{cpl}}}}}}\right)}}$

(3)

式中，U_dc(s) ，U_g(s)分别为直流母线电压、直流源电压的拉氏变换，其中s为复变量。

系统的特征方程λ(s)为

$\lambda (s) = {s^2} + \left(\dfrac{{{R_{\text{f}}}}}{{{L_{\text{f}}}}} + \dfrac{1}{{{C_{\text{f}}}{R_{{\text{cpl}}}}}}\right)s + \left(\dfrac{1}{{{L_{\text{f}}}{C_{\text{f}}}}} + \dfrac{{{R_{\text{f}}}}}{{{L_{\text{f}}}{C_{\text{f}}}{R_{{\text{cpl}}}}}}\right) = 0$

(4)

采用小信号分析恒功率负载时，其输入阻抗Z_cpl必须满足如下条件：

$\left| {{Z_{{\text{cpl}}}}} \right| = \left| { - \dfrac{{{{(U_{{\text{dc}}}^{\text{0}})}^2}}}{{P_{{\text{cpl}}}^{\text{0}}}}} \right| > > {R_{\text{f}}}$

(5)

对于直流推进系统而言，为简化分析，假设Z_cpl≈R_cpl，则式（4）可以改写为

$\lambda (s) = {s^2} + \left(\dfrac{{{R_{\text{f}}}}}{{{L_{\text{f}}}}} - \dfrac{{{P_{{\text{cpl}}}}}}{{{C_{\text{f}}}U_{{\text{dc}}}^2}}\right)s + \left(\dfrac{1}{{{L_{\text{f}}}{C_{\text{f}}}}} - \dfrac{{{P_{{\text{cpl}}}}{R_{\text{f}}}}}{{{L_{\text{f}}}{C_{\text{f}}}U_{{\text{dc}}}^2}}\right) = 0$

(6)

式中， ${P_{{\text{cpl}}}}$ 为负载功率。

根据劳斯判据^[17]可知，系统稳定的条件是其特征方程的根存在负实部，即式(4)特征方程的常数项恒大于0，则系统稳定的判据为

${P_{{\text{cpl\_H}}}} < \dfrac{{{R_{\text{f}}}{C_{\text{f}}}U_{{\text{dc\_H}}}^2}}{{{L_{\text{f}}}}}$

(7)

式中，P_{cpl_H}，U_{dc_H}分别为稳定条件下的临界负载功率和临界母线电压。

综上所述，推进系统的稳定性与直流母线电路参数、负载功率均密切相关，在既定设计参数条件下，推进系统负载功率都存在一个上限值P_limit；否则，当运行功率超过上限值P_limit时，直流母线电压极易发生振荡失稳，进而影响系统运行的可靠性。

2.2 Middlebrook稳定性分析方法

2.2.1 Middlebrook阻抗比判据分析

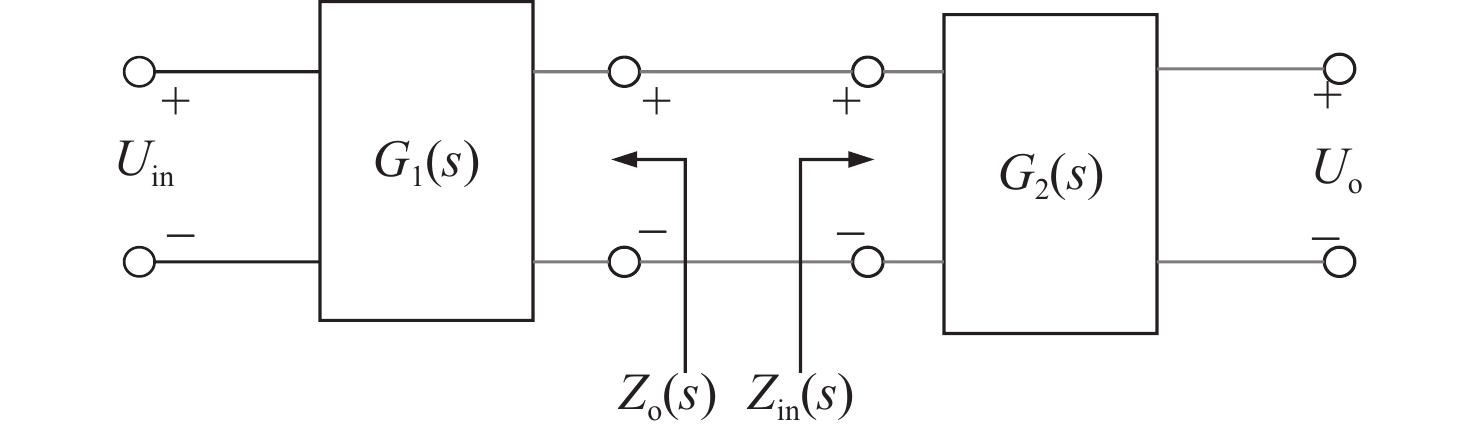
上世纪70年代中期，Middlebrook教授针对分布式电源系统级联直流变换器和滤波器的稳定性问题，提出了基于阻抗的分析方法。舰船直流推进系统与分布式电源系统在拓扑架构上具有一定的相似性，故可借鉴分布式电源系统的分析方法。图3所示为直流变换器和滤波器级联系统的等效模型，其中：U_in，U_o分别为输入电压、输出电压；G₁(s)，G₂(s)分别为前级、后级变换器的传递函数；Z_o(s)，Z_in(s)分别为前级变换器的输出阻抗和后级变换器的输入阻抗。

图 3 级联系统的等效模型

Figure 3. Equivalent model of cascade system

下载: 全尺寸图片幻灯片

级联系统的传递函数F(s)为

$F(s) = \dfrac{{{G_1}(s){G_2}(s)}}{{1 + {Z_{\text{o}}}(s)/{Z_{{\text{in}}}}(s)}} = \dfrac{{{G_1}(s){G_2}(s)}}{{1 + {T_{\text{m}}}(s)}}$

(8)

${T_{\text{m}}}(s) = {Z_{\text{o}}}(s)/{Z_{{\text{in}}}}(s)$

(9)

式中，T_m(s)为等效环路增益。

Middlebrook方法指出，根据等效环路增益T_m(s)是否满足奈奎斯特判据，即可判断系统的稳定性。图4所示为等效环路增益T_m(s)的奈奎斯特曲线，其中实线内部为系统稳定时的T_m(s)奈奎斯特曲线，虚线部分则为T_m(s)禁止区。由图4得知，如果系统稳定，则等效环路增益T_m(s)的奈奎斯特曲线不包围（−1，j0）点，并可根据奈奎斯特曲线与（−1，j0）点的靠近程度来判断系统的相对稳定程度。根据Middlebrook方法，如果保证全频率范围内前级变换器的输出阻抗幅值远小于后级变换器的输入阻抗幅值，即可实现系统稳定。

图 4 T_m(s)的奈奎斯特曲线

Figure 4. Nyquist curve of T_m(s)

下载: 全尺寸图片幻灯片

2.2.2 直流母线侧的输出阻抗模型分析

对于图1所示的拓扑结构，基于小信号分析方法可以得到直流母线侧输出阻抗Z_o(s)与导纳Y_o(s)的关系为

${Z_{\text{o}}}(s) = 1/{Y_{\text{o}}}(s) = \dfrac{{{L_{\text{f}}}s + {R_{\text{f}}}}}{{{L_{\text{f}}}{C_{\text{f}}}{s^2} + {R_{\text{f}}}{C_{\text{f}}}s + 1}}$

(10)

因此，谐振频率f_r可以表示为

${f_{\text{r}}} = \dfrac{1}{{2{\text{π }}\sqrt {{L_{\text{f}}}{C_{\text{f}}}} }}$

(11)

2.2.3 推进电机阻抗的模型分析

永磁同步电机（permanent magnet synchronous motor，PMSM）存在多种数学建模方法，不同模型对控制性能好坏、控制难易程度的影响较大。由于PMSM是一个高阶的非线性系统^[18]，因此，建立一个兼顾控制性能和控制难易程度的数学模型至关重要，相关研究表明，建立d-q坐标系下的PMSM数学模型最为合适。为简化分析，作出如下假设：

1）忽略铁芯的磁路饱和及高次谐波；

2）忽略电机中的涡流和磁滞损耗；

3）输入电流为三相对称正弦波电流，定子绕组在空间上三相对称。

根据坐标变换和矢量控制理论，得出如图5所示的逆变器–电机系统及其控制框图，其中：ω_m^*，ω_m分别为电机角速度的设定值和实际值；PI为比例积分（proportional integral）控制方法；θ为定子与转子之间的夹角； i_q^*，i_q分别为q轴的参考电流和实际电流；i_d^*，i_d分别为d轴的参考电流和实际电流；U_q^*，U_d^*分别为q轴和d轴的参考电压；U_α，U_β分别为α轴和β轴的电压；2r/2s，3s/3r分别为反Park变换，Clark变换与Park变换；SVPWM为空间矢量脉宽调制（space vector pulse width modulation）；i_A，i_B，i_C为A，B，C三相电流。

图 5 逆变器–电机系统及其控制框图

Figure 5. Inverter motor system and its control block diagram

下载: 全尺寸图片幻灯片

PMSM的运动方程为

$\left( {Js + \beta } \right){\omega _{\text{m}}} = 1.5{P_{\text{n}}}\left( {{\psi _{\text{f}}}{i_{\text{q}}} + \left( {{L_{\text{d}}} - {L_{\text{q}}}} \right){i_{\text{d}}}{i_{\text{q}}}} \right) - {T_{\text{L}}}$

(12)

式中：J为电机转动惯量；β为黏性摩擦常数；P_n为磁极对数；ψ_f为永磁体磁链；i_d，i_q，L_d，L_q分别为同步旋转坐标系d，q轴上的电机定子电流和电感；T_L为负载转矩。

在两相同步旋转坐标系下，PMSM的d轴电压u_d和q轴电压u_q分别为

$\left\{ \begin{aligned} & {{u_{\text{d}}} = ({R_{\text{s}}} + s{L_{\text{d}}}){i_{\text{d}}} - {P_{\text{n}}}{\omega _{\text{m}}}{L_{\text{q}}}{i_{\text{q}}}} \\ & {{u_{\text{q}}} = ({R_{\text{s}}} + s{L_{\text{q}}}){i_{\text{q}}} + {P_{\text{n}}}{\omega _{\text{m}}}({L_{\text{d}}}{i_{\text{d}}} + {\psi _{\text{f}}})} \end{aligned}\right.$

(13)

式中，R_s为定子电阻。

假设不考虑损耗，则逆变器直流侧输入功率与交流侧输出功率相等，即

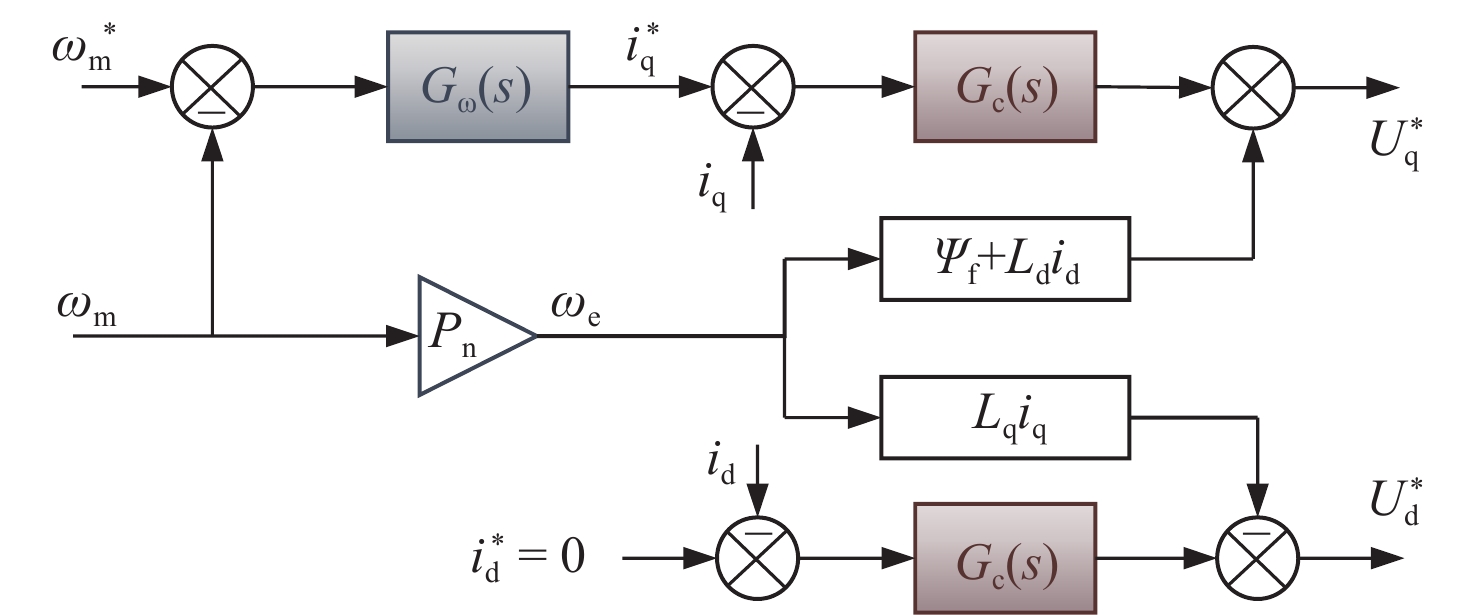
${U_{{\text{dc}}}}{i_{{\text{dc}}}} = \dfrac{3}{2}({u_{\text{d}}}{i_{\text{d}}} + {u_{\text{q}}}{i_{\text{q}}})$

(14)

PMSM采用常规的转速、电流双闭环控制，且转速环和电流环均采用PI控制方法，其矢量控制框图详见图6，其中：G_ω(s)，G_c(s)分别为PMSM的转速控制器的传递函数和电流控制器的传递函数；ω_e为电机的电角速度。

图 6 PMSM矢量控制框图

Figure 6. Vector control block diagram of PMSM

下载: 全尺寸图片幻灯片

$\left\{ \begin{aligned} & {{G_\omega }(s) = {k_{\omega {\text{p}}}} + \dfrac{{{k_{\omega {\text{i}}}}}}{s}} \\ & {{G_{\text{c}}}(s) = {k_{I{\text{p}}}} + \dfrac{{{k_{I{\text{i}}}}}}{s}} \end{aligned} \right.$

(15)

式中：k_ωp和k_ωi分别为转速控制器的比例和积分系数；k_Ip和k_Ii分别为电流控制器的比例和积分系数。

因此，PMSM的转速控制器输出的q轴参考电流i^*_q为

$i_{\text{q}}^* = {G_\omega }(s)(\omega _{\text{m}}^* - {\omega _{\text{m}}})$

(16)

PMSM的电流控制器输出的q轴以及d轴的参考电压U^*_q和U^*_d分别为

$\left\{ \begin{aligned} & {U_{\text{q}}^* = {G_{\text{c}}}(s)(i_{\text{q}}^* - {i_{\text{q}}}) + {P_{\text{n}}}{\omega _{\text{m}}}({\psi _{\text{f}}} + {L_{\text{d}}}{i_{\text{d}}})} \\ & {U_{\text{d}}^* = {G_{\text{c}}}(s)(i_{\text{d}}^* - {i_{\text{d}}}) - {P_{\text{n}}}{\omega _{\text{m}}}{L_{\text{q}}}{i_{\text{q}}}} \end{aligned}\right.$

(17)

在稳态运行工况下，可以认为负载转矩波动ΔT_L=0，黏性摩擦常数β≈0，以及d轴上的电机定子电流波动Δi_d=0，由此分别对式(12)、式(13)和式(17)进行小信号线性化处理，得

$\Delta {\omega _{\text{m}}}Js = 1.5{P_{\text{n}}}{\psi _{\text{f}}}\Delta {i_{\text{q}}}$

(18)

$\Delta {u_{\text{q}}} = ({R_{\text{s}}} + s{L_{\text{q}}})\Delta {i_{\text{q}}} + {P_{\text{n}}}{\psi _{\text{f}}}\Delta {\omega _{\text{m}}}$

(19)

$\Delta {u_{\text{q}}} = (u_{\text{q}}^0/U_{{\text{dc}}}^0)\Delta {U_{{\text{dc}}}}$

(20)

$U_{{\text{dc}}}^0\Delta {i_{{\text{dc}}}} + i_{{\text{dc}}}^0\Delta {U_{{\text{dc}}}} = 1.5(i_{\text{q}}^0\Delta {u_{\text{q}}} + u_{\text{q}}^0\Delta {i_{\text{q}}})$

(21)

${G_{\text{c}}}(s)\Delta {i_{\text{q}}} = {P_{\text{n}}}{\psi _{\text{f}}}\Delta {\omega _{\text{m}}}$

(22)

以上式中：Δ(·)表示 (·)的波动值；上角标“0”表示稳态值。

联立式(19)、式(20)和式(22)，得

$\dfrac{{\Delta {i_{\text{q}}}}}{{\Delta {U_{{\text{dc}}}}}} = \dfrac{{(u_{\text{q}}^0/U_{{\text{dc}}}^0)}}{{{R_{\text{s}}} + s{L_{\text{q}}} + {G_{\text{c}}}(s)}}$

(23)

联立式(21)和式(23)，可得逆变器−电机系统输入阻抗Z_in(s)及其导纳Y_in(s)之间的关系式，即

$\begin{split} & \qquad\qquad {Y_{{\text{in}}}}(s) = 1/{Z_{{\text{in}}}}(s) = \dfrac{{\Delta {i_{{\text{dc}}}}}}{{\Delta {U_{{\text{dc}}}}}} = \\& \dfrac{{1.5(u_{\text{q}}^0/U_{{\text{dc}}}^0)}}{{U_{{\text{dc}}}^0}}\dfrac{{\left( {u_{\text{q}}^0 + i_{\text{q}}^0({R_{\text{s}}} + s{L_{\text{q}}} + 1.5P_{\text{n}}^2\psi _{\text{f}}^2/(Js))} \right)}}{{{R_{\text{s}}} + s{L_{\text{q}}} + {G_{\text{c}}}(s)}} - \dfrac{{i_{{\text{dc}}}^0}}{{U_{{\text{dc}}}^0}} \end{split}$

(24)

3. 推进系统的稳定性分析

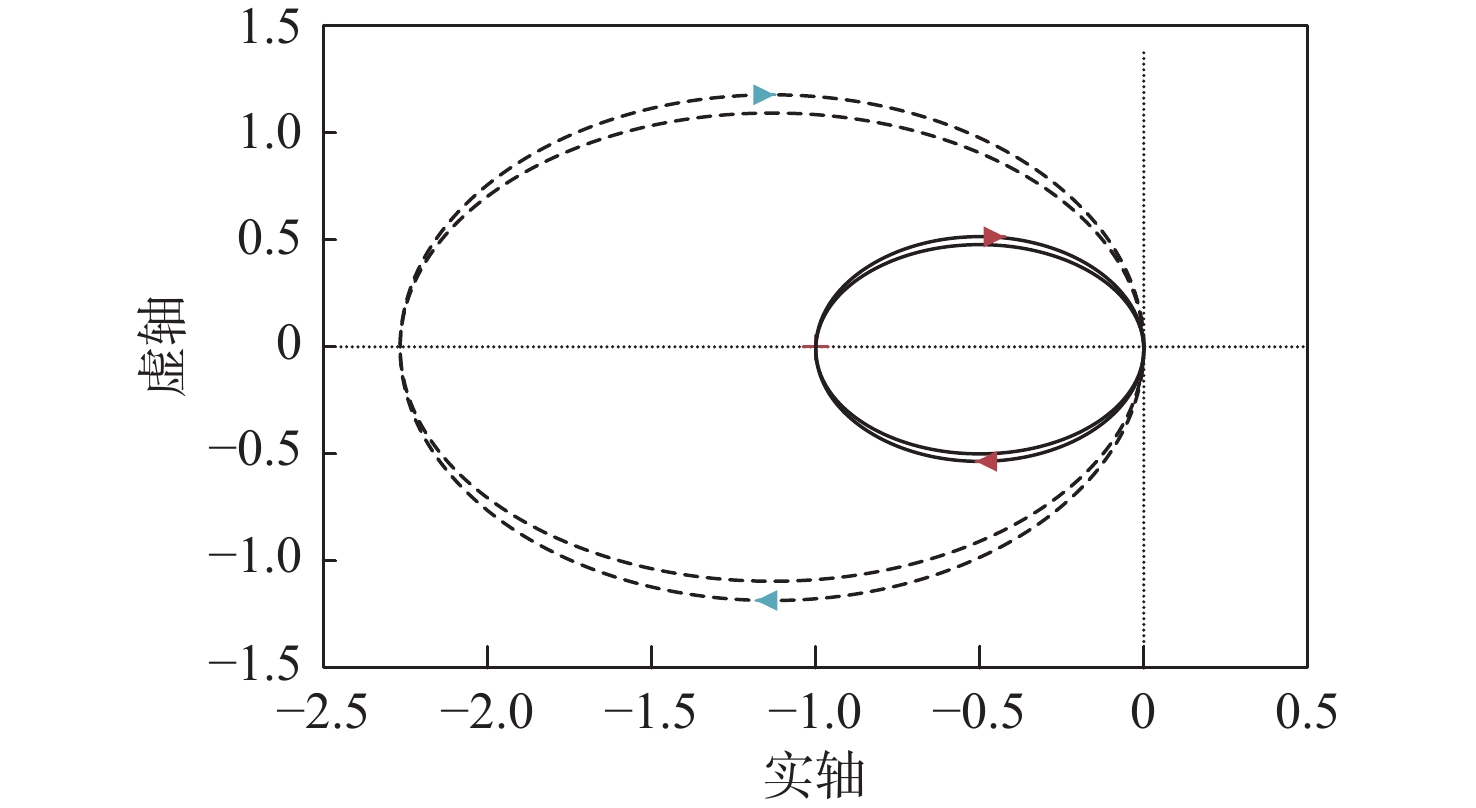
根据Middlebrook阻抗比判据，利用推导获得的阻抗/导纳模型，即可对船舶直流电力推进系统直流母线的稳定性问题开展仿真研究，其关键性仿真参数如表1所示。在此基础上，结合阻抗/导纳模型，即可绘制图7所示的T_m(s)=Y_in(s)/Y_o(s)的奈奎斯特图。随着直流母线电容C_f的减小，等效环路增益T_m(s)的奈奎斯特曲线从不包含（−1，j0）变为逐渐包含（−1，j0）。根据Middlebrook阻抗比判据，随着直流母线电容C_f的减小，推进系统将逐渐失稳，这与上文直流母线振荡机理的分析结论一致。

表 1 关键性仿真参数

Table 1. Key simulation parameters

参数	数值	参数	数值
母线电容C_f/mF	10	定子电阻R_s/mΩ	1.502
母线电感L_f/mH	0.2	电感L_d，L_q/mH	0.476 7
母线电阻R_f/mΩ	1	磁极对数P_n	8
母线电压U_dc/V	1 200	永磁体磁链ψ_f/Wb	3.55
负载转矩T_L/(N·m)	195 200	转动惯量J/(kg·m²)	550
转速控制器的比例系数k_ωp	50	电流控制器的比例系数k_Ip	40
转速控制器的积分系数k_ωi	0.2	电流控制器的积分系数k_Ii	0.1

下载: 导出CSV

| 显示表格

图 7 随着C_f变化的T_m(s)奈奎斯特图

Figure 7. Nyquist plot of T_m(s) as C_f changes

下载: 全尺寸图片幻灯片

进一步，其他参数保持不变，仅改变直流母线电感L_f的大小，即可绘制出T_m(s)随L_f变化的奈奎斯特图，如图8所示。随着直流母线电感L_f的增加，T_m(s)的奈奎斯特曲线从不包含（−1，j0）变为逐渐包含（−1，j0）。根据Middlebrook阻抗比判据，随着直流母线电感L_f的增加，推进系统将逐渐失稳，这也与上文直流母线振荡机理的分析结论一致。

图 8 随着L_f变化的T_m(s)奈奎斯特图

Figure 8. Nyquist plot of T_m(s) as L_f changes

下载: 全尺寸图片幻灯片

进一步，保持其他参数不变，仅仅改变直流母线电阻R_f的大小，绘制出T_m(s)随R_f变化的奈奎斯特图，如图9所示。随着直流母线电阻R_f的减小，T_m(s)的奈奎斯特曲线从不包含（−1，j0）变为逐渐包含（−1，j0）。根据Middlebrook阻抗比判据，随着直流母线电阻R_f的减小，推进系统将逐渐失稳，这也与上文直流母线振荡机理的分析结论一致。

图 9 随着R_f变化的T_m(s)奈奎斯特图

Figure 9. Nyquist plot of T_m(s) as R_f changes

下载: 全尺寸图片幻灯片

对比分析图7～图9的仿真结果可知，当负载保持恒定功率时，直流母线电容C_f、电阻R_f和电感L_f的变化，均将直接影响直流母线的稳定性，进而影响整个推进系统的稳定性。对于舰船推进系统而言，在设计建造完成之后难以改变直流母线的等效电阻和等效电感，但可以改变支撑电容，这为推进系统的稳定性调节提供了便利条件。因此，如何在保证推进系统稳定的前提下，通过优化控制器参数来减小支撑电容取值，对于有效降低推进系统的变流器总体尺寸而言是一个有重要价值的研究问题。

4. 粒子群算法优化控制器参数

分析式(24)可知，逆变器−电机系统的输入阻抗与电流控制器G_c(s)的参数k_Ip和k_Ii有关，可以进一步认为系统稳定性与参数k_Ip，k_Ii有关，因此，通过优化参数k_Ip，k_Ii可以提高母线电压的抗振荡能力，进而减小直流母线支撑电容取值，并减小变流器尺寸。

4.1 粒子群优化算法

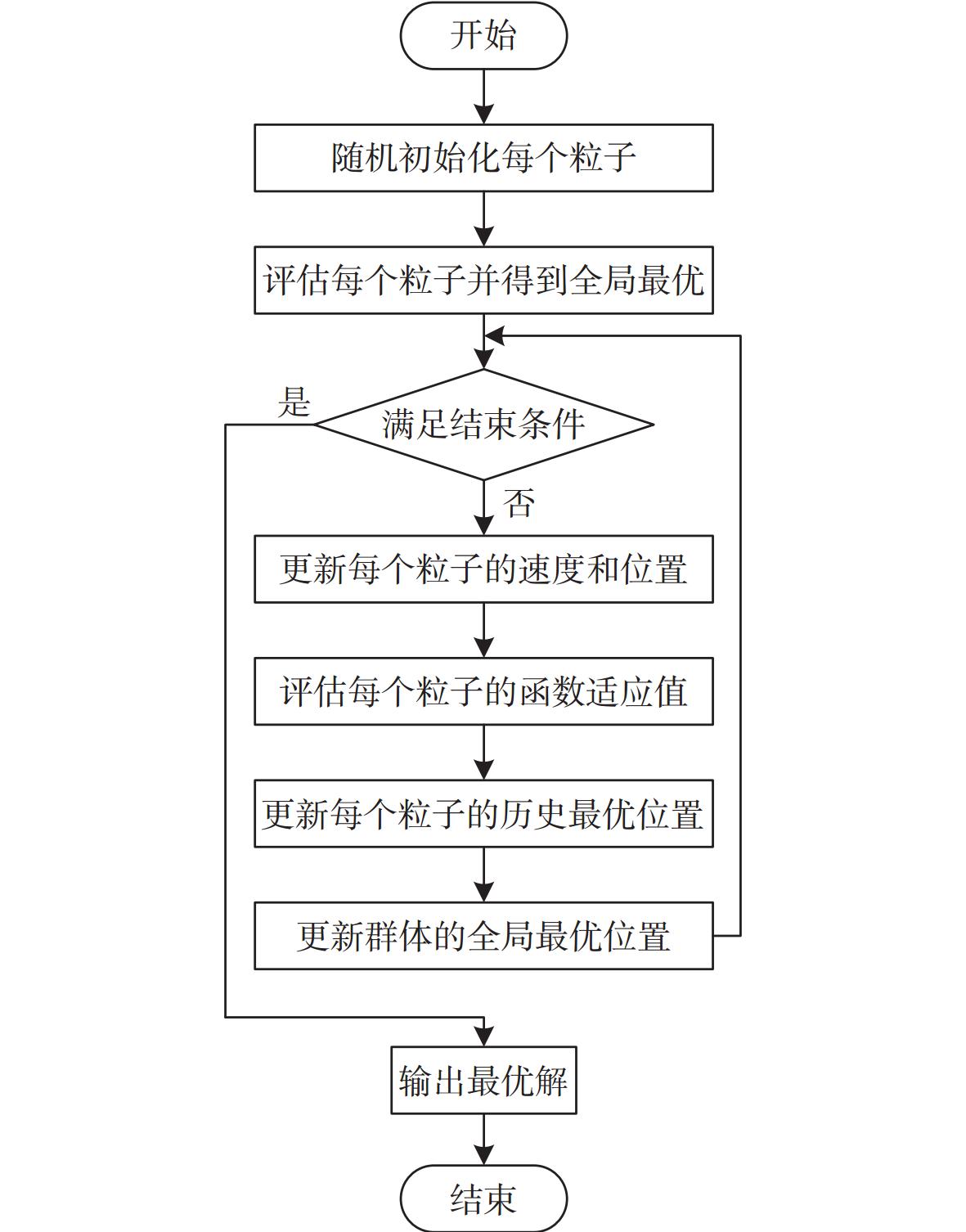
粒子群优化算法（particle swarm optimization，PSO）是一种进化计算技术，常用于参数优化。粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，其粒子仅具有2个属性：速度和位置，速度代表移动的快慢，位置则代表移动的方向。每个粒子在搜索空间中单独地搜寻最优解，将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的个体极值即作为整个粒子群的当前全局最优解，粒子群中的所有粒子可以根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。粒子群算法的流程相对比较简单，主要分为：1）初始化粒子群；2）评价粒子，即计算适应值；3）寻找个体极值；4）寻找全局最优解；5）修改粒子的速度和位置，如图10所示。

图 10 粒子群算法的流程图

Figure 10. The flowchart of particle swarm optimization algorithm

下载: 全尺寸图片幻灯片

4.2 粒子群算法优化目标函数

为减小支撑电容取值，需提高系统的稳定性，所以应使特征值均在左半平面，且其实部的绝对值应较大，则支撑电容的优化目标函数为

$F = {\omega _1}[{\text{Re}}(\lambda )] + {\omega _2}{C_{\text{f}}}$

(25)

式中：F为稳定裕度；ω₁>0，为系统特征值的实部所在项的权重；Re(λ)为主导极点的实部，其中λ为主导极点；ω₂<1，为支撑电容所在项的权值。

本文需确保系统的稳定性，即特征值的实部应小于0，因此各指标的权重排序为ω₂>ω₁，本文取值为ω₁=0.4，ω₂=0.6。

4.3 粒子群算法优化参数

为保证系统的稳定性，本节将对电流控制器G_c(s)的参数k_Ip，k_Ii进行优化，进而为参数赋予一个取值范围，即参数的稳定域。根据Middlebrook阻抗比判据，利用推导获得的阻抗/导纳模型，即可求得k_Ip，k_Ii的稳定域分别为[1，50] 和[0.01，1]。

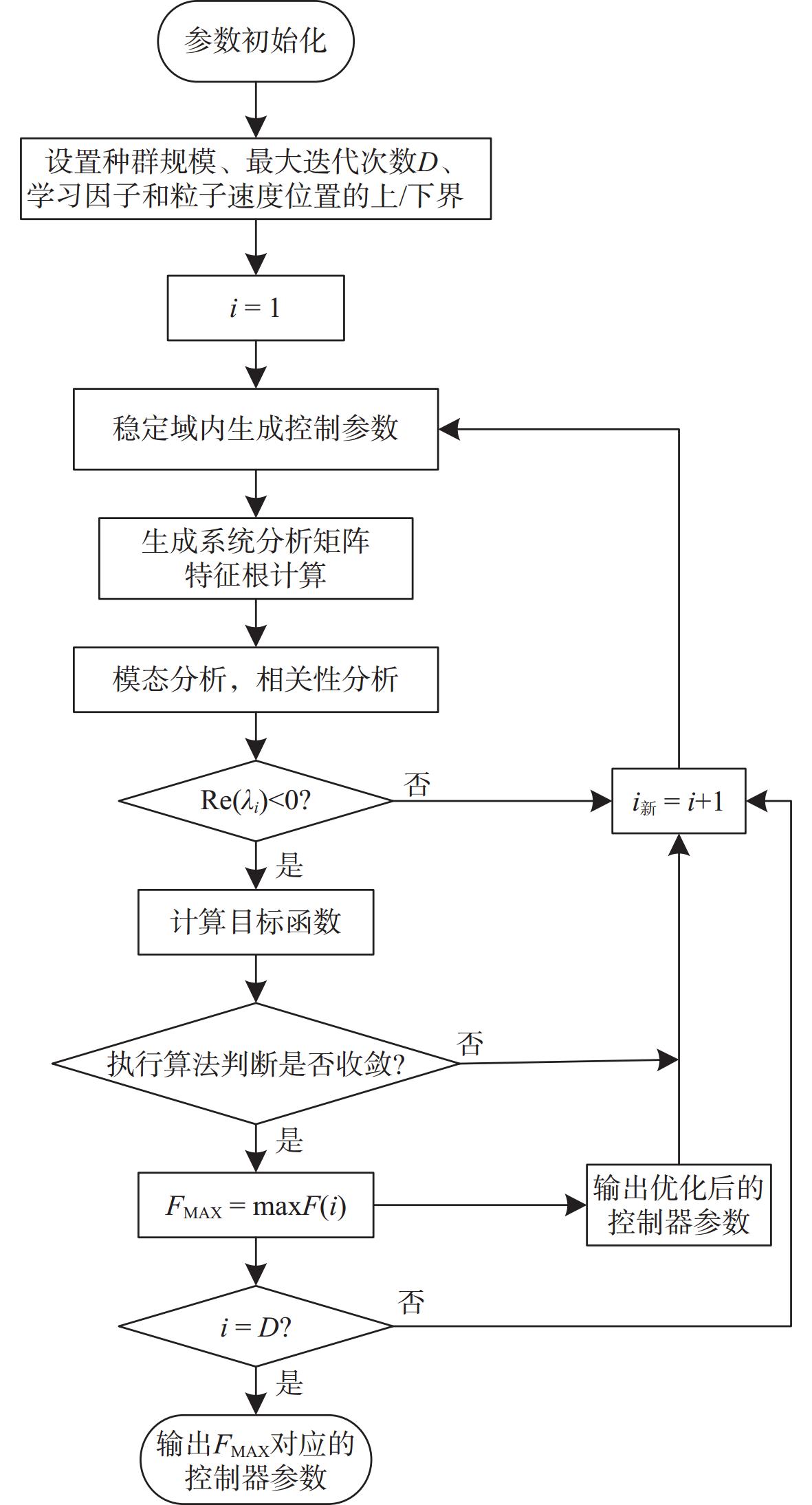
图11所示为参数优化流程：首先，在循环开始前进行参数初始化，设置种群规模、最大迭代次数D（i=1，2，…，D）、学习因子和粒子速度、位置的上限和下限；然后，在稳定域内随机生成控制器参数k_Ip，k_Ii的值，进而对系统特征值进行稳定性判断，如果稳定则计算稳定裕度F(i)，并记录控制器参数和F(i)的值，反之则需重复迭代计算；最后，依据粒子群算法寻找F的最大值F_MAX，并输出对应的控制器参数值。

图 11 参数优化的流程图

Figure 11. Flowchart for parameter optimization

下载: 全尺寸图片幻灯片

粒子群算法优化后的结果如图12所示。选取F最大时的控制器参数k_Ip=31.25，k_Ii=0.26，代入T_m(s)=Y_in(s)/Y_o(s)中，即可得到系统在临界稳定状态下的C_f值。

图 12 参数优化的结果

Figure 12. Result graph for parameter optimization

下载: 全尺寸图片幻灯片

优化前后的参数取值如表2所示，可以看出，当优化参数之后，采用较小的支撑电容即可令母线电压达到稳定，这对于降低舰船直流推进系统的变流器尺寸而言意义重大。

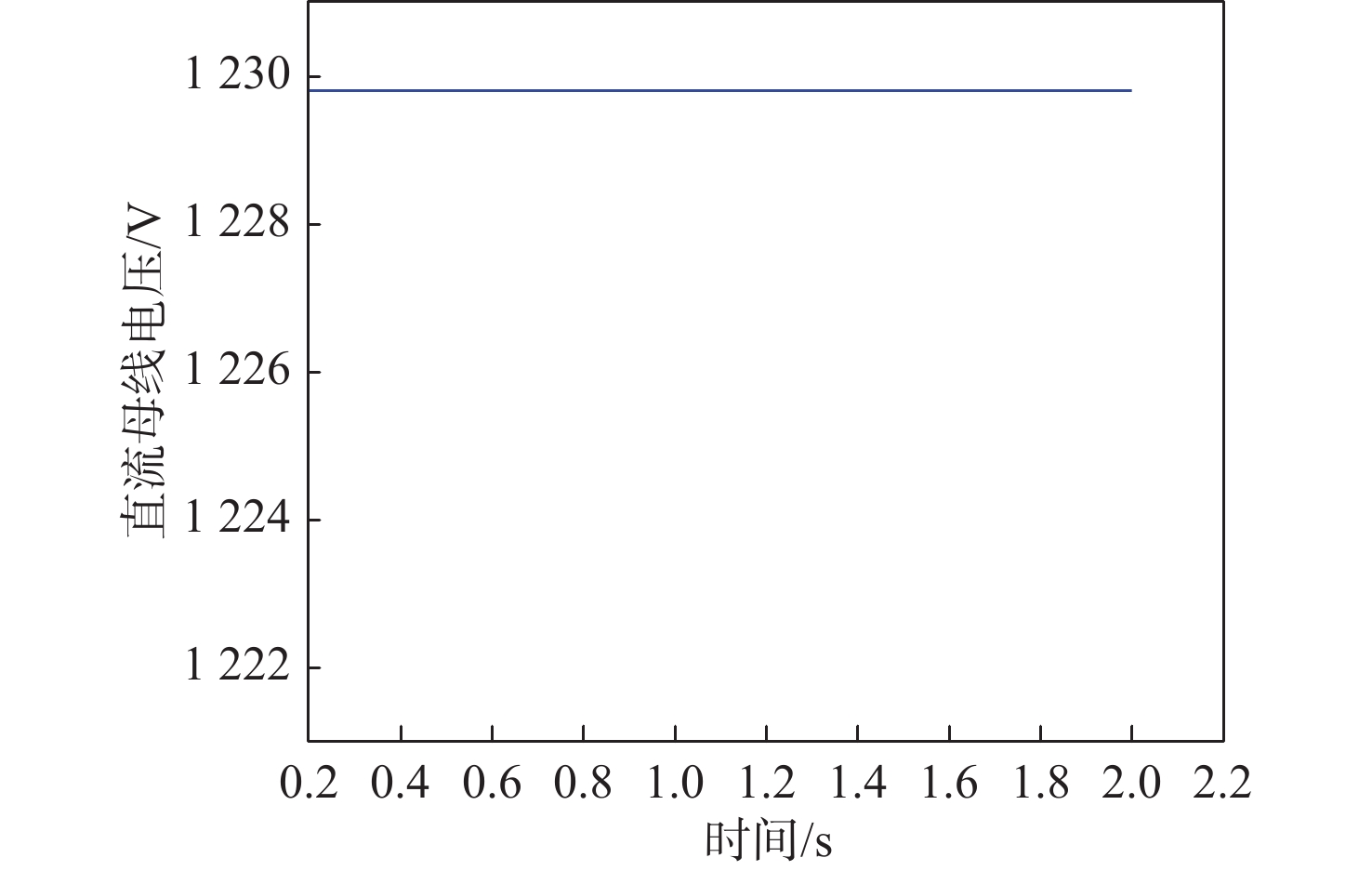
表 2 参数优化前、后的取值

Table 2. Value before and after parameter optimization

参数	优化前取值	优化后取值
k_Ip	40	31.25
k_Ii	0.1	0.26
C_f的临界稳定值/mF	5	1.26

下载: 导出CSV

| 显示表格

将优化后的控制参数与支撑电容代入仿真模型，即可得到直流母线电压的时域仿真结果，如图13所示，可知其优化后的控制参数和支撑电容在各工况下均可保证直流母线电压的稳定。

图 13 参数优化后直流母线电压的时域仿真结果

Figure 13. Time domain simulation results of DC bus voltage after parameter optimization

下载: 全尺寸图片幻灯片

5. 结　语

本文基于Middlebrook阻抗比稳定性判据，通过采用系统模型简化、非线性系统线性化处理以及将三相交流系统dq变换为直流等方法，推演得到了直流母线小信号输出阻抗、逆变器与电机的小信号输入阻抗模型，解决了舰船直流推进系统中直流母线电压的稳定性分析问题；同时，采用粒子群优化算法解决了电流控制器参数优化问题。稳定性分析结果表明：直流母线支撑电容、电阻、电感的增加或减小将影响直流母线的稳定性，进而影响整个系统的稳定性，其中直流母线支撑电容、电阻的增加和电感的减小将明显提高系统的稳定性；电流控制器的参数优化结果表明：采用粒子群优化控制器参数之后，可以在确保母线电压稳定的情况下，明显降低支撑电容取值，这对于降低舰船直流推进系统的变流器整体尺寸而言意义重大。综上所述，本文通过理论研究与仿真计算，证明了采用Middlebrook阻抗比稳定性判据研究舰船直流推进系统稳定性的可行性，该方法可以推广至电力电子化占比严重的综合电力系统电压振荡及其抑制领域的研究工作。

图 1 舰船直流推进系统的总体架构

Figure 1. Topology of ship DC propulsion system

下载: 全尺寸图片幻灯片

图 2 舰船直流推进系统的简化模型

Figure 2. Simplified model of ship DC propulsion system

下载: 全尺寸图片幻灯片

图 3 级联系统的等效模型

Figure 3. Equivalent model of cascade system

下载: 全尺寸图片幻灯片

图 4 T_m(s)的奈奎斯特曲线

Figure 4. Nyquist curve of T_m(s)

下载: 全尺寸图片幻灯片

图 5 逆变器–电机系统及其控制框图

Figure 5. Inverter motor system and its control block diagram

下载: 全尺寸图片幻灯片

图 6 PMSM矢量控制框图

Figure 6. Vector control block diagram of PMSM

下载: 全尺寸图片幻灯片

图 7 随着C_f变化的T_m(s)奈奎斯特图

Figure 7. Nyquist plot of T_m(s) as C_f changes

下载: 全尺寸图片幻灯片

图 8 随着L_f变化的T_m(s)奈奎斯特图

Figure 8. Nyquist plot of T_m(s) as L_f changes

下载: 全尺寸图片幻灯片

图 9 随着R_f变化的T_m(s)奈奎斯特图

Figure 9. Nyquist plot of T_m(s) as R_f changes

下载: 全尺寸图片幻灯片

图 10 粒子群算法的流程图

Figure 10. The flowchart of particle swarm optimization algorithm

下载: 全尺寸图片幻灯片

图 11 参数优化的流程图

Figure 11. Flowchart for parameter optimization

下载: 全尺寸图片幻灯片

图 12 参数优化的结果

Figure 12. Result graph for parameter optimization

下载: 全尺寸图片幻灯片

图 13 参数优化后直流母线电压的时域仿真结果

Figure 13. Time domain simulation results of DC bus voltage after parameter optimization

下载: 全尺寸图片幻灯片

表 1 关键性仿真参数

Table 1 Key simulation parameters

参数	数值	参数	数值
母线电容C_f/mF	10	定子电阻R_s/mΩ	1.502
母线电感L_f/mH	0.2	电感L_d，L_q/mH	0.476 7
母线电阻R_f/mΩ	1	磁极对数P_n	8
母线电压U_dc/V	1 200	永磁体磁链ψ_f/Wb	3.55
负载转矩T_L/(N·m)	195 200	转动惯量J/(kg·m²)	550
转速控制器的比例系数k_ωp	50	电流控制器的比例系数k_Ip	40
转速控制器的积分系数k_ωi	0.2	电流控制器的积分系数k_Ii	0.1

下载: 导出CSV

表 2 参数优化前、后的取值

Table 2 Value before and after parameter optimization

参数	优化前取值	优化后取值
k_Ip	40	31.25
k_Ii	0.1	0.26
C_f的临界稳定值/mF	5	1.26

下载: 导出CSV

参考文献(18)

[1]	邓林, 印德武, 李明. 综合电力系统在舰船上的应用[J]. 中国舰船研究, 2007, 2(4): 44–46. doi: 10.3969/j.issn.1673-3185.2007.04.010 DENG L, YIN D W, LI M. Application of integrated power system to SWATH ships[J]. Chinese Journal of Ship Research, 2007, 2(4): 44–46 (in Chinese). doi: 10.3969/j.issn.1673-3185.2007.04.010
[2]	范磊, 李维波, 徐聪, 等. 基于电力电子开关的智能化稳压电源补偿策略[J]. 中国舰船研究, 2018, 13(增刊1): 175–181. FAN L, LI W B, XU C, et al. Compensation strategy of intelligent regulated power supply based on power electronic converters[J]. Chinese Journal of Ship Research, 2018, 13(Supp 1): 175–181 (in Chinese).
[3]	贾志强. 基于直流电网的船舶电站高效控制策略研究[D]. 北京: 中国舰船研究院, 2016. JIA Z Q. Research on high efficiency control strategy of ship electric power station based on DC power grid[D]. Beijing: China Ship Research and Development Academy, 2016 (in Chinese).
[4]	梁正卓, 朱琬璐, 朱志宇, 等. 船舶综合电力系统重构技术现状及展望[J]. 中国舰船研究, 2022, 17(6): 36–47. doi: 10.19693/j.issn.1673-3185.02885 LIANG Z Z, ZHU W L, ZHU Z Y, et al. Situation and prospects of shipboard integrated power system reconfiguration technology[J]. Chinese Journal of Ship Research, 2022, 17(6): 36–47 (in Chinese). doi: 10.19693/j.issn.1673-3185.02885
[5]	刘金波. 舰船电力系统暂态稳定性分析[D]. 哈尔滨: 哈尔滨工程大学, 2002. LIU J B. Analysis of naval vessel electric power system transit stability[D]. Harbin: Harbin Engineering University, 2002 (in Chinese).
[6]	滕昌鹏. 直流微网的稳定性及功率协调控制研究[D]. 济南: 山东大学, 2019. TENG C P. Large-signal stability analysis of DC microgrid and research on power coordinated control strategy[D]. Ji'nan: Shandong University, 2019 (in Chinese).
[7]	JAVAID U, FREIJEDO F D, DUJIC D, et al. Dynamic assessment of source-load interactions in marine MVDC distribution[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4372–4381. doi: 10.1109/TIE.2017.2674597
[8]	周于清, 李大虎, 姚伟, 等. 受端近区光伏电站对LCC-HVDC系统稳定性影响分析[J]. 中国电力, 2024, 57(3): 170–182. ZHOU Y Q, LI D H, YAO W, et al. Stability analysis of LCC-HVDC with PV station at the receiving end[J]. Electric Power, 2024, 57(3): 170–182 (in Chinese).
[9]	杨继沛, 杨苓, 魏茂华. 基于有源电容的直流母线电压振荡抑制器及其控制方法[J/OL]. 上海交通大学学报: 1−22 [2024-03-07]. https://doi.org/10.16183/j.cnki.jsjtu.2023.327. YANG J P, YANG L, WEI M H. DC bus voltage oscillation suppressor based on active capacitor and its control method[J/OL]. Journal of Shanghai Jiaotong University: 1−22 [2024-03-07]. https://doi.org/10.16183/j.cnki.jsjtu.2023.327 (in Chinese).
[10]	杨国朝, 杨朝雯, 刘仲英, 等. 直流配网用级联DC-DC变换系统稳定性分析[J]. 电气传动, 2021, 51(20): 24–28,35. YANG G C, YANG C W, LIU Z Y, et al. Stability analysis of cascaded DC-DC converter system for DC distribution network[J]. Electric Drive, 2021, 51(20): 24–28,35 (in Chinese).
[11]	刘胜, 程垠钟. 基于小信号模型的船舶中压直流发电系统稳定性分析[J]. 中国电机工程学报, 2015, 35(8): 1930–1939. LIU S, CHENG Y Z. Small signal model based stability analysis for shipboard medium voltage DC generation systems[J]. Proceedings of the CSEE, 2015, 35(8): 1930–1939 (in Chinese).
[12]	JIANG X F, HAN X Y, JIANG P, et al. The parameters optimization and stable boundary expansion method of current controller for VSC to avoid low frequency oscillations[J]. Energy Reports, 2023, 9(Supp 8): 422-431.
[13]	储天舒, 王志国, 刘飞. 基于子空间非参数模型的PID控制器性能优化[J/OL]. 控制工程: 1−9 [2024-03-07]. https://doi.org/10.14107/j.cnki.kzgc.20220722. CHU T S, WANG Z G, LIU F. Performance optimization of PID controller based on subspace nonparametric model [J/OL]. Control Engineering of China: 1−9 [2024-03-07]. https://doi.org/10.14107/j.cnki.kzgc.20220722 (in Chinese).
[14]	杨建, 刘笑, 董密, 等. 基于深度学习的恒功率负荷直流微电网稳定性分析[J]. 电力系统自动化, 2023, 47(15): 188–197. YANG J, LIU X, DONG M, et al. Deep learning based stability analysis of DC microgrid with constant power loads[J]. Automation of Electric Power Systems, 2023, 47(15): 188–197 (in Chinese).
[15]	魏威, 郑华俊, 袁旭峰, 等. 基于平方和规划的带恒功率负载的直流微电网大信号稳定性分析[J]. 电网与清洁能源, 2023, 39(8): 27–35. doi: 10.3969/j.issn.1674-3814.2023.08.004 WEI W, ZHENG H J, YUAN X F, et al. An analysis of large signal stability of the DC microgrid with constant power load based on sum of squares programming[J]. Power System and Clean Energy, 2023, 39(8): 27–35 (in Chinese). doi: 10.3969/j.issn.1674-3814.2023.08.004
[16]	ZHANG D D, YU J Y, DU A N, et al. A weighting-factorless predictive torque control method for open-end winding PMSM with common DC bus[J]. Journal of Physics: Conference Series, 2023, 2530: 012028. doi: 10.1088/1742-6596/2530/1/012028
[17]	王燕平, 王艳芳. 自动控制原理[M]. 北京: 人民邮电出版社, 2015: 192. WANG Y P, WANG Y F. Automatic control principle[M]. Beijing: Posts & Telecom Press, 2015: 192(in Chinese).
[18]	ZHANG L G, LI H, SHAN L Q, et al. Double-hierarchical fuzzy exponential convergence law fractional-order sliding mode control for PMSM drive control in EV[J]. Engineering Science and Technology, an International Journal, 2023, 47: 101536. doi: 10.1016/j.jestch.2023.101536

施引文献

资源附件(0)

图(13) / 表(2)

计量

文章访问数: 87
HTML全文浏览量: 44
PDF下载量: 20
被引次数: 0

0. 引　言
1. 电力电子化舰船的直流推进系统模型
1.1 舰船直流推进系统的总体架构
1.2 系统简化模型
2. 电力电子化舰船直流推进系统的稳定性机理分析
2.1 直流母线的振荡机理分析
2.2 Middlebrook稳定性分析方法
2.2.1 Middlebrook阻抗比判据分析
2.2.2 直流母线侧的输出阻抗模型分析
2.2.3 推进电机阻抗的模型分析
3. 推进系统的稳定性分析
4. 粒子群算法优化控制器参数
4.1 粒子群优化算法
4.2 粒子群算法优化目标函数
4.3 粒子群算法优化参数
5. 结　语

0. 引　言
1. 电力电子化舰船的直流推进系统模型
1.1 舰船直流推进系统的总体架构
1.2 系统简化模型
2. 电力电子化舰船直流推进系统的稳定性机理分析
2.1 直流母线的振荡机理分析
2.2 Middlebrook稳定性分析方法
2.2.1 Middlebrook阻抗比判据分析
2.2.2 直流母线侧的输出阻抗模型分析
2.2.3 推进电机阻抗的模型分析
3. 推进系统的稳定性分析
4. 粒子群算法优化控制器参数
4.1 粒子群优化算法
4.2 粒子群算法优化目标函数
4.3 粒子群算法优化参数
5. 结　语

参考文献(18)

施引文献

资源附件(0)

基于Middlebrook的舰船电力电子化推进系统的稳定性分析和控制器参数优化方法

作者简介: 徐成虎，男，2000年生，硕士生。研究方向：电子信息。E-mail：3269180036@qq.com 李维波，男，1973年生，博士，教授，博士生导师。研究方向：电力电子技术在能源系统中的应用。E-mail：liweibo@whut.edu.cn

通讯作者: 李维波

计量

出版历程

Stability analysis and controller parameter optimization method for ship power electronic propulsion system based on Middlebrook criterion

0. 引 言

1. 电力电子化舰船的直流推进系统模型

1.1 舰船直流推进系统的总体架构

1.2 系统简化模型

2. 电力电子化舰船直流推进系统的稳定性机理分析

2.1 直流母线的振荡机理分析

2.2 Middlebrook稳定性分析方法

2.2.1 Middlebrook阻抗比判据分析

2.2.2 直流母线侧的输出阻抗模型分析

2.2.3 推进电机阻抗的模型分析

3. 推进系统的稳定性分析

4. 粒子群算法优化控制器参数

4.1 粒子群优化算法

4.2 粒子群算法优化目标函数

4.3 粒子群算法优化参数

5. 结 语

计量

出版历程

目录

0. 引 言

1. 电力电子化舰船的直流推进系统模型

1.1 舰船直流推进系统的总体架构

1.2 系统简化模型

2. 电力电子化舰船直流推进系统的稳定性机理分析

2.1 直流母线的振荡机理分析

2.2 Middlebrook稳定性分析方法

2.2.1 Middlebrook阻抗比判据分析

2.2.2 直流母线侧的输出阻抗模型分析

2.2.3 推进电机阻抗的模型分析

3. 推进系统的稳定性分析

4. 粒子群算法优化控制器参数

4.1 粒子群优化算法

4.2 粒子群算法优化目标函数

4.3 粒子群算法优化参数

5. 结 语

作者简介:
徐成虎，男，2000年生，硕士生。研究方向：电子信息。E-mail：3269180036@qq.com

李维波，男，1973年生，博士，教授，博士生导师。研究方向：电力电子技术在能源系统中的应用。E-mail：liweibo@whut.edu.cn

通讯作者:
李维波

0. 引　言

5. 结　语

0. 引　言

5. 结　语