0.   引　言

随着我国“交通强国”和“海洋强国”战略的提出，船舶智能化迎来新的发展机遇，智能船舶自主航行技术受到工业和海事企业的广泛关注。中国船级社发布的《智能船舶规范（2023）》^[1]明确了智能船舶的智能航行、智能能效管理等主要功能；国务院发布的《气象高质量发展纲要2022—2035》^[2]将远洋气象导航列入国家气象高质量发展纲要，提出海洋强国气象保障行动，旨在增强国家气象导航服务能力，为船舶运输提供气象信息保障服务。船舶航线规划和优化是气象导航和智能航行功能中的核心关键技术之一，可为船舶高效航行提供保障，提高营运效益。

目前，船舶航线规划采用的方法包括等时线法、图形搜索算法以及智能优化算法等。等时线法由James^[3]提出，最早只能求解最短航时航线。Hagiwara等^[4]对等时线法进行了改进，使其能够解决最短航行时间与最少燃油消耗的航线优化问题。动态规划法将问题分解为若干阶段并分段求解，涉及多级决策优化过程，常用于船舶航线规划。如Zaccone等^[5]在三维动态规划的基础上提出一种新的航次优化方法，该方法综合考虑气象条件、船舶运动特性及人员舒适性，可求解船舶航次最低油耗航线及航速剖面。图形搜索算法如Dijkstra算法和A*算法等也广泛应用于智能船舶的航线优化。张大恒^[6]使用改进Dijkstra算法选择船舶最优航线；崔金龙等^[7-8]通过改进A*算法对船舶航向航速进行协同优化，实现了船舶安全避离大风浪危险区域的同时降低船舶燃油消耗。

随着信息技术的快速发展，智能优化算法在航线优化领域的应用逐渐增多。李明峰^[9]以最短航行时间和最低燃油消耗为优化目标，采用遗传算法求解最佳船舶航线。Wang等^[10]设计了一种结合船舶运动特性约束的二次优化遗传算法，对船舶航线进行规划。崔康靖等^[11]考虑风、浪双重气象因素，使用人工势场法和模拟退火算法对船舶航线的航时和航程进行优化。Zhang等^[12]以航时和航行风险为优化目标，改进多目标蚁群算法进行船舶航路优化。Zhao等^[13]基于改进的粒子群算法进行船舶航线多目标规划，并建立多目标最优船舶气象航线系统框架。李小刚^[14]以航程、航时和油耗作为优化目标，分析海上风、浪和流对船舶失速特性的影响，运用遗传算法求解航线。童帮裕^[15]以航行距离、航行操作以及流冰规避为航线优化目标，建立多目标航线规划模型，对海冰覆盖的冰区航道进行航线规划。Szlapczynska^[16]考虑时间、能耗和安全性等约束条件，采用Pareto优化方法获得最优航线规划方案。Chen^[17]提出一种基于场理论的多目标路径优化算法，构建以安全、经济、环境保护为目标的北极航线设计。Ma^[18]提出一种改进的基于cell的方法，以总航行成本最小为目标，对船舶在排放控制区（ECA）内航行进行航线和航速优化，以降低ECA内的总成本和船舶排放。

目前，航线多目标优化已成为船舶航线规划领域的研究重点，旨在多个约束条件下同时优化多个目标。然而，由于船舶跨洋航线航时长且气象海况复杂，单一优化算法的效果不理想^[19]。主要体现在智能算法具有快速求解的优势，但每次运行求解得出的近似最优解不同，给使用人员带来困扰；而精确算法虽能得出最优解，但对优化空间较大的跨洋航线求解速度慢。因此，本文拟综合A*算法与非支配排序遗传算法（NSGA-II）的优点，建立船舶航线多目标优化模型，在较短时间内生成最优航线Pareto前沿面。以期根据航次任务规划航线并选择适用航线，从而减少人为失误，提高船舶航行的安全性、经济性和可靠性。

1.   环境数据模型及优化目标

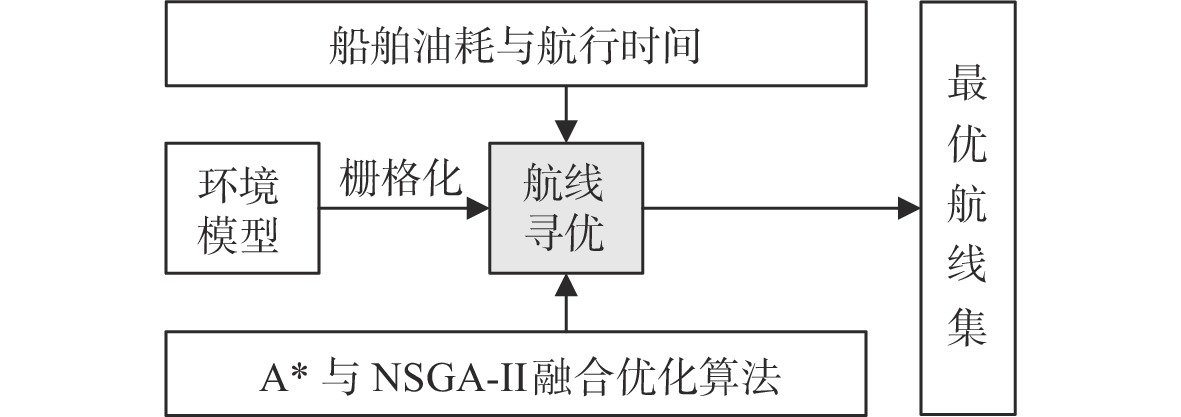
船舶航线优化模型和算法流程如图1所示。首先利用船舶航行环境数据建立环境栅格化模型，然后建立船舶油耗和航行时间的优化目标函数，最后使用A*与NSGA-II融合算法进行路径寻优并得出从起点到终点的Pareto最优航线解集。

图  1  模型和算法整体流程

Figure  1.  Overall process of the model and algorithm

下载: 全尺寸图片 幻灯片

1.1   环境数据模型

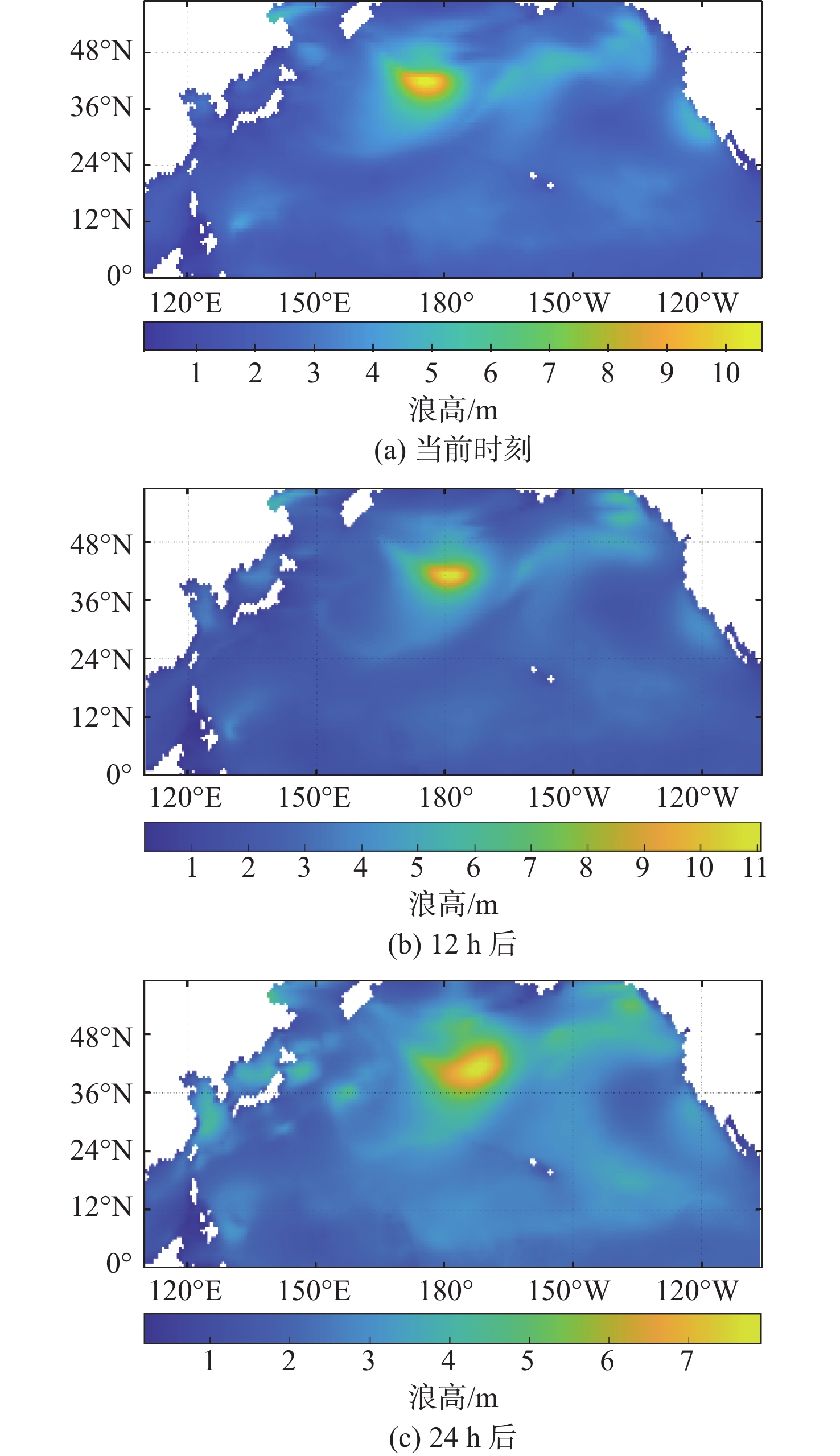
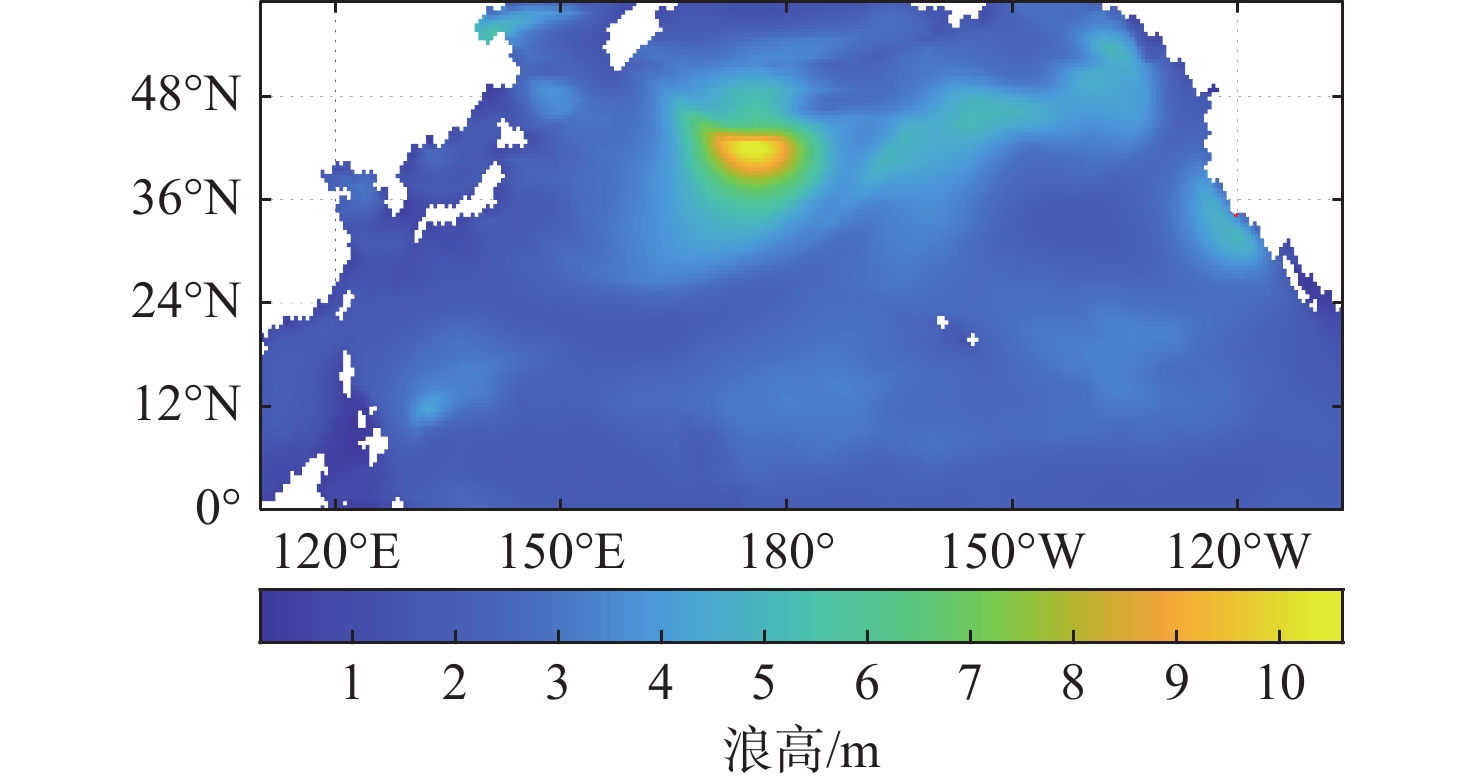
远洋航行船舶受到水深、风、浪等环境因素影响，环境数据模型是进行船舶航线规划的基础。本文基于水深数据和气象水文数据进行建模，其中气象地理数据分别来源于欧洲中期天气预报中心和通用大洋水深制图提供的数据。获取的数据为Grid和NetCDF格式的格点数据，数据精度为0.5°×0.5°，采用Matlab编程实现的可视化效果如图2所示，颜色鲜艳的区域为锋面气旋引起的大浪区，连续时刻的变化趋势表明了大浪区的动态变化。

图  2  可视化气象和地理信息

Figure  2.  Visualized meteorological and geographic information

下载: 全尺寸图片 幻灯片

为提高航线寻优效率，采用栅格法对航行环境进行处理，将其转换为具有简单几何关系的环境气象模型，按照环境数据0.5°*0.5°的精度采用二值法对海域进行处理并分类。首先，将可航栅格设置为1，称为自由网格；将不可航栅格设置为0，称为受限网格。同时，综合考虑航行区域的风速、浪高、水深以及船舶的吃水限制和抗风浪能力，进一步判断自由网格是否可以满足船舶航行要求，将不满足要求的网格设置为不可航行网格，栅格点的处理如式(1)所示。

式中：$\varphi$为纬度；λ为经度；t为时间。

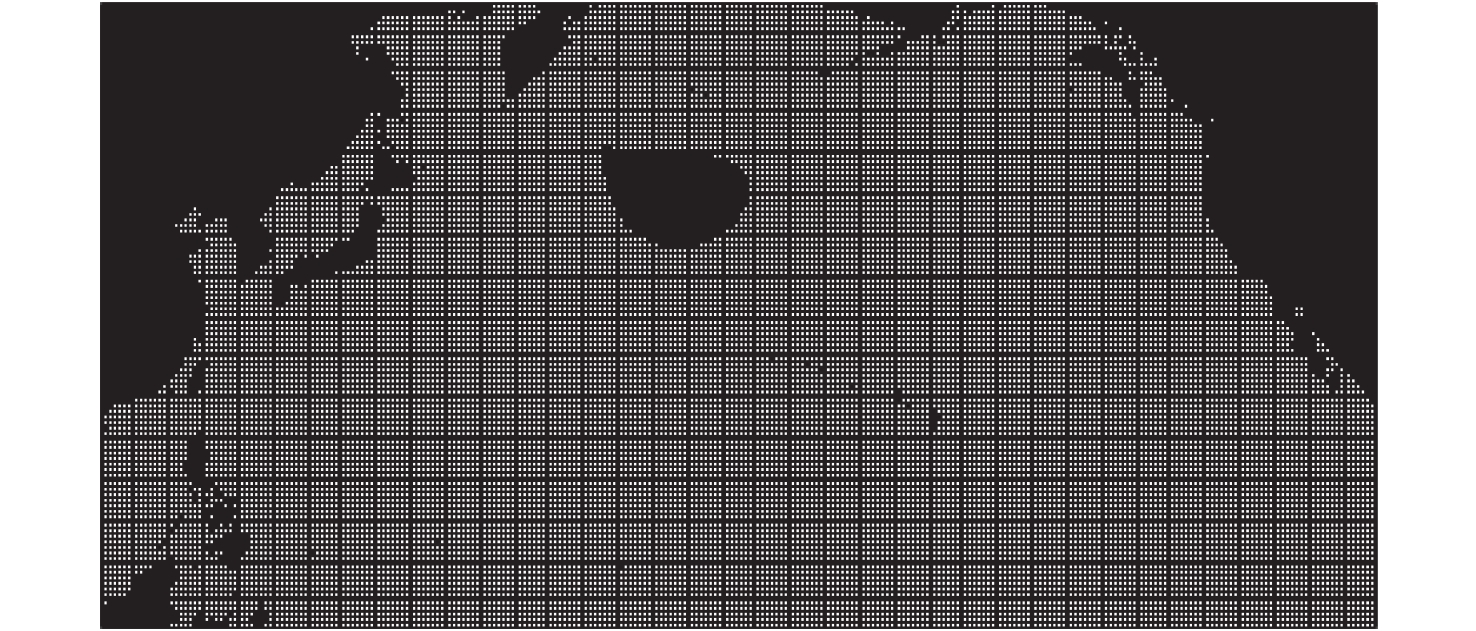
在风浪场景下，风浪阈值由使用人员根据实际船舶特性和航次任务进行设置，并作为约束条件输入。结合船舶性能和风浪信息，判断各待航格点在t时刻的风浪信息是否满足船舶航行要求，若不满足，则将该格点设置为不可航点，亦为$N(\varphi ,\lambda ,t) = 0$。图2（a）中二值化后的海域环境如图3所示，图中黑色部分为不可航行区域，白色部分为可航区域。

图  3  航行环境二值化图

Figure  3.  Binarization of navigation environment

下载: 全尺寸图片 幻灯片

1.2   优化目标

在满足航行安全的前提下，节约航次燃油消耗并缩短航行时间是远洋船舶降低运营成本和提高经济效益的重要手段。船舶燃油消耗与航行时间通过航向和航速决策变量相互制约，航线规划需要综合考虑燃油消耗和航行时间，并寻求最优平衡点，因此，船舶航线规划问题属于多目标优化问题。

在船舶航线优化设计过程中，航线节点之间的距离与各节点的经纬度位置信息相关。为更准确地计算整条航线的航程，使用相邻节点i与i+1之间的大圆距离度量其航程d_i，并依次累加得到整条航线的航程。

式中：R为地球半径，取为6371 km；d_i为节点$\left( {{\varphi _i},{\lambda _i}} \right)$与$\left( {{\varphi _{i + 1}},{\lambda _{i + 1}}} \right)$之间的航程。

根据各航段的航程和船舶在各个航段内的航行速度，利用式(3)计算总航行时间。

式中：T为总航行时间；v_i为各航段的对地速度；n为航线上航路点的数量。

船舶燃油消耗率与气象、海况、航速及装载状态等因素相关。我们前期构建了基于XGBoost算法的船舶油耗预测模型，可通过航速、气象信息等因素计算各个航段内的船舶燃油消耗率。进而，利用式(4)计算船舶在整条航线上的燃油消耗。

式中：F_i和T_i分别为航线上第i个航段的船舶燃油消耗率和航行时间；F为船舶在整条航线上的燃油总消耗量。

2.   船舶航线多目标优化算法

船舶跨洋航线规划的时间、空间跨度大，且受风浪等环境因素影响，导致航线寻优空间较大，问题求解复杂。为解决这一问题，本文提出一种融合A*算法与NSGA-II算法优点的船舶航线多目标优化算法，以实现船舶航线的多目标优化和高效寻优。

2.1   NSGA-II

NSGA-II是基于Pareto最优理念的一种遗传算法，它通过不断演化和进化生成一组非支配解集，这些解集在多个目标函数上都是最优的，即没有其他解可以同时更好地满足所有目标^[20]。NSGA-II通过快速非支配排序和拥挤度距离的机制，能够在多个目标函数间实现有效的权衡，并生成一组多样性好、分布均匀的非支配解集，为决策提供多个最优选择；此外，与NSGA相比，NSGA-II采用了精英保留策略，保证优良的种群个体在进化过程中不会被丢弃，保证种群多样性，也提高了优化结果的准确性。这使得NSGA-II成为解决多目标优化问题的有效工具。

本文使用NSGA-II求解最优航线的具体操作如下：

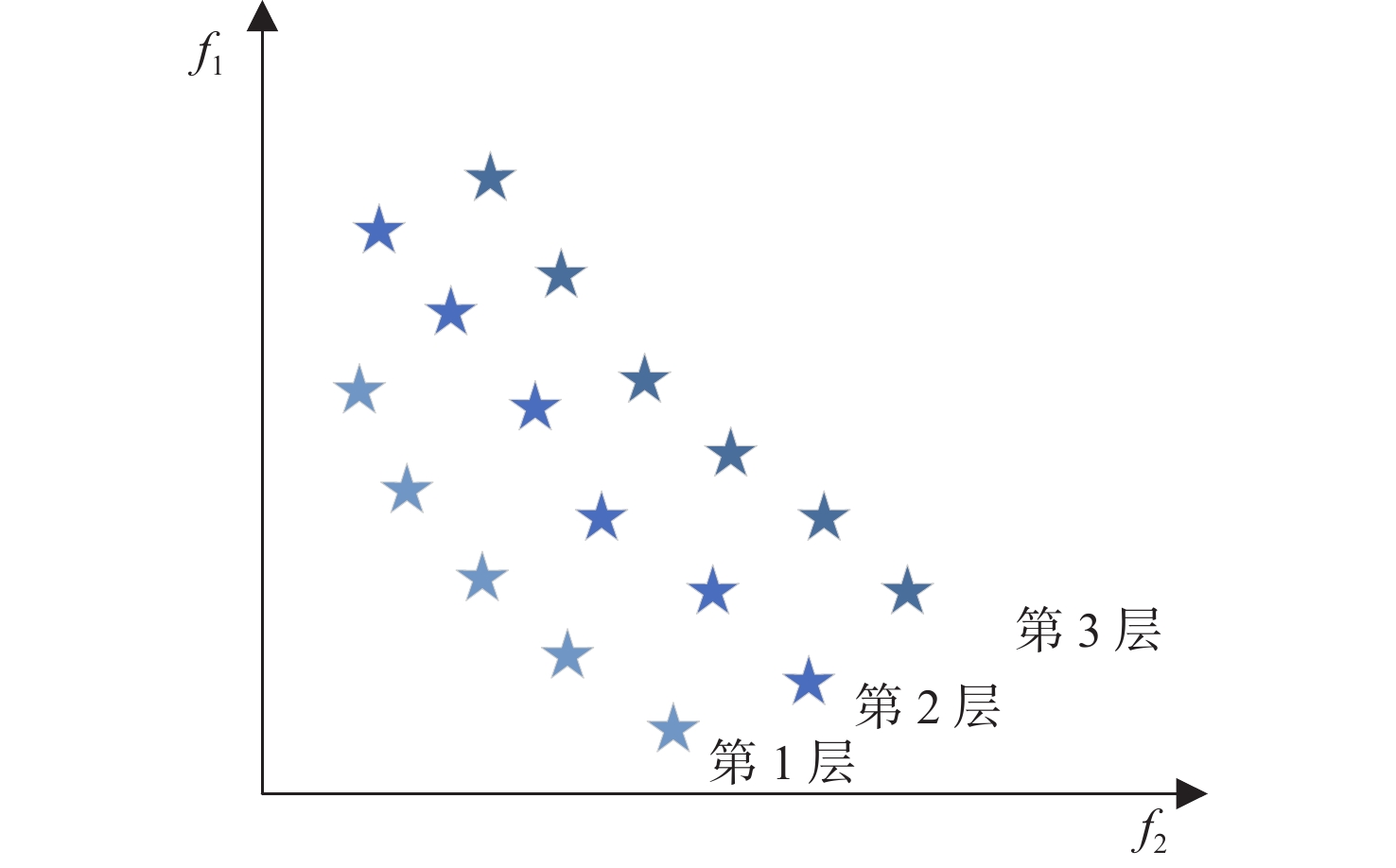
1） 快速非支配排序。根据航线种群染色体的优劣程度将其分为不同等级的层级，第1层优于第2层和第3层，且该层是航线种群的Pareto最优航线解集，如图4所示，图中f₁为燃油消耗，f₂为航时。

图  4  非支配分层排序

Figure  4.  Non-dominant hierarchical sorting

下载: 全尺寸图片 幻灯片

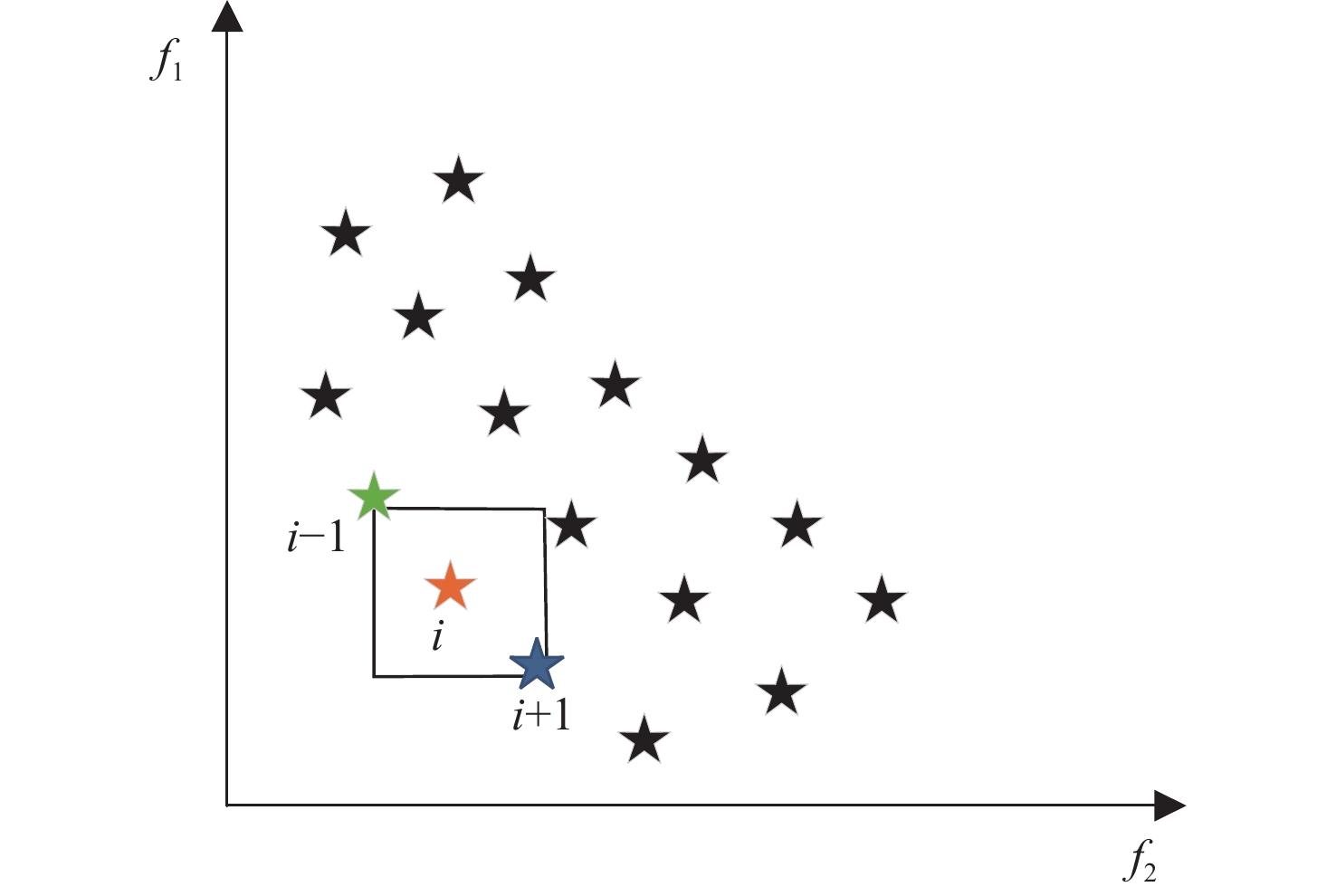
2） 拥挤度计算。通过使用拥挤距离来描述同层航线个体的分布密度，以实现对同层航线个体间的比较，从而保持航线的多样性。航线个体i的拥挤距离表示个体i与相邻两个航线个体的所有目标函数之差的和。拥挤距离越大表示航线种群的多样性越大，如图5所示。

图  5  拥挤度计算

Figure  5.  Congestion calculation

下载: 全尺寸图片 幻灯片

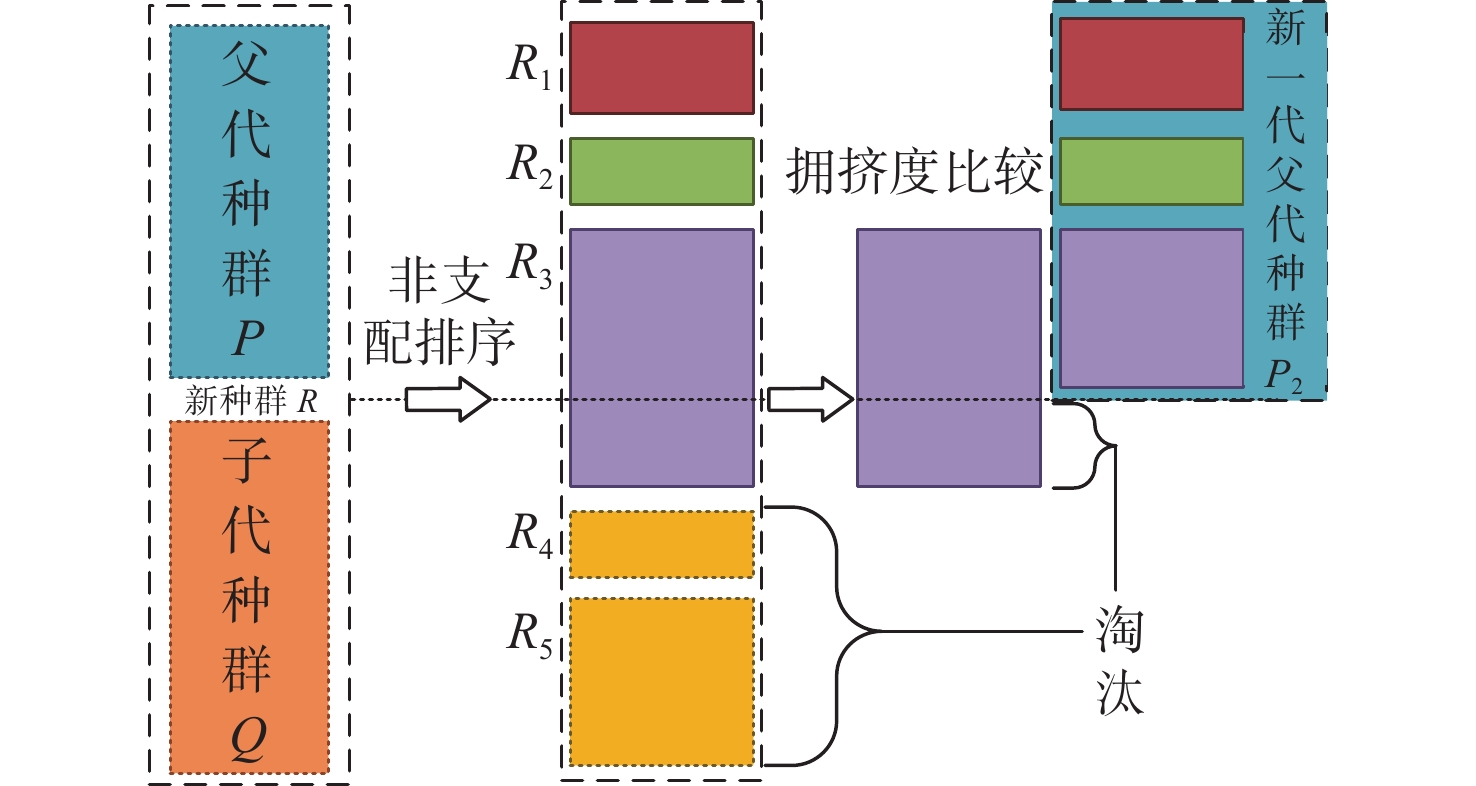
3） 精英保留策略。精英保留策略有利于将航线种群中的优良个体延续到下一代，加快航线种群进化的速度。将父代航线种群P（种群规模为N）与父代产生的子代种群Q（种群规模为N）组合成种群规模为2N的新航线种群R；然后，对种群R的航线个体进行快速非支配排序（R₁，R₂，…，R₅）并计算拥挤距离，并根据航线个体的优劣程度从高到低进行排序；最后，选取前N个航线个体形成新一代的父代航线种群P₂（图6）。

图  6  精英保留策略

Figure  6.  Elite retention strategy

下载: 全尺寸图片 幻灯片

2.2   A*算法

A*算法是一种经典高效的路径规划算法，通过加入启发式函数预估未来路径的行进成本以引导搜索方向，从而缩小搜索空间^[21]。该算法从起点向附近的子节点扩展，通过评估函数选取代价值最小的节点作为下一父节点，重复此过程直到搜索到终点，完成路径规划并生成最终路径。启发函数的表达式为

式中：$F(n)$为从起点经任意节点n到达终点的代价估计；$G(n)$为起点到栅格点n的实际代价评估；$H(n)$为栅格n到终点最佳线路的代价评估。

2.3   算法融合

由于远洋航行中气象情况和海洋状况变化多端，导致航行区域栅格化后的环境气象模型庞大且复杂，一般算法无法进行高效寻路。NSGA-II作为一种全局优化算法，在迭代过程中，通过交叉操作和变异操作生成新的航线个体，能够不断扩大搜索范围，避免陷入航线优化的局部最优解。然而，在航线规划中，NSGA-II易受初始种群影响，存在收敛困难、波动幅度大及计算耗时长的问题。A*算法使用启发式函数引导路径搜索方向，可避免对整个搜索空间的盲目搜索，显著提高搜索效率。

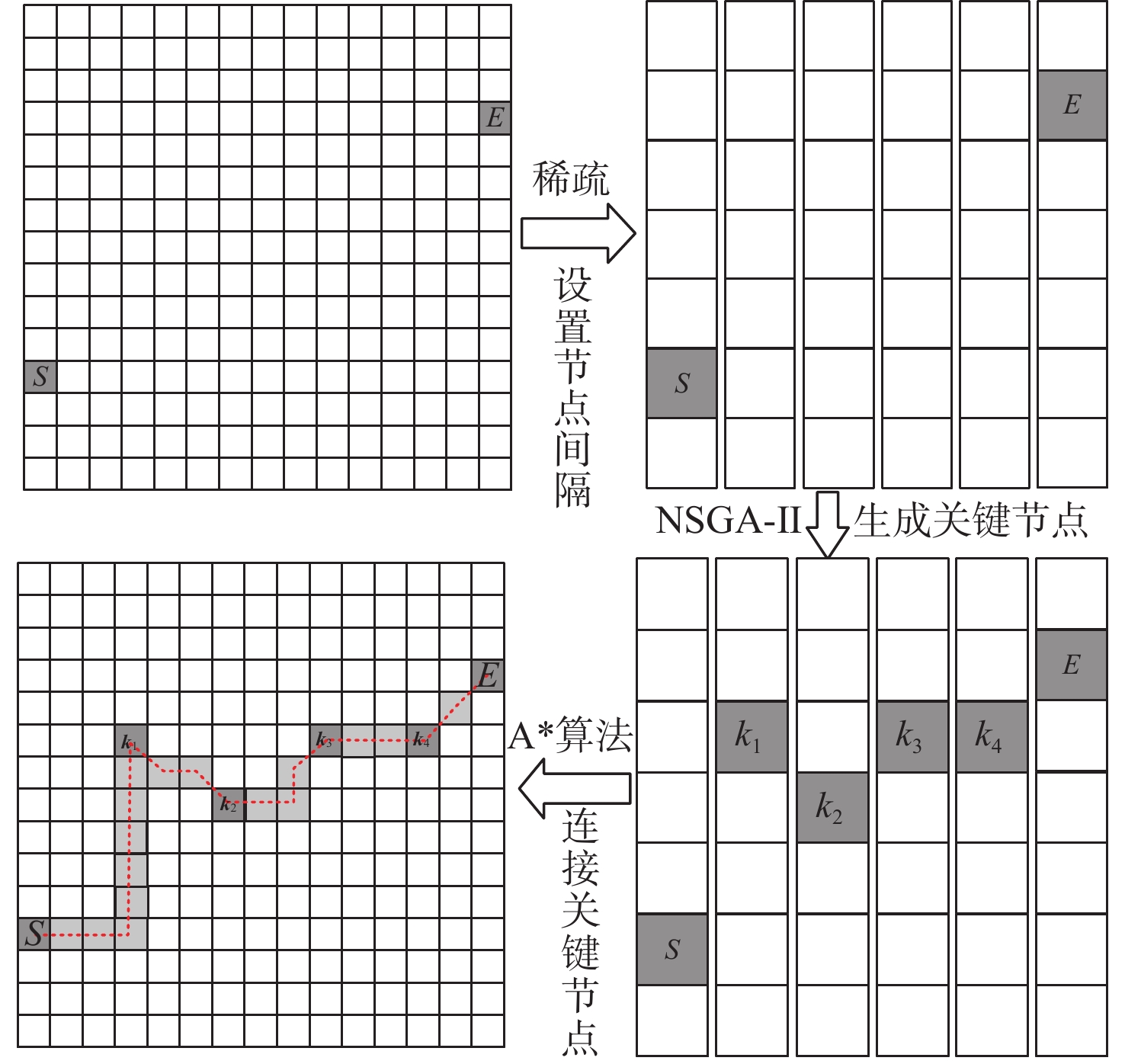
因此，本文将A*算法与NSGA-II算法的优点进行结合，提出一种结合启发式算法与精确算法的智能混合算法，以NSGA-II算法为基础生成船舶航线的关键节点，然后采用A*算法在关键节点之间寻找最佳路径。NSGA-II与A*融合算法设计思想如图7和图8所示。

图  7  航线关键节点

Figure  7.  Key nodes of the route

下载: 全尺寸图片 幻灯片

图  8  航线寻优模型

Figure  8.  Route optimization model

下载: 全尺寸图片 幻灯片

NSGA-II与A*融合算法的具体步骤如下：

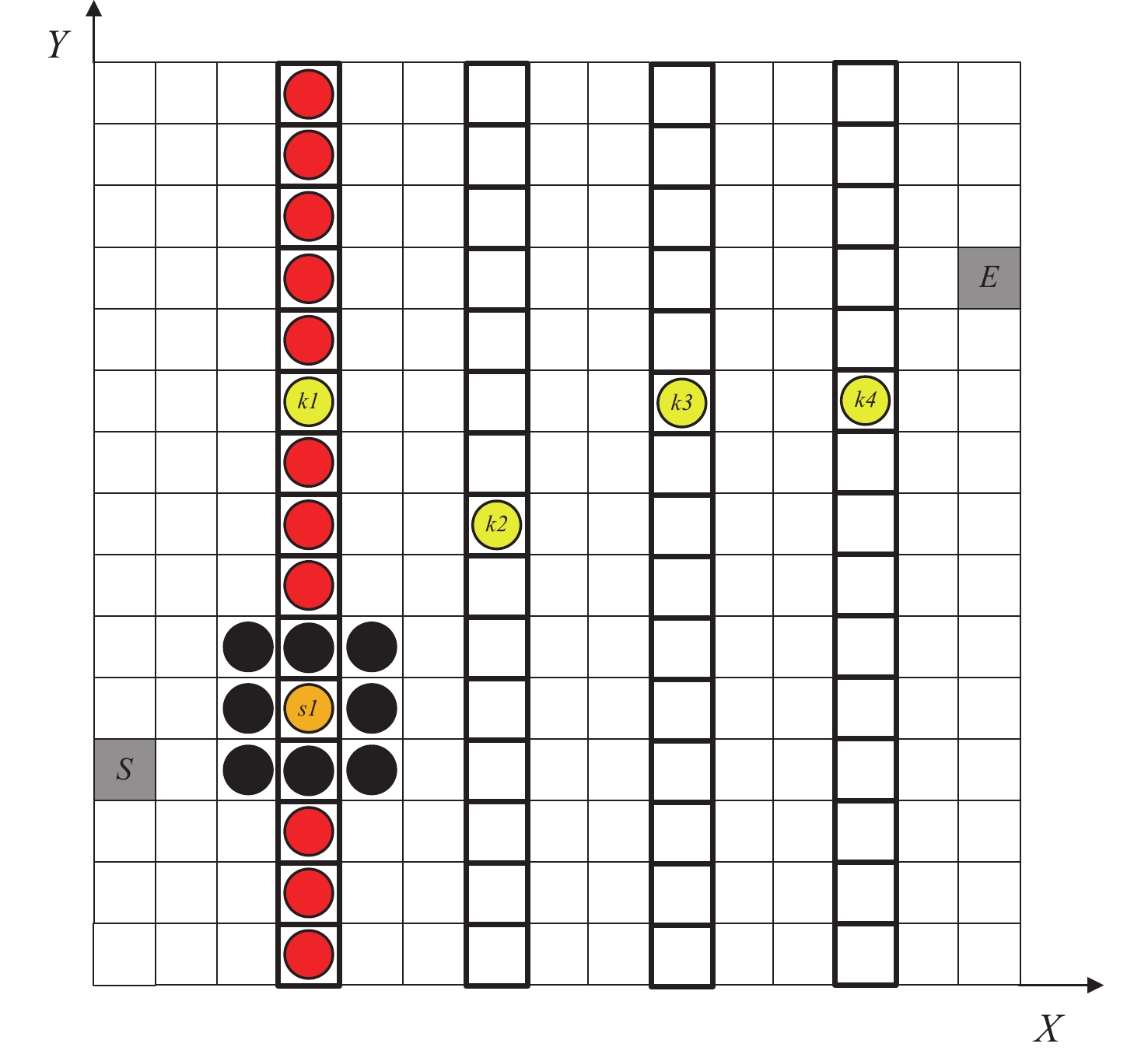
1） 网格化航行环境。对船舶航行海域进行栅格化处理，生成具有坐标标识的二维网格图，如图7所示，S和E分别为航行起点和航行终点，并设置船舶航行的纬度（Y方向）取值范围。

2） 设置间隔节点，构建稀疏栅格图。鉴于NSGA-II算法的遗传特性，航路点的选取和优化过程具有较大的随机性，因此需设置关键节点以缩小运算深度。在X轴方向上设置相同间隔的关键点，如图7黑色加粗线条所示。可根据需求调整节点数量，从而控制船舶航段数量。航段数量越多，航线精细化程度越高。如从日本到旧金山是航线中，可将横坐标划分为每4个经度或者10个经度为1个航段。

3） 采用NSGA-II生成关键节点。首先，对间隔节点s₁所在列上所有网格点进行判断，若其周围存在可航路径，则将其加入备选航路关键节点集合（红色圆圈）；否则，将其舍弃。如图7中s₁网格点周围全是障碍点（黑色），不存在可航路径，则s₁不能作为备选航路关键节点。然后，使用随机函数从备选航路关键节点集合中随机选取一个点作为关键节点，例如黄色圆圈k₁。依此类推，选择k₂，k₃和k₄作为船舶航线规划中的关键节点。

4） 采用A*寻路连接关键节点。在步骤3）中生成关键节点之后，使用A*算法寻找节点S，K（k₁，k₂，k₃和k₄）和E之间的路径，形成一条完整的船舶航线S-x-x-x-k₁-x-x-x-······-k₄-x-x-x-E。

重复步骤3）和4）进行航线迭代，生成最优航线Pareto解集。在航线寻优过程中，在所有航段上随机生成该航段的对地速度，将航线从二维扩展到三维，节点与节点之间不仅包含航向信息、气象信息和燃油消耗信息，还具备指导船舶航行的航速信息。由此，形成从出发点到目标点之间具有不同航路和不同速度的完整航线。

3.   仿真验证

3.1   实验参数设置

本文采用Matlab 2020b平台对提出的船舶航线优化模型和混合算法进行仿真验证。仿真实验的航行区域为北太平洋海域（横滨―洛杉矶）。试验船舶参数如表1所示。仿真实验参数如表2所示，其中最小吃水设定为14 m，最大浪高设定为6 m（“巨浪”级别），风力设定为35 kn（“大风”级别）。NSGA-II算法参数设置如表3所示。

表  1  船舶参数

Table  1.  Vessel parameters

参数	船长/m	船宽/m	设计吃水/m	船舶排水量/m3
数值	348	51.2	13.5	169 700

下载: 导出CSV 

| 显示表格

表  2  实验参数

Table  2.  Experimental parameters

起点	终点	对地 航速/kn	最大 风速/kn	最大 浪高/m	最小 吃水/m
[35°27′N, 139°38′E]	[33°43′N, 118°16′W]	[12, 20]	35	6	14

下载: 导出CSV 

| 显示表格

表  3  NSGA-II算法参数

Table  3.  Parameters of NSGA-II algorithm

种群数	交叉率	变异率	迭代次数
200	0.6	0.2	200

下载: 导出CSV 

| 显示表格

3.2   实验结果分析

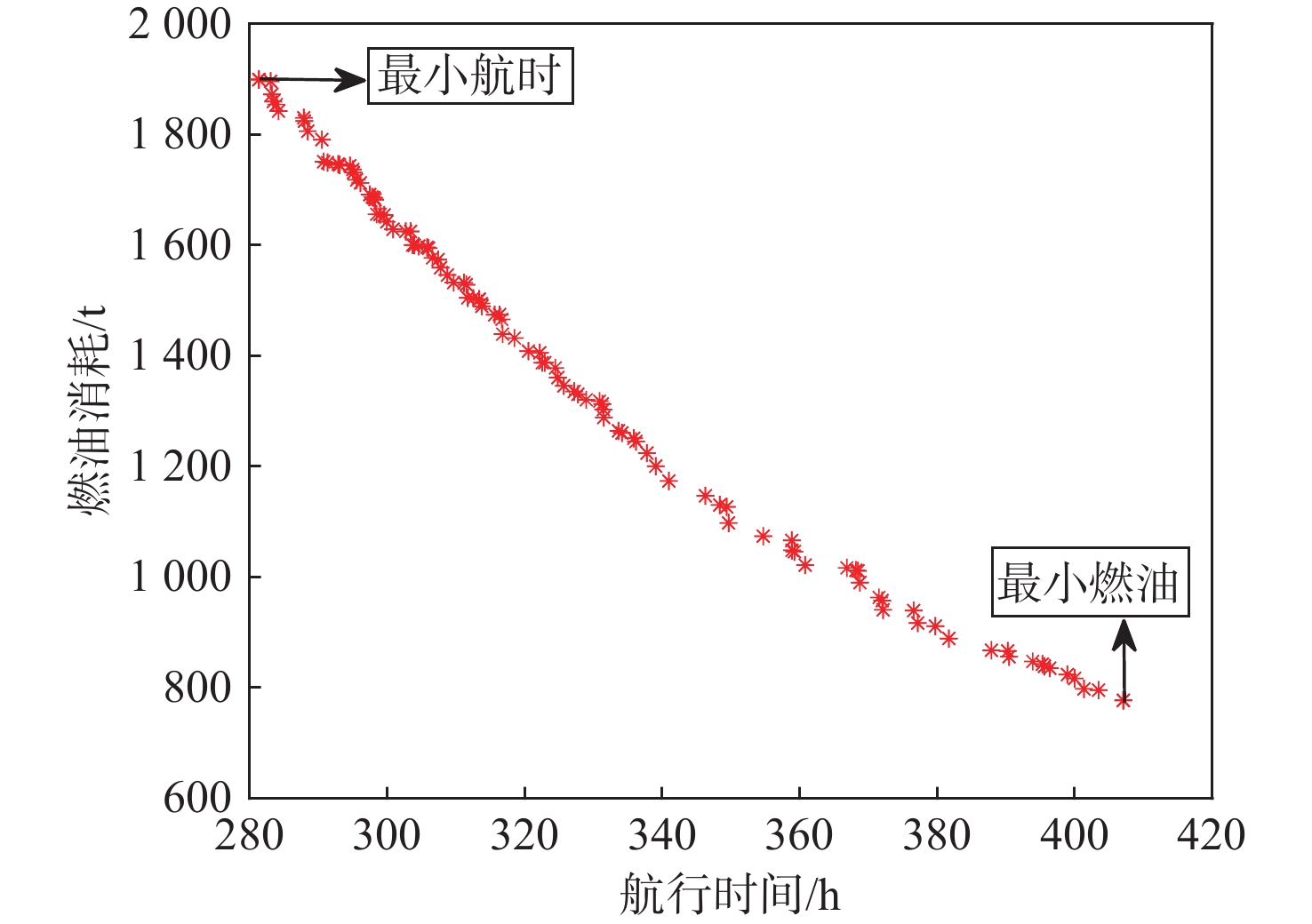
通过仿真实验计算得到的船舶航线Pareto前沿面如图9所示。Pareto前沿面上的每一个点均代表一条船舶航线，且每条航线在优化目标上均为非支配解。由图可以看出，图中船舶航线的Pareto前沿面分布结果较好，解具有多样性和丰富性，最左侧的点表明船舶燃油消耗最多，但航时最短；最右侧的点表明在此航线上船舶燃油消耗最少，但航时最长。

图  9  船舶航线Pareto前沿面

Figure  9.  Pareto front surface of ship route

下载: 全尺寸图片 幻灯片

求解得到的Pareto航线集合可视化结果如图10所示。从图中可以看出，所有航线的整体走势趋向于大圆航线，且在前段均能有效避开大风浪区域（图中颜色鲜艳的区域，浪高大于6 m），在后段接近大圆航线，符合航海实际需求。

图  10  Pareto航线集合可视化

Figure  10.  Visualization of Pareto route collection

下载: 全尺寸图片 幻灯片

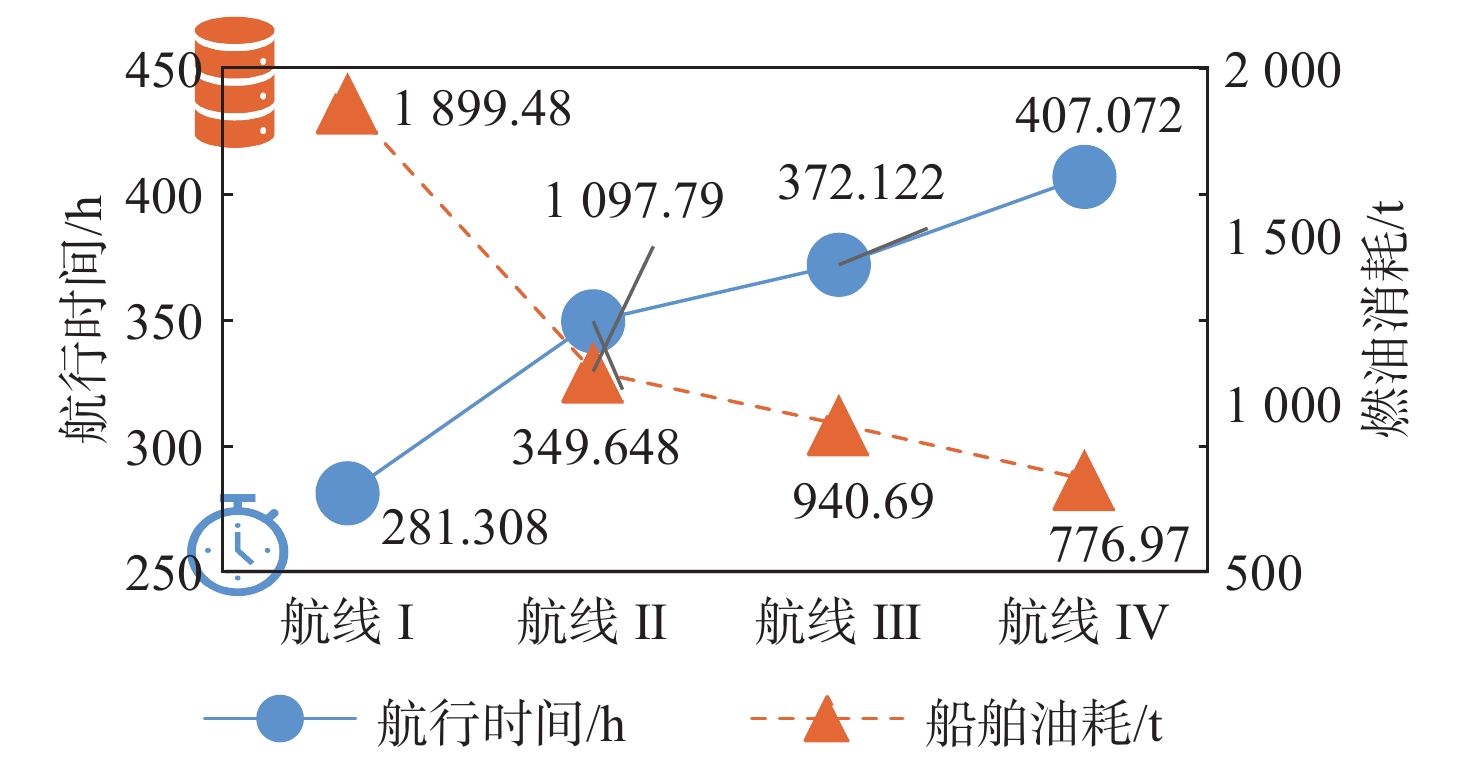
Pareto最优航线前沿面上的每条最优航线具有不同的航时和燃油消耗特性。船舶驾驶员可根据具体的航次任务选择不同的航线，如最小燃油航线或最小航时航线；也可以根据航次时间限制，选择满足航时要求的最少燃油航线。同时，还可以从图10中的Pareto航线解集中根据需求选择最优折中航线。求解得出的最小航时航线、最优折中航线、燃油占优航线（燃油0.7：航时0.3）和最少燃油航线的数值比较结果如表4和图11所示。

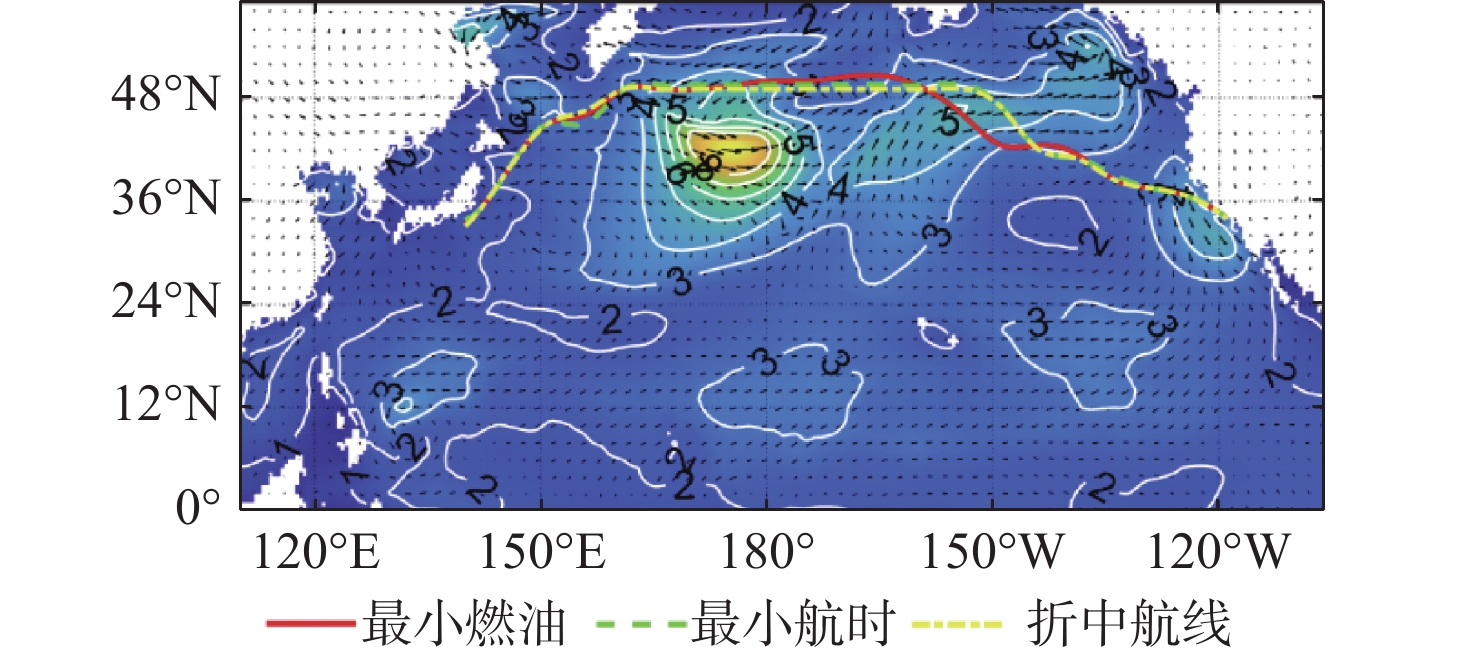
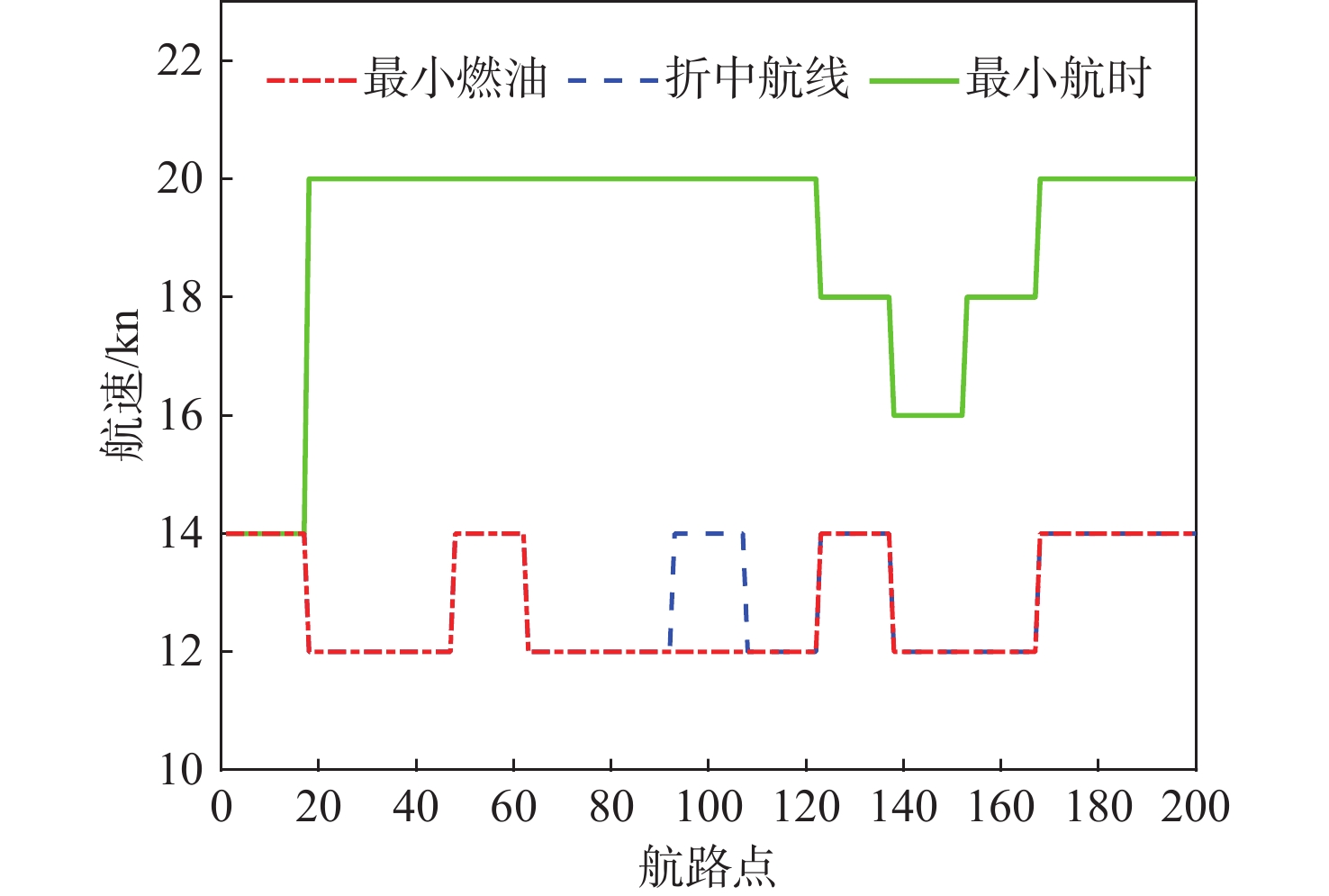
表  4  航线对比

Table  4.  Routes comparison list

序号	航线名称	航行时间/h	船舶油耗/t
Ⅰ	最小航时航线	281.308	1 899.48
Ⅱ	最优折中航线	349.648	1 097.79
Ⅲ	燃油占优航线	372.122	940.69
Ⅳ	最少燃油航线	407.072	776.97

下载: 导出CSV 

| 显示表格

图  11  航线数值比较

Figure  11.  Numerical value of the routes

下载: 全尺寸图片 幻灯片

图12为船舶航线可视化结果，图中白色等值线为等波高线，黑色箭头表示风速和风向，高亮区域是浪高大于6 m的危险区域。从图中可以看出，3条航线在前半部分均成功避开了大风浪区域，最小航时航线在后半部分更接近大圆航线，20 kn的航速占比较大，航行时间更短，符合航海实际情况；船舶在最小燃油航线上避开大风浪区域后，相较于最小航时航线，可更快地向低纬度地区航行，12 kn的航速占比更高，燃油消耗较少。折中航线与最小航时航线重合度较高，14 kn的航速占比更高。其中，各条航线的航速配置如图13所示。

图  12  航线对比图

Figure  12.  Route comparison map

下载: 全尺寸图片 幻灯片

图  13  船舶航线航速配置

Figure  13.  Ship route speed configuration

下载: 全尺寸图片 幻灯片

结合航线走势和航速配置分析结果可以看出，为了节省燃油和航时，各航线均避开了大风浪区域，且船舶航时及燃油消耗与航速的关系也符合船舶航行规律。

A*算法是目前求解气象航线和最优航线的主流精确算法之一。与单独使用A*算法相比，本文提出的结合A*与NSGA-II的多目标优化算法能在较短时间内生成包含多条最优航线的解集，供驾驶人员根据具体航次需求选择航线。两种算法的对比结果如表5所示。

表  5  算法对比

Table  5.  Comparison of two algorithms

算法	运算时间/min	优化航线数量
A*算法	15	1条
本文算法	10	多条

下载: 导出CSV 

| 显示表格

综上所述，本文提出的船舶航线多目标优化方法可适用于当前船舶航线设计和优化，对未来智能船舶的航行决策也具有一定的支撑作用。

4.   结　论

面向远洋船舶航线规划问题寻优空间大、航次任务目标复杂的特性，本文提出了一种结合启发式算法与精确算法的船舶多目标航线规划方法。该方法将A*算法引入NSGA-II中，通过引导搜索方向，加快算法收敛速度。该方法能够在较短时间内生成针对航时和油耗优化的最优航线Pareto前沿面，并可根据船舶自身约束和限制选择最适航线。

研究成果能够适应多变的远洋航行任务和需求，为船舶提供最优航线和航速配置，一定程度上解决了远洋船舶航线规划问题，可应用于我国气象导航系统及船舶智能航行系统。

下一步拟将季节性气候航线引入航线优化进程，引导航线搜索，进一步加快航线求解速度。